
"[...] l’ordinateur était et est resté un concept philosophique et mathématique prodigieux. S’il a modifié la société en tant qu’outil pratique - nous savons tous à quel point il a modifié nos vies - il est encore plus révolutionnaire en tant qu’idée. Pourquoi ? Parce qu’il transforme l’épistémologie et la signification même du mot comprendre.
Pour moi on ne comprend que ce que l’on est capable de programmer, et de programmer soi-même. Autrement on ne comprend pas vraiment, on croit seulement comprendre"
On peut ne pas partager complètement le ressenti de Grégory Chaïtin - métamathématicien visionnaire qui a révolutionné notre perception du hasard - sur l’évolution du mot comprendre, ne serait-ce que pour des raisons pratiques. Nous échangeons désormais nos scripts et nos programmes sur des plateformes dédiées, et nous apprenons ainsi tous largement des productions des autres. Nous apprenons, et comme professionnels de l’apprentissage, nous prenons à notre charge la question de la compréhension. Les multiples scripts ou programmes disponibles ici et là sont autant de réalisations mises à notre disposition pour précipiter cette compréhension.
Dans le domaine scolaire, la relation entre la compréhension et l’acte individuel de programmation est bien entendu d’actualité. On n’apprend pas le piano en allant au concert, ni le vélo en regardant le tour de France. S’exprimer, d’une façon ou d’une autre, dans le monde sensible nécessite un entrainement. Et si le résultat d’un programme est la dimension sensible de la programmation, celle-ci nécessite un entrainement et une structuration.
Note après la publication de la version 3.5
Cet article a été écrit en novembre 2009. Depuis avril 2010 et la version 3.5, les scripts peuvent être inclus dans la figure.
Tous les scripts de cet article - en particulier ceux de cette partie 2 sont disponible dans le nouveau format de classeurs de CaRMetal sur cette page qui contient plus de 50 scripts dont ceux de cet article
Présentation de la partie 2
C’est dans cette optique que nous poursuivons notre investigation, en abordant désormais l’interaction entre le monde sensible de notre environnement - le produit fini, la figure géométrique - et ses outils de productions plus virtuels que les outils géométriques usuels, la programmation, et plus précisément les variables JavaScript.
En fait l’interaction est très simplement régie par deux règles, que nous abordons au premier onglet, avec des applications au deuxième. Une déclinaison spécifique de la seconde règle a fait l’objet d’une syntaxe particulière que nous voyons au troisième onglet. Ceci acquis, c’est l’occasion de revenir sur le tableur pour approfondir, dans un cadre désormais géométrique, la réflexion déjà menée sur cet outil à plusieurs reprises dans la partie 1 dans un environnement seulement arithmétique. Le dossier se termine par des considérations - surprenantes - réservées aux curieux de la géométrie et/ou de la programmation.
Rappelons enfin que ce choix de rester dans un registre uniquement géométrique n’est pas du tout une limite du logiciel ou des CarScripts. D’autres collègues utilisent le même outil pour des statistiques en seconde comme sur ce topic du forum des Carscripts.
Les onglets de cette seconde partie
Calculs dynamiques : Les règles de l’interaction entre configuration dynamique et JavaScript.
Applications : Application fonctionnelle de ce qui précède.
Itér dyn : Nouvelle syntaxe à propos du contenu des variables JavaScript à envoyer à CaRMetal.
Tableur (2) : Retour sur la relation entre l’itération et le tableur dans leur dimension dynamique.Tous les onglets suivants contiennent des applets java, les pages peuvent être plus longues à charger.
Bool : Gestion logique à l’intérieur des coordonnées : compléments à l’attention des enseignants.
Tempo : Du temps dans les fils, en manipulation directe. Perspectives sur l’introduction du temps en géométrie dynamique.
Manips : Deux onglets avec les figures vues ci dessus en applet.
Nous précisons aux lecteurs qui arriveraient sur cette page sans avoir lu la première partie (détail sur les choix), que nous utilisons l’implémentation du JavaScript dans le logiciel de géométrie dynamique CaRMetal. Pour avoir une vue d’ensemble plus générale (non spécifiquement géométrique) mais aussi aborder des détails techniques voir ce TP de prise en main (pour enseignant), article avec applets et PDF associé. Dans un second temps on pourra se référer au manuel de référence disponible en fin de cette rubrique qui contient aussi les narrations de recherche de Alain Busser sur ses TP d’algorithmique en classe de seconde).
Calculs dynamiques
6. Interactions dans les scripts entre les variables et les objets géométriques
Nous abordons dans cet onglet une nouvelle dimension d’interaction entre le langage JavaScript et les figures CaRMetal : comment inserer une variable JavaScript - typiquement pour ce qui est d’une utilisation scolaire, une variable de boucle d’itération - dans une figure CaRMetal, c’est-à-dire dans une figure dynamique ? En pratique cette variable sera un pas de variation pour toute sorte d’objets, et en premier lieu pour le partage d’un segment, d’un cercle, etc ...
6.a. Description de la situation
La question peut surprendre : on a déjà spontanément insérer des variables JavaScript dans des figures, on peut même dire que nous n’avont fait que cela puisque, dans l’onglet précédent, toutes les figures construites par des scripts ont été faites à partir d’une feuille blanche. Nous avons même indicé des points avec une variable d’itération, et produit des figures dynamiques de cette façon.
Assurément, mais comment l’avons-nous fait ? De manière géométrique, en utilisant uniquement des fonctionnalités géométriques écrites pour étendre le JavaScript à la géométrie dynamique, procédé particulièrement pratique et efficace en particulier parce qu’il évite totalement la question de la relation au numérique. Car, comme on l’a vu en détail dans la construction de la spirale, donner une valeur numérique à un point dans un script, c’est initialiser un point libre, accessible à la manipulation directe. Ainsi, avec ce type d’utilisation numérique, on ne peut pas construire de relation géométrique - puisque tous les points sont libres. Concrêtement, on ne peut pas prendre de cette façon le tiers ou le dixième d’un segment [AB] qui resterait dynamique dans la manipulation du segment.
En fait la question initiale est formulée de manière maladroite car centrée sur la notion de variable, alors que celle-ci n’est qu’un outil. La vraie problèmatique est plutôt : comment réaliser dans un script un calcul qui soit dynamique, c’est-à-dire qui produise une figure dynamique ?
Réaliser un calcul, à partir de points d’une figure, demande d’avoir au minimum accés à leurs coordonnées, et à quelques fonctionnalités mathématiques de base. Si on pratique un peu en profondeur la géométrie dynamique, on sait que toutes ces fonctionnalités sont disponibles dans les logiciels. Par exemple dans CaRMetal on peut construire le centre de gravité par intersection des médianes mais aussi par les coordonnées :

Signalons à cette occasion, cette fonctionnalité de remplissage automatique quand l’icone de chainage est activée : on rentre une ligne en X elle est traduite en Y automatiquement.

CaRMetal dispose donc de la bibliothèque de fonctions mathématiques : x(M) et y(M) désignent les coordonnées de M, dans le repère interne au logiciel, on utilise classiquement sqrt pour la racine carrée, cos et sin s’appliquent à des angles en degrés, pour une utilisation au collège. On utlisera rcos et rsin pour des angles en radian.
D’une manière générale toutes les fonctions utilisables dans les coordonnées de points ou dans les expressions ou tout autre champ (comme les champs conditionnels) sont accessibles par un clic-droit sur le bouton bleu qui suit chaque item où elles peuvent être employées.
Plus généralement, mentionnons que le nom d’un segment est aussi une variable numérique qui représente la mesure de sa longueur, plus accessoirement, le nom d’un cercle est aussi une variables qui donne son rayon. Ainsi, pour un segment [OA], utiliser son nom, par exemple s1, ou sAB, remplacera avantageusement une expression comme sqrt((x(B)-x(A))^2+(y(B)-y(A))^2) dans une formule !!!!
Maintenant que nous avons vu comment CaRMetal rend accessible les informations numériques de ses objets, examinons comment on peut les utilser dans un script. On pourrait penser qu’il s’agit de faire coexister deux langages, celui du script, universellement répandu, et celui de CaRMetal qui ne fait que reprendre une syntaxe mathématique usuelle des logiciels. Mais ce point de vue, comme la première question de ce paragraphe, n’est peut-être pas très pertinent.
En fait, intégrer JavaScript à un logiciel de géométrie dynamique consiste à ajouter à JavaScript des nouvelles possibilités et de préciser les règles d’écriture de ces possibilités.
La seule façon d’étendre significativement JavaScript avec un typage minimal consiste à ajouter de nouvelles interprétations, géométriques, de chaînes de caractères. Toutes les fonctionnalités ajoutées au JavaScript (comme Point, Symetry etc) ont pour paramètre des chaînes de caractères, et renvoient une variable qui est une chaîne de caractère.
Ainsi quand on a écrit dans des scripts précédents une expression comme a=Point(0,-1), non seulement a est une chaîne de caractères, mais les deux nombres 0 et -1, de par le faible typage de JavaScript, sont acceptés comme chaînes et interprétés ensuite numériquement par la fonction/procédure Point.
De même, pour une écriture Point(0,2*i+1) dans une boucle, le nombre 2i+1 est calculé et envoyé, comme chaîne à la fonction Point qui l’interprète comme une donnée numérique.
6.b. Une première règle : le passage par chaîne de caractères
Pour transmettre une information non numérique à CaRMetal, il faut qu’elle soit explicitement dans une chaîne de caractères, entre guillemets.
Dans le script suivant, m et j sont les deux mêmes points. Le premier utilise les extensions géométriques prédéfinies, le second est défini à partir des coordonnées de A et B. Dans l’illustration de droite,on a déplacé A et B et on voit que les deux milieux sont bien dynamiques.

ou encore ici avec un isobarycentre dynamique, par script

Cherchons à construire, à partir d’un sommet A, un carré d’abord centré en l’origine du repère : une opportunité pour programmer un peu de la géométrie repérée, et l’occasion, pour l’orthogonalité, d’utiliser éventuellement :
Un changement de cadre possible
En seconde, si on ne connaît pas la relation entre les coefficients directeurs de deux droites orthogonales, ou si on n’arrive pas à faire le lien avec les coordonnées de l’extrémité d’un segment orthogonal à un autre, une autre voie peut être d’utiliser les relations trigonométriques cos(a+π/2) et sin(a+π/2) en fonction de cos(a) et sin(a) : elles donnent directement un segment de même longueur orthogonal au premier.

Selon le contexte de la classe, on peut poursuivre avec un carré de centre O de sommet A, ou le proposer pour un travail collectif avec validation au vidéoprojecteur. Il faudra alors utiliser que x(C)=2x(O)-x(A) et en déduire les coordonnées de B et C. La situation est bien moins simple pour les élèves, et c’est un vrai travail sur les coordonnées avec validation immédiate par l’application du script. Comme dans le script ci-dessous, on tracera les segments [OA] et [OB] pour vérifier l’orthogonalité. Le fait de prendre O en (0,0) initialement fait que beaucoup d’erreurs possibles paraissent « valides » dans le dessin produit. C’est un choix intéressant (surtout dans une utilisation collective) pour illustrer que l’on peut avoir plusieurs représentations fausses invalidées en déplaçant O pour voir ce qu’il en est dynamiquement.
En tant qu’exercices sur la géométrie repérée avec validation par la figure dynamique, ces premiers exemples ne relèvent pas à proprement parler des scripts. On aura bien compris que tout ce qui est entre guillemets peut directement s’écrire dans la fenêtre du logiciel en tapant les relations directement dans les coordonnées (et cela va plus vite car l’ordonnée est tapée automatiquement par rapport à l’abscisse).
Ces exercices, présentés dans l’interface de l’éditeur de scripts sont une première étape pour la prise en compte de l’interaction entre le JavaScript et les figures dynamiques. En effet, dans ces exemples, on ne travaille qu’avec les données numériques des objets de la figure, en les composant selon les besoins de la construction souhaitée. La question de l’interaction avec une variable JavaScript n’est toujours pas abordée. Et puisque l’on travaille l’itération, il reste à savoir comment utiliser au minimum une variable d’itération dans une coordonnée de point.
6.c Une deuxième règle : le passage par contenu des variables JavaScript
En effet, on ne passe dans les chaînes de caractères que des expressions construites à partir des données de la figure, ce que ne sont pas, a priori, les variables d’un script. On ne transmet pas une variable JavaScript à une figure CaRMetal directement, mais on transmet sa valeur. Le mot valeur est pris ici dans un sens informatique large de contenu, on préfèrera, pour éviter les confusions, parler de passage par contenu.
En classe comme les variables utilisées seront longtemps seulement à valeur numérique, même si cela va cristalliser une certaine représentation, on pourrait décider de faire le choix de parler de « passage par valeur ». Mais pour l’analogie suivante, le terme de contenu est préférable, car c’est vraiment de cela dont il s’agit.
En effet un paralléle avec le fonctionnement du tableur est saisissant. Une cellule du tableur n’est pas son contenu. En cliquant sur une cellule, c’est comme si on ouvrait la boite, on voit son contenu en particulier la formule qui donne la valeur numérique. De même une variable JavaScript n’est qu’un nom, l’étiquette d’une boite, et on passe à CaRMetal le contenu de cette boite.
Syntaxe : On note _k le contenu de la variable k.
Par exemple pour partager un segment en 7 parties, il suffit d’utiliser dans une boucle la syntaxe suivante (points manipulés ensuite pour vérifier que les points sont bien construits à partir de A et B) :

ce qui peut se vérifier aussi par un clic droit sur ces points pour voir leurs coordonnées, elles ne sont plus numériques mais bien algébriques et le coefficient i de la boucle est passé par son contenu, la valeur numérique 4 :

Enrichissons un peu tout ceci avec un nombre de division donné en paramètre par l’utilisation et deux segments à partager pour faire un tableau de fil comme vu de manière statique à la fin de l’onglet sur la console.
Le script s’arrete à la demande du pas, on voit les trois points de base et les deux segments construits

Puis la figure construite est manipulable, le tableau de fil est affine et dynamique :
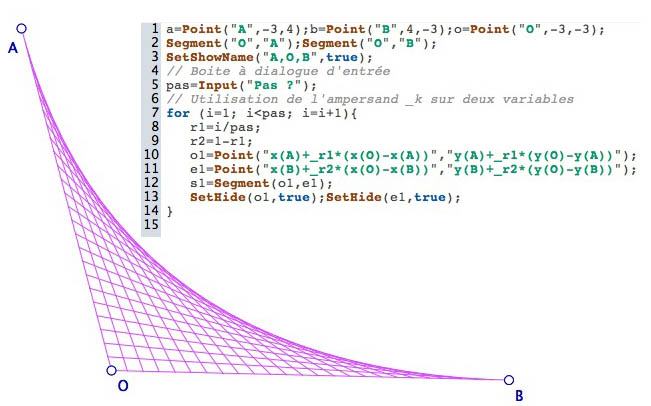
On remarquera qu’à part la syntaque du tiret souligné, comme _r pour utiliser une variable r, le reste de l’écriture des coordonnées est particulièrement proche de l’écriture mathématique traditionnelle, et largement uilisable en classe, surtout dans un contexte de travail de géométrie repérée.
On peut alors facilement, sans autre connaissance que ce qui vient d’être vu, par de simples copier-coller et ajustement de noms de points, produire rapidement ce genre de figure dynamique :

6.d. Application à un cercle
L’étape suivante pourrait être de partager un cercle au lieu d’un segment. On a parlé dans un précédent onglet de la possibilité d’utiliser le nom du segment [OA] pour désigner la longueur OA. On peut proposer ce script à analyser et commenter (c’est une des compétences attendues) comme script générique, prélude à de vraies figures.

On notera que les points du cercles ainsi obtenus on des angles « absolus » sur le cercles : il y a de fait une référence à une origine implicite sur l’axe,qui correspond au cercle trigonométrique. En conséquence les points construits ne tournent pas avec le point A quand on agit sur A. Dans des activités de seconde on peut ne pas aborder cette question tant qu’elle n’est pas soulevée par un élève ... d’autant que les deux figures suivantes font largement illusion.
Sur un plan technique, à l’attention des enseignants, on notera que la construction de s1, si elle est naturelle est intuitive en classe, est en fait inutile. On aurait tout aussi bien pu mettre co à la place de s1 pour avoir le rayon du cercle puisque, comme nous l’avons déjà souligné, le nom d’un cercle est aussi une variable qui représente son rayon. Mais c’est plus ésotérique pour l’écriture, et didactiquement il est préférable d’en rester au segment.
Il faut alors peu de chose pour modifier ce premier script en un limaçon de Pascal, ajouter simplement un cercle à tracer au lieu d’un point :
On notera l’utilisation fonctionnelle du point plutôt que procédurale, pour avoir une variable de sortie, ce qui permet de construire les cercles sans avoir à écrire une écriture indexée des noms de points de type « A »+i comme on a pu le faire dans la partie précédente.
Bien entendu la construction est dynamique, on peut déplacer le point M, placé un peu par malice initialement sur le cercle, d’abord pour demander aux élèves pourquoi le point bleu est sur le cercle, mais aussi illustrer le fait qu’il est toujours facile de produire des cas particuliers. Le point A ne sert qu’à modifier le rayon du cercle. D’où l’illusion mentionnée ci-dessus.
On peut poursuivre en ajoutant quelques lignes :

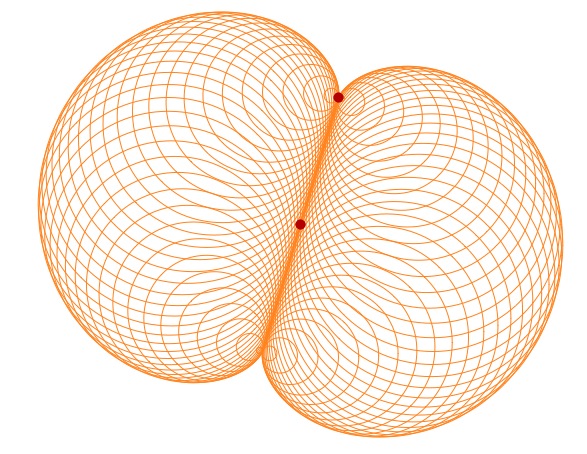
Chacun aura noté qu’au lieu de diviser i par n pour passer le quotient par contenu comme fait dans le limaçon, on a mis i et n dans les coordonnées des points. Bien entendu, c’est à la fois une complexité d’écriture et une perte d’efficacité puisque l’on fait une même division deux fois. Et donc, si on rencontre cela en classe, c’est l’occasion de parler, même brièvement, d’efficacité des programmes.
On peut attacher le point A sur un cercle de centre O et faire une animation sur A comme déjà décrit plus haut.
6.e. Utiliser d’autres variables de la figure
Au lieu de tracer des cercles on peut tracer des segments. On sait qu’on construit une cardioide par enveloppe des segments reliant les points d’indice i et 2i :
Mais sur cette figure on peut avoir envie de pouvoir faire tourner le point A sur le cercle. Là on voit bien que l’on n’a qu’un dessin statique, on aimereait lui ajouter la possibilité de manipuler un point du cercle préalablement constrit.
La figure est proposée à l’attention des enseignants, pour explorer la possibilité dégagée. Elle ne s’inscrit pas dans une logique de progression en classe. Mais elle serait abordable en 1°S, à propos d’un travail sur les angles.
En pratique, on ne peut pas placer un point sur objet en script. C’est un oubli probablement, car on peut placer un point aimanté, ce qui est suffisant. Mais un point aimanté ne peut être animé automatiquement or c’est ce qu’on a envie de faire bien entendu. Il en résulte que nous allons appliquer un script sur une figure préconstruite : un cercle, un point A sur ce cercle (et qui ne définit pas le cercle), un segment et un angle. Cette figure PourCardioideDyn est téléchargeable en fin d’article.
Applications
7. Utilisation d’une fonction
Dans notre séquence d’apprentissage de l’itération dans un environnement de géométrie repérée, nous abordons la dernière phase avec cet onglet, que nous pourrions intituler onglet de la créativité.
En effet, il y a au minimum un invariant dans cette science de la programmation, c’est la satisfaction du résultat. Qu’il soit expert international au CERN ou élève de seconde, chaque (apprenti) algorithmicien, chaque programmeur est heureux d’arriver à mettre en œuvre concrètement son algorithme et valider qui fait bien ce qui était prévu.
Nous savons désormais construire un carré, que ce soit géométriquement (5.1) ou algébriquement (6.a). Il ne va pas être difficile de construire un octogone ou un hexagone géométriquement. Nous savons aussi construire un tableau de fils à partir de trois points, de manière dynamique, nous abordons maintenant une systématisation de cela pour explorer des possibilités de dessins géométriques dynamiques. Pour cela nous allons structurer nos programmes en trois phases
– Phase 1 : préparation de la figure initiale et demande d’un pas.
– Phase 2 : mise en place d’une procédure générique de tracés de fils (la même pour tous les programmes).
– Phase 3 : choix des différents appels de la fonction de tracé de fils.
Pour la première phase, il suffit de copier coller des constructions initiales d’un carré, pentagone, hexagone, octogone. La phase 2 va être précisée dessous, en ensuite chacun peut explorer les possibilités de la phase 3.
7.1.a. Les constructions initiales
D’une manière générale, travaillant avec un polygone régulier, on travaille implicitement ou explicitement sur un cercle. Le plus simple est de partir d’un point O centre du cercle et d’un point A tel que OA soit le rayon du cercle circonscrit au polygone. Même si on a besoin de construire le cercle de centre O passant par A pour les besoins de la figure, on peut le cacher et ultérieurement. La figure terminée avec le Carscript, on pourra ensuite attacher A à un autre cercle de centre O pour lui appliquer une animation (c’est ce qui est fait dans les exemples des onglets suivants).
Voici un script qui reprend les différentes constructions, que l’on peut copier et adapter.
Le plus complexe est celui du pentagone. Il peut être donné aux élèves. Dans le cadre d’un travail hors temps scolaire, de type « club et/ou exposition », on peut bien entendu laisser les élèves chercher la construction sur le net et la transcrire en programme de construction. (Ci-dessous le pentagone a été recolorisé aprés le script)

7.b. La fonction générique centrale
Le travail de tableau de fils dynamiques proposé dans l’onglet précédent (6.c) peut être systématisé, un peu comme le ferait une macro-construction.
Mais l’avantage de conserver les scripts est de garder le nombre de divisions choisi à chaque lancer du script par l’utilisateur : cela permet à des élèves de commencer par un petit nombre pour tester leur figure puis de prendre un grand nombre pour des versions finales à imprimer par exemple.
La boucle principale du tracé de fils, que l’on a recopié 7 fois dans un script précédent se transforme tout simplement en une fonction qui peut être de cette forme :

Note technique de seconde lecture
Les programmeurs seront surpris de la recopie des paramètres transmis dans la fonction : c’est la seule condition à remplir pour que l’interfaçage entre le JavaScript et les constructions dans CaRMetal fonctionnent à l’intérieur d’une fonction JavaScript. On notera qu’il n’est pas nécesssaire de recopier col - comme c’est fait ci-dessus - car cette variable ne s’applique pas dans une chaîne de caractère mais seulement à une fonctino JavaScript. Le passage par paramètre est alors standard.
Cette fonction est ensuite simplement appellée plusieurs fois en fonction de ce que l’on veut faire, comme par exemple ci dessous à partir d’un pentagone :
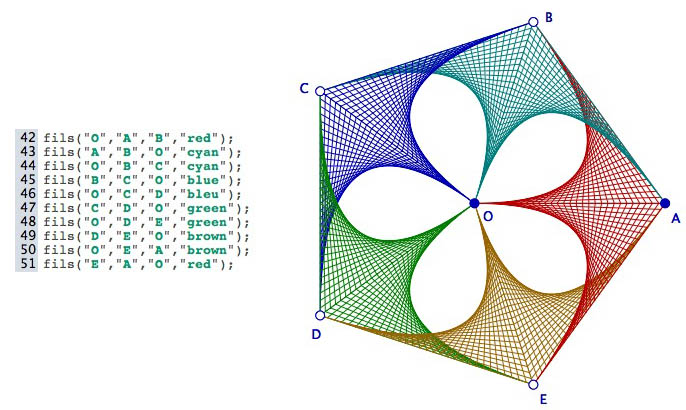
7.c. Quelques exemples d’utilisation
On peut remarquer que l’utilisation des fonctions n’est pas explicitement au programme, mais on peut entendre cela comme une précision de ne pas complexifier les programmes avec des fonctions ou procédures mathématiques complexes.
On voit que dans un contexte graphique, une fonction de tracé, loin de rajouter à la complexité, nous libère de la tâche du tracé effectif pour nous recentrer vers une production de figures (ou « dessins dynamiques » puisque, travaillant sur des figures régulières, il y a peu de paramètres accessibles à la manipulation directe).
Cette simplification apparente permet d’aborder d’autres questionnements comme par exemple :
– Respecter un ordre de construction dans le script (continuité du mouvement des segments)
– Décompte du nombre de segments et de points construits.
Le premier est intéressant à mettre en oeuvre car il permet de travailler sur l’orientation et son lien avec la programmation. Le second point fera observer - et on peut le vérifier avec le logiciel, le doublement de beaucoup de points. Alors, selon le contexte (en particulier dans des activités hors temps scolaire), cette réflexion pourrait aboutir à des écritures légèrement plus optimisées du tracés. Par exemple on pourrait décider, pour des tracés comme ci-dessus, d’avoir une fonction spécifique pour l’utilisation des rayons ([OA], [OB]) : ces procédures, utiliseraient 4 points ne construiraient qu’une seule fois les points sur les rayons.
De nombreuses variantes sont possibles. Voici quelques illustrations.
Avec un carré
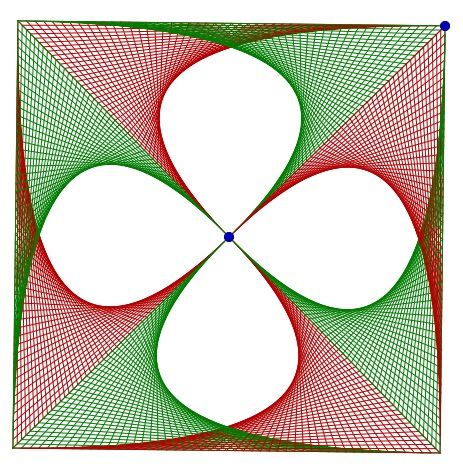
Avec un hexagone (configuration naturellement plus prisée)
Autre construction sur l’hexagone
On peut reprendre les mêmes constructions et de nombreuses variantes avec un pentagone, ou un octogone.
7.d. Prolongement
Toujours dans le cadre d’un travail hors temps scolaire, on peut jouer sur les couleurs et incorporter trois paramètres Rouge,Vert,Bleu en utilisant le SetRGBcolor dans la fonction.
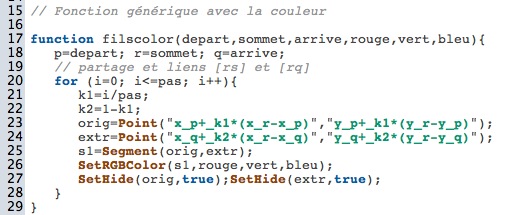
on note qu’il n’y a pas à recopier les paramètres de couleur car ils sont seulement utilisés par une fonction générique, mais non manipulés dans une chaîne de caractères.
Ce qui donne par exemple
Un exemple avec un octogone
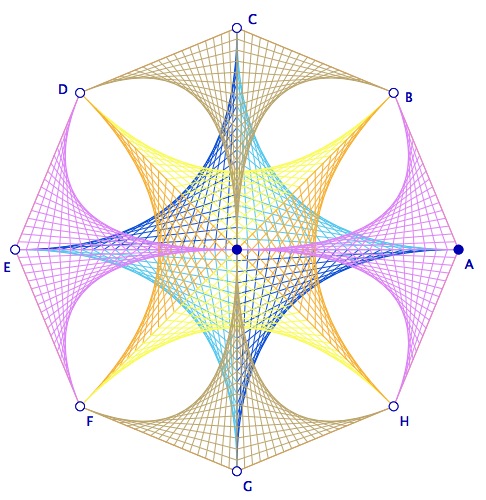
On peut aussi, comme dans les illustratons du 6.e, ne pas mettre de référence aux couleurs et jouer avec la palette de couleurs du logiciel.
7.e. Exportation grand format
Dans le cadre d’une exposition de productions d’élèves, rappelons que l’on peut choisir l’épaisseur des traits dans la palette d’outils, et qu’il est possible de tripler les longueurs et largeurs dans l’exportation en PNG.
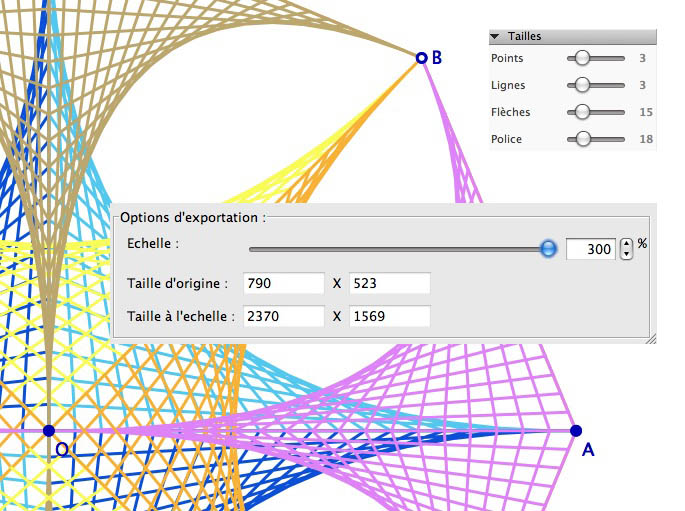
Ceci permet de produire une bonne sortie A3, que l’on peut photocopier en A2 selon les besoins, et les possibilités matérielles.
Iter Dyn
8. Itération dynamique - Utilisation d’un contenu plus complexe des variables
Dans les constructions précédentes, utilisant des figures régulières, nous sommes sur ce que nous avons appelés des dessins dynamiques car si la figure finale est bien en manipulation directe, elle dépend de peu de paramètres, essentiellement d’un point que l’on peut placer sur un cercle par exemple.
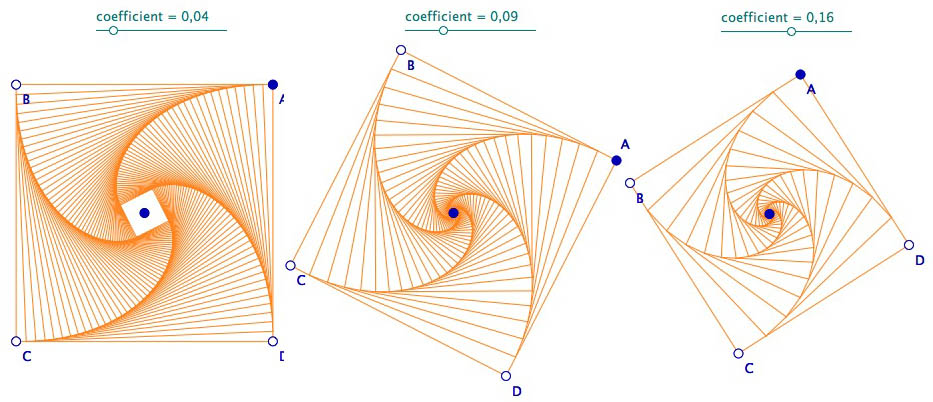
Nous nous proposons de revenir à des figures plus dynamiques, en mettant un paramètre de réduction sur des constructions comme celles vue en 5.1. Dans cette partie nous avions eu explicitement une approche géométrique, en prenant d’abord les milieux, puis les milieux des milieux. Ceci, bien entendu pour éviter tout recours aux coordonnées. Cette fois-ci, même s’il s’agit de similitudes, et donc de transformations géométriques, pour une utilisation plus large, accessible à beaucoup plsu de classes, nous choisissons le registre de la géométrie repérée - de toute façon beaucoup plus simple. Pour cela nous allons utiliser un paramètre qui permet de choisir la position d’un point sur le segment [AB] pour engager l’itération comme illustré ici :
Ceci ne pose pas de problème, nous savons prendre une division d’un segment. Et si celle-ci est donnée à partir d’une variable de la figure, c’est encore plus simple qu’avec une variable JavaScript.
Rappel : Pour construire le curseur coefficient, on prend l’icone d’expression comme ci-dessous avec les paramètres indiqué, en respectant le nom coef du curseur pour la suite.

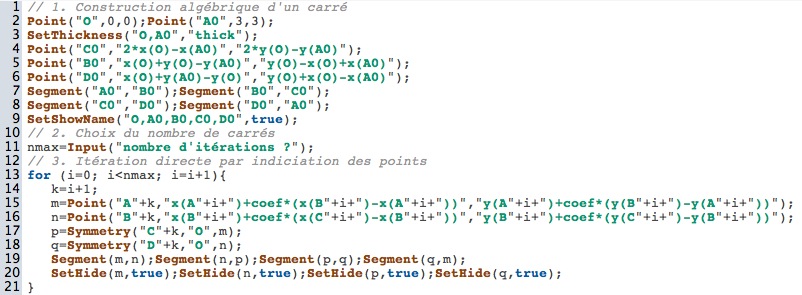
Toute la figure dépend de ce paramètre. Il nous faut transformer le script déjà vu en 5.1 dont voici en extrait, en remplaçant les données géométriques par des coordonnées :
for (i=0; i<10; i=i+1){
p=MidPoint(a,b);q=MidPoint(c,b);
r=MidPoint(c,d);s=MidPoint(a,d);
SetHide(p,true);SetHide(q,true);SetHide(r,true);SetHide(s,true);
Segment(p,q); Segment(r,q); Segment(r,s); Segment(p,s);
a=p;b=q;c=r;d=s;8.a La syntaxe x(_m) et x_m
On a vu la nécessité d’utiliser les variables JavaScript pour que le carré nouvellement construit (ci dessus pqrs) devienne le carré initial de la prochaine itération (abcd). Nous savons passer par contenu _k un indice de boucle k au sein d’une chaîne de caractères transmise à CaRMetal, mais comment passer l’abcisse d’une variable JavaScript a ? Nous ne l’avons encore jamais fait !
Faut-il utiliser x(_a) en prenant l’abscisse du contenu de a ? Effectivement c’est ce qu’il faut faire. Et parce que cette utilisation revient trés souvent dans les scripts, l’auteur du logiciel propose un raccourci que l’on peut aussi utiliser : au lieu d’écrire x(_a) et y(_a) pour indiquer l’abscisse et l’ordonnée d’une variable JavaScript de type point, on peut utiliser la syntaxe simplifiée x_a et y_a, sans les parenthèses.
Ainsi, aprés avoir placé un curseur dans la figure blanche, du nom de coef, on peut appliquer un script qui commencer par la construction d’un carré (comme dans l’onglet précédent) et poursuivre par :

<br clear=all
Nous avions vu en 5.1 les différentes étapes pour arriver à l’écriture de la dernière ligne du script. Si on n’a pas fait l’activité 5.1 et que l’on souhaite proposer celle-ci, il faut prévoir une ingénièrie pour y arriver. En pratique on fait une ou deux itérations manuellement (en consommant beaucoup de noms de variables) puis on se pose la question de l’itération. Conceptuellement c’est plus difficile car il s’agir de l’écriture itérative d’une démarche récursive. Nosu avions parlé en 5.1 de l’écriture de i=i+1 qui, pour dire l’itération, est récursive ...
8.b Une version par indiciation des points
On a vu, en 5.2 à l’occasion de la spirale, l’idée d’utiliser la variable de la boucle d’itération pour indicer les points utilisés. La démarche était assez élémentaire. On peut envisager de reprendre la même méthode pour éviter le passage d’un carré à l’autre, en calculant directement les coordonnées des sommets du carré d’indice k en fonction de ceux d’indice k-1. Pour cela on construit le carré initial avec l’indice 0.
En fait cette méthode, si elle présente l’avantage de construire directement les sommets du carré d’indice k, n’est pas trés lisible, et donc certainement moins simple à écrire pour un élèves. Elle est donnée ici pour la "culture de la chaîne de caractère" ;-). Mais elle reste sans intérêt pour une utilisation en classe, car uniquement centrée sur une utilisation technique des chaînes, sans la portée cognitive contenue dans l’autre méthode.
En contre partie de cette technicité, on a une maîtrise complète des noms des points créées comme on le voit ici en faisant apparaître le point B15 :

<br clear=all
8.c. Autres exemples
En conservant le principe de la boucle du script "standard" et en commençant par un hexagone, on arrive rapidement à ces figures (ici avec 120 hexagones) :
<br clear=all
Bilan de l’onglet
Dans cette partie, nous avons appris l’utilisation de la syntaxe x_m (pour x(_m)) qui permet de passer à CaRMetal un contenu (ici l’abscisse) d’une variable JavaScript plus complexe qu’un indice d’itération.
Nous avons vu comment l’utiliser dans une construction de figure très proche de la récursivité (transformation autoréférente).
Même si elle n’est pas très pertinente, nous avons aussi détaillé comment réaliser une construction plus itérative, en indiçant les noms des points construits et en écrivant une récurrence sur ces noms.
Tableurs (2)
9. Tableur en production géométrique
Avant d’aller plus loin - dans les onglets suivants, - vers une utilisation plus orientée vers la formation des ensiegnants, nous abordons dans cet onglet une dernière remarque autour de la réalisation dynamique de certaines figures avec un tableur. Pour illustrer notre propos, nous reprenons - rapidement - la construction du cœur du tournesol, largement plus commentée dans l’onglet du même nom de cet article.
Nous étions partis d’une figure avec un curseur nommé ang qui allait de 135 à 140 degrés. Puis nous lui avons appliqué ce script :

pour obtenir cette figure
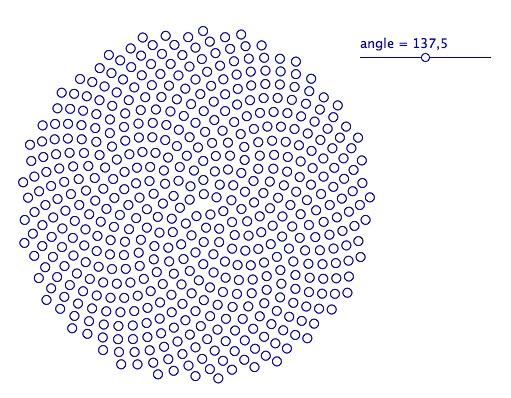
Ce script est constitué essentiellement d’une boucle d’une seule instruction Point.
Or, on peut faire exactement la même chose avec un tableur. Ci dessous - en copie d’écran, le fichier est téléchargeable en fin d’article - nous avons un curseur pour l’angle dynamique, un paramètre c comme dans le script, pour l’échelle. Bien entendu, la boucle est déclinée en lignes, et chaque partie de la ligne d’instruction du script est associée à une colonne.
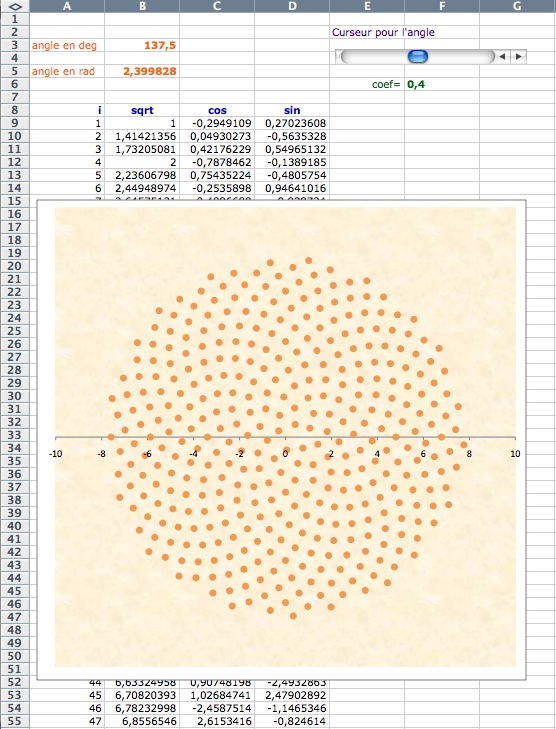
On voit que, pour peu que l’on connaisse les deux environnements, on fait rapidement une figure dynamique, manipulable avec un curseur, que ce soit dans la feuille d’un tableur ou en script de CaRMetal.
Et la comparaison, en formation, éventuellement en 1° ou Terminale, lors d’un travail sur les coordonnées polaires, est intéressante. Selon le point de vue que l’on veut illustrer, on peut voir aussi bien l’efficacité de l’algébrisation et de la boucle d’itération, que le prix à payer, en terme d’encombrement de calculs intermédiaires de la non algébrisation.
Pourtant la différence est minime : dans les deux cas, c est une constante, l’angle ang est un paramètre sous forme de curseur. La différence prinicpale entre les deux est dans le traitement de la seule variable de la situation, l’indice de la boucle. Dans le tableur la variation de la boucle est obtenue par une itération régulière à la poignée de recopie : la variation est construite par un geste à la souris : on fait le geste de la variation, en maîtrisant son étendue. Dans le contexte de l’analyse de la première partie de cet article, avec la mise en évidence de cette nécessité d’un travail préalable sur les objets à l’école primaire, on remarquera qu’il s’agit à nouveau d’une objectivation, cette fois du concept de variable, dans la mesure où l’on agit, physiquement, sur la feuille de calcul pour activer et piloter les valeurs que va prendre cette variable. Par ailleurs, l’action étant effectuée, on retourne dans le champ arithmétique de la table produite par le tableur.
En terme de changement de cadre, cet exemple illustre bien les différents sens que peuvent prendre les variables qui s’écrivent toutes algébriquement de la même façon, que ce soit la constante c, l’angle entre deux points du tournesol vus de son centre, ou l’indice de la boucle d’itération. Il n’aurait pas du tout été opportun de construire une feuille avec l’angle en variation dans des lignes alors que c’est lui que l’on active dynamiquement ... parce que ce n’est qu’un paramètre de la figure.
En formation ce type de changement de cadre illustre bien la difficulté que peuvent rencontrer les élèves sur l’algébrisation et comment le tableur permet de mieux préciser les enjeux, par accompagnement de la prise en charge des variables. On comprend aussi pourquoi dans les domaines non spécifiquement scientifiques, on travaille plutôt sur tableur pour faire les simulations, même largement paramétrées, plutôt que sur un CAS comme Maple ou Mathematica.
Bool
10. Ajouter une dimension booléenne aux tracés
Nous quittons, dans cet onglet et le suivant, le cadre scolaire pour aborder d’autres possibilités des Carscripts. Dans cet onglet, nous explorons la possibilité de placer un booléen dans une instruction JavaScript à destination de CaRMetal.
Si les figures suivantes ne sont que des exemples élémentaires construits autour des considérations précédentes (tableaux de fils), la méthode est générale.
Nous considérons un curseur système qui va prendre trois valeurs possibles 1, 2 et 3. Il se nommera ch. Pour cela on prend l’outil curseur dans l’item controles de la palette d’outils :

Puis on lui applique les réglages pour que le curseur soit un entier
On se propose de construire un tableau de fils, dont l’orientation des fils va être fonction de la valeur du curseur ch. En pratique - juste pour être rapide - comme la fonction de tracé des tableaux de fils utilise trois points, nous allons simplement faire une permutation circulaire sur ces trois points. Pour voir ce que cela donne, la figure est téléchargée en applet dans cet onglet.
Voici la modification pricipale du script (à explorer en attendant le chargement de la figure)
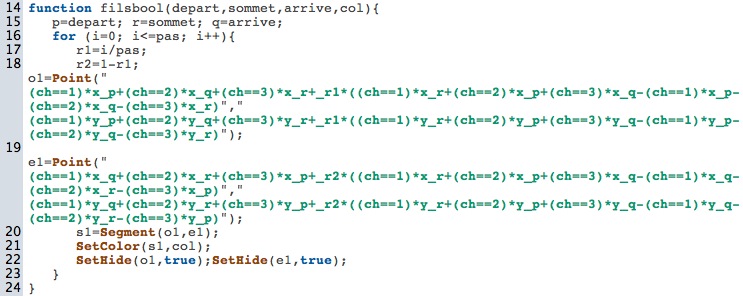
On comprend bien que l’utilisation est assez élémentaire, mais le résultat reste saisissant en terme de perspectives d’utilisation des booléens dans des scripts.
En particulier on voit clairement qu’il ne s’agit pas de construire trois types de segments et de les cacher/montrer selon les valeurs de ch, c’est bien un seul segment qui est construit, par script, dont les extrémitées varient selon ch.
La figure en manipulation directe
<carmetal|doc=2477|largeur=703|hauteur=543>
A partir du script précédent, chacun peut s’entraîner à produire quelque chose d’un peu plus esthétique, par exemple sur les carrés ou les octogones. Merci de penser alors à placer vos scripts sur les forums de CaRMetal par exemple à la suite de ce post.
Polygones booléens étoilés (164 Ko)
Une autre façon d’utiliser les booleéens dans les polygones est dans un traitement en amont : on va appliquer un script standard à une figure traitée de manière logique. C’est par exemple une façon élégante d’aborder l’itération des polygones étoilés : on construit les points du polygone sur les points souhaités en fonction du booléen,ou plus généralement du curseur, de polygone étoilé. Par exemple pour le pentagone, on peut partir d’un polygone régulier initial A, P, Q, R, S puis construire les points B, C, D, E sur P, Q, R, S, de cette façon :
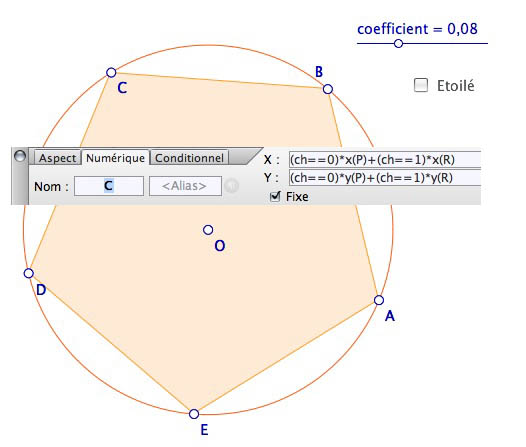
Sur la figure ainsi préparée (téléchargeable en fin d’article), on applique ce script ordinaire :
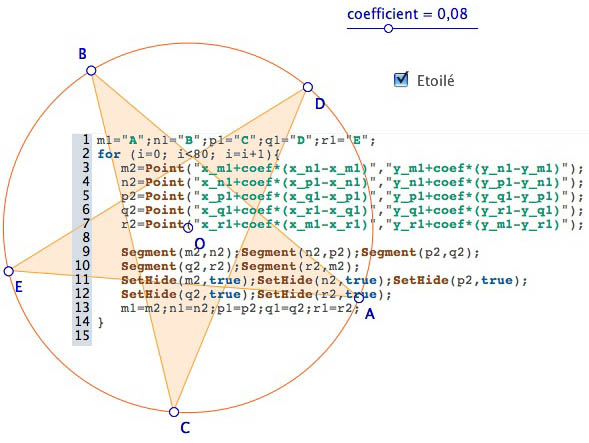
on obtient alors cette figure :
<carmetal|doc=2430|largeur=709|hauteur=503>
On étendra le procédé à d’autres types de figures booléennes. Merci de proposer vos scripts. En particulier, toujours sur ce post, on trouvera l’heptagone étoilé avec trois possibilités : régulier, étoilé1 et étoilé2, par le carré ou le cube de la première racine septième de l’unité.
Tempo
11. Exemple d’introduction du temps dans une itération
Nous poursuivons l’exploration de l’itération dans un contexte hors du champ scolaire, en l’interfaçant ici, pour la culture de la géométrie dynamique, avec une spécificité bien particulière du logiciel. Nous abordons là un domaine tout à fait remarquable sur lequel nous invitons le lecteur à se pencher avec curiosité.
11.a Rappel du contexte
Par principe, les logiciels de géométrie dynamique sont déterministes au sens où, quand les objets de base d’une figure reviennent à leurs conditions initiales, toute la figure revient à sa condition initiale. C’est une nécessité didactique qui a provoqué un cahier des charges très contraint, et qui fut difficile à respecter dans la gestion des intersections au début de la géométrie dynamique. Désormais tous les logiciels ont le comportement attendu sur les objets de base. Et tous, ont choisi cette voie (pendant quelques années, Cinderella a exploré une autre voie).
Il en résulte que les figures en géométrie dynamique sont toujours « au présent », elles ne peuvent contenir en particulier aucune trace de l’histoire de la manipulation de la figure par l’utilisateur. Et parfois nous en aurions besoin, en particulier pour les fonctions trigonométriques en lien avec la rotation d’un point sur un cercle, pour, au minimum, compter le nombre de tours.
CaRMetal est le seul logiciel de géométrie dynamique qui permet de faire cela, comme l’a découvert Eric Hakenholz dés 2005 sur CaR, propriété qu’il a implémenté ensuite avec une macro standard « curseur circulaire » dans CaRMetal depuis quelques années. Dans CaRMetal nous pouvons ainsi incorporer dans le comportement de la figure des traces de la manipulation par l’utilisateur, autrement dit assujettir la figure à l’histoire de sa manipulation, et donc incorporer du temps. C’est bien entendu une rupture du contrat initial du déterminisme des figures.
Il en résulte que, conceptuellement, la géométrie dynamique avec CaRMetal a donc un degré de liberté et une pertinence de simulation significativement différente des autres logiciels.
Sur le site de l’IREM de La Réunion, nous avons consacré un article à cette question : uniformisation du cercle. Il y a dans CaRMetal, deux autres façons de s’affranchir du déterminisme, une première avec la référence circulaire, présentée ici, une seconde avec l’aimantation, utilisée ici. La rencontre de l’aimantation et de la temporalité permet des simulations tout à fait extraordinaires comme décrites brièvement ici et là.
11.b. Cardioïde temporelle discrète
Nous allons utiliser la première temporalité, celle de l’uniformisation du cercle, et l’intégrer à un script tout simple celui de la cardioïde « dynamique » déjà construite.
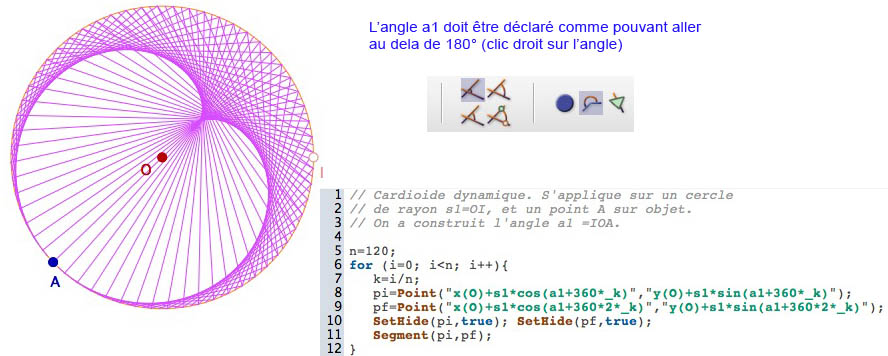
Voici donc une première figure qui part d’un curseur circulaire, de la macro du même nom (dans le dossier « pour expert » des macros de la bibliothèque), et qui construit une cardioïde, par script à partir de ces données. La figure initiale est téléchargeable pour y appliquer le script (en particulier pour une présentatino en formation).
Voici la figure et l’action à effectuer dessus
<carmetal|doc=2414|largeur=649|hauteur=493>
Ainsi que le script utilisé pour la construire (on a simplement ajouté le tour au rayon du cercle sA)
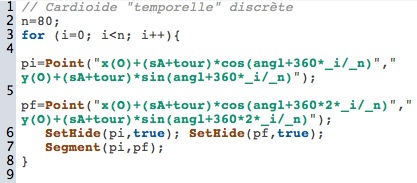
11.c. La cardioïde temporelle continue
Ayant vu que cela fonctionnait, on peut avoir envie d’y ajouter une variation désormais continue. Il suffit de prendre en compte le ratio d’angle au dela d’un tour et de le rajouter - rapporté à un tour - au rayon du cercle. (S’applique à la deuxième figure « PourCardioideTemporelle »).
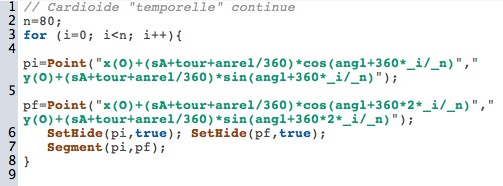
Ce qui donne la figure suivante
<carmetal|doc=2415|largeur=741|hauteur=493>
11.d. Bilan de l’onglet
Dans cet onglet, nous avons vu que CaRMetal permet d’inclure du temps dans les figures de géométrie dynamique - qui elles sont a priori toujours au présent. Puis nous avons vu que l’implémentation du JavaScript permet de traiter ces figures avec des scripts le plus naturellement possible, ce qui augure de belle possibilités de figures en physique par exemple.
Pour information, signalons que la possibilité de rompre le déterminisme des logiciels de géométrie dynamique, en utilisant des objets autoréférents, peut-être utilisé systématiquement - même sur des expressions - pour simuler des expériences de statistiques avec un seul objet lancé plusieurs miliers de fois : exemple des aiguilles de Buffon.
Manip1
12. Spirales et autres courbes
Voici, en applet java, deux figures sur les spirales et une sur la néphroïde, en manipulation directe
12.a. La spirale de demi-cercles (parties 5.2 et 5.3)
<carmetal|doc=2419|largeur=698|hauteur=512>
12.b. La spirale d’archimède
<carmetal|doc=2420|largeur=790|hauteur=523>
12.c. Néphroïde avec curseur
Nous avons déjà construit la néphroïde. Ici on a ajouté un curseur pour le nombre de cercles. Si l’essentiel de la figure est faite avec une variante du script vu dans ces pages, pour le moment la finition - que chacun imaginera - ne peux pas être entièrement réalisée en script. Elle a donc été faite manuellement.
<carmetal|doc=2421|largeur=790|hauteur=523>
Manip2
13. Deux figures d’itération
13.a. 100 itérations du carré
Figure de 400 segments (148 Ko)
<carmetal|doc=2423|largeur=790|hauteur=523>
13.b. 100 itérations de l’hexagone
Figure de 600 segments (240 Ko)
<carmetal|doc=2422|largeur=726|hauteur=497>
Fun
14. Un mélange des genres
Même si cela ne sert à rien, un mélange de booléen et de début d’itération
Figure de 360 segments seulement, mais de 584 Ko, donc longue à charger.
<carmetal|doc=2476|largeur=699|hauteur=644>
La figure est obtenue à partir du script suivant, sur une figure qui contient deux curseurs : ch, qui va de 1 à 3 par pas de 1, et coef qui va de 0 à 1 de manière continue.
Forum sur les Carscripts | dont Statistiques en seconde | Télécharger CaRMetal





Commentaires