Voici une approche algorithmique de ce célèbre problème :

Pour limiter le nombre de filles dans un pays, on décide que :

• chaque famille aura au maximum 5 enfants ;
• chaque famille arrêtera de procréer après la naissance d’un garçon.

Question : Est-ce que ça marche ?

Comme la variable bébé est un tableau contenant les deux mots « garçon » et « fille », on peut simuler une naissance par bébé auHasard. Simuler une fratrie est plus compliqué : On initialise la fratrie à une collection vide, puis on y ajoute un bébé au hasard tant qu’aucune de ces conditions n’est réalisée :

• la naissance du 5^e bébé : On arrête les frais
• la naissance du premier garçon :

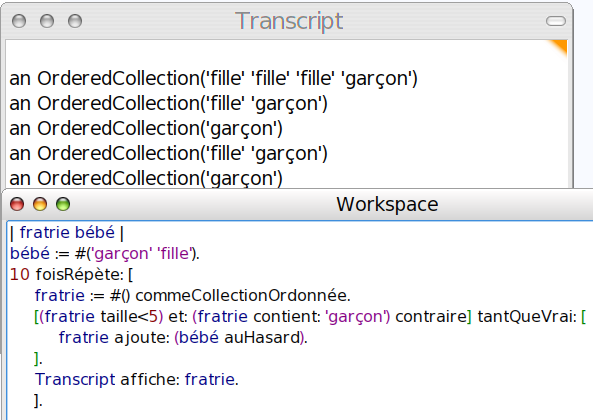
Pour faire une étude statistique, il suffit de simuler 10000 fratries [1] et de les fondre en entier dans une population initialement vide :

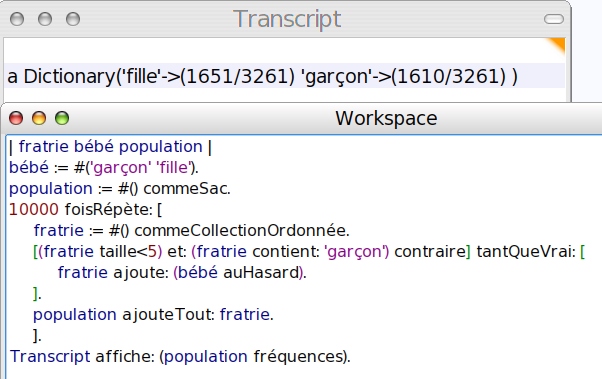
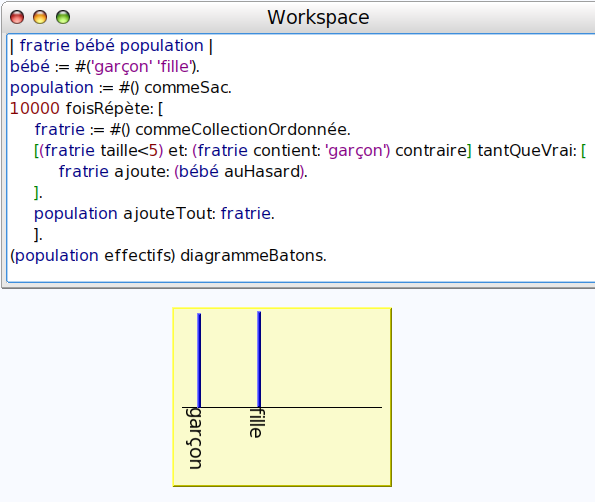
1651 filles pour 1610 garçons : La politique nataliste de ce pays est en échec. La confirmation visuelle se fait avec le diagramme en bâtons :

Testé dans une classe de 27 élèves :

Quelle est la probabilité que deux d’entre vous aient leur anniversaire le même jour ?

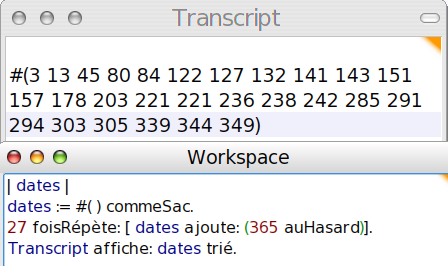
Une façon simple de simuler le problème est de prendre une liste de 27 nombres choisis au hasard entre 1 et 365 :

Seulement il est difficile de voir si un nombre apparaît deux fois, parce que les nombres sont dans le désordre ; on peut donc y remédier en les triant :

On peut aussi regarder s’il n’y a que des « 1 » dans le tableau d’effectifs :

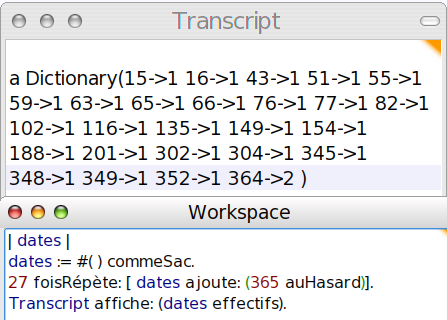
effectifs est un « dictionnaire », dont l’ensemble d’arrivée s’obtient par effectifs values ; le maximum de ces valeurs est donc égal à 1 si aucun anniversaire n’est partagé ; on peut donc stocker ce maximum dans un tableau stats pour représenter ensuite son diagramme en bâtons :

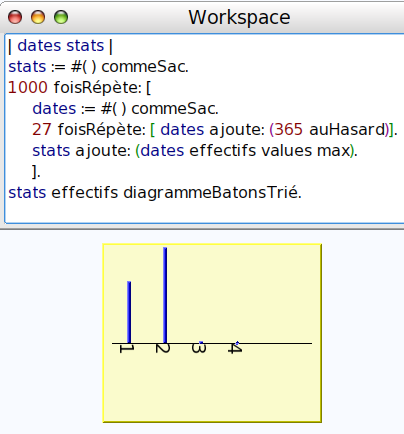
Surprise : Il y a plus de classes de 27 où deux élèves ont le même anniversaire, que de classes où personne ne partage son anniversaire !

La notion d’indépendance probabiliste, et le passage par l’évènement contraire, permettent de calculer la probabilité, avec l’algorithme suivant :

1. on initialise la variable u (terme général d’une suite) à 1.
2. on multiplie u par 364/365 (probabilité que le deuxième élève n’ait pas son anniversaire le même jour que le premier) ;
3. on multiplie u par 363/365 (probabilité que le troisième élève n’ait son anniversaire ni le même jour que le premier, ni le même jour que le second) ;
4. etc (pour n allant de 1 à 27)...
5. Enfin on calcule 1-u (probabilité du contraire)

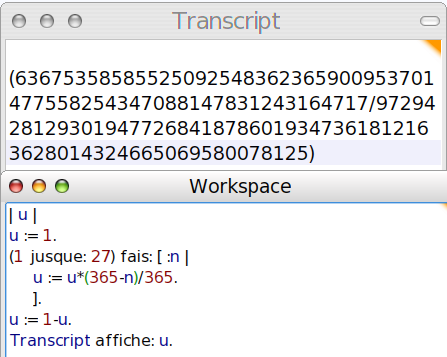
La fraction a des numérateur et dénominateur si grands qu’on a du mal à estimer sa valeur, alors dans ce cas il vaut mieux la transformer en nombre décimal :

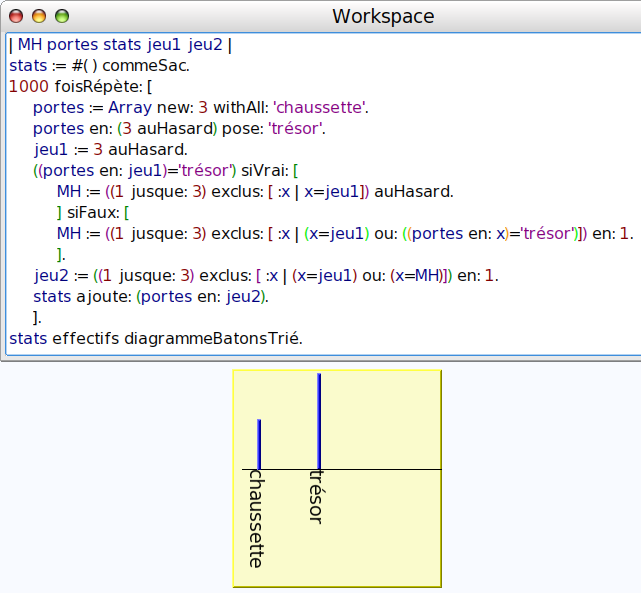
Dans le problème de Monty Hall, un trésor est caché derrière une porte mais le joueur ne sait pas laquelle. Il choisit une porte sans l’ouvrir. Le présentateur ouvre alors une autre porte, derrière laquelle se trouve une chaussette. Le joueur a alors le choix entre les deux stratégies suivantes :

1. Ouvrir la porte choisie au départ ;
2. changer d’avis et ouvrir l’autre porte.

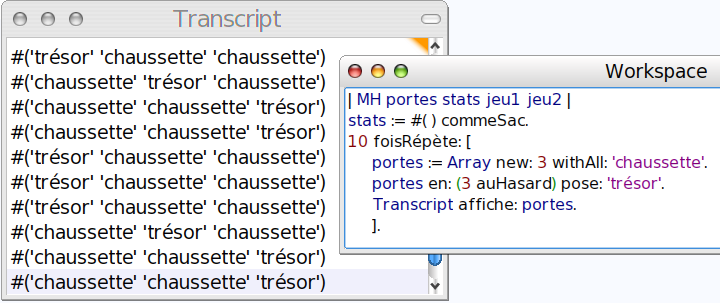
Le plateau de jeu sera donc un tableau dont un élément au hasard contiendra le mot « trésor » et les deux autres, le mot « chaussette ». Le moyen le plus simple pour créer ça [2] est de remplir le tableau avec trois occurences du mot « chaussette » puis de remplacer une de ces occurences au hasard par le mot « trésor » :

Les entiers jeu1, MH et jeu2 sont les propositions du joueur et de l’animateur (Monty Hall), dans l’ordre suivant :

1. jeu1 est la première porte choisie par le joueur (un entier de 1 à 3 au hasard).
2. MH est le numéro de la porte ouverte par Monty Hall, calculé par l’algorithme suivant :
   • Si le joueur a choisi la porte derrière laquelle se trouve le trésor, Monty Hall ouvre une des deux autres portes au hasard ;
   • sinon il ouvre la porte qui n’est ni celle qui cache le trésor, ni celle déjà jouée.
3. jeu2 est le numéro de la porte jouée en dernier.

La stratégie consistant à rejouer la porte choisie au départ n’est pas très payante, puisque qu’elle ne donne le trésor que dans le tiers des cas :

Alors que la stratégie consistant à systématiquement changer de porte (c’est-à-dire choisir la porte qui est à la fois différente de la porte déjà choisie et de la porte déjà ouverte), au contraire, fait gagner dans les deux tiers des cas :