L’une des grandes nouveautés de GeoGebra 3.5 est la possibilité de faire de la régression polynomiale ou exponentielle, et notamment le tracé de droites de régression en sélectionnant un nuage de points avec la souris :

Dans le CarZine, une mine de ressources sur CarMetal, Eric Hakenholz explique dans l’article 104 comment on peut créer des fonctions d’interpolation (mais pas de régression dans le cas présent) sous CarMetal. Bien qu’il proposât de télécharger les macros les plus utiles, nous allons voir comment on peut recréer des macros de ce genre en faisant communiquer CarMetal avec un autre logiciel, en l’occurence un logiciel de calcul formel.

Le choix s’est assez naturellement porté sur l’interface graphique WxMaxima qui pilote le logiciel Maxima, en effet cette interface est très facile à utiliser surtout en classe (choix de boutons sur lesquels cliquer pour réaliser telle ou telle tâche).

Il s’agit ici de réaliser une macro « parabole d’axe vertical par 3 points »

Donc on commence par lancer CarMetal, et créer trois points A, B et C :

L’objet qu’on veut créer est en fait la représentation graphique d’un trinôme [1]. On sait qu’il existe trois nombres $a$, $b$ et $c$ tels que la parabole a pour équation $y=ax^2+bx+c$. Le problème est de déterminer ces nombres. L’information dont on dispose est que la parabole passe par $A$, $B$ et $C$. Donc si on note $x(A)$ et $y(A)$ les coordonnées de $A$, avec des notations analogues pour $B$ et $C$, on sait que

$\left\{ \begin{array}{rcl} ax(A)^2+bx(A)+c&=&y(A) \\ax(B)^2+bx(B)+c&=&y(B) \\ax(C)^2+bx(C)+c&=&y(C) \\ \end{array}\right.$

Système qu’il reste à résoudre. C’est ici qu’intervient Maxima :

Puisqu’on veut résoudre un système, on clique sur ... résoudre !

S’ouvre alors une fenêtre avec deux champs de saisie, l’une pour les équations séparées par des virgules, l’autre pour les variables a, b et c également séparées par des virgules. On remarque qu’il faut mettre le signe de multiplication entre b et x(A) par exemple, et que le carré se note par « ^2 » :

Quand on clique sur « Valider », Maxima calcule presque instantanément la solution du système :

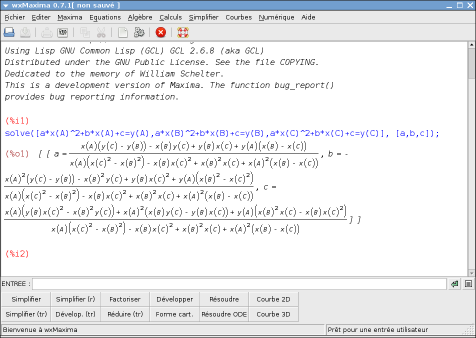
Impressionnant, non ? La fonction « tex » de Maxima permet de l’écrire mieux :

$a={{x\left(A\right)\,\left(y\left(C\right)-y\left(B \right)\right)-x\left(B\right)\,y\left(C\right)+y\left(B\right)\,x \left(C\right)+y\left(A\right)\,\left(x\left(B\right)-x\left(C \right)\right)}\over{x\left(A\right)\,\left(x^2\left(C\right)-x^2 \left(B\right)\right)-x\left(B\right)\,x^2\left(C\right)+x^2\left(B \right)\,x\left(C\right)+x^2\left(A\right)\,\left(x\left(B\right)-x \left(C\right)\right)}}$

$ b=-{{x^2\left(A\right)\,\left(y\left(C \right)-y\left(B\right)\right)-x^2\left(B\right)\,y\left(C\right)+y \left(B\right)\,x^2\left(C\right)+y\left(A\right)\,\left(x^2\left(B \right)-x^2\left(C\right)\right)}\over{x\left(A\right)\,\left(x^2 \left(C\right)-x^2\left(B\right)\right)-x\left(B\right)\,x^2\left(C \right)+x^2\left(B\right)\,x\left(C\right)+x^2\left(A\right)\,\left( x\left(B\right)-x\left(C\right)\right)}}$

$c={{x\left(A\right)\, \left(y\left(B\right)\,x^2\left(C\right)-x^2\left(B\right)\,y\left(C \right)\right)+x^2\left(A\right)\,\left(x\left(B\right)\,y\left(C \right)-y\left(B\right)\,x\left(C\right)\right)+y\left(A\right)\, \left(x^2\left(B\right)\,x\left(C\right)-x\left(B\right)\,x^2\left(C \right)\right)}\over{x\left(A\right)\,\left(x^2\left(C\right)-x^2 \left(B\right)\right)-x\left(B\right)\,x^2\left(C\right)+x^2\left(B \right)\,x\left(C\right)+x^2\left(A\right)\,\left(x\left(B\right)-x \left(C\right)\right)}} $

Il est alors possible de cliquer sur « a » seul (on voit du noir autour de l’expression le définissant). Cette manipulation ressemble au tracé d’un rectangle de sélection :

Ensuite on copie l’équation (par « Control+C » ou « pomme+C » selon le matériel dont on dispose) puis on revient à CarMetal, où on crée une variable « a » (l’icône représente un curseur), qu’on n’oublie pas de nommer « a », et dans le champ « Expression » de l’onglet « numérique » :

on colle (par « Control+V » ou « Pomme+V » selon le matériel) l’expression calculée par Maxima. On a alors 0, ce qui est étonnant : En effet on a copié une égalité, que CarMetal interprête comme une variable booléenne qui est fausse. Il suffit alors d’enlever le « a= » du début de cette expression, et on a la valeur de a, la bonne ! Ensuite on fait pareil avec « b » et « c » et on obtient le fichier suivant :

Pour vérifier, il suffit de créer la représentation graphique d’une fonction f(x) et d’y mettre l’expression

a*x^2+b*x+c

et on a enfin la parabole :

La suite logique, non traitée ici, serait de transformer tout ça en une macro : On crée une macro, on choisit A, B et C comme objets initiaux, et la parabole comme objet final. C’est possible car a, b et c ont été définis en fonction des coordonnées de A, B et C et ne sont donc pas nécessaires pour la macro.

Ce genre de manipulation est extrêmement puissant, à moins d’être capable de trouver mentalement et sans se tromper les formules pour a, b et c [2]...

On peut rêver d’une communication automatique entre les logiciels, sans passer par le copier-coller. C’est possible

– légalement si les deux logiciels sont sous la license GPL 3.0, ce qui est le cas de CarMetal et de Maxima, ça tombe bien
– techniquement puisque Maxima a été incorporé au logiciel Euler Math Toolbox et que Yacas a été incorporé à GeoGebra (ce qui lui permet notamment de faire des factorisations).

Mais le travail de programmeur pour réaliser ça ne semble pas aisé du tout. Ainsi pour construire l’équivalent sous GeoGebra il a fallu faire exactement pareil : copier-coller depuis Maxima [3].

Interpolation « linéaire » ou affine

De même, une régression linéaire sur deux points est une interpolation linéaire; idée très simple mais apparemment peu utilisée...

On souhaite trouver l’expression de la fonction f vérifiant
– f est affine
– f(2)=1
– f(8)=3

On va donc faire de la statistique l’air de rien, en réalisant une régression linéaire sur deux points, de coordonnées respectives (2 ;1) et (8 ;3).

Sur une calculatrice « Ti » [4], on commence par vider le tableau statistique, avec « ClrList » qui se trouve dans l’écran « STAT EDIT » :

Ensuite on refait « STAT EDIT » pour choisir l’option « Edit » qui mène au tableau suivant, dans lequel on entre les abscisses dans la première colonne « L1 » et les ordonnées correspondantes dans la deuxième colonne « L2 » :

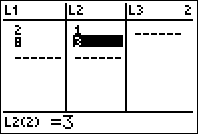
Le calcul de l’équation réduite se fait alors par « LinReg(ax+b) » qui se trouve dans « STAT CALC » :

En sélectionnant ce « LinReg » on voit apparaître « LinReg » dans l’écran de calcul ; il faut alors le compléter par « L1,L2 » (pas le point, la virgule) pour avoir

LinReg L1,L2

qui affiche le résultat :

qui nous apprend que l’équation réduite est $y=\frac{x+1}{3}$. C’est fini !

Si on veut affiner le résultat, comme par exemple transformer en fraction ou représenter graphiquement, cette équation réduite est disponible dans les variables statistiques de la calculatrice : Le bouton « VARS » mène à cette longue liste

où on voit qu’il y a des variables statistiques, ligne 5. Parmi celles-ci

c’est dans la catégorie « EQ » que se trouve l’expression de y en fonction de x. Pour peu qu’on ait fait la manip depuis l’écran « Y= », on a
Y1=.3333333333X+.3333333333

qui permet de représenter la droite.

Cette manip a déjà été montrée avec un certain succès, en seconde, en première L et en première STG...