Le placement de 8 reines sur un échiquier de telle façon que chacune ne soit en prise avec aucune des autres est un classique de programmation. C’est selon le contexte, un exercice sur la récursivité, un exercice sur la gestion des contraintes, et généralement les deux.

On sait que ce problème a « traditionnellement » 92 solutions.
Traditionnellement signifiant ici qu’on se place dans une approche informatique : on fait balayer à la première reine la première colonne et on cherche toutes les positions possibles pour les reines sur les autres colonnes. Travaillant ainsi, mathématiquement plusieurs solutions sont isométriques ce qui fait qu’au final il n’y a que 12 solutions isométriquement différentes (wikipedia).

L’objectif de cet onglet est surtout de mettre en place une fonction JavaScript pour afficher, dans CaRMetal, avec 8 points représentant les 8 reines, les 92 solutions à l’aide d’un curseur allant de 1 à 92.

Quelques mots sur l’algorithme

Nous passerons un peu vite sur la description de l’algorithme de recherche des solutions. Des centaines de pages Web rendent compte de cet exercice, donnons seulement les grandes lignes utilisées.

Puisqu’il n’y a qu’une reine par ligne, on se limite généralement à noter les solutions dans un tableau à une seule dimension. Dans le script suivant JeuEch[i]=j signifie que la reine de la colonne j est en ligne i.

On peut utiliser une fonction pour tester si une position est correcte comme celle-ci :

L’intérêt - théorique ici car l’exécution est très rapide - d’utiliser des booléens est dans leur traitement paresseux : si le premier est vrai le reste n’est pas évalué, de même pour le second.

Ensuite on rempli un tableau à deux dimensions LesSol[92,8] qui pour chaque solution contient les numéros de ligne des reines pour cette solution :

À ce sujet mentionnons une éventuelle difficulté de JavaScript qui a un traitement de la définition des tableaux à double entrée assez éloignée des autres langages - pour l’allocation de la mémoire en particulier - et qui le rend assez inaccessible aux élèves sauf à donner la procédure suivante, générique : on doit déclarer des tableaux de tableaux de colonnes (ou de lignes).

Placer les 92 solutions dans 8 points

La seule raison de cet onglet est la présentation du procédé CarScript qui permet de placer les 92 solutions sur les 8 points qui vont représenter les 8 reines, afin de pouvoir balayer toutes les solutions à l’aide d’un curseur allant de 1 à 92 comme dans la copie d’écran suivante :

Cela signifie que le script se lance sur une figure spécifique - téléchargeable en fin d’article - qui contient un curseur. Le principe est de construire des points dont les coordonnées sont des combinaisons linéaires de booléens de type (n==k) pour k allant de 1 à 92. En fait, même si ce n’est pas indispensable ici, mais parce que ce le sera dans la suite de l’article, plutôt que d’agir directement sur les points, on a choisi d’affecter à 8 expressions de CaRMetal, TR0 à TR7, les ordonnées des points des reines (les abscisses sont fonction des colonnes). Ainsi le script donne ses valeurs aux expressions de CaRMetal, la construction des points reste interne à la partie géométrique du logiciel.

La fonction de transfert du tableau à deux dimensions LesSol[92,8] aux 8 expressions TRx est la suivante :

On place donc dans l’expression CaRMetal « TR »+i, la chaîne solTR qui est une combinaison linéaire des booléens (n==k) affectés de la valeur de la i-ième colonne (position de la reine). Un changement d’échelle (6-2-kTR) est nécessaire pour s’adapter au dessin de l’échiquier. Comme dans tout traitement de ce type des chaînes, la dernière valeur est en dehors de la boucle (la seule différence est la fin de la chaîne qui ne se termine plus par +« + ».

Les expressions TR dans le logiciel sont donc de longues chaînes dont voici un petit extrait :

Pour ne pas encombrer l’ouverture de cet article, la figure n’est pas en ligne, elle est téléchargeable. Mais il est plus amusant de lancer le script sur la figure prévue à cet effet : on voit que le plus long dans ce script est l’affichage de l’échiquier, le reste est quasiment instantané.

// Les 8 reines dans une figure CaRMetal
// 8 points prennent les 92 positions par curseur

// A - partie JS de programmation pure
// Programme standard repris de nombreux sites sur la récursivité

var JeuEch= new Array();

// Comme il n'y a qu'une reine par ligne, traditionnellement,
// on utilise un tableau à une dimension : l'indice de la colonne
// indique le num de la ligne, autrement dit
// JeuEch[i]=j signifie que la reine en colonne i est placée en ligne i

function initJeu(){
	for (i=0; i<8; i=i+1){JeuEch[i]=-1;
	}
	// car en JS les tableaux commencent à 0 d'où init à -1
}

function initTab2(iLgns,iCols){
	var i,j;
	var a = new Array(iLgns);
	for (i=0; i < iLgns; i++){
		a[i] = new Array(iCols);
		for (j=0; j < iCols; j++){
			a[i][j]=0;
		}
	}
	return(a);
}

function PositionOK(lgn,cln){
	// La position (lgn,cln) est OK s'il n'y a pas de reines en lgn avant
	// ni sur les différentes diagonales
	// Souvent les deux derniers OU sont remplacés par un seul avec un abs
	// ils traitent chacun des diagonales descendantes et montantes

	var kt
	for (kt=0; kt<cln; kt=kt+1){
		if ((JeuEch[kt]==lgn) || (lgn-JeuEch[kt]==cln-kt) ||(lgn-JeuEch[kt]==kt-cln)){
			return 0;
		}
	}
	return 1;
}

// La fonction suivante place la Reine de la colonne n
// et remplit aussi le tableau des solutions pour construire les points ensuite

function PlaceReineEnCln(n){
	var i
	if (n>=8) {
		for (u=0; u<8; u=u+1){
			LesSol[nbsol][u]=JeuEch[u];
			// nbsol va de 0 à 91 d'où le ++ aprés
		}
		nbsol++;
	}
	else {for (i=0; i<8; i=i+1){
			if (PositionOK(i,n)==1){
				JeuEch[n]=i;
				PlaceReineEnCln(n+1);
				JeuEch[n]=-1;
			}
		}
	}
}


// B - Partie affichage dans CaRMetal

// On se propose de visualiser les solutions à l'aide d'un
// curseur n : chaque point est donc affecté de 92 positions booléennes différentes.

// Pour l'affichage on se donne l'échiquier suivant dont les cases
// font 2x2 et dont les centres sont de coordonnées paires

function ColorieEch(){
	k=0
	for (i=0; i<8; i=i+1){
		for (j=0; j<8; j=j+1){
			p1=Point(-7+2*j,7-2*i);p2=Point(-5+2*j,7-2*i);
			p3=Point(-5+2*j,5-2*i);p4=Point(-7+2*j,5-2*i);
			SetHide("_p1,_p2,_p3,_p4",true);
			poly=Polygon("_p1,_p2,_p3,_p4");
			if (k==0){SetRGBColor(poly,250,204,130);k=1;
			} else {SetRGBColor(poly,130,204,250);k=0;
			}
		}
		if(k==0) {k=1} else {k=0}
	}
}

// L'idée de base est juste cette fonction c'est tout, le reste est classique

function ConstruitPoints(){
	for (i=0; i<8; i=i+1){
		solTR="";
		for (j=1; j<92; j=j+1){
			kTR=LesSol[j-1][i];
			solTR=solTR+"(n=="+j+")*"+(6-2*kTR)+"+";
		}
		kTR=LesSol[j-1][i];
		solTR=solTR+"(n=="+j+")*"+(6-2*kTR);
		SetExpressionValue("TR"+i,solTR);
	}
}

// Le programme - le plus long est le dessin de l'échiquier ;-)

initJeu();
LesSol=initTab2(92,8);
nbsol=0;
PlaceReineEnCln(0);
ColorieEch();
ConstruitPoints();

Micro Bonus arithmétique

Une propriété élémentaire des carrés latins peut s’appliquer aux solutions des 8 reines. Notons i et j les indices de ligne et colonne des emplacements des reines d’une solution, et 8(i-1)+j le numéro de la case de l’échiquier (de 1 à 64) où est la reine (i,j) . Puisqu’il y a une reine par ligne et une par colonne, les 8 reines prennent les 8 valeurs possibles pour i ainsi que pour j. Il en résulte que dans toutes les solutions, la somme des numéros des 8 reines est une constante, la constante magique du carré latin d’ordre 8 : 2x28+36 = 260.

Anniversaires - Script introductif

Le corps de cet article reprend le thème des coïncidences des anniversaires du document d’accompagnement des programmes. Ce thème a été abordé le mois dernier sur le site de l’IREM de La Réunion par notre collègue Nordine Bernard Toumache avec une utilisation de la TI 83.

La version que l’on va proposer est inspirée d’un échange sur ce sujet entre l’IREM de Toulouse et celui de La Réunion. Monique Gironce, de l’IREM de Toulouse, est bien connue des utilisateurs de CaRMetal par sa production de tutoriaux avec Wink. Avec le groupe qu’elle anime sur les CarScripts, elle a proposé un premier script qui construit, pour une classe de 30 élèves, jusqu’à 100 échantillons de plusieurs dizaines de classes (on peut choisir 100 échantillons de 100 classes par exemple).

Pour des questions d’échelles, le script se lance sur une figure préconstruite. Un des intérêts de ce script est qu’il peut se lancer plusieurs fois sur la même figure, avec des tailles d’échantillons différents, et donc illustrer non seulement la fluctuation entre les échantillons, mais aussi la précision obtenue selon les effectifs des échantillons.

A des fins pédagogiques, en particulier pour des formations continues, le script est volontairement simple et largement commenté. Il est composé d’une fonction principale :

Deux remarques
On notera le choix d’utiliser le tri de javascript (plus efficace que celui qu’on aurait mis en place). C’est une idée de Alain Busser, bien connu des visiteurs de ce site, avec l’argument qu’il est pratique en classe d’utiliser ces fonctionnalités pré-construites, pour passer plus de temps sur ce que l’on veut enseigner (quartiles etc).
Cette remarque rend compte aussi que ce thème circule entre Toulouse et La Réunion depuis un moment et que chacun a apporté un élément à la production finale.

et du corps du script ...

La visibilité du résultat est plus grande si on trace des segments. D’où une initialisation (lignes 35 à 38) pour avoir le premier point du tracé avant de reprendre le tout dans une boucle pour la construction du segment [ab].
Toujours dans ce contexte de formation continue, on notera une sortie console en même temps que la construction du graphique. Pour une lisibilité optimale à l’écran, on utilise les points I et J construits préalablement, qui sont manipulables pour s’adapter à l’écran, et le nombre d’échantillons.

L’entête du script rappelle la procédure pour changer de couleur à chaque nouveau lancement du script.

//Ouvrir le fichier BaseAnniversaires.zir.
//Avant de lancer une première fois le script, utiliser la palette de droite du fichier pour choisir les options par défaut des futures constructions : des points avec des noms "non affiches" ; puis les points et les segments d'une même couleur.
//On peut relancer le script une seconde fois, une troisieme ... sans annuler les effets du premier : changer auparavant la couleur des points et des segments pour plus de clarte.
//Pour une meilleure lisibilite du graphique, bouger éventuellement le point J et zoomer.

function FrequencePourEchantillon(t){
	//	t designe la taille de l'echantillon, donc le nombre de classes.
	var N=0;
	//	Un compteur est initialise a zero.
	for (j=0; j<t; j=j+1){

		tab=new Array
		for (i=1; i<31; i=i+1){
			tab[i]=Math.ceil(365*Math.random());
		}
		//Construit une liste de 30 nombres au hasard (entre 1 et 365)
		tab=tab.sort();
		//dont les elements sont tries par ordre croissant

		for (k=1; k<30; k=k+1){
			if (tab[k]==tab[k+1]){
				k=31;
				//A la premiere coincidence, sortie de boucle !
				N=N+1;
				//et le compteur augmente de 1.
			}
		}
	}
	return N/t;
}

t=Input("taille de l'échantillon ?");
nb=Input("nombre d'échantillons ?");

f=FrequencePourEchantillon(t);
a=Point(1,"_f*y(J)");SetThickness(a,"thick");SetPointType(a,"point");
//Creation du premier point de coordonnees (1;f)
Println("echantillon numéro 1 : fréquence = "+f );

for (n=2; n<=nb; n=n+1){
	b=a;
	//	Recopie le contenu de la variable a dans b.
	f=FrequencePourEchantillon(t);
	Println("echantillon numéro "+n+" : fréquence = "+f );
	a=Point(n,"_f*y(J)");SetThickness(a,"thick");SetPointType(a,"point");
	//	Creation des points de coordonnees (n;f).
	s=Segment(a,b);
}

Ce qui donne pour un premier lancement du script (100 échantillons de 100 classes chacun) :

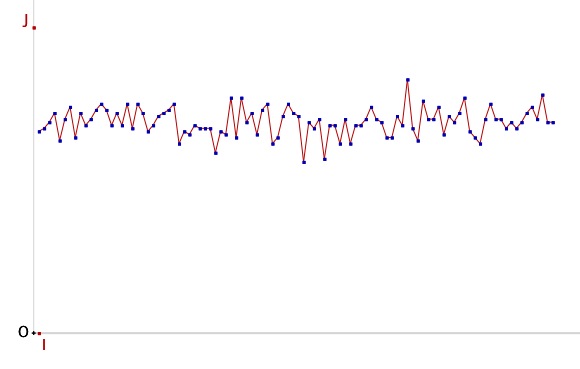
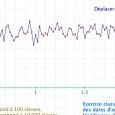
On peut conserver le nombre d’échantillons et faire varier leurs effectifs. Voici par exemple en vert des effectifs de 400 classes par échantillon et en rouge des effectifs de seulement 40 classes par échantillon. Il y a matière à expérimentation, exploration et débat sur le sens de ces observations.

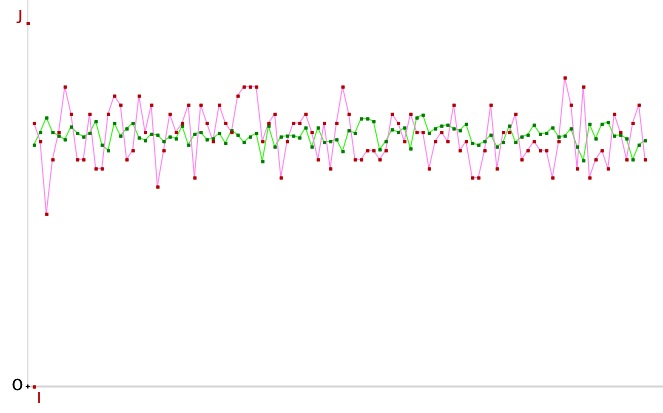
Bien entendu on pourrait ensuite ajouter de nombreuses données à l’intérieur du script. Le choix du groupe de travail de l’IREM de Toulouse d’utiliser la sortie console est surtout de montrer cette possibilité aux collègues lors de formations.

Dans les onglets suivants, on se propose de donner une dimension dynamique à ce premier script, d’abord en permettant de choisir le nombre d’élèves par classe au cours du script (en fait la seule originalité de cet article) puis par le maintien d’un tirage régulier toutes les secondes, de permettre d’utiliser effectivement de manière dynamique ce choix du nombre d’élèves par classe pendant l’exécution du script. Le résultat va être une simulation de l’activité avec manipulation directe sur le nombre d’élèves par classe, puis sur les effectifs des échantillons également.

Anniversaire dynamique - Première approche

On se propose de se donner la possibilité de choisir le nombre d’élèves par classe. Dans cet exercice transitoire, on se limite à la production d’une seule série de 100 échantillons de 100 classes pour détailler le principe. Dans les onglets suivants on rendra la simulation plus conforme à ce que l’on attend, avec un échantillonnage régulièrement renouvelé.

On choisit des classes de 20 à 36 élèves. Le principe consiste à faire des tirages de 36 élèves et de comptabiliser les coïncidences dans un tableau, à partir de 20 élèves. La fonction Random étant équirépartie, a priori ce choix n’apporte pas de perturbation dans les résultats, les tirages de nombres aléatoires sont simplement pris dans des tranches particulières.

La fonction principale est la suivante (commentée ci-dessous) :

Le tableau coïncide comptabilise sur les 100 lancers, une coïncidence d’anniversaire (la première rencontrée) pour l’élève j avec les élèves précédents [lignes 15 à 21]. Ensuite, à partir de 20 élèves , le tableau s somme les coïncidences [lignes 24 et 25]. Ainsi s[k] est le nombres de coïncidences d’anniversaires pour une classe de k élèves dans ces 100 échantillons. Ce tableau est retourné par la fonction.

Exercice : reprendre l’astuce de Alain Busser, vue à l’onglet précédent, pour traiter les coïncidences plus rapidement.

Ensuite on procède exactement comme dans le traitement des 8 reines, en créant une chaîne de caractère qui va être une des coordonnées booléennes d’un point [lignes 31 à 35].

Le programme principal se termine par l’affichage d’un segment. Pour montrer une autre possibilité de construction de ce segment, on a choisi une écriture plus courte mais théoriquement plus gourmande en temps d’exécution. Pour éviter d’écrire deux fois les lignes 30 à 34, (choix de l’onglet précédent) on utilise un if pour éviter la première itération [lignes 36 à 38 et 40] ce qui ajoute 100 tests conditionnels (instantanés en fait). On peut choisir l’option de l’onglet précédent (en plaçant alors le premier point dans la variable b).

// Les anniversaires pour une classe de 24 à 36 élèves
// version semi dynamique (ou semi statique)

function Echantillon(){
	coincide=new Array();
	s=new Array();
	for (i=1; i<37; i=i+1){coincide[i]=0;s[i]=0;}
	
	for (ech=0; ech<100; ech=ech+1){
		var pasegal=true;
		elev=new Array();
		for (i=1; i<37; i=i+1){elev[i]=Math.ceil(365*Math.random());	}
		j=1;
		while (pasegal && (j<37)){
			j=j+1;i=1;
			do{
				if (elev[i]==elev[j]){coincide[j]=coincide[j]+1;
					pasegal=false;
				} else {i=i+1}
			}while (pasegal && (i<j))
		}
	}
	for (k=1; k<21; k=k+1){s[20]=s[20]+coincide[k];}
	for (k=21;k<37;k=k+1) {s[k]=s[k-1]+coincide[k];}
	return s;
}

for (t=1; t<101; t=t+1){	
	ch=Echantillon();
	sol="";
	for (u3=20; u3<36; u3=u3+1){k3=ch[u3];
		sol=sol+"(n=="+u3+")*"+k3+"/100+";}
	k3=ch[u3];sol=sol+"(n=="+u3+")*"+k3+"/100";
	
	a=Point(t/50,"_sol");
	SetPointType(a,"point");SetColor(a,"red");SetThickness(a,"thick");
	if (t>1){s=Segment(a,b);SetColor(s,"blue");}
	
	b=a;
}

On notera l’affectation directe des points. En effet dans cette figure, les points solutions ne sont construits en fait qu’une fois, et il n’y a pas de rafraîchissement à effectuer : la modification de n s’applique hors du script : il n’est pas nécessaire de passer par l’utilisation des expressions.

Le résultat est encourageant : on peut bien faire varier le nombre d’élèves par classe, et on visualise 100 échantillons de 100 classes dans chaque cas. Mais les tirages ne sont pas réactualisés : quand on fait varier le curseur, on repasse par les mêmes valeurs comme on peut le voir dans la vidéo suivante.

Il faut donc aller plus loin pour avoir une simulation véritablement dynamique. C’est l’objectif du prochain onglet.

Anniversaires dynamiques - 1. Fluctuation des échantillonnages

On veut cette fois enrichir la figure d’un tirage aléatoire régulier des différents échantillons. Dans la figure suivante on a choisi 20 échantillons (tranches dans le script) de 100 classes de 20 à 36 élèves soit une amplitude de 17. Comme dans l’exemple des reines, la figure initiale est largement préparée pour accueillir le script qui va lui être appliquer : il y a 17 expressions TRx, une par nombre d’élèves par classe, et 20 points Axx pour les 20 échantillons. Les segments sont construits directement dans la figure.

Amélioration possible du script
L’utilisation des expressions TRxx vient du fait qu’au moment où ce script a été réalisé, la fonction Move, pour déplacer un point à l’écran par script, n’acceptait pas les coordonnées utilisant des booléens. Quand cette fonctionnalité sera disponible, la figure serait à reprendre car plus facile à réaliser.

En effet ici nous avons opté par un rafraîchissement interne au moteur géométrique, en définissant les coordonnées à partir des expressions TRx sous la forme :

où M est un point qui tourne sur un cercle. Cet artifice - de d(M) qui indique le mouvement de M dont l’utilisation est détaillée ici - permet de tester s’il se passe quelque chose à l’écran et donc force le rafraîchissement du point dans ce cas, ce que je n’ai pas su réaliser directement dans le script. Il est probablement possible de réaliser quelque chose d’un peu plus simple.

La figure initiale est plus complète que la précédente. Dans la copie d’écran ci-dessous, les points Axx sont initialement sur l’axe des abscisses en vert fluo.

On y a ajouté le calcul de la valeur théorique de la probabilités d’une coïncidence (au moins) en fonction du nombre d’élèves. Cette expression est construite préalablement par l’application du script suivant :

que chacun peut tester sur une figure de base (curseur + expression) en copiant le script suivant (et vérifier en activant les sorties « console texte » mises en commentaires)

// Valeur théorique des coincidences pour les anniversaires
// Calcul indépendant des autres scripts
// n'applique à une figure qui a un curseur entier n de 20 à 36
// et une expression nommée ValTh

// 1. Le calcul

annivth=new Array()

v=1;
for (i=1; i<20; i=i+1){v=v*(1-i/365)}

annivth[0]=1-v;
// Println("Pour 20 :"+annivth[0]);
for (j=20; j<36; j=j+1){v=v*(1-j/365);
	annivth[j-19]=1-v;
	//	Println("Pour "+j+" : "+annivth[j-20]);
}

// 2. La mise en chaîne

solth="";
for (k=20; k<36; k=k+1){
	ekri=annivth[k-20];solth=solth+"(n=="+k+")*"+ekri+"+";}

ekri=annivth[k-20];
solth=solth+"(n=="+k+")*"+ekri;

// Println(solth);

SetExpressionValue("ValTh",solth);

Dans l’onglet précédent, on avait choisi de travailler avec une fonction qui calculait sur un seul échantillon de 100 classes. Cette fois on enrichit la fonction pour travailler sur les 20 échantillons à la fois. On utilise donc un tableau à deux dimensions (que l’on initialise avec la fonction déjà vue avec les 8 reines).

Comme il est prévu d’autres utilisations, utilisant plusieurs variables de cette structure de tableau, on a choisi cette fois d’optimiser la mémoire. La variable coincidence de l’onglet précédent était un tableau à 36 variables alors qu’on n’utilisait que les 17 dernières variables seulement. Cette fois on choisit d’utiliser un tableau LeTab[20,17] d’où une indiciation adaptée.

La fonction Echantillon de l’onglet précédent est transformée en GrandEchant qui traite les 20 échantillons à la fois (coincidence est remplacé par LeTab). La fonction ne renvoie pas un tableau, celui-ci est désormais une variable globale.

Remarques :
1. On notera une différence avec l’onglet précédent sur les 20 premiers élèves : dans la ligne 29, on engrange directement toutes les coïncidences avant 20 élèves alors que dans l’onglet précédent, ce n’est pas le cas de la ligne 18 correspondante. Cela se faisait dans la boucle de la ligne 24.
2. Tenant compte de cette modification, là encore on peut choisir d’améliorer le remplissage du tableau par l’utilisation du sort de JavaScript.

Le corps principal du script est intégré dans une boucle qui teste si l’utilisateur clique pour stopper le script. La case à cocher « Continuer » est une variable CaRMetal qui s’appelle « cont ».

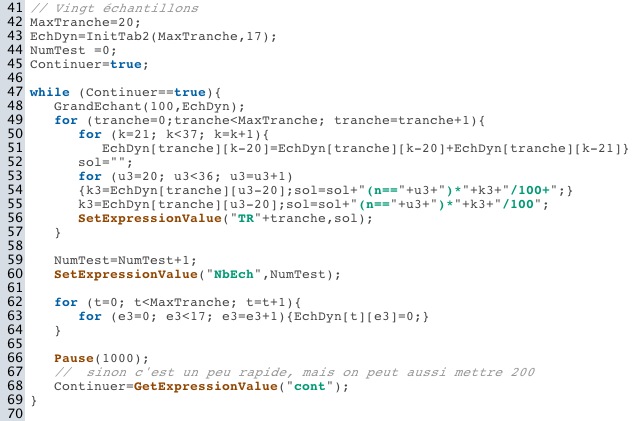
La ligne 51 du corps principal correspond à la ligne 25 du script de l’onglet précédent. La technique montrée dans l’onglet des 8 reines ne prend seulement que les cinq lignes 52 à 56.

Puisque l’on est dans une boucle « infinie », il faut réinitialiser le tableau EchDyn avant chaque nouvel usage, ce qui se fait dans les lignes 61 à 63.

Ce script illustre bien l’imbrication que l’on peut produire entre une figure - préparée pour l’application d’un script et les possibilités des Carscripts. Les points Axx attendent, pour s’actualiser, de nouvelles valeurs des expressions TRx données par le script. Les segments sont préalablement construits. Un autre script a été appliqué pour le suivi de la valeur théorique en fonction du curseur n.

Au moment de la mise en ligne de cet article, on ne peut pas lancer un script en ligne dans une figure, d’où cette vidéo (26 s - 2 Mo) qui rend compte du fonctionnement de ce script sur cette figure.

// Ce script se lance sur AnnivDyn1IREM
// Ici on teste plusieurs fois 20 échantillons de 100 classes

var elev= new Array();
function InitTab2(iLgns,iCols){
	var i,j;
	var a = new Array(iLgns);
	for (i=0; i < iLgns; i++){
		a[i] = new Array(iCols);
		for (j=0; j < iCols; j++){
			a[i][j]=0;
		}
	}
	return(a);
}

function GrandEchant(echMax,LeTab){
	// Remplir chaque échantillon de echMax classes d'élèves
	for (ech=0; ech<echMax; ech=ech+1){
		for (tranche=0;tranche<MaxTranche; tranche=tranche+1){
			pasegal=true;
			for (i=1; i<37; i=i+1){elev[i]=Math.ceil(365*Math.random());
			}
			j=1;
			while (pasegal && (j<37)){
				j=j+1;i=1;
				do{
					if (elev[i]==elev[j]){
						pasegal=false;
						if (j<20){LeTab[tranche][0]=LeTab[tranche][0]+1;

						} else {LeTab[tranche][j-20]=LeTab[tranche][j-20]+1;
						}
					} else {i=i+1}
				}while (pasegal && (i<j))
			}
		}
	}
}

// Vingt échantillons
MaxTranche=20;
EchDyn=InitTab2(MaxTranche,17);
NumTest =0;
Continuer=true;

while (Continuer==true){
	GrandEchant(100,EchDyn);
	for (tranche=0;tranche<MaxTranche; tranche=tranche+1){
		for (k=21; k<37; k=k+1){EchDyn[tranche][k-20]=EchDyn[tranche][k-20]+EchDyn[tranche][k-21]}
		sol="";
		for (u3=20; u3<36; u3=u3+1)
		{k3=EchDyn[tranche][u3-20];sol=sol+"(n=="+u3+")*"+k3+"/100+";
		}
		k3=EchDyn[tranche][u3-20];sol=sol+"(n=="+u3+")*"+k3+"/100";
		SetExpressionValue("TR"+tranche,sol);
	}

	NumTest=NumTest+1;
	SetExpressionValue("NbEch",NumTest);

	for (t=0; t<MaxTranche; t=t+1){
		for (e3=0; e3<17; e3=e3+1){EchDyn[t][e3]=0;
		}
	}

	Pause(1000);
	//	 sinon c'est un peu rapide, mais on peut aussi mettre 200
	Continuer=GetExpressionValue("cont");
}

On notera que la fonction GrandEchant prend le paramètre 100 alors que cela pourrait être une variable. Comme on le voit avec le nombre 100 placé en chaîne de caractère dans les lignes 53 et 54, dans cette figure l’effectif des échantillons est constant. On ajoutera un curseur pour l’effectif dans l’onglet suivant.

Anniversaires dynamiques - 2. Modification des effectifs

La modification à apporter pour mettre l’effectif en paramètre est minime. Mais on a choisi de la présenter séparément, comme enrichissement de la figure précédente et, cognitivement, comme préparation à la figure suivante.

Il faut donc ajouter un curseur d’effectif et transformer un texte en expression (celui qui annonce l’effectif) :

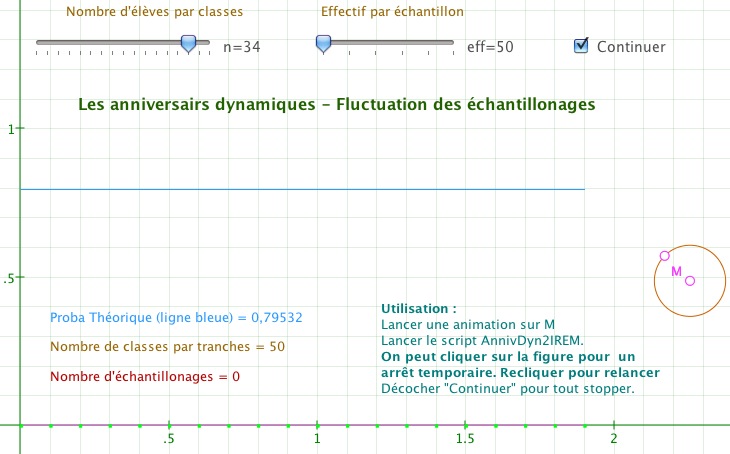
Et la modification du script est minime également :

Il y a l’ajout de la variable ChEff (choix de l’effectif) en ligne 48 qui lit le nouveaucurseur eff de la figure. Puis le remplacement de la constante 100 par ChEff en lignes 55 et 56 et c’est tout. On peut enlever la pause car quand l’effectif est de 200 à 300 les calculs sont suffisament longs pour que ce ne soit pas la peine de ralentir la boucle.

Voici une vidéo (57 s - 4,7 Mo) de ce que produit le script AnnivDyn2IREM sur la figure du même nom (dans le fichier zippé en fin d’article).

L’onglet suivant contient une autre variante pour accumuler les classes dans les échantillons. L’essentiel a été déjà fait dans le script de Dyn1.

Anniversaires dynamiques - 3. Convergence

On se propose d’accumuler désormais les effectifs des échantillons. La figure est quasiment la même que dans l’onglet Dyn1 (seule une variable supplémentaire apparait)

Le script comporte lui une modification plus profonde, en particulier on distingue l’ajout d’un nouvel effectif (AjoutDyn) de l’effectif en cours (EchDyn des scripts précédents). Il y aura donc deux variables globales de type tableau à deux dimensions :

De même la variable NbreEch est nouvelle, c’est l’effectif de chaque échantillon. Cette variable globale est modifiée - même si ce n’est pas très heureux - dans la fonction GrandEchant : lignes 34 et 35 qui mettent à jour la variable CaRMetal clpt (pour « classes par tranche »).

La suite du corps du script commence par un tirage initial de 100 classes pour chacun des 20 échantillons (« tranches » dans le script). Pour cela, on reprend hors de la boucle Continuer, les lignes 48 à 56 du script de l’onglet Dyn1.

La partie nouvelle du script est la nouvelle boucle Continuer :

On effectue de nouveaux tirages (ici par série de 100 classes mais on peut tester avec 50) qui sont placés dans la variable AjoutDyn. (ligne 65). De par la ligne 27 de GrandEchant, on a déjà dit que jusqu’à 20 on a sommé toutes les coïncidences.

La ligne 68 met à jour, en fonction des nouveaux tirages de AjoutDyn, les valeurs de EchDyn pour le cas n=20 (indice [0]). On place ensuite dans une même boucle (lignes 70 et 71) le calcul final de AjoutDyn (qui reprend la ligne 50 du script de Dyn1) pour les classes de 21 à 36 élèves et la mise à jour de EchDyn qui devient désormais l’effectif global de chaque échantillon. Les lignes 72 à 78 ne sont modifiés que par la variable NbreEch (à la place de 100). Enfin la remise à zéro est bien entendu sur la variable AjoutDyn. Si l’écriture est un peu technique, l’algorithme sous-jacnet reste élémentaire.

Voici ce que donne ce script appliqué à cette figure (disponible dans les fichiers en fin d’article).

// Ce script se lance sur AnnivDyn3IREM

var elev= new Array();
function InitTab(iLgns,iCols){
	var i,j;
	var a = new Array(iLgns);
	for (i=0; i < iLgns; i++){
		a[i] = new Array(iCols);
		for (j=0; j < iCols; j++){
			a[i][j]=0;
		}
	}
	return(a);
}

function GrandEchant(echMax,LeTab){
	for (ech=0; ech<echMax; ech=ech+1){
		for (tranche=0;tranche<MaxTranche; tranche=tranche+1){
			pasegal=true;
			for (i=1; i<37; i=i+1){elev[i]=Math.ceil(365*Math.random());}
			j=1;
			while (pasegal && (j<37)){
				j=j+1;i=1;
				do{
					if (elev[i]==elev[j]){
						pasegal=false;
						if (j<20){LeTab[tranche][0]=LeTab[tranche][0]+1;
						} else {LeTab[tranche][j-20]=LeTab[tranche][j-20]+1;}
					} else {i=i+1}
				}while (pasegal && (i<j))
			}
		}
	}
	NbreEch=NbreEch+echMax;
	SetExpressionValue("clpt",NbreEch);
}

// Vingt tranches d'échantillons
MaxTranche=20;
NbreEch=0;
EchDyn=InitTab(MaxTranche,17);
AjoutDyn=InitTab(MaxTranche,17);


// L'initialisation par un effectif de 100 classes dans chaque tranche)
GrandEchant(100,EchDyn);

for (tranche=0;tranche<MaxTranche; tranche=tranche+1){
	for (k=21; k<37; k=k+1){EchDyn[tranche][k-20]=EchDyn[tranche][k-20]+EchDyn[tranche][k-21]}
	sol="";
	for (u3=20; u3<36; u3=u3+1){k3=EchDyn[tranche][u3-20];
		sol=sol+"(n=="+u3+")*"+k3+"/100+";}
	k3=EchDyn[tranche][u3-20];sol=sol+"(n=="+u3+")*"+k3+"/100";
	SetExpressionValue("TR"+tranche,sol);
}


NumTest=1;

Continuer=true;
while (Continuer==true){
	GrandEchant(100,AjoutDyn);
	// on pourrait choisir d'ajouter 50 ou 20 élèves à la fois.
	for (tranche=0;tranche<MaxTranche; tranche=tranche+1){
		EchDyn[tranche][0]=EchDyn[tranche][0]+AjoutDyn[tranche][0];
		for (k=21; k<37; k=k+1){AjoutDyn[tranche][k-20]=AjoutDyn[tranche][k-20]+AjoutDyn[tranche][k-21];
			EchDyn[tranche][k-20]=EchDyn[tranche][k-20]+AjoutDyn[tranche][k-20]}
		sol="";
		for (u3=20; u3<36; u3=u3+1){k3=EchDyn[tranche][u3-20];
			sol=sol+"(n=="+u3+")*"+k3+"/"+NbreEch+"+";}
		k3=EchDyn[tranche][u3-20];sol=sol+"(n=="+u3+")*"+k3+"/"+NbreEch;
		SetExpressionValue("TR"+tranche,sol);
	}
	NumTest=NumTest+1;
	SetExpressionValue("NbEch",NumTest);
	for (t=0; t<MaxTranche; t=t+1){
		for (e3=0; e3<17; e3=e3+1){
			AjoutDyn[t][e3]=0;}
	}
	Pause(200);
	//	si on ajoute 100 élèves à la fois on peut ne pas mettre de pause.
	Continuer=GetExpressionValue("cont");
}

La mise en place de cette seconde variable AjoutDyn permettrait bien d’autres variations. On pourrait déjà mettre un curseur pour faire varier les ajouts de 20 à 100 par tranche de 20. Comme à l’onglet précédent, il n’y a que quelques lignes à modifier dans le script précédent. Mais on peut aussi envisager d’autres utilisations comme l’ajout et le retrait de tirages pour conserver un nombre constant et avoir une approche différente de la fluctuation des échantillonnages.