Pour entrer dans le sujet, je voudrais faire un petit tour dans les dictionnaires, histoire de baliser le terrain. Les mathématiciens parmi vous voudrons bien m’excuser, mais ma pratique de cet objet conceptuel particulier qu’est le nombre est vraiment très instinctive. J’utilise les nombres comme des outils aussi puissants et aussi naturels que le sont mes mains, et je ne me suis jamais posé de questions métaphysiques à leur propos. J’ai donc entrepris l’exercice bizarre qui consiste à chercher des définitions pour comprendre cette évidence qu’est le nombre.

Le résultat est intriguant. Si on écarte les tentatives de définitions tautologiques du genre « le nombre est la notion qui permet de dénombrer des choses » (Larousse !), on arrive à des définitions honnêtes qui avouent que le nombre est une notion première, une notion fondamentale de l’entendement et qu’on ne peut le définir. Bien sûr, des articles encyclopédiques entiers vont ensuite en décrire les propriétés, les particularités. Mais le concept global de nombre, qui me semblait pourtant transparent comme l’eau claire, est en fait très difficile à enfermer dans une définition.

Pour essayer d’y voir plus clair, je me suis rabattu sur le terme « numération » et, à voir la définition, j’en ai conclu que je n’étais pas le premier à faire ce chemin. La numération en effet, est définie comme « la manière de rendre sensible la notion abstraite de nombre, et d’en conserver la mémoire ». La numération, c’est donc le moyen qu’on a trouvé pour apprivoiser le nombre. Et les différents systèmes de numération sont les outils inventés par les hommes pour parvenir à manipuler les nombres.

Ce concept d’outil est central, il renvoie à ce que le psychologue Lev Vygotsky a qualifié d’outils psychologiques. Il s’agit de tous les ensembles de signes élaborés par les hommes au cours de leur histoire culturelle, qui servent de support aux connaissances. Le langage est l’un d’eux, le premier certainement, mais il en existe bien d’autres comme l’écriture, les conventions picturales comme la perspective, les conventions cartographiques, les notations musicales, la géométrie et bien sûr, les systèmes de numération.

Il serait réducteur de ne considérer ces outils que comme des supports pratiques pour échanger à propos de connaissances qui existeraient dans nos esprits, indépendamment d’eux. Plus que des vecteurs de communication à propos des connaissances, les outils psychologiques sont en réalité la condition nécessaire à la connaissance, ils nous permettent d’appréhender le monde, de nous le représenter pour pouvoir le connaître. C’est vrai pour le langage, sans lequel on ne peut pas connaître ce qui est en dehors de notre expérience sensible, c’est vrai également pour les systèmes de numération, sans lesquels les nombres nous sont quasiment inaccessibles.

Abandonnons les nombres quelques minutes pour délimiter l’autre extrémité de notre champ de réflexion, celle des fonctions cognitives qui nous permettent de nous représenter le monde et de manipuler mentalement nos connaissances.

Le concept de représentation est central en psychologie cognitive. Pas beaucoup plus évident à définir que le concept de nombre, pour les mêmes raisons : il a un petit parfum d’évidence qui le rend rétif à toute tentative d’enfermement. On peut néanmoins le voir comme l’action par laquelle on rend présent à l’esprit une expérience sensible ou une idée. En d’autres termes, c’est le contenu de notre mémoire quand elle ne sous échappe pas, c’est ce qui tourne dans nos têtes quand on réfléchit, c’est le sens qu’on donne à ce qu’on perçoit.

Les psychologues qui travaillent sur le raisonnement humain ont montré que lorsqu’on est engagé dans une tâche de résolution de problème, nous ne nous appuyons pas seulement sur des représentations internes (ce qui est dans nos têtes : mémoire, raisonnement, capacités attentionnelles), mais aussi sur des représentations externes qui sont constituées d’indices physiques présents dans l’environnement perceptif.

Pour illustrer cette opposition entre représentation interne et représentation externe, on peut penser à ce qui va empêcher un automobiliste de s’engager dans une rue qu’il n’a pas le droit d’emprunter. Une grosse barrière dressée bien au milieu l’empêchera de passer, mais un panneau circulaire, rouge avec une bande blanche, placé sur le côté, aura le même effet, à condition qu’il connaisse le code de la route, qu’il ne l’ait pas oublié et qu’il ait pensé à regarder là où se trouve le signal en question.

Le langage de la barrière est universel, il ne nécessite aucun travail intellectuel autre que de constater se présence : l’impossibilité de passer est traitée grâce à une représentation externe. Le langage du panneau, par contre, c’est-à-dire le recours aux conventions du code de la route, repose sur une représentation interne, il nécessite une activité cognitive non négligeable.

C’est en suivant ce fil d’Ariane, que nous allons à présent entreprendre l’analyse systématique des systèmes de numération. Nous allons chercher, pour les différents systèmes de numération, quelles sont leurs propriétés qui nécessitent une représentation interne et quelles sont celles qui reposent sur une représentation externe.

La première étape de cette analyse s’interroge sur la dimensionnalité des systèmes de numération : combien de dimensions sont nécessaires pour coder les nombres ?

Systèmes 1D

Les systèmes de numération les plus simples ne comportent qu’une dimension. Tous les systèmes de numération primitifs fonctionnent de cette façon et, pour la plupart d’entre eux, la dimension en question est la quantité : une pierre correspond à une unité, deux pierres à deux unités, etc. On trouve des traces très anciennes de ce type de numération, comme des os ou des bois de cervidés comportant des séries d’encoches qui témoignent d’une utilisation des nombres depuis au moins 30 000 ans.

Il existe également des systèmes numériques 1D dont la dimension signifiante est la position de différentes parties du corps (doigts, poignet, coude, parties du visage, etc.). On en trouve des exemples chez certains peuples de Papouasie Nouvelle-Guinée, dans les îles Torres en Mélanésie ou encore chez les indiens Chacos au Paraguay.

La plupart des systèmes 1D, particulièrement ceux basés sur la propriété de quantité, sont très efficaces pour rendre compte des petits nombres, du fait de la proportionnalité qu’il y a entre le nombre d’objets et la valeur numérique représentée. Les comparaisons ne nécessitent aucune gymnastique conceptuelle autre que « il y en a plus » ou « il y en a moins ». Et en plus, ces systèmes de numération rendent les additions et les soustractions très faciles, ne requérant aucune connaissance arithmétique puisqu’on peut les effectuer en ajoutant ou en enlevant des marques de notation.

Du point de vue de la représentation que ces systèmes permettent de se faire des nombres, les systèmes 1D dont la dimension est la quantité sont clairement externes : c’est l’exploration perceptive directe de la quantité d’objets qui indique le nombre ; il n’y a aucune règle de correspondance à mémoriser, aucun code.

Pour les systèmes 1D basés sur la position d’un segment corporel, la représentation sera plus interne, dans la mesure où la relation entre le poignet et le chiffre 6, ou l’œil et le chiffre 13, n’est pas évidente. Elle comporte quand même une dimension externe importante puisque, jusqu’à 5, c’est le nombre de doigts, et ensuite on remonte le bras, on traverse le visage : plus on a remonté le long du bras, plus le nombre signifié est important.

Ces systèmes très efficaces pour les petites valeurs perdent tout leur intérêt dès qu’il devient nécessaire de traiter des grands nombres. Voyons comment on peut représenter un nombre relativement important, par exemple 447, avec un système de ce type :

Systèmes 1x1D

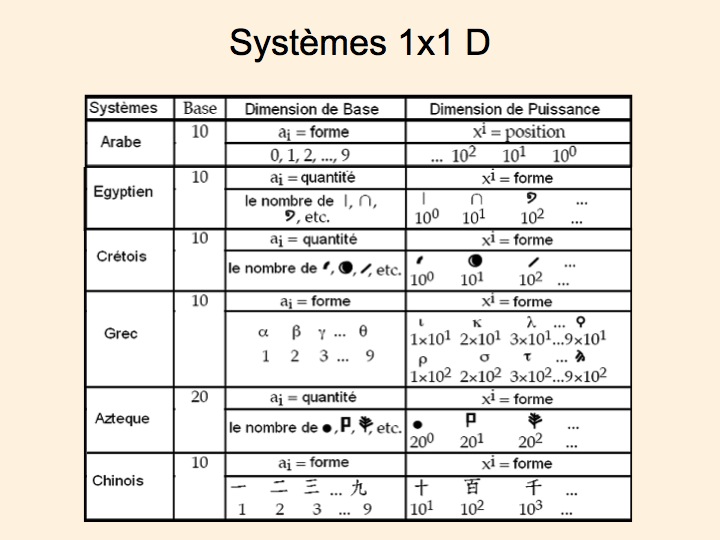
Pour traiter les grands nombres, il faut plus d’une dimension. Par exemple une dimension de base, qui assurera la représentation élémentaire, et une dimension de puissance qui va décomposer le nombre en groupes hiérarchiques sur la base. Les deux dimensions peuvent être représentées par différentes propriétés qui sont le plus souvent la forme, la position ou la quantité.

Exemples :

• • Dans le système de numération arabe, qui est un système 1x1D, la dimension de base est représentée par la forme des signes (1, 2, 3, ...), la base est de 10, et la dimension de puissance est représentée par la position (première position pour $10^0$, deuxième position pour $10^1$, troisième position pour $10^2$, etc.).
  • Dans le système de numération égyptien, en base 10 également, la dimension de base est la quantité et la dimension de puissance est la forme (avec des symboles différents pour $10^0$, $10^1$, $10^2$, etc.).

Les trois propriétés couramment utilisées dans ces différents systèmes de numération ne sont pas identiques du point de vue de la représentation qu’elles permettent. La quantité, on l’a vu pour les systèmes 1D, permet une représentation externe du fait du rapport direct entre le nombre de signes et la valeur numérique figurée.

La propriété de position est également externe : ce sont les relations de voisinage topologique entre les signes, relations directement observables, qui porteront les indices pertinents pour se représenter le nombre : $Base^0$ en première position, $Base^1$ en deuxième position, $Base^2$ en troisième position, etc. À noter que dans tous les systèmes présentés, cette propriété de position ne sert jamais à rendre compte de la dimension de base. Quand elle est utilisée, c’est pour signifier la dimension de puissance. Cela apporte un avantage non négligeable : on peut estimer l’ordre de grandeur d’un nombre, simplement en vérifiant combien de places sont utilisées.

La propriété de forme, par contre, nécessite un traitement interne : c’est en vertu d’un code arbitraire que le signe 2 signifie le nombre deux en notation arabe, et pas le nombre sept ; que le signe $\gamma$ (gamma) signifie le nombre trois en notation grecque, ou que le signe en forme de spirale signifie le nombre 100 en notation égyptienne.

On peut noter toutefois que dans certains systèmes, la forme a été choisie de façon à évoquer un rapport sémantique avec la dimension du nombre figuré : en égyptien, 1000 est représenté par une fleur de lotus, 10 000 par un doigt pointé vers les étoiles, 100 000 par une grenouille, dont les têtards sont innombrables, etc.

Un autre paramètre est à considérer dans le cas des systèmes 1x1D. En effet, indépendamment du fait que telle ou telle propriété offre plus ou moins d’indices externes pour faciliter la représentation, il faut considérer la façon dont on parvient à discriminer la dimension de base et la dimension de puissance.

Dans la plupart des systèmes 1x1D, les deux dimensions sont facilement séparables de façon externe : chacune des deux dimension est représentée par un moyen différent (forme et position pour le système arabe, quantité et forme pour le système égyptien). Mais ce n’est pas le cas de toutes. Ainsi, dans le système de numération grec, la dimension de base et la dimension de puissance sont représentées par la forme, la possibilité de discriminer ce qui code l’une ou l’autre de ces dimensions devient interne : c’est par une opération mentale requérant la mémoire qu’on peut séparer base et puissance d’une représentation numérique.

Ainsi, pour le nombre $\tau$ (tau) signifiant 300, on ne peut pas séparer le 3 du 100 ; pour le nombre $\lambda$ (lambda) signifiant 30, on ne peut pas séparer le 3 du 10 ; et il n’y a rien de semblable entre $\tau$ et $\lambda$ alors qu’ils partagent tous les deux la même valeur de base. Il est évident que cette particularité rend le système de numération grec plus exigeant en ressources cognitives puisque ni la dimension de base, ni la dimension de puissance, ni même la façon dont on peut discriminer ces deux dimensions ne possèdent d’indices externes.

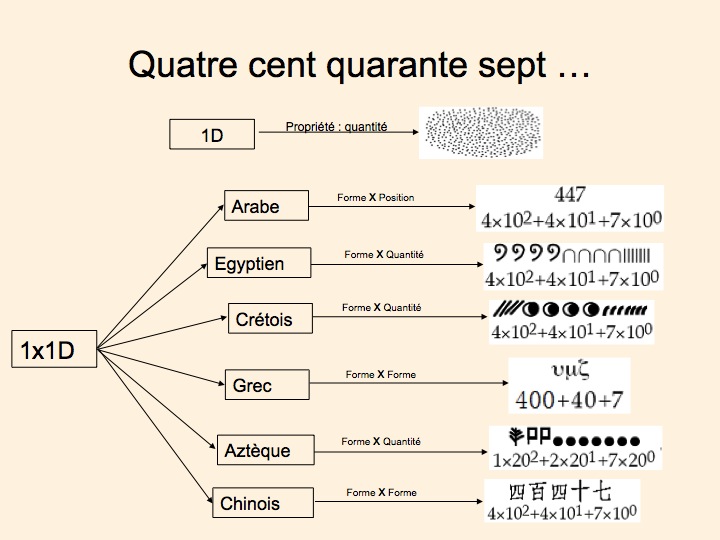
Reprenons notre 447 pour voir comment il s’écrit dans ces différents systèmes :

• • En arabe, le nombre quatre cent quarante sept s’écrit donc 447, soit $4\times 10^2+4\times 10^1+7\times 10^0$.
  • En égyptien, le nombre quatre cent quarante sept s’écrit : 4 fois la quantité cent plus quatre fois la quantité dix plus sept fois la quantité un.
  • En crétois, c’est la même chose, seuls les symboles différent (pour le système aztèque, c’est pareil mais avec la base 20).
  • Les systèmes grec et chinois codent la base et la puissance par la forme, ils sont tous les deux en base 10 mais pourtant ils n’écrivent pas 447 avec le même nombre de caractères. C’est parce que dans le système chinois, il n’y a qu’un signe pour représenter chaque puissance de 10 contrairement au grec. Cela facilite l’apprentissage et le traitement de l’information car le nombre de signes est plus réduit, par contre, cela alourdit la notation puisqu’il faut chaque fois deux signes pour coder les puissances de 10 (le facteur et la puissance).

Systèmes (1x1)x1D

Il existe enfin des systèmes qui reposent sur trois dimensions. Ce sont en fait des systèmes à deux dimensions, comme les précédents, dont l’une se décompose en deux sous-dimensions.
Au premier niveau, on a une dimension de base principale et une dimension de puissance principale. La dimension de base principale se décompose en une dimension de sous-base et une dimension de sous-puissance. Les numérations babylonienne, maya et romaine sont des exemples de ce type de système.

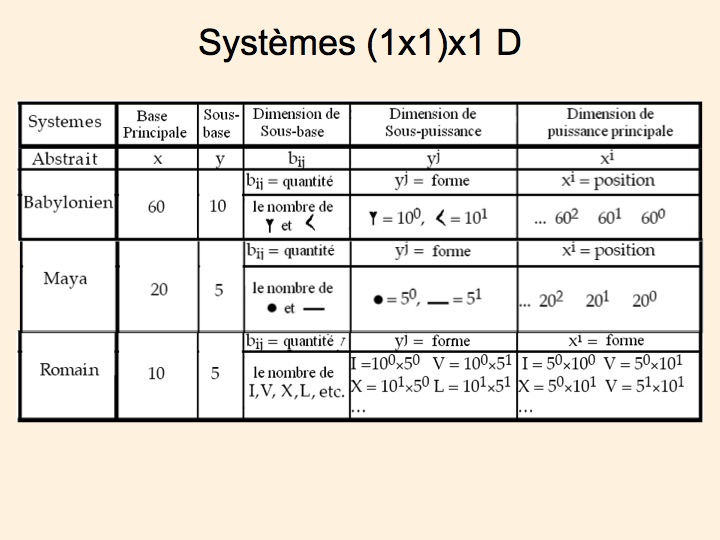
– Pour illustrer le fonctionnement d’une numération (1x1)x1D, on va se pencher sur le fonctionnement du système babylonien. Dans ce système, la dimension de base principale « est en base » 60. Elle se décompose donc en

• • une dimension de sous-base en base 10 représentée par la quantité
  • et une dimension de sous-puissance représentée par la forme (le clou pour $10^0$ et le chevron pour $10^1$).
    Avec ces deux sous-dimensions, on représente les nombres de 1 à 60, ce que requiert la base principale. La dimension de puissance principale, quand à elle, est représentée par la position. À chaque puissance de 60, il y a un décalage de position (position 0 pour $60^0$, position 1 pour $60^1$, etc.).

– Le système maya fonctionne sur le même principe, mais les bases principale et secondaire sont respectivement de 20 et 5 :

• • la dimension de sous-base en base 5 représentée par la quantité
  • et une dimension de sous-puissance représentée par la forme (le point pour $5^0$ et le trait pour $5^1$).
    La dimension de puissance principale est aussi représentée par la position.

– Plus familier pour nous, le système romain fonctionne sur le même principe, mais il est passablement plus compliqué puisque les deux dimensions de puissance sont portées par la même propriété : la forme. La dimension de base principale est en base 10. La dimension de sous-base est en base 5 et elle est représentée par la quantité ; la dimension de sous-puissance est représentée par la forme (I et V, X et L, C et D, etc.) La dimension de puissance principale est aussi représentée par la forme (I et V pour $10^0$, X et L pour $10^1$, C et D pour $10^2$, etc.). Sur le plan historique, on peut noter que la dimension de sous-base (qui est représentée à l’origine par la quantité des signes) s’est perfectionnée tardivement pour intégrer une composante de position : IV pour IIII ; XL pour XXXX, etc.

Voici comment on écrit 447 dans ces trois systèmes :

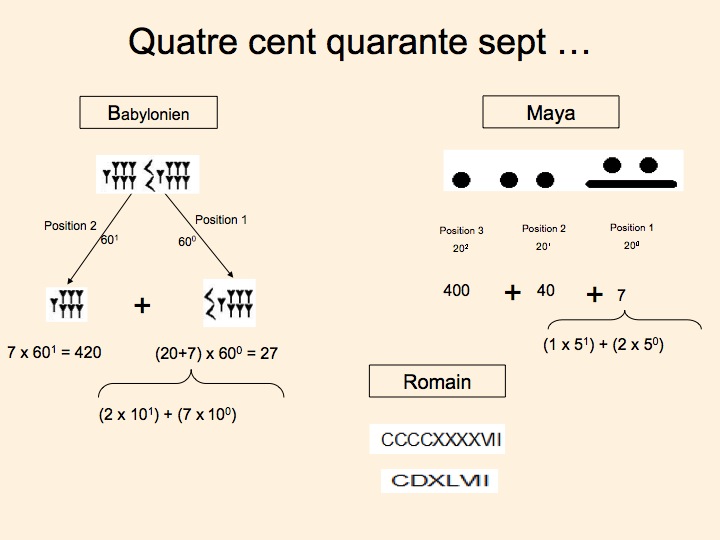
À noter que les propriétés de quantité et de position, quand elles sont utilisées ensemble, peuvent occasionner des ambiguïtés dans l’écriture (l’espace entre deux symboles identiques sur la même puissance de la base diffère peu de l’espace entre deux symboles identiques sur deux puissance différentes).

Récapitulons les différentes façons de noter le même nombre :

On voit que la pluralité des formes peut conduire à des expressions très différentes les unes des autres. Les notations arabe et grecque pourraient être considérées comme assez proches, dans la mesure ou elle ne comportent l’une et l’autre, que trois signes pour coder le nombre quatre cent quarante sept. Pourtant, comme on l’a vu, le fait que les dimensions de base et de puissance du système grec soient codées toutes les deux par la forme le rend bien moins efficace que le système arabe.

Une fois que cette taxonomie est posée, nous allons voir comment elle peut offrir un cadre de compréhension à propos de la façon dont on parvient à se représenter les nombres.
Pour introduire cette nouvelle partie, il faut revenir un tout petit peu sur l’arrière plan scientifique qui sous-tend ce travail sur les représentations des systèmes de numération. De nombreux travaux de psychologie consacrés à l’étude du raisonnement ont montré depuis longtemps que des problèmes « isomorphes » peuvent être plus ou moins difficiles à résoudre en fonction de leur « habillage ». Des problèmes isomorphes, sont des problèmes identiques du point de vue formel : ils comportent le même nombre d’objets, ces objets ont les mêmes propriétés, ils entretiennent les mêmes relations logiques les uns avec les autres, et ces problèmes requièrent les mêmes opérations pour atteindre le but. La seule chose qui diffère entre des problèmes isomorphes, c’est la présentation, la petite histoire avec laquelle on habille le problème. Une différence qui n’a aucune pertinence du point de vue des opérations à mettre en œuvre pour résoudre le problème.

Par exemple, le problème de la Tour de Hanoï est bien plus facile que celui des Boîtes de Saigon, alors que ce sont des isomorphes absolus, et cette différence est due au fait que les règles sont supportées par des indices externes dans le cas de la Tour de Hanoï, alors qu’il est nécessaire de les activer mentalement (interne) pour les Boîtes de Saigon.

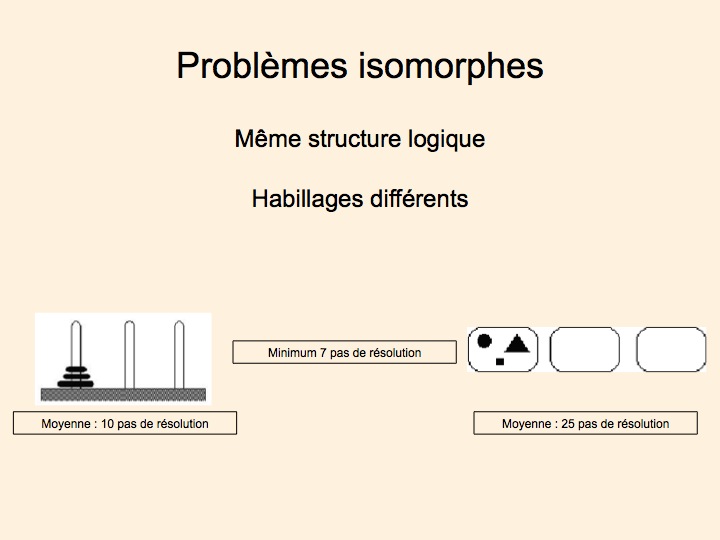
Cette notion de problèmes isomorphes est facilement transférable au niveau des différents systèmes de numération. Et on va voir qu’elle offre un cadre conceptuel original pour interpréter les différences entre systèmes de numération.

De fait, on peut dire que tous les systèmes de numération sont isomorphes car ils représentent tous la même chose : des nombres, mais ils les représentent sous des atours différents.

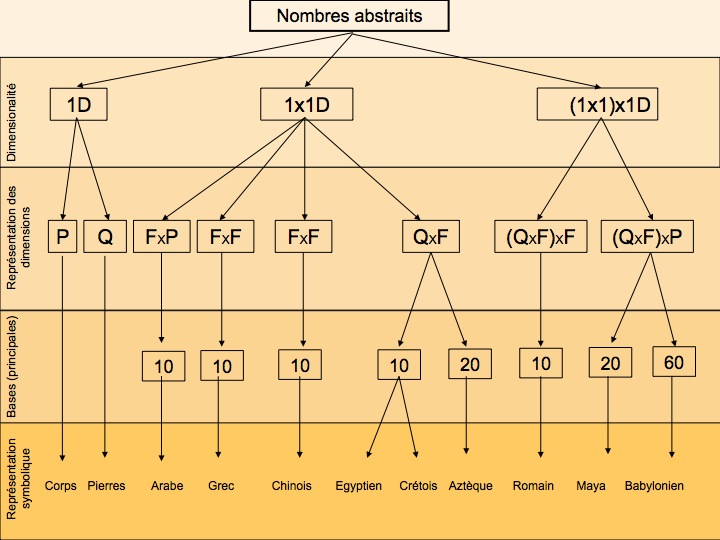
1. Au premier niveau d’habillage, les systèmes de numération peuvent différer par leur dimensionnalité. On a vu trois types de dimensionnalité : 1D ; 1x1D ; (1x1)x1D pour rendre compte des nombres. Ce niveau affecte principalement l’efficacité du codage de l’information. Les systèmes 1D sont linéaires, alors que les autres sont polynomiaux ; l’encodage de l’information est plus économique en termes de nombre de symboles. Particulièrement bien adaptés aux petites quantités, les systèmes linéaires exigent de mobiliser de lourdes ressources attentionnelles dès que les nombres figurés dépassent la dizaine (il faut pouvoir discriminer tous les points, il faut une stratégie de comptage pour être sûr de tous les avoir, etc.).

2. À un deuxième niveau, des systèmes isomorphes du point de vue de leur dimensionnalité, peuvent différer au niveau de la représentation des dimensions, c’est-à-dire au niveau des propriétés utilisées pour représenter les dimensions de base et de puissance. Ces propriétés sont le plus souvent la quantité, la forme et la position. Comme on l’a vu, ce niveau est très important pour la construction de la représentation puisque les différentes propriétés n’offrent pas les mêmes indices externes. Quantité et position sont externes alors que la forme nécessite un codage interne.

3. Le troisième niveau est celui des bases. Là encore, des systèmes isomorphes sur les niveaux précédents, peuvent différer. Ainsi, les systèmes égyptien et aztèque, qui sont tous les deux des systèmes 1x1D, dont la base est codée par la quantité et la puissance par la forme, diffèrent sur la valeur de leurs bases (respectivement 10 et 20). Il est évident que ce niveau des bases a une influence sur la facilité avec laquelle on peut se représenter les nombres. Plus la base est importante, plus elle sera difficile à gérer mentalement. Si la base est portée par la propriété « quantité », comme dans les systèmes égyptien et aztèque pris en exemple, on peut discriminer sans effort // de /// par une perception visuelle directe ; cela sera plus difficile pour //// et ///// mais cela deviendra franchement scabreux pour le couple ///////////////// et //////////////////. Bref, dès qu’il devient nécessaire de compter les signes pour atteindre le nombre signifié, la représentation du nombre devient difficile à construire.

Par ailleurs, les bases importantes (60 pour le babylonien) sont très compliquées à manipuler directement :

• • si on code la base à l’aide de la forme, il faudrait construire 60 signes distincts pour la manipuler (difficulté de faire un système de signes à la fois distincts les uns des autres et simples à construire — imaginons qu’on doive poursuivre après notre 9 pour faire 51 autres chiffres...) ;
  • si on la code à l’aide de la quantité, elle serait infernale, absolument pas ergonomique (on a vu la galère pour dénombrer immédiatement des ensembles de taille moyenne ; au-delà de cinq, cela n’est pas évident, ; au-delà de dix, cela devient franchement scabreux, et il faut recourir au comptage).
    La base 60, comme la base 20, impose donc une décomposition en sous-base et sous-puissance pour être viable.

Ce niveau des bases est extrêmement important sur le plan strictement mathématique. Je ne sais pas s’il existe un système de numération naturel qui fonctionne en base 12, mais, même sans être mathématicien, on conçoit que le fait que 12 soit divisible par 12, 6, 4, 3, 2 et 1 (6 valeurs) lui donne un avantage certain, en termes de calculs, sur 10 qui n’est divisible que par 10, 5, 2 et 1. En extrapolant, on peut subodorer les vertiges occasionnés par une arithmétique basée sur 60, super divisible (10 valeurs), ou une autre basée sur un nombre premier.

4. Le dernier niveau est celui de la représentation symbolique. La graphie utilisée pour coder peut différer alors même que tous les niveaux supérieurs sont identiques. Ce niveau peut affecter la facilité d’écriture et de lecture des nombres, ce qui entraîne des conséquences au niveau de leur apprentissage, de leur utilisation et de leur diffusion.

Cette organisation hiérarchique en quatre niveaux d’isomorphie, construite sur l’observation de 11 systèmes de numération dans le cas présent, est en réalité complètement ouverte : tous les systèmes de numération existants peuvent se décomposer selon les principes exposés ici, et cette organisation peut même servir de matrice pour en générer un grand nombre d’autres (rien qu’en laissant ouvert le nombre de propriétés sur lesquelles peuvent s’appuyer les dimensions de base et de puissance — couleur, hauteur, taille des signes, etc. — et le nombre de base). Quand à savoir si cela pourrait offrir des perspectives originales en termes de mathématiques, je suis moins bien placé que vous pour en juger.

Pour finir, on va s’interroger sur les atouts véritables du système de numération arabe.
Certes, c’est un système remarquablement bien conçu. Très peu de choses à travers le monde sont aussi universelles que la numération arabe (langues différentes, écritures différentes). On invoque très souvent la propriété de position qui permet de coder les puissances de la base pour justifier cette prédominance. Certes, c’est une invention maligne, qui offre l’indéniable avantage d’ouvrir à l’infini les possibilités de noter des valeurs de plus en plus grandes.
Mais on peut se demander si cette unique propriété de position suffit à justifier la prééminence de la numération arabe. D’ailleurs, à partir du million, il devient nécessaire de recourir à un autre type de notation, les puissances de 10 se codant en incrémentant la valeur de l’exposant plutôt qu’en occupant une nouvelle place. Sans cette méthode, le dénombrement des positions devient aussi scabreux que le dénombrement simple d’objets dans un système 1D.

Par ailleurs, le système arabe n’est pas le seul à utiliser cette ficelle, les systèmes babylonien et maya l’utilisent aussi, de même que les abaques, les tables de calculs, les kipus péruviens (systèmes de nœuds sur des cordelettes), etc.

Alors, qu’est-ce qui rend le système arabe si particulier ? On va faire un résumé rapide de ses différents atouts.

Au niveau de la dimensionnalité, c’est un système 1x1D. Ce qui le rend plus efficace que les systèmes 1D pour encoder l’information numérique (comparer 447 en 1D et 1x1D). Par ailleurs, pour ce qui est du codage de l’information, les systèmes à 1x1D ne sont pas moins efficaces que les systèmes à (1x1)x1D ; la troisième dimension induit une complexité de traitement sans apporter de gain réel.

Au niveau de la représentation des dimensions, les propriétés de forme et de position peuvent être discriminées de façon externe, ce qui facilité la représentation, au contraire du système grec par exemple. Et la propriété de position, comme on l’a vu, permet d’appréhender de façon externe de très grandes valeurs.

Si on s’arrête à ces propriétés de base et de puissance, on est obligé de reconnaître que les abaques (bouliers), dans lesquels les dimensions de base (quantité) et de puissance (position) sont toutes les deux externes et discriminables l’une de l’autre, sont aussi efficaces pour la représentation d’une valeur numérique. Elles sont en outre supérieures à tous les systèmes de numération écrits pour les calculs simples comme les additions ou les soustractions.

Mais si on considère d’autres facteurs, comme la facilité de lecture et d’écriture, ou encore, la possibilité de conserver la trace d’un nombre représenté, le système arabe est supérieur : après un apprentissage raisonnable, les 9 plus 1 symboles peuvent facilement être lus et écrits.

Au niveau des bases, la base 10 est assez grande pour ne pas monter trop vite en régime, et suffisamment petite pour rester facilement manipulable mentalement. Une base plus importante requiert plus de symboles à mémoriser (ou une décomposition en sous-base et sous-puissance), dans les deux cas cela complexifie la manipulation, par contre plus la base est grande, plus elle est efficace pour encoder les grands nombres.

Un autre avantage d’une base pas trop importante, c’est que les tables d’addition et de multiplication, nécessaires à mémoriser pour pouvoir calculer efficacement, sont bien plus petites en base 10 (90 égalités à mémoriser pour les tables de multiplication) qu’en base 20 (système maya : 380 égalités à mémoriser) ou qu’en base 60 (système babylonien : 3540 égalités à mémoriser).

Au niveau des symboles, la graphie utilisée dans le système arabe est simple, bien plus que celle utilisée par les Chinois ou les Mayas, par exemple, ce qui rend son utilisation quotidienne extrêmement facile et rapide.

La combinaison adoptée par le système arabe, à travers ces quatre dimensions, en fait un système très efficace en termes de représentation des nombres. Pour ce qui est des calculs simples, si le système arabe est effectivement plus pratique que le grec, le romain ou l’égyptien, il reste nettement derrière les systèmes d’abaques qui ont été utilisés jusqu’à l’avènement de l’ordinateur dans beaucoup de pays (Chine, Japon ou Russie, par exemple).

La question reste donc posée : en quoi le système arabe est-il si particulier ? La réponse est peut-être dans l’économie de moyens qu’il permet. En effet, les systèmes de numération ont deux fonctions majeures : représentation des nombres et calculs. Dans de nombreuses cultures, ces deux fonctions étaient assurées par des systèmes différents. En Chine par exemple, le calcul se faisait en utilisant le boulier ou des bâtonnets, alors que la représentation se faisait par écrit ; de la même façon, les Romains calculaient en utilisant une table à calcul et notaient les valeurs par écrit. L’intégration de ces deux fonctions de représentation et de calcul dans un seul et même outil, lequel peut être mis en œuvre sans autres moyens qu’un papier et un stylo est sans conteste une réussite sur le plan des contraintes cognitives et technologiques.

Référence : J. Zhang, D. A. Norman, A representational analysis of numeration systems, Cognition 57 (1995), 271-295.