On a vu dans l’article précédent que si $A$ et $B$ sont deux points gaussiens, le vecteur $\overrightarrow{AB}$ est aussi gaussien. Mais sa norme n’est pas gaussienne, ni le quotient de ses coordonnées (le coefficient directeur de la droite $(AB)$).
Norme d’un vecteur
1) Norme d’un vecteur d’espérance $\vec{0}$
Si un vecteur est gaussien d’espérance nulle, la distribution du carré de sa norme est une loi du khi-deux à deux degrés de liberté, et donc sa norme suit une loi de Rayleigh. Pour l’illustrer ainsi que les exemples suivants de cet article, on va renoncer à l’aspect dynamique de CaRMetal pour utiliser la puissance d’Euler Math Toolbox qui peut en une ou deux secondes créer un échantillon d’un million de vecteurs gaussiens ou uniformes [1]... Ainsi les histogrammes seront plus réguliers grâce à la loi des grands nombres.
x=normal(1,1000000); y=normal(1,1000000);permet de créer 1 000 000 nombres aléaoires gaussiens centrés réduits (stockés dans une matrice $x$) et 1 000 000 autres stockés dans $y$. Le vecteur de coordonnées $(x ;y)$ est donc gaussien d’espérance $(0 ;0)$. Sa norme est obtenue par
sqrt(x^2+y^2);mais c’est encore une matrice ligne d’un million de données. On n’a donc plus qu’à afficher la répartition des échantillons selon leur valeur (autrement dit, l’histogramme) pour voir à quoi ressemble la fameuse loi de Rayleigh), dans le cas présent avec 100 rectangles :
plot2d(d,distribution=100);EuMathT produit en moins de 2 secondes le beau graphique suivant :
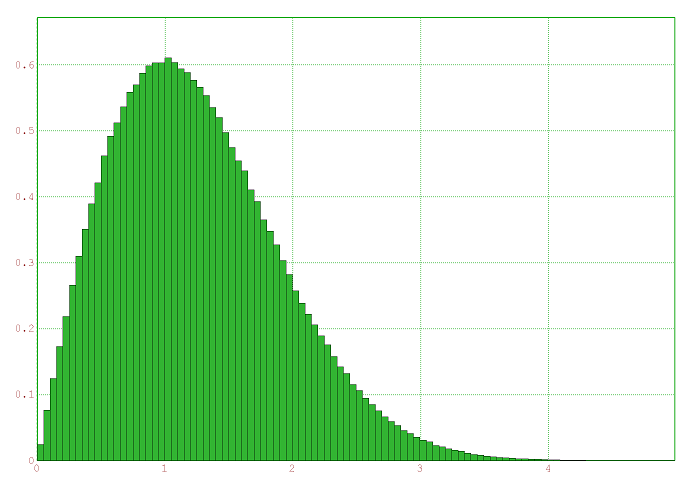
2) Norme d’un vecteur d’espérance non nulle
Par analogie avec ce TP de Seconde, on va considérer le cas où le vecteur a pour espérance $\left(\frac{7}{2} ;\frac{3}{2} \right)$. Le code EuMathT ressemble alors à ceci :
x=3.5*ones(1,1000000)+normal(1,1000000); y=1.5*ones(1,1000000)+normal(1,1000000);
d=sqrt(x^2+y^2);
plot2d(d,distribution=100);et le graphique obtenu
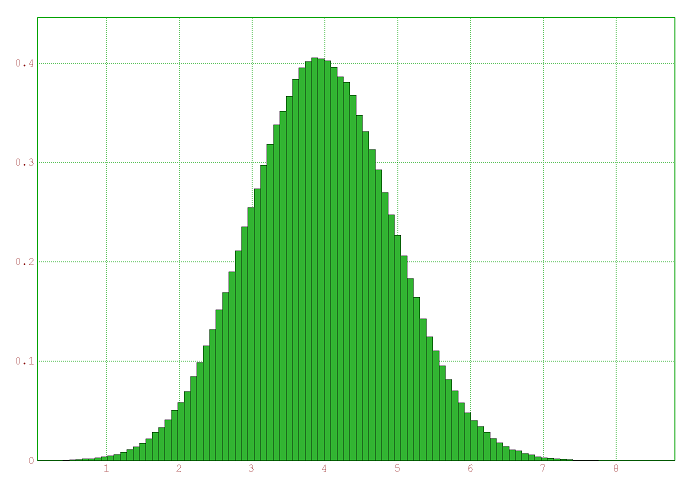
montre que la distribution des normes, si elle n’est pas gaussienne, est presque gaussienne...
3)Norme d’un vecteur uniforme
Le corrigé de ce TP montre que la distribution de la norme d’un vecteur dont l’abscisse est uniforme sur $\left[3 ;4\right]$ et l’ordonnée est uniforme sur $\left[1 ;2\right]$ est assez compliquée. Voici la version EuMathT :
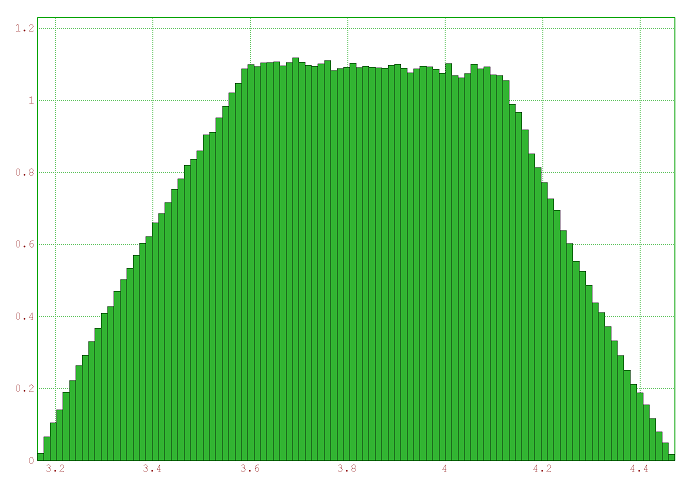
Elle a été obtenue avec ce code :
x=3+random(1,1000000); y=1+random(1,1000000);
d=sqrt(x^2+y^2);
plot2d(d,distribution=100);



Commentaires