Le sujet est téléchargeable ici :
Sous couvert d’un exercice de construction de cercles, les élèves étaient incités à (re)découvrir la notion de distance médiane, et s’ils en avaient le temps, les quartiles. L’enrobage géométrique du problème permet de montrer immédiatement la non unicité de la médiane.
Il a fallu préparer ce TP avec des explications sur les tableaux en JavaScript, et la manière dont JavaScript effectue le tri de ce tableau. Des exemples de réalisations d’élèves sur les tableaux sont visibles ici et ici.
Plusieurs élèves ont carrément réinventé la méthode de dichotomie :
- Le cercle de rayon 1 devrait faire l’affaire, à vue de nez ;
- Visiblement il contient plus de 50 points donc on essaye un rayon plus petit : La moitié soit 0,5 ; pas de chance, cette fois-ci il y a moins de 50 points dedans ;
- Alors on essaye 0,75 pour le rayon : Après deux ou trois essais on voit que ça ne marche pas ;
- Alors on essaye 0,8 : Un peu trop en moyenne ;
- Puis c’est 0,78
- Et même 0,788...
À ce stade la méthode de dichotomie n’est plus applicable puisque les fluctuations d’échantillonnage empêchent de savoir si on a tenté trop ou trop peu : Trop instable.
Beaucoup d’élèves ont essayé d’ajouter la ligne
var distances=new Array();dans la boucle, créant ainsi 100 fois de suite le même tableau. L’un d’entre eux a créé 100 fois le cercle :
Le problème est qu’on a du mal à voir où est le bon cercle dans tout ça...
En désespoir de cause, un élève a commencé à écrire
distances[1]=
distances[2]=
distances[3]=et il est allé jusqu’à 100 !
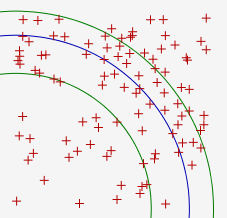
Deux autres ont construit (sans algorithmique) des cercles de rayon variable, et ajusté à la souris leurs rayons pour avoir 25 points dans chaque zone :
Un seul élève a trouvé la construction (pas tout-à-fait exacte) en JavaScript :
var distances=new Array();
o=Point(0,0);
SetHide(o,true);
for(i=1;i<=100;i++){
x=Math.random();
y=Math.random();
p=Point(x,y);
distances[i]=Math.sqrt(x*x+y*y);
}
distances=distances.sort();
c=FixedCircle(o,distances[100/2]);
c=FixedCircle(o,distances[75]);
c=FixedCircle(o,distances[100/4]);
Pour aller plus loin
Le recherche dichotomique des deux élèves citées ci-dessus semble avoir été guidée par le TP précédent : Au début, elle semble converger vers $\frac{\pi}{4}$ qui était justement la réponse du TP sur la méthode de Monte-Carlo. D’où l’idée de chercher la « vraie médiane » de ce nuage de points aléatoires. Le script suivant d’Euler Math Toolbox donne un élément de réponse, sous la forme d’un histogramme :
medianes=zeros(1,10000);
for i=1 to 10000; medianes[i]=median(sqrt(random(1,100)^2+random(1,100)^2)); end
plot2d(medianes,distribution=40);L’histogramme produit (avec 1000 points) est ici :
On voit que le mode est bel et bien proche de 0,8 et on peut estimer que l’espérance est plutôt inférieure à 0,8. Sans plus.
À titre de comparaison voici pour le même nuage de points que ci-dessus, la distribution des premiers quartiles :
et celle des troisièmes quartiles :
La recherche d’une « médiane théorique » peut se faire « à la Riemann » en transformant l’énoncé probabiliste en énoncé purement géométrique : Trouver le rayon du cercle centré sur l’origine qui partage le carré unité en deux zones de même aire. Plus généralement, trouver trois cercles centrés sur l’origine qui partagent le carré unité en quatre zones de même aire. Sans en dire plus, on constate que le rayon théorique du cercle médian est affectivement assez proche de $\frac{\pi}{4}$ (erreur relative de 1,6 %).
Par ailleurs, en essayant ce TP, on développe l’impression que certains rayons reviennent souvent (essayer de régler à la main les rayons des trois cercles dans la figure ci-dessus).
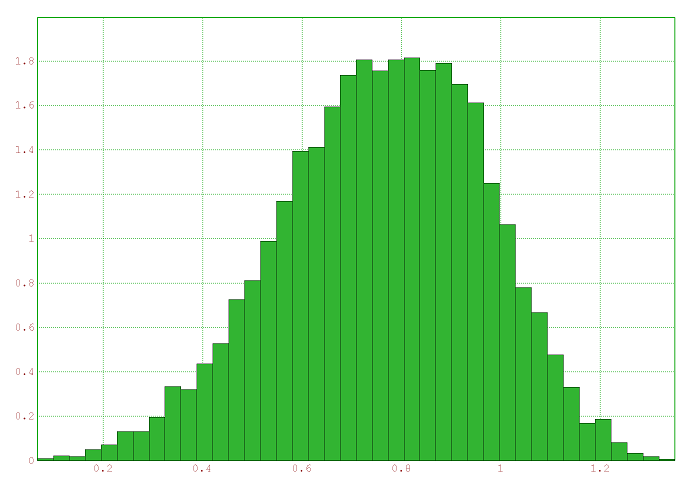
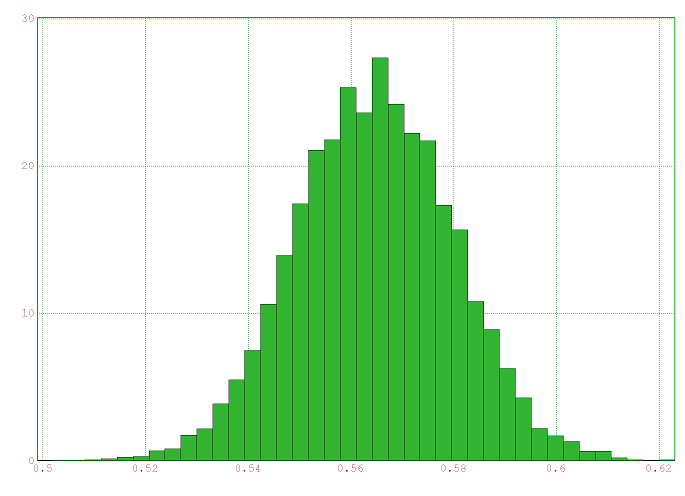
Commentaires