Les auteurs du jeu ont oublié de dire comment ils ont inventé son nom... En tout cas voici la règle du jeu, qui se joue avec un nombre pair de pièces de monnaie, disposées en cercle, en alternant les pile et les face :

À chaque tour, on retourne une pièce qui est encerclée par deux pièces différentes d’elle (face-pile-face ou pile-face-pile). Dans ce cas on retourne aussi les deux pièces voisines. Le but du jeu est d’obtenir le plus grand nombre possible de « pile ».

Blet est donc un casse-tête. On appelle blet-2n le jeu avec 2n pièces. Au bas de cette page on peut télécharger les jeux à 4, 6, 8, 10 ou 12 pièces, mais voici les jeux à 4, 6 ou 8 pièces, jouables en ligne (pour lancer le jeu, utiliser le script en haut à gauche, et pour retourner une pièce, cliquer en son centre) :

Il est clair que pour blet-4 on ne peut pas se débarasser de la dernière pièce qui est sur « face ». On essaye toutes les possibilités, et aucune ne permet de dépasser les 3 « pile ». Ce phénomène est d’ailleurs général, puisque le dernier coup ne peut être que le passage de « face-pile-face » à « pile-face-pile » qui laisse un « face »...

Dans blet-6 par exemple, on ne peut pas dépasser les 5 « pile ». En fait, en essayant toutes les possibilités, on n’arrive même pas à dépasser les 4 « pile » !

La théorie du jeu consiste donc à déterminer, en fonction de n, le nombre maximal de « pile » qu’on peut obtenir à blet-2n, c’est-à-dire le nombre de « pile » à partir duquel on considère le jeu comme gagné. Pour ce faire, les inventeurs du jeu ont utilisé des calculs d’angle !

Pour une implémentation sur ordinateur telle que celle de GtkBoard, il est commode de dérouler le cercle des pièces en écrivant une suite de P et de F. Alors le jeu blet peut être considéré comme une sorte de grammaire formelle, avec les règles de transformation suivantes :

$$PFP \rightarrow FPF$$

$$FPF \rightarrow PFP$$

Ces règles de transformation évoquent fortement la principale relation de la théorie des tresses fondée il y a une centaine d’années par Emil Artin... La « grammaire » évoquée ici n’est pas un langage rationnel pour autant, parce qu’après la dernière lettre (prise dans l’alphabet $\left\{P,F \right\}$) se trouve la première lettre à nouveau...

Il est vraisemblable que le jeu blet ait trouvé sa genèse dans ces considérations de grammaires transformationnelles.

Pour déterminer le minimum du nombre de « face » restant à la fin du jeu, ses créateurs utilisent la géométrie : À chaque mot de 2n lettres formé de P et de F ils associent deux chemins, l’un représenté en bleu, l’autre en rouge, avec les transformations

$$\left\{\begin{array}{l}x’=x \\ y’=x+y \end{array}\right.$$

pour la lettre P (pour "pile"), et

$$\left\{\begin{array}{l}x’=x-y \\ y’=y \end{array}\right.$$

pour la lettre F (pour "face").

Le chemin bleu commence par (1,0) et le chemin rouge par (0,1) :

Lorsque les chemins reviennent à leur point de départ, on dit que le mot est fermé (exemple : PFPFPFPFPFPF). Dans ce cas, on démontre que les chemins bleu et rouge tournent de 60n degrés. Or chaque fois que le chemin bleu tourne, c’est sur un P et chaque fois que le chemin rouge tourne, c’est sur un F. Et comme à chaque fois, l’angle de rotation est strictement inférieur à 180°, on en déduit que le nombre de P et le nombre de F sont tous les deux strictement supérieurs à $\frac{n}{6}$. Et cette propriété reste vraie pour les mots dont une puissance est « fermée », comme la configuration de départ de blet-2n. Par exemple,

• pour blet-4, l’angle est de 120°, ce qui veut dire au moins une rotation : Au moins un « face » donc au plus 3 « pile » ;
• pour blet-6, l’angle est de 180°, donc il faut au moins 2 « face », soit au plus 4 « pile » ;
• pour blet-8, l’angle est de 240° ce qui nécessite aussi au moins deux « face » soit au plus 6 « pile » ;
• pour blet-10, l’angle de 300° est atteint en au moins 2 rotations aussi, soit encore au moins 2 « face », ou au plus 8 « pile » ;
• et pour blet-12, un tour complet est effectué, ce qui nécessite au moins trois rotations d’angles inférieurs à 180°, donc au moins 3 « face », soit au maximum 9 « pile ».

On récapitule dans le tableau suivant :

SL(2,Z)

Les chemins ci-dessus ont été choisis de manière que les matrices de « pile » et de « face » soient toutes les deux dans $SL(2,\Z)$ (matrices à coefficients entiers, de déterminant 1). Or ces matrices opèrent sur le demi-plan de Poincaré en représentant la matrice $\left(\begin{array}{rr}a & b \\ c & d \end{array}\right)$ par la fonction $z \mapsto \frac{az+b}{cz+d}$. Ci-dessous, on a représenté l’image d’un quadrilatère par cette transformation. On peut déplacer les sommets du quadrilatère avec la souris (ou en cliquant sur le singe) ou déplacer le quadrilatère entier avec la souris :

Cette voie n’a semble-t-il pas été explorée par les créateurs du jeu, et il n’a pas évident de voir si elle mène à quelque chose d’intéressant ou de novateur...

blet16 a été implémenté dans le jeu Enigma :

Le principe consistant à retourner des jetons évoque un célèbre jeu de stratégie (à deux joueurs celui-là) : reversi-Othello.

D’autres jeux utilisent des jetons, parfois juste comme marqueurs pour remplir des tableaux booléens, comme ce jeu qui figurera dans la prochaine version d’Enigma (1.1) :

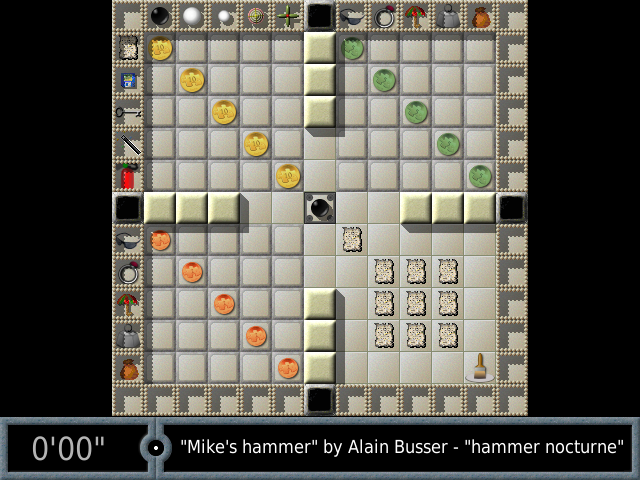
Il s’agit juste d’un jeu de logique style intégramme, où on trouve 5 personnages (M. BouleNoire, M. BouleBlanche, M. Billeblanche etc.), 5 métiers (écrivain, hacker, serrurier etc.) et 5 ustensiles, et où on doit trouver qui fait quoi et qui porte quoi. Très classique, mais au lieu de cocher des cases, on place des pièces dessus.

Enfin les pièces ayant plusieurs valeurs fiduciaires mènent à d’intéressantes questions comme la recherche du nombre de manières de constituer 37 centimes uniquement avec des pièces de 10, 5 ou 2 centimes...