
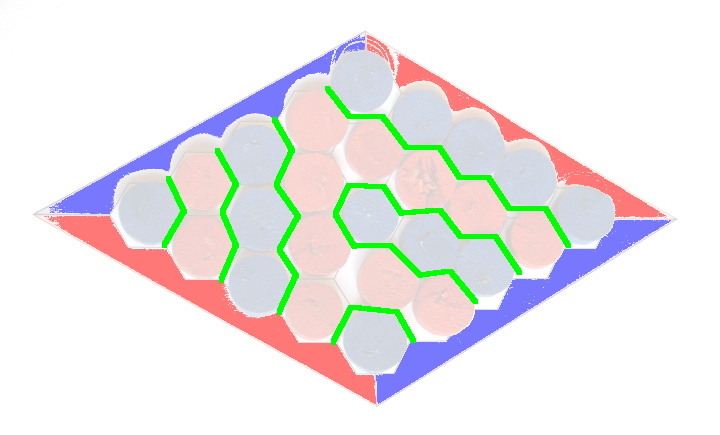
Et c’est le moment de poser la question : qui a gagné ? Cela prend du temps de trouver ! La partie elle-même a duré environ 5 minutes, auxquelles il faut ajouter ce temps. On peut même donner des exercices en distribuant des images similaires à celle ci-dessus et demander qui est le gagnant (par exemple en encerclant les hexagones donnant le chemin gagnant).
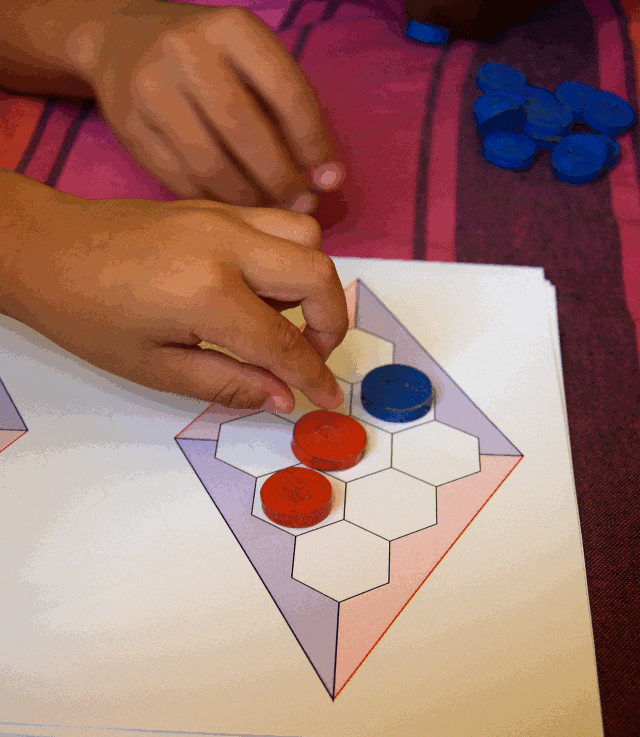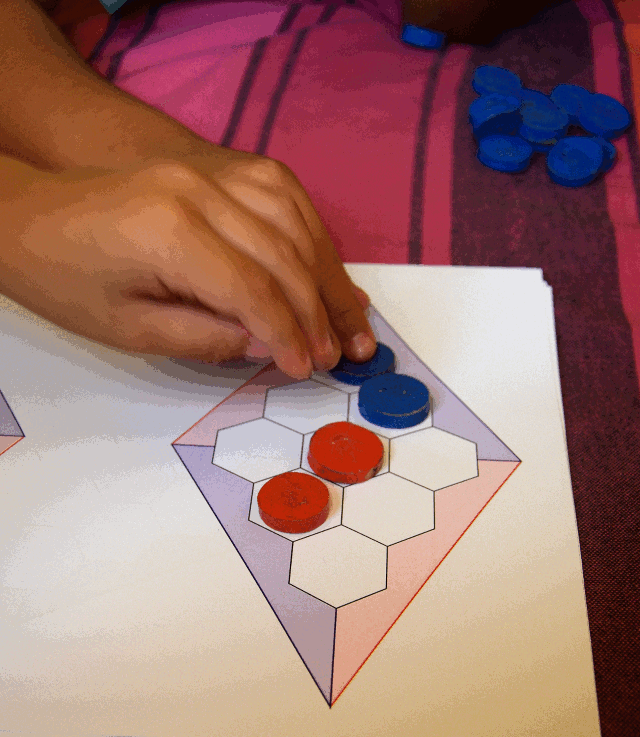
Hex lors de la semaine des mathématiques 2022
Le lundi 28 mars 2022, à l’occasion de la semaine des mathématiques, le jeu de Hex en version coloriage a été pratiqué à l’école Aristide Briand du Tampon (mais pas en cycle 1, ni même en CP pour l’instant).
coloriage
Des élèves (ici en CE 1) colorient avec soin :

Cela permet (ici en CE 1) de voir comment s’est déroulée la partie. Ici il s’est déroulé une vraie course de terrain :
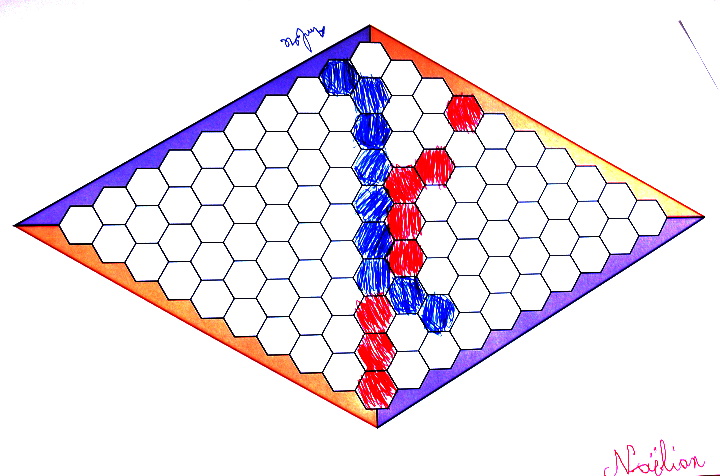
CE 1
Les bleus vont très vite (dessins de cercles au lieu de coloriage) mais se font battre quand même par les rouges, peut-être parce que le chemin est mieux visible lorsque les hexagones sont coloriés :
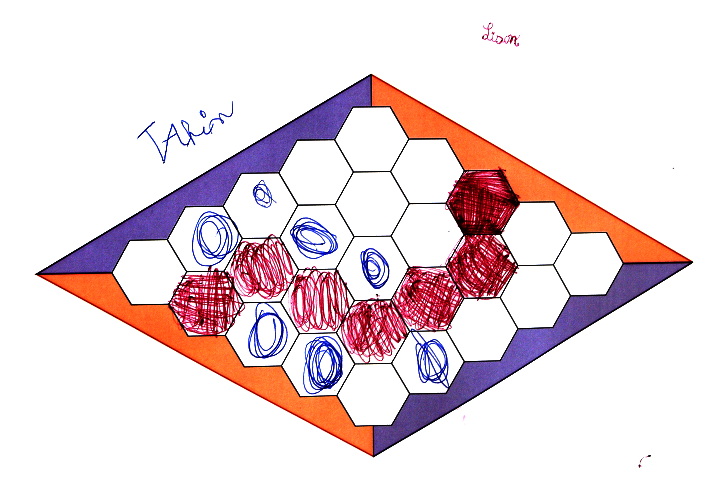
Les bleus gagnent :
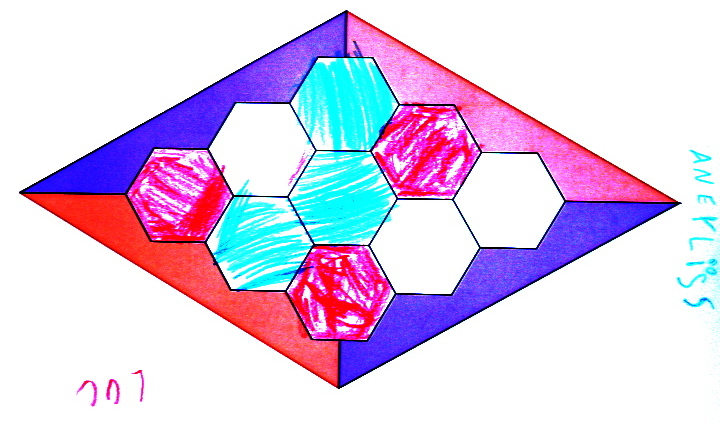
enfin plus précisément les bleus auraient gagné s’ils avaient bien joué : ils auraient dû colorier l’hexagone en face de celui colorié :

De ce fait ce sont les rouges qui ont gagné :
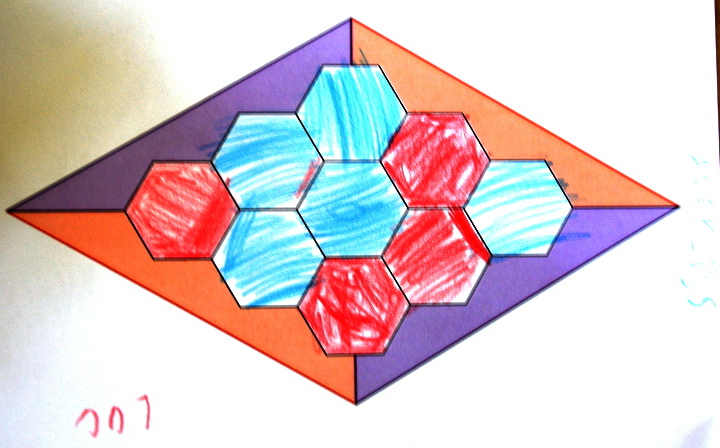
CE 2
Un problème s’est posé dans l’organisation de la journée : les élèves n’étant pas dans leur propre salle, n’avaient pas de crayons de couleur à leur disposition, ils ont donc dû utiliser des feutres :
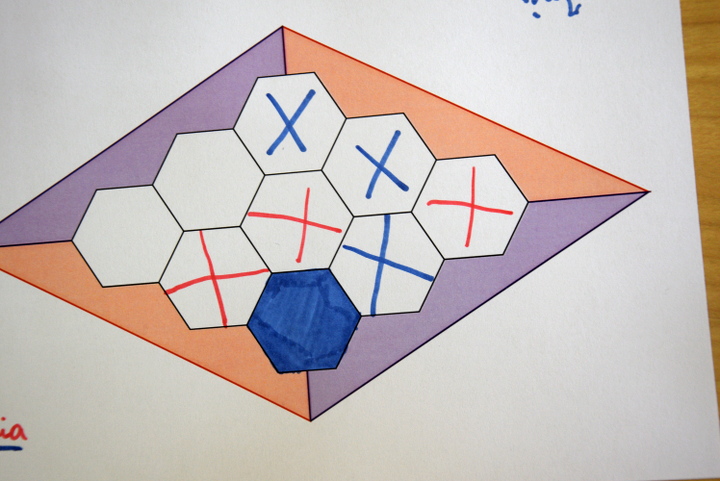
Le risque de vider prématurément la cartouche d’encre du feutre a donc mené les élèves à dessiner de façon plus économique (croix ci-dessus) ce qui a pu nuire à la visibilité des lignes.
Ici les bleus ont perdu, peut-être parce qu’ils essayaient de joindre par un chemin bleu, deux bords de couleurs différentes :
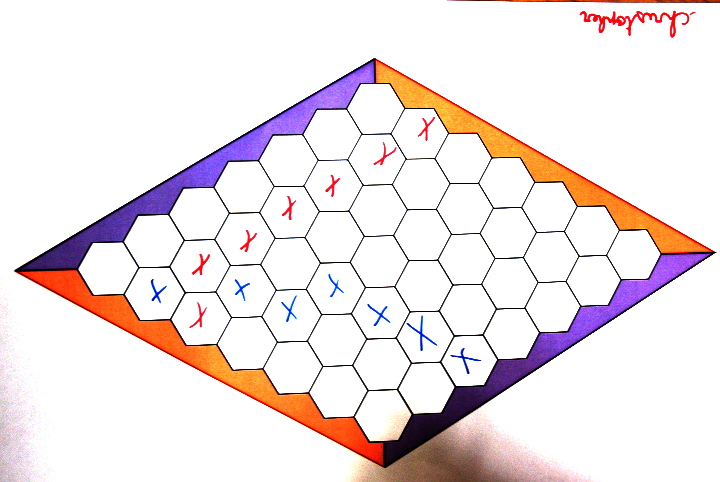
Une situation similaire s’est déroulée ici :
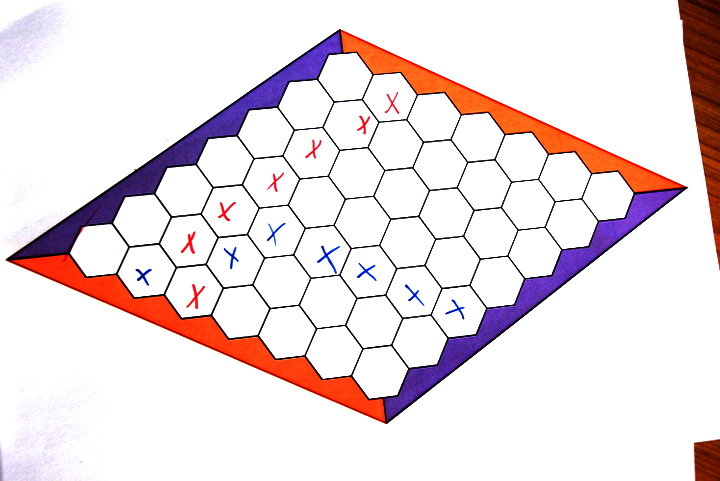
Comme en CE 1, on voit des courses-poursuites :
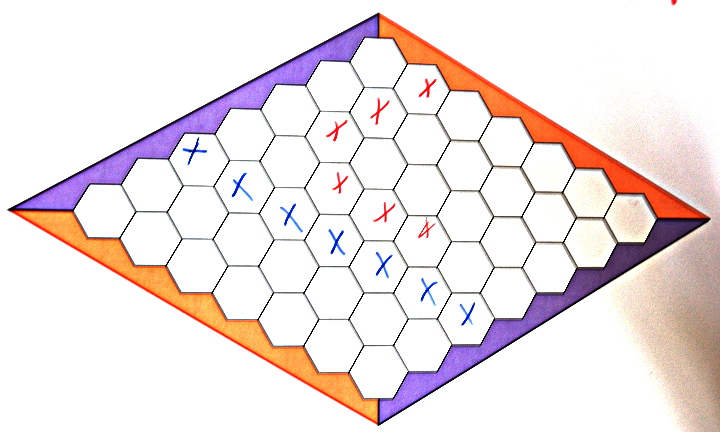
Il est possible que les élèves aient ignoré qu’ils avaient le droit de colorier des cases non contigües. Possible aussi qu’ils n’en aient pas vu l’intérêt.
Ici les bleus ont gagné :

Et ici ce sont les rouges :
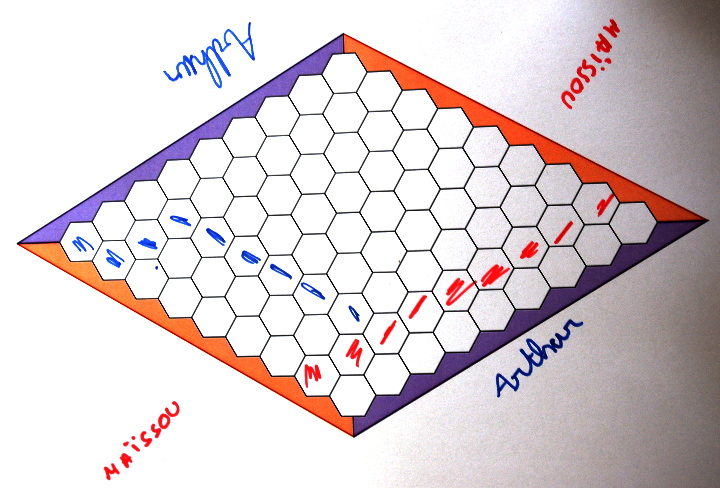
En CE 2, le jeu de Hex consolide des notions de géométrie : hexagone bien entendu, mais aussi le fait qu’un losange est un parallélogramme (chaque joueur a à sa disposition deux bords opposés, donc parallèles, du losange). Pour la jouabilité et pour laisser le temps de réfléchir à une éventuelle stratégie, la version aquarelle aurait sans doute été meilleure, si le temps l’avait permis.
CM 1
En cycle 3, l’activité s’est déroulée à un autre rythme, puisqu’il y a été ajouté la partie sur la machine de Shannon.
Le coloriage a été fait avec plus de soin qu’en cycle 2 :

Les élèves de CM1 ont tendance à ne pas utiliser l’espace blanc pour inscrire leur nom, mais à l’écrire sur chacun de leurs territoires pour les identifier (ici les rouges ont gagné) :

Ici ce sont les bleus qui ont gagné :

La fin de l’activité a consisté à jouer contre la machine, ce qui suppose
- qu’on choisisse où on pose un jeton noir
- qu’on branche sur la machine, un câble noir sur la position choisie
- qu’on mesure les potentiels électriques sur les prises non encore jouées
- qu’on repère la prise de potentiel maximum
- qu’on cherche un chemin gagnant pour les rouges passant par cette prise
- qu’on repère sur ce chemin la prise de potentiel minimum
- qu’on y branche un câble rouge et pose un jeton rouge sur le sommet correspondant.
Le premier groupe a perdu contre la machine (les rouges ont presque un chemin) :

Le second groupe par contre a gagné :

Le point de potentiel maximum est au milieu du bord rouge de gauche :

mais on ne réussit pas à trouver de chemin gagnant pour les rouges passant par ce sommet. En fait il n’existe pas de chemin gagnant pour les rouges, et le fait qu’on ne peut pas appliquer la stratégie des rouges illustre que ceux-ci ont perdu.
Chaque étape nécessite de lire des nombres décimaux sur le voltmètre :

ce qui donne un intérêt nouveau à l’activité (les nombres décimaux sont au programme de cycle 3). Les élèves passent du temps non seulement à lire des nombres décimaux, mais aussi à les comparer (pour savoir où est le maximum ou le minimum).
CM 2
Le coloriage est parfois fait avec beaucoup de soin :

Voici une partie qui vient presque de commencer :
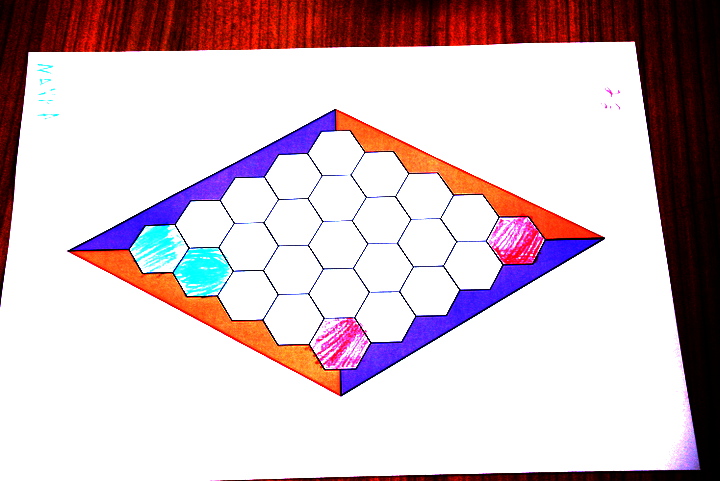
En voyant ce coloriage on se demande si les rouges jouent au mieux :

En fait ils gagnent :

Ici aussi les rouges ont gagné :
La partie sur la mesure de potentiels a plutôt bien marché mais la plupart des élèves n’osent pas manipuler (en cela ils ressemblent déjà à des lycéens).
Une mesure de tension

aboutit à ce que les rouges jouent ce sommet :

Vont-ils gagner ? Nul ne le sait, la séance s’est arrêtée à ce point.
Cycle 3
Voici des extraits du programme auxquels correspond cette activité :
Connaître les unités de la numération décimale (unités simples, dixièmes, centièmes, millièmes) et les relations qui les lient.
Utiliser les nombres décimaux pour rendre compte de mesures de grandeurs.
Connaître le lien entre les unités de numération et les unités de mesure (par exemple
dixième à dm/dg/dL, centième à cm/cg/cL/centimes d’euro).
Comparer, ranger des nombres décimaux.
Ici l’unité de mesure la plus adaptée est le millivolt (mV) qui est le millième d’un volt. Il n’est pas nécessaire que les élèves sachent ce qu’est un volt pour cette activité.
C’est surtout la comparaison des nombres décimaiux qui est mise en œuvre dans cette activité. Par exemple pour trouver le potentiel maximum il faut savoit quelle tension est la plus élevée, entre 2,29V et 2,3V.
énigmes
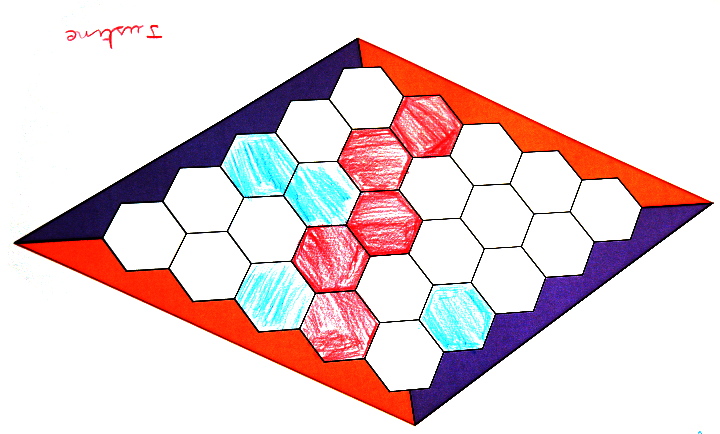
Qui a gagné ce jeu (en CE1) ?
Il y a un hexagone qu’on ne voit pas. Néanmoins on peut savoir qui a gagné ce jeu :

Qui ?
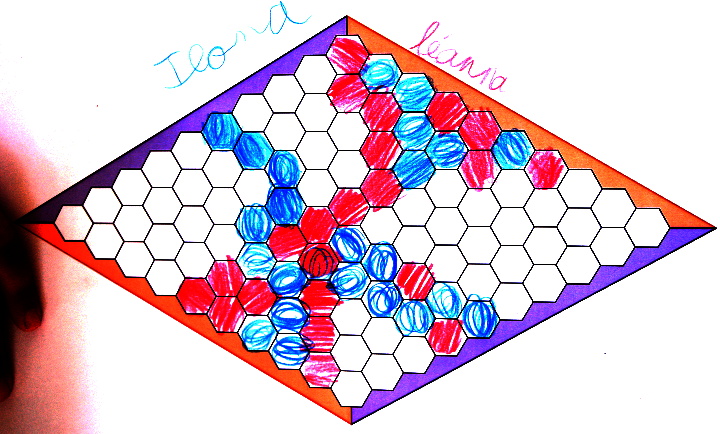
Qu a gagné le jeu ci-dessous (en CE 2) ?
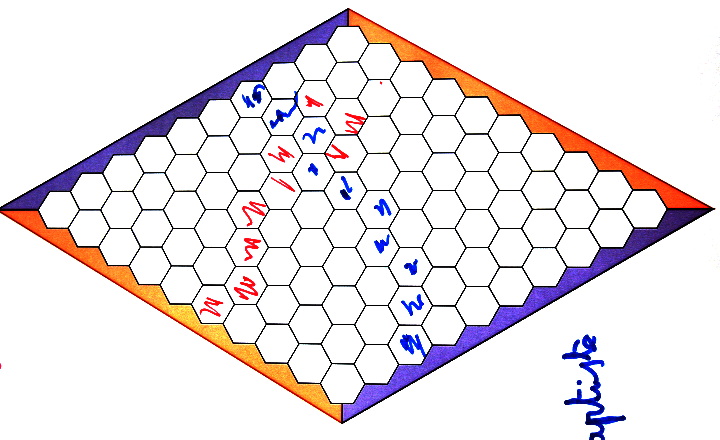
Trois questions à propos de cette partie menée en CM2 :
- qui sera le prochain à colorier un hexagone ?
- qui a joué en premier ?
- qui va gagner cette partie ?
Gouache
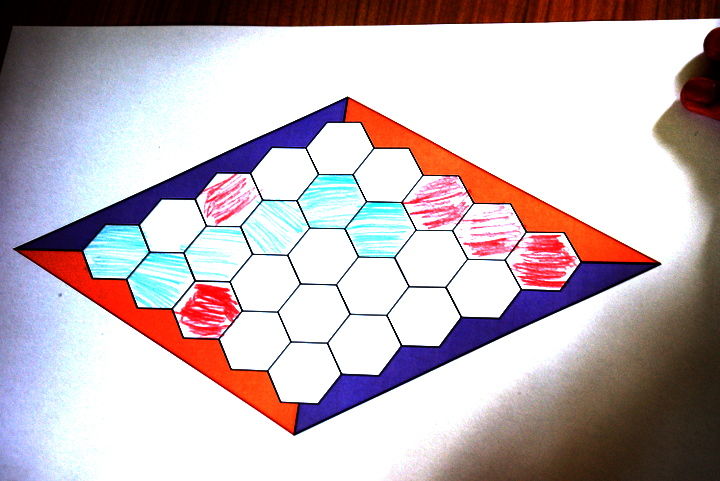
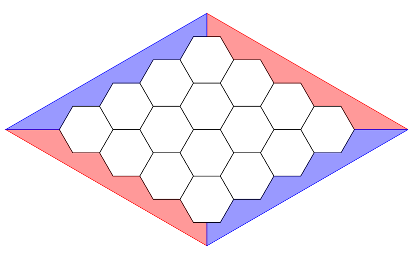
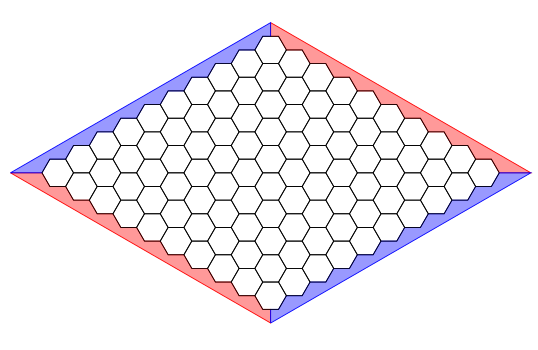
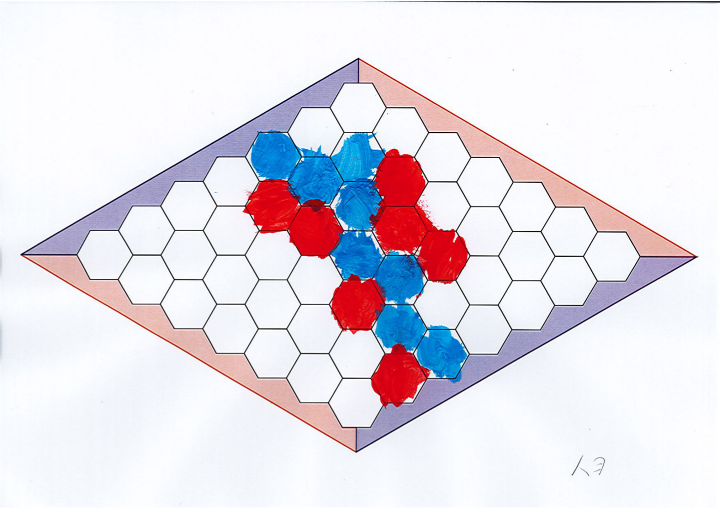
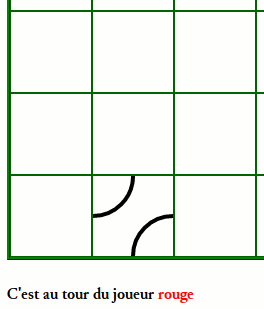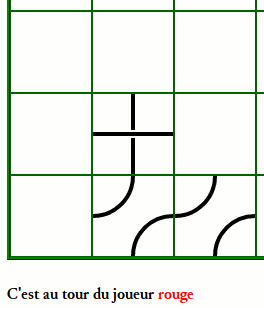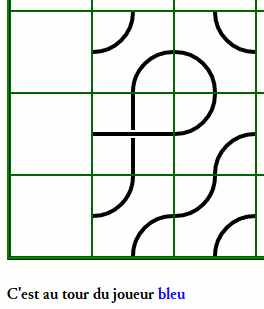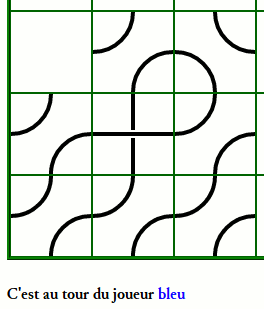
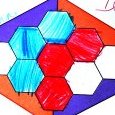
Combien de temps faut-il pour savoir qui a gagné le jeu ci-dessous ?
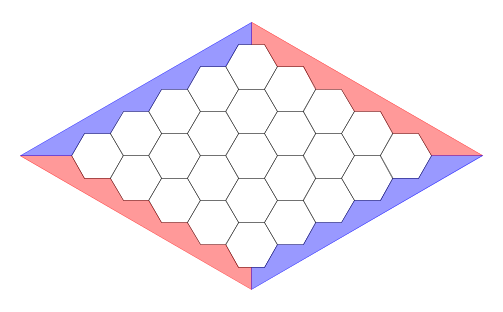
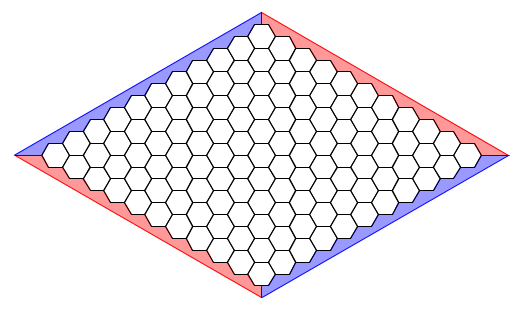
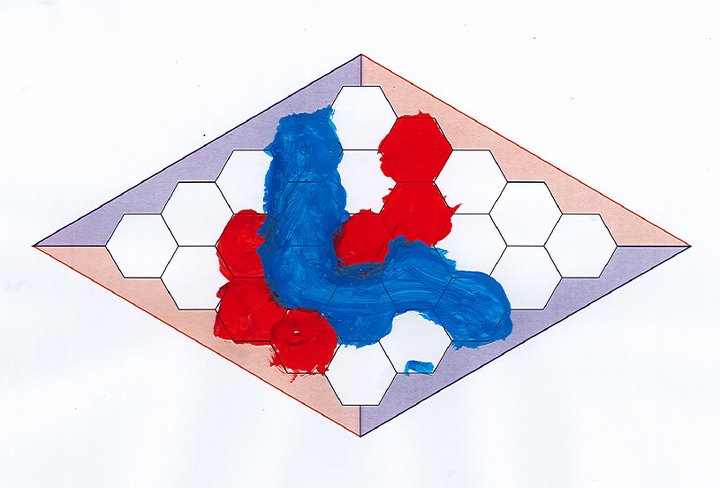
Et pour celui-ci ?
On a pu voir dans les exemples précédents que la perception des chemins est plus facile lorsque les hexagones sont entièrement coloriés. Or pour cela il y a mieux que les crayons de couleur ou les feutres : la gouache. Une technique proche de celle du remplissage à la gouache a ét faite au feutre, en jouant d’abord les bords (intérieurs) puis en les remplissant seulement à la fin de la partie :
L’expérience du jeu de Hex à la gouache a été tentée en CP (classe de CP a de l’école Aristide Briand) le lundi 9 mai 2022. Cela a révélé que le coloriage à la gouache est techniquement plus difficile que celui au crayon, surtout pour ne pas déborder :
Un avantage de la gouache est qu’elle permet de mieux voir les chemins gagnants. Des élèves ont même repassé un coup de pinceau dessus pour convaincre leur adversaire de leur victoire :
Par contre les CP ayant tendance à mettre trop de gouache, les couleurs peuvent se mélanger et faire croire à de la triche.
Remarque : parmi les capacitées attendues en fin de cycle 2 il y a
Agir sur les formes (supports, matériaux, constituants...), sur les couleurs (mélanges, dégradés, contrastes...), sur les matières et les objets : peindre avec des matières épaisses, fluides, sans dessin préalable
Observer, expérimenter des principes d’organisation et de composition plastiques : répétition, alternance, superposition, orientation, concentration, dispersion, quilibre...
On était en plein dedans !
La plupart des élèves de CP ont senti que celui qui joue en premier a plus de chances de gagner. Il leur a alors été demandé comment modifier les règles du jeu de façon à équilibirer les chances. Une élève a proposé cette variante, inédite semble-t-il, du jeu de Hex :
Au début, comme dans le jeu de Hex classique, Bleu colorie (en bleu) un hexagone de son choix. Ensuite, Rouge colorie (en rouge) deux hexagones autres que l’hexagone bleu.
Ensuite le jeu se poursuit normalement, chaque joueur coloriant dans sa couleur un hexagone libre.
Testée en live par les élèves, cette variante semble effectivement moins avantageuse pour le premier joueur, que le jeu de Hex classique. De fait il semble même que maintenant le second joueur soit trop avantagé.
Pour y remédier, une élève a proposé le 4 juillet 2022 une variante de la variante ci-dessus :
Au début, Bleu colorie deux hexagones de son choix.
Ensuite Rouge colorie trois hexagones de son choix.
Après cela, chaque joueur colorie à son tour 1 hexagone comme au jeu de Hex classique.
Cette série de constructions ressemble à une suite de fractions qui pourrait converger vers un nombre quantifiant l’avantage de Bleu sur Rouge à Hex :
- la première fraction (Hex classique) est 1/1=1 : trop petit puisque Bleu gagne
- la seconde fraction (variante du 9 mai) est 2/1=2 : trop grand puisque Rouge gagne
- la troisième fraction (variante du 4 juillet) est 3/2=1,5 qui est entre les deux précédentes.
CP
Le 4 juillet 2022, la classe de CP qui avait déjà eu l’occasion de jouer à Hex avec la gouache, a eu droit à une nouvelle séance, cette fois-ci avec des jetons à deux couleurs :

Aucun n’a essayé d’inventer une variante où on pourrait sous certaines conditions changer la couleur d’un jeton déjà posé (en le retournant). Il faut dire qu’il n’y avait pas assez de jetons pour tous les élèves, et certains nostalgiques de la gouache ont préféré colorier les hexagones au crayon.

Ici les rouges ont gagné mais ils ont joué en premier :
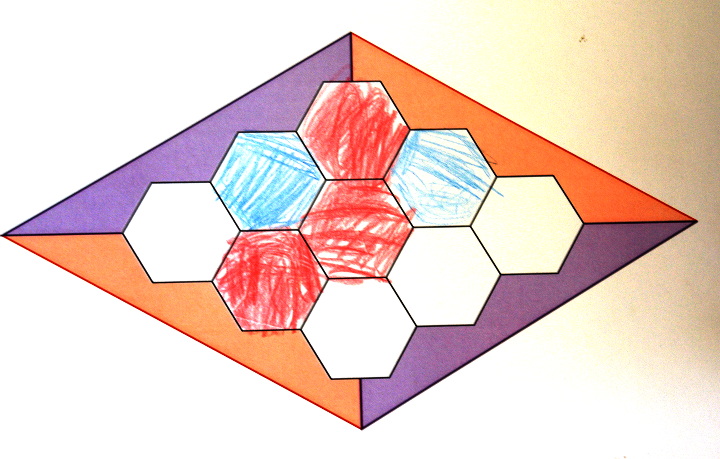
Ici les rouges ne peuvent plus perdre :

Les joueurs semblent en être conscients même s’ils préfèrent continuer le coloriage :
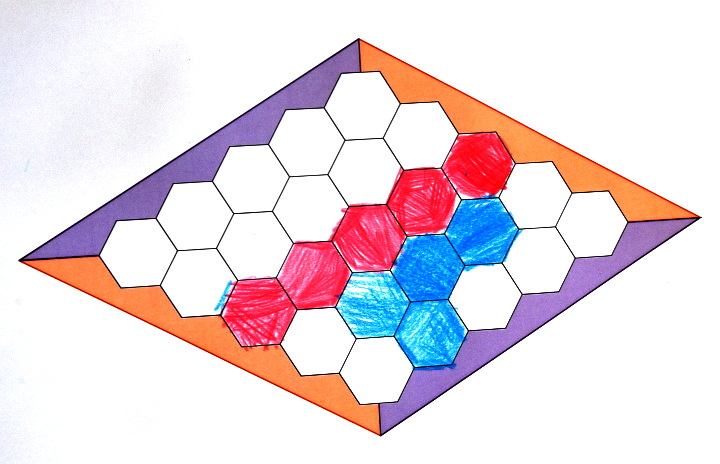
Voici l’analyse d’une partie acharnée au point que les Bleus n’attendaient pas la fin de la coloration de l’hexagone pour contrer :

Les bleus ne colorient pas nécessairement des hexagones contigus, les rouges si :

Malgré ce manque d’anticipation, les rouges finissent en position gagnante (les bleus viennent d’essayer leur progression en haut) :

En fait, on dirait que les bleus ont retenu l’intérêt qu’il y a à colorier en bleu deux hexagones séparés par un « pont » entre deux heaxagones vides, mais n’ont pas encore compris que ça ne sert pas à grand-chose si un des hexagones intermédiaires est déjà rouge. Les rouges gagnent :

Le jeu de Hex est intéressant à jouer à tout âge, car
- dès la petite section, il mobilise la phase de manipulation (placer les jetons au bon endroit, colorier correctement les sommets d’un graphe),
- en grande section (voire avant) il mobilise la perception des lignes (chemin gagnant rouge ou bleu) ce qui pourrait constituer une aide à l’apprentissage de la lecture et du dessin par la suite,
- il pose des questions (cruciales pour beaucoup d’enfants) sur l’équité, et mène à une réflexion intéressante sur la règle du gâteau (en ce sens il contribue à socialiser les élèves),
- une partie de Hex ne dure pas très longtemps (c’est trouver qui a gagné, qui peut être plus long),
- il familiarise avec la structure en nid d’abeille et le fait qu’un losange est un parallélogramme,
- plus tard il permet de réaliser un projet électronique avec la machine de Shannon,
- etc !
Nouveauté 2023 : Hex en moyenne section





































Commentaires