Problème 1 : La base 3 équilibrée
PARTIE I --- Généralités
Question 1
- Voici la traduction décimale des 3 nombres en base 3 équilibrée :
- 1(-1)0(-1)_e = 1 * 33 + -1 * 32 + 0 * 3 - 1 = 27-9-1 = 17
- 1111_e = 1 * 33 + 1 * 32 + 1 * 3 + 1 = 27+9+3+1 = 40
- 1(-1)(-1)(-1)(-1)_e = 34 - 33 - 32 - 3 - 1 = 81-27-9-3-1 = 41
- L’écriture en base 3_e des entiers de 1 à 9 :
| base 10 | base 3_e | Explications |
| 1 | 1 | = 1 |
| 2 | 1(-1) | = 3 - 1 |
| 3 | 10 | = 3 |
| 4 | 11 | = 3 + 1 |
| 5 | 1(-1)(-1) | = 9 - 3 - 1 |
| 6 | 1(-1)0 | = 9 - 3 |
| 7 | 1(-1)1 | = 9 - 3 + 1 |
| 8 | 10(-1) | = 9 - 1 |
| 9 | 100 | = 9 |
Question 2
- Ak = 1 1...1_e = 3k + 3k-1 + ... + 3 + 1 = (3k+1-1)/2 est numérotée 3462 sur OEIS
- Bk = 1(-1)...(-1)_e = 3k - 3k-1 - ... - 3 - 1 = 3k-(3k-1)/2=(3k+1)/2 est la suite 7051 sur OEIS.
Question 3
On modélise par la liste [a_p-1, ... a_1, a_0] le nombre (a_0a_1...a_p-1)_e. Ci-dessous une définition de la fonction valeur(L) qui étant donnée une liste L représentant l’écriture en base 3_e d’un nombre, nous donne sa valeur décimale.
def valeur(L):
return sum(a * 3 ** index for index, a in enumerate(L))Explication du code : ici on utilise une fonction génératrice associée à la fonction prédéfinie sum pour avoir une écriture proche de la formule mathématique : la somme des puissances de 3 fois le coefficient pour tous les coefficients de la liste.
PARTIE II --- Existence et unicité
Question 4
(4a) On suppose qu’un entier n est tel que : n = 3q + r et q s’écrit (a0...ap-1)_e. Dès lors n s’écrit :
- (a0...ap-10)_e si r = 0 ; multiplier q par 3 c’est décaler son écriture vers la gauche et on rajoute 0
- (a0...ap-11)_e si r = 1 ; même chose mais on rajoute 1.
(4b) On suppose que q > 0 et q + 1 s’écrit (b0...bp-1)_e. Dès lors si r = 2, n = 3(q + 1) - 1 et donc s’écrit (b0...bp-1(-1))_e
(4c) On propose une récurrence sur q :
- Initialisation : On a vu au début du sujet que les premiers entiers non nuls possèdent une écriture en base 3 équilibrée.
- Hérédité : On vient de voir comment passer de l’écriture de n à celle de 3n ou 3n+1 (ce qui prouve que ces entiers ont une écriture), et comment on peut passer de l’écriture de 3n+3 à celle de 3n+2. Mais on peut passer de l’écriture de n+1 à celle de 3n+3 ce qui prouve que 3n+3 et 3n+2 ont une écriture.
Question 5
(5a) Définition récursive de incrementeR(L)
def incrementeR(L):
if len(L) == 0:
return [1]
elif L[0] == 0:
return [1] + L[1:]
elif L[0] == -1:
return [0] + L[1:]
else:
return [-1] + incrementeR(L[1:])- Explication de la ligne 9 : On est dans le cas où n = n’ + 1 (L[0] vaut 1) représenté par L. Dès lors [0]+L[1 :] représente n’ et donc L[1 :] seul est un décalage à gauche de n’ et représente n’/3. L’appel récursif représente alors n’/3 + 1 et en redécalant à droite on a 3*(n’/3 + 1) soit n’ + 3 et en ajoutant -1 on obtient n’ + 2 soit n + 1.
- Les lignes 1 et 2 sont là pour le cas terminal : à chaque appel récursif, la longueur de L diminue strictement de 1. En partant d’une liste non vide on finira par tomber sur le cas
len(L) == 0.
(5b) Version itérative :
def incremente(L):
p = len(L)
M = []
k = 0
while k < p and L[k] == 1:
M.append(-1)
k += 1
if k == p:
M.append(-1)
elif L[k] == 0:
M.append(1)
M = M + L[k+1:]
elif L[k] == -1:
M.append(0)
M = M + L[k+1:]
return MQuestion 6
(6a) Si a0, ... , ap-1 sont les chiffres de C, alors C est la somme des ak3k qui sont tous divisibles par 3 sauf ap-1. C et ap-1 ont donc le même reste dans la division euclidienne par 3. Le reste de C est donc égal à ap-1 si celui-ci est positif et à ap-1+3=2 sinon.
(6b) Si a0, ... , ap-1 et b0, ... , bp-1 désignent les écritures de C en base 3 équilibrée, on veut prouver que qk=bk pour toute valeur de k. On peut le faire par récurrence décroissante sur k : D’après la question précédente, on a nécessairement ap-1=bp-1, et on continue la récurrence après divisions successives par 3.
Question 7
def base3e(n):
chiffres = [0,1,-1]
ajout = [0, 0, 1]
L = []
while n > 0:
reste = n % 3
L.append(chiffres[reste])
n = n // 3 + ajout[reste]
return LPARTIE III --- Chemins de Delannoy
Question 8
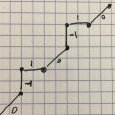
(8a) Chemin de 2019 : 2019 = (10-110-110)_e
(en cliquant sur le chemin de Delannoy ci-dessus, on ouvre une page interactive permettant de voir les chemins de Delannoy des nombres allant de 1 à 800)
(8b) Définir une fonction arrivee(n) qui donne les coordonnées du point d’arrivée du chemin de Delannoy associé à l’entier n.
def arrivee(n):
def add(a, b):
return a[0]+b[0], a[1]+b[1]
steps = [(1,1), (1,0), (0,1)]
ajout = [0, 0, 1]
pt_arr = (0, 0)
while n > 1: # ici 1 pour ne pas prendre en compte le premier chiffre 1
reste = n % 3
pt_arr = add(pt_arr, steps[reste])
n = n // 3 + ajout[reste]
return pt_arrQuestion 9
On considère N(a, b) = { n | arrivee(n) == (a, b) }
(9a) Le min de N(a, a) consiste à avoir le chemin le plus court jusqu’à A(a, a). Donc (10...0)_e Avec a zéros. Ce qui nous donne l’entier 3a. Pour le maximum on va maximiser les puissances de 3... donc (11...1-1...-1)_e (il y a a digits 1 et a digits -1) pour un entier égal à 32a + 32a-1 + ... + 3a - 3a-1 - ... - 3 - 1 =(32a+1-2×3a+1)/2.
(9b) Pour le max N(a, b) avec a < b, ça ne change pas : (11...1-1...-1)_e avec a digits 1 et b digits -1. Il s’agit du nombre (3a+b+1-2×3b+1)/2.
Pour le minimum : min N(a, b) = (10...0-1...-1)_e avec a digits 0 et b - a digits -1. Il s’agit du nombre (2×3a+b-3b-a+1+1)/2.
Problème 2 : Compilation et algorithmes
A0 - Les graphes des modules
La partie A porte sur l’ordre dans lequel on compile différents modules : C’est un ordre topologique sur un graphe orienté. Un tel graphe peut être dessiné à l’aide du logiciel adéquat qui a servi à faire les figures ci-dessous.
Voici le graphe donné au début de la partie A de l’énoncé :
Dessiné, il ressemble à ceci :
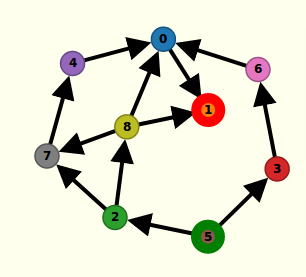
On constate qu’il ne possède qu’un sommet sans successeur (« arrivée ») et un seul sommet sans prédécesseur (« départ »). Cette dernière caractéristique permet de jouer à un jeu de Nim sur ce graphe, en plaçant un pion (noir ci-dessous) sur le sommet 5 (le départ) :
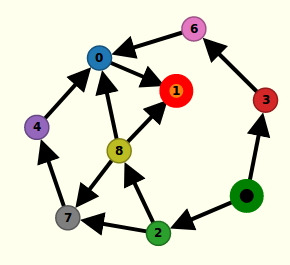
Les joueurs déplacent le pion selon une arête, chacun son tour. Celui qui mène le pion au sommet 1 (l’arrivée) gagne le jeu. On voit qu’il y a une stratégie gagnante pour celui qui joue en premier, consistant à mettre le pion sur le sommet 2. Ceci se voit par la coloration du graphe :
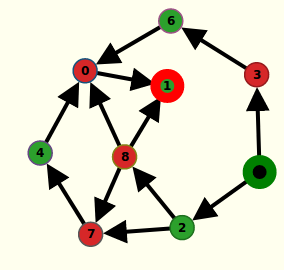
PARTIE A --- Ordre topologique sur un graphe
Le graphe de l’énoncé a été obtenu à partir du précédent en enlevant le sommet M2 :

Il est codé ainsi :
N = 9
App = [True, True, False, True, True, True, True, True, True]
P = 8
Succ = [[1], [], [], [6], [0], [3], [0], [4], [0, 1, 7]];
G = [App, Succ, P]Question 10
def mem(i, g):
"""renvoie True si le sommet numéro i est dans le graphe représenté par g"""
return g[0][i]Question 11
def pred(i, g):
"""renvoie la liste des sommets j tels que j->i est présent dans le graphe g."""
return [j for j in range(N) if mem(j, g) and i in g[1][j]]Par exemple :
>>> pred(0, G)
[4, 6, 8]Question 12
def sansSuccesseur(g):
"""renvoie un numéro i tel que Mi n'a pas de successeur
ou -1 si un tel sommet n'existe pas dans le graphe g"""
for i in range(N):
if mem(i, g) and g[1][i] == []:
return i
return -1Par exemple :
>>> sansSuccesseur(G)
1Question 13
import copy
def suppr(i, g):
"""crée et renvoie une copie de g privé du sommet i et des arcs qui s'y réfèrent"""
h = copy.deepcopy(g)
h[2] -= 1
h[0][i] = False
h[1][i] = []
for j in range(N):
if mem(j, h) and i in h[1][j]:
h[1][j].remove(i)
return hQuestion 14
On considère un graphe G de p sommets, p ≤ N.
(14a)
Promenade : s0s1...sN... on a donc N+1 sommets. Supposons que les sommets soient tous différents alors p = N+1 ce qui contredit l’hypothèse.
(14b)
Encore une fois par l’absurde : si on suppose que le graphe ne possède pas de cycle, alors à chaque pas de si vers sj on est sur un sommet non déjà visité. Mais alors cela signifie qu’à la fin de la promenade on a N+1 sommets distincts ce qui contredit (14a).
(14c)
D’après (14b), soit si0,si1...sik=si0 le cycle. Supposons qu’il existe un ordre topologique N. Alors par définition à la fois de l’ordre et de la promenade, on a : N(si0) < N(si1) < ... < N(sik) = N(si0) d’où N(si0) est strictement inférieur à lui-même ce qui n’est pas possible. Il n’existe donc pas d’ordre topologique sur ce graphe.
Question 15
Soit s1 et s2 deux sommets de G. Si s1 et s2 ne sont pas s alors si s1 est successeur de s2 on aura NH(s2) < NH(s1) et donc N(s2) < N(s1) et raisonnement analogue s’il s’agit de s2 successeur de s1. Donc N vérifie bien la condition d’ordre topologique.
Si maintenant s2 est le noeud s, alors comme s n’a pas de successeur, s2 ne peut pas être le successeur de s. s peut être le successeur de s2. Dès lors, N(s2) = NH(s2) ≤ p - 2 < p - 1 = N(s). Là encore la contrainte est vérifiée. N est donc bien un ordre topologique sur G.
Question 16
(16a) On en déduit un algorithme pour trouver un ordre topologique (quand il existe)
def ordreTopologique(g):
"""renvoie une liste L telle que L[i] vaut N(i)
si N existe et None sinon"""
n = len(g[0])
L = [-1] * n
def parcoursReussi(g):
p = g[2]
if p != 0:
s = sansSuccesseur(g)
if s == -1:
return False
else:
L[s] = p
return parcoursReussi(suppr(s, g))
else:
return True
b = parcoursReussi(g)
if b:
return L
else:
return None(16b) La seule fonction susceptible de boucler est parcoursReussi qui est récursive. Mais si p vaut 0 ou si on ne trouve pas de sommet sans successeur, ça termine. L’appel récursif se fait avec un graphe qui possède un de sommet de moins. On tombera donc sur un des deux cas :
- il n’y a plus de sommet : L’algorithme termine alors
- chaque sommet restant a au moins un successeur : Là encore l’algorithme termine.
Par exemple :
>>> print(ordreTopologique(G))
[7, 8, -1, 4, 6, 3, 5, 2, 1]B0 - Python et les registres
La partie B porte sur l’allocation de 4 registres aux variables a, b, c et d utilisées dans cette fonction Python :
def capes():
d = 1
b = 2*d
a = 3
d = a*b
print(d)
c = 2*a-b
print(a)
d = c+b
b = 2*a
print(c,d)Pour avoir les affichages du programme il suffit de lancer la fonction en entrant capes()
Mais pour savoir comment Python fait réellement l’allocation de registres, on pense naturellement à cet algorithme :
- Compiler la fonction capes() ci-dessus ;
- désassembler le bytecode ainsi obtenu ;
- regarder le résultat du désassemblage.
Pour cela on importe le module dis (comme « disassemble ») qui possède une fonction dis s’appliquant à toute fonction Python, comme par exemple la fonction capes() ci-dessus. En précédant la définition de la fonction d’un from dis import * et en la suivant d’un dis(capes) on obtient ceci :
4 0 LOAD_CONST 1 (1)
3 STORE_FAST 0 (d)
5 6 LOAD_CONST 2 (2)
9 LOAD_FAST 0 (d)
12 BINARY_MULTIPLY
13 STORE_FAST 1 (b)
6 16 LOAD_CONST 3 (3)
19 STORE_FAST 2 (a)
7 22 LOAD_FAST 2 (a)
25 LOAD_FAST 1 (b)
28 BINARY_MULTIPLY
29 STORE_FAST 0 (d)
8 32 LOAD_GLOBAL 0 (print)
35 LOAD_FAST 0 (d)
38 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
41 POP_TOP
9 42 LOAD_CONST 2 (2)
45 LOAD_FAST 2 (a)
48 BINARY_MULTIPLY
49 LOAD_FAST 1 (b)
52 BINARY_SUBTRACT
53 STORE_FAST 3 (c)
10 56 LOAD_GLOBAL 0 (print)
59 LOAD_FAST 2 (a)
62 CALL_FUNCTION 1 (1 positional, 0 keyword pair)
65 POP_TOP
11 66 LOAD_FAST 3 (c)
69 LOAD_FAST 1 (b)
72 BINARY_ADD
73 STORE_FAST 0 (d)
12 76 LOAD_CONST 2 (2)
79 LOAD_FAST 2 (a)
82 BINARY_MULTIPLY
83 STORE_FAST 1 (b)
13 86 LOAD_GLOBAL 0 (print)
89 LOAD_FAST 3 (c)
92 LOAD_FAST 0 (d)
95 CALL_FUNCTION 2 (2 positional, 0 keyword pair)
98 POP_TOP
99 LOAD_CONST 0 (None)
102 RETURN_VALUECe qui permet de suivre la chronologie de l’exécution du programme :
- t=0 : La constante 1 est chargée par la machine Python
- t=3 : La constante est stockée dans la variable d (la ligne 1 du programme est effectuée)
- t=6 : La constante 2 est chargée
- t=9 : Le contenu de d est chargé
- t=12 : La multiplication 2*d est effectuée
- t=13 : Le résultat est stocké dans b (la ligne 2 est alors effectuée)
- t=16 à 21 : 3 est mis dans a (ligne 3 du programme Python)
- t=22 à 31 : a*b est mis dans d
- t=32 : C’est une fonction (globale) et non une constante qui est chargée : print
- t=35 : d est chargé aussi
- t=36 : La fonction print est appelée avec l’argument (contenu de) d
- t=39 : puis dépilée (ce qui se passe à chaque return ; en effet la machine Python est basée sur une pile)
- t=42 à 55 : 2*a-b est mis dans c (on constate que la suite des opérations est menée sur la pile avec la notation polonaise inversée 2 a * b - dans l’ordre d’exécution)
- t=56 à 65 : L’affichage de a est effectué
- t=66 à 75 : c+b est mis dans d
- t=76 à 85 : 2*a est mis dans b
- t=86 : La fonction print est empilée
- t=89 : La variable c est chargée
- t=92 : La variable d est chargée
- t=95 : La fonction print est appelée (mais cette fois-ci avec deux arguments)
- t=98 : La fonction est dépilée
- t=99 : La constante 0 (signifiant qu’il n’y a pas eu d’erreur) est chargée
- t=102 : La constante 0 est renvoyée par la fonction capes()
Comme on le voit, les registres du processeur et la manière dont les variables a, b, c et d leur sont allouées, ne sont pas affichés. C’est parce que la machine virtuelle Python n’est basée que sur cette pile. Ce sont les longueurs successives de la pile qui sont affichées dans l’avant-dernière colonne.
On note que c’est la deuxième année de suite que le sujet de Capes porte sur la notion de graphe d’intervalles.
PARTIE B --- Allocation de registres
Question 17
| ligne | a | b | c | d |
| 0 | M | M | M | M |
| 1 | M | M | M | V |
| 2 | M | V | M | M |
| 3 | V | V | M | M |
| 4 | V | V | M | V |
| 5 | V | V | M | M |
| 6 | V | V | V | M |
| 7 | V | V | V | M |
| 8 | V | M | V | V |
| 9 | M | M | V | V |
Question 18
Si par exemple la variable a est vivante en ligne 0, cela signifie qu’elle est utilisée sans avoir été initialisée. Dans ce cas le programme ne s’exécute pas, il s’interrompt avec ce message :
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'a' is not definedIl ne serait donc pas exécutable.
Question 19
""" PROG_EX:"""
d=1
b=2∗d
a=3
d=a∗b
print(d)
c=2∗a−b
print(a)
d=c+b
b=2∗a
print(c,d)
PROG_EX = [(3,[]), (1,[3]), (0,[]), (3,[0,1]), (None ,[3]), (2,[0,1]), (None ,[0]), (3,[1,2]), (1,[0]), (None ,[2,3])]def determineVie(prog, p):
"""retourne le tableau de vie d'un programme prog de p variables"""
nb_instructions = len(prog)
vie = [[False] * p for _ in range(nb_instructions+1)]
for index in range(nb_instructions - 1, -1, -1):
left, variables = prog[index]
for v in range(p):
if v in variables:
vie[index][v] = True
else:
vie[index][v] = vie[index+1][v]
if left is not None:
vie[index][left] = left in variables
return vie[:-1]Pas de difficulté particulière sur ce code : on parcourt les lignes de la table en remontant et en mettant à jour la vie d’une variable comme expliqué. Petite astuce la liste de vie comporte une ligne de plus pour ne pas avoir à traiter comme cas particulier la dernière ligne, d’où le vie[:-1] à la fin.
Par exemple :
>>> VIE_EX = determineVie(PROG_EX, 4)
>>> for line in VIE_EX:
print(line)
[False, False, False, False]
[False, False, False, True]
[False, True, False, False]
[True, True, False, False]
[True, True, False, True]
[True, True, False, False]
[True, True, True, False]
[True, True, True, False]
[True, False, True, True]
[False, False, True, True]Question 20
def periodesVie(vie, v):
n = len(vie)
periodes = []
enCours = False
i = n - 1
while i >= 0:
if vie[i][v]:
if not enCours:
periode = (i,)
enCours = True
else:
if enCours:
periode = (i,) + periode
enCours = False
periodes.append(periode)
i -= 1
return periodesPar exemple :
>>> periodesVie(VIE_EX, 3)
[(7, 9), (3, 4), (0, 1)]PARTIE C --- Graphe de coexistence
Dans cette partie, c’est le logiciel des graphes non orientés qui sera utilisé. Il a servi notamment à dessiner les graphes ci-dessous.
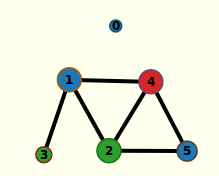
On a vu dans la question 17 que toute variable parmi a, b, c et d est utilisée en même temps que toute autre variable parmi elles. Si on représente par un graphe la relation « est utilisée en même temps que », le graphe correspondant, pour ces 4 variables, est le graphe K_4 complet à 4 sommets (0 pour a, 1 pour b etc) :

Si on représente chaque registre par une couleur, il faut donc 4 couleurs pour colorier ce graphe. Ce qui signifie qu’au moins 4 registres seront nécessaires pour faire tourner ce programme. La partie C porte sur un autre graphe, que voici au format Nirina974 :
Le graphe ressemble à ceci :
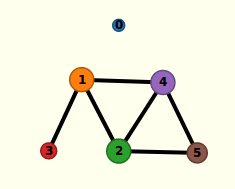
On remarque que ce graphe est dessiné comme un réseau social, avec des sommets dont le diamètre est fonction croissante du degré.
Question 21
- Un problème de décision (de la forme existe-t-il... ?) est dit dans la classe NP s’il existe un algorithme en temps polynomial pour vérifier qu’une solution donnée en est une.
- Un problème est NP-complet si tout problème de la classe NP se ramène à celui-là par une réduction polynomiale (en pratique il suffit d’en trouver un).
Dans la suite on se donne :
COLORS = ['bleu', 'rouge', 'vert']
G_EX = [[], [2, 3, 4], [1, 4, 5], [1], [1, 2, 5], [2, 4]]
COLOR_EX = [0, 0, 1, 1, 2, 0] Question 22
def bonnesCouleurs(g, couleurs):
"""retourne True si et seulement si couleurs est une coloration correcte
des sommets de g ie que tous les sommets de g sont bien coloriés."""
def sommet_bien_colorie(s):
# un sommet s est bien colorié s'il n'a pas la même couleur que ses voisins
# autrement dit : si tous ses voisins ont une couleur différente
return all(couleurs[s] != couleurs[v] for v in g[s])
return all(sommet_bien_colorie(s) for s in range(len(g)))La fonction python all (présentée dans cet article) permet une solution particulièrement concise et élégante de la fonction bonnesCouleurs : un graphe est bien colorié si tous ses sommets sont bien coloriés. Un sommet est lui même bien colorié s’il ne partage pas sa couleur avec l’un de ses voisins.
Par exemple :
>>> bonnesCouleurs(G_EX, COLOR_EX)
TrueQuestion 23
L’énoncé donnait cet algorithme pour trouver une bonne coloration (aucune garantie sur la minimalité de cette coloration) :
- choisir la première couleur disponible ;
- tant qu’il existe un sommet non colorié répéter les étapes 3 à 6 :
- choisir un sommet s non colorié, et le colorier avec la couleur courante ;
- répéter l’étape 5 pour tout sommet t non colorié ;
- si t n’est adjacent à aucun sommet colorié avec la couleur courante, le colorier avec la couleur courante ;
- choisir une nouvelle couleur ;
- fin de l’algorithme.
Voici la traduction de l’algorithme sous forme de fonction Python :
def coloriage(g):
nb_sommets = len(g)
une_couleur = 0
couleurs = [None] * nb_sommets
s_non_colories = list(range(nb_sommets))
while s_non_colories:
s = s_non_colories.pop()
couleurs[s] = une_couleur
for t in s_non_colories[:]:
if coloriable(g[t], couleurs, une_couleur):
couleurs[t] = une_couleur
s_non_colories.remove(t)
une_couleur += 1
return couleurs
def coloriable(voisins, couleurs, c):
return all(couleurs[v] != c for v in voisins)Par exemple :
>>> coloriage(G_EX)
[0, 0, 2, 1, 1, 0]C’est bien le coloriage de l’énoncé :



Commentaires