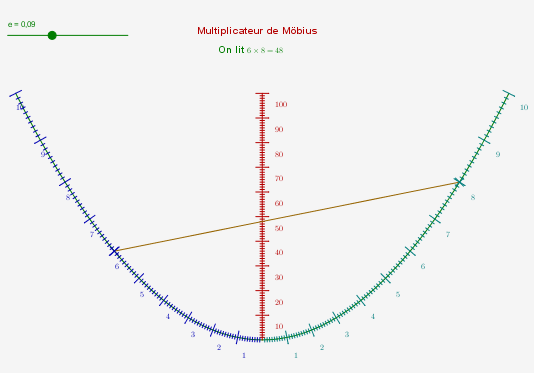
Pour construire graphiquement le produit de deux nombres positifs (ici ce sont des entiers) $a$ et $b$, on peut s’aider de la parabole d’équation $y=(a+b)x-x^2$ qui coupe l’axe des abscisses aux points d’abscisses 0 et $a+b$, et passe par les points de coordonnées $(1 ;a+b-1)$ et $(a+b-1,a+b-1)$ (ce dernier point peut se construire comme intersection de la parabole et de la bissectrice $y=x$) et dont le sommet a pour coordonnées $\left(\frac{a+b}{2} ;\frac{(a+b)^2}{4} \right)$. L’équation de la parabole permet de montrer que celle-ci passe aussi par les points de coordonnées $(a ;ab)$ et $(b ;ab)$ (facile en mettant $x$ en facteur) : Il suffit alors de lire l’ordonnée commune des deux points d’abscisses respectives $a$ et $b$ sur la parabole [1] :
N’ayant pas eu la chance de disposer de CaRMetal en 1841, August Ferdinand Möbius a dessiné un faisceau de paraboles dans son article, lisible (pour ceux qui comprennent l’allemand) sur Gallica, et dont la figure 1 est reproduite ici :
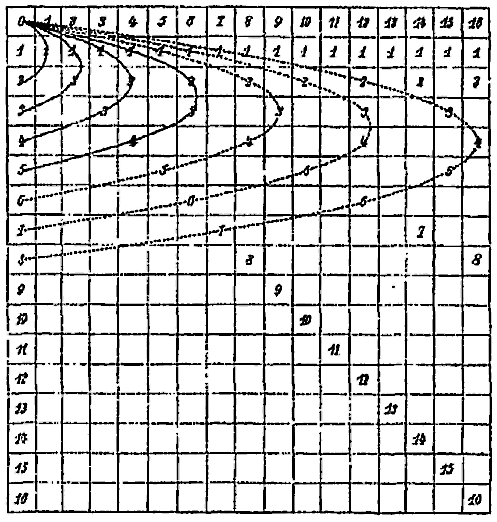
Ce qu’on voit sur la figure de Möbius, et pas sur le fichier CaRMetal ci-dessus, c’est l’idée selon laquelle pour Möbius, une parabole est une droite projective, donc munie de graduations, idée qui est à la base du nomogramme suivant :
Il se trouve que la parabole $y=x^2$ est au programme de Seconde, ainsi que ses intersections avec des droites, ça tombe bien...
La seule difficulté en Asymptote est le calcul de vecteurs normaux
pour représenter les graduations.
Le programme ci-dessous donne le fichier pdf téléchargeable en bas de l’article :
Si le texte et les graduations sont si minuscules, c’est pour agrandir en A3 (après avoir imprimé le pdf téléchargeable ci-dessous).
On peut multiplier deux nombres inférieurs à 10 en tendant un fil sur une parabole !
Applications
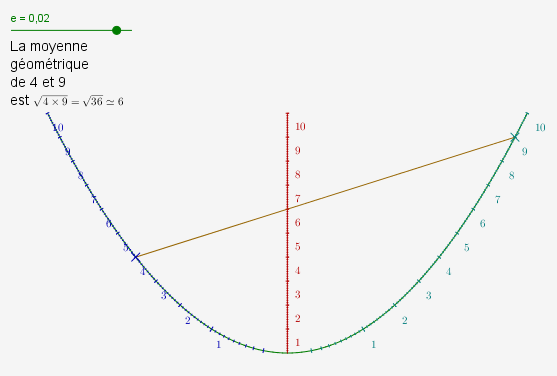
Si, au lieu de mettre des graduations dont les abscisses sont régulières, on met sur la même parabole, des graduations dont les ordonnées sont régulières, on obtient un nomogramme qui calcule la moyenne géométrique de deux nombres positifs :
Une autre application du multiplicateur de Möbius est visible dans l’article sur l’IMC.


Commentaires