>VIDEO sur l’histoire de la trigonométrie

REMERCIEMENTS :

UN GRAND REMERCIEMENT AUX WEBMASTERS DES SITES SUIVANTS POUR LEURS INFORMATIONS ET LEURS IMAGES « LIBRES » sans brevet :

– Merci aux enseignants de l’académie de Clermont-Ferrand pour leur excellente banque de données mise à la disposition des enseignants, tout particulièrement pour l’article sur la trigonométrie de Jean Philippe Darras.
– Merci à Daniel Joly pour son bel article sur les ondes radio et pour l’autorisation de publier une image de son site.
– Un grand merci à Wikimedia Commons pour toutes ces images libres qui m’ont permis de réaliser le diaporama sur l’histoire de la trigonométrie.
– Merci à Wikipédia pour l’histoire des mathématiciens arabes.
– Merci au webmaster de Chronomath pour son excellent site.

1. Activité de découverte

2. Visualisation en géométrie dynamique

Cette figure permet de faire apparaître la courbe sinusoïdale à partir d’un cercle :

<geogebra|doc=3304|largeur=800|hauteur=650>

3. Un peu d’histoire

-------------> VIDEO HISTOIRE DE LA TRIGONOMETRIE Il y a 4 000 ans, les astronomes babyloniens cherchaient à mesurer la distance aux astres, et ne pouvaient que mesurer des angles. C’est ainsi qu’ils décidèrent de créer les premières tables astronomiques en partageant le cercle en 360°, car ils comptaient en base 60. La mesure d’angle que l’on connait à ce jour était née.	Tables babyloniennes

Au III^e siècle avant J.-C., en Inde, le sinus de 45° fut calculé avec une procédure pour cercler un carré mais les Indiens n’étendirent pas la notion pour d’autres angles.

C’est en Grèce, à la même époque, que la trigonométrie allait vraiment commencer.

Ératosthène de Cyrène (-276 ; -196) et Aristarque de Samos (-310 ; -230) utilisent les tables astronomiques des babyloniens. Ératosthène se rendra célèbre pour avoir calculé la circonférence de la terre avec une précision tout à fait remarquable (seulement 3% d’erreur).

Ératosthène de Cyrène	Aristarque de Samos

Mais c’est un siècle plus tard qu’un Grec nommé Hipparque de Nicée (-190 ; -120 ), à la suite d’un immense travail d’observation des étoiles, créa les premières tables de cordes, permettant dans un cercle de trouver la longueur d’une corde en fonction de l’angle au centre qui lui est associé.

Cela lui permis de découvrir que l’axe de la terre n’est pas fixe.

Hipparque conçoit un instrument de mesure et de calcul, l’astrolabe, permettant d’établir la hauteur d’un astre par rapport à l’horizon. À partir du IX^e siècle, cet instrument se diffusera grandement dans le monde arabe.

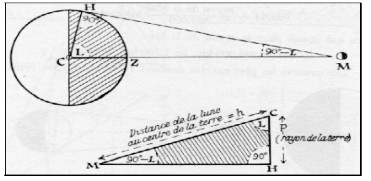
On doit à Hipparque l’usage des parallèles et des méridiens pour se repérer sur la terre. À l’aide de ses tables, il a pu calculer la distance de la terre à la lune, et a trouvé 400 000 km, soit à peine 2% d’erreur ! Grâce à ce calcul, il a aussi trouvé le rayon puis la circonférence de la lune. La trigonométrie était née.

Hipparque de Nicée	Corde dans un cercle	Astrolabe	Calculs astronomiques

Un siècle plus tard, le Grec Claude Ptolémée (90 ? ; 160 ?) poursuit dans l’Almageste les travaux d’Hipparque avec une meilleure précision et introduit les premières formules de trigonométrie. Ces tables sont les premiers exemples de fonction dans l’histoire des mathématiques. C’est à cette époque que les Grecs prennent l’habitude de diviser le cercle en 360°.

Claude Ptolémée	Table des cordes

La deuxième partie de l’histoire de la trigonométrie va se passer en Inde.

En effet, il faudra attendre le cinquième siècle après J.-C. pour qu’en Orient, un mathématicien indien du nom de Aryabhata l’Ancien (476 ; 550) eut la bonne idée d’utiliser la demi corde (au lieu de la corde).

Aryabhata	demi corde dans un cercle	Tables d’Aryabhata

Les Indiens ont ainsi remplacé la table des cordes par les premières tables de demi cordes, ou table des sinus. On retrouve la configuration du sinus dans le triangle rectangle telle qu’elle est enseignée aux collégiens aujourd’hui. Aryabhata est le premier à voir la trigonométrie hors du cercle. Le mot sanscrit « jiva » désignant la demi corde devint « jiba » en arabe, puis sinus en latin, qui signifie « demi corde ». Il définit ainsi le sinus puis le cosinus comme « contre sinus ».

Un autre mathématicien indien, Varahamihira, établit la formule $sin^2x + cos^2x = 1 $. La grande originalité des Indiens est d’avoir inventé la numération positionnelle que nous utilisons encore aujourd’hui. 800 se lit “huit cents” car le chiffre 8 est placé à une certaine position. Cette numération va révolutionner les mathématiques.

La troisième partie de la trigonométrie va se dérouler dans le monde arabe.

La Perse était alors d’une grande richesse intellectuelle. La recherche astronomique étant vivement encouragée par le calife Abbaside Al Ma’mun, Bagdad et Damas étaient alors les nouveaux centres de la science.

Dès le VIII^e siècle, les mathématiciens arabes traduisirent les ouvrages provenant d’Inde. C’est à Bagdad que Mohammad Khwarizmi (750-850) établit les premières tables des sinus. C’est à partir de son nom, Khwarizmi qu’est né le mot “algorithme”, si utilisé en informatique de nos jours, tandis que le mot “algèbre” provient du titre d’un de ses livres.

Juste après, Al-Hasib, appellé le calculateur, originaire d’Égypte, (fin IX^e s., début X^e s.) inventa la tangente, qui est l’objet idéal pour mesurer les hauteurs. Le mot tangente vient du latin « tangere » qui veut dire toucher.

Mohammad Khwarizmi	Al-Hasib

Au IX^e siècle Mohammed Al Battani (850 ; 929) introduit les tables des tangentes d’un angle et de nouvelles formules comme $ tan(x)=sin(x)/cos(x) $.

Quand au choix du rayon 1, il fut initié par un mathématicien d’origine iranienne qui se fit connaître à Bagdad, Abu Al-Wafa (950 – 998). Il développe notamment les nombres négatifs pour permettre aux banquiers de calculer les dettes à l’aide des nombres.

Mohammed al Battani	Abu al-Wafa

Au XIII^e siècle, avec le Perse Al Tusy (1201-1274), la trigonométrie se sépare alors définitivement de l’astronomie.

Enfin, au XIV^e siècle, Al-Kashi réalise, durant ses études, des tables de fonctions trigonométriques. Il découvre également une relation qui permet de calculer la longueur des côtés dans un triangle quelconque, Cette relation sera appellée le théorème d’Al Kashi , appellé également théorème de Pythagore généralisé ou loi des cosinus.

Al Tusy	Al-Kashi

La dernière partie de l’histoire de la trigonométrie se déroulera en Occident.

À partir du XII^e siècle, de nombreux ouvrages scientifiques sont traduits en latin. La Renaissance sortira l’Europe de son sommeil.

Au XV^e siècle, l’astronome et mathématicien allemand Regiomontanus, de son vrai nom Johann Müller développe la trigonométrie comme une branche indépendante des mathématiques. Il serait à l’origine de l’usage systématique du terme sinus.

Au XVI^e siècle, le Français François Viète, conseiller d’Henri IV, fera évoluer la trigonométrie pour lui donner le caractère qu’on lui connaît aujourd’hui. Albert Girard (1595, 1632) introduisit les notations sin, cos et tan.

Johann Müller	François Viète	Albert Girard

Au XVII^e siècle, René Descartes (1596-1650) montre que l’on peut utiliser les sinus pour calculer la déviation d’un rayon lumineux, appellée réfraction de la lumière. À partir de là, on utilise la trigonométrie dans toutes les branches de la physique.

Au XVIII^e siècle, le physicien allemand Ernst Chladni, en étudiant la propagation du son dans un solide, donna une image de vibrations sonores sous forme d’ondes.

Au XIX^e siècle, le baron français Joseph Fourier a fourni l’outil mathématique pour étudier les phénomènes vibratoires, appelé « les séries de Fourier ». Ces séries se retrouvent dans beaucoup de domaines comme l’étude du courant électrique, des ondes cérébrales, du traitement de l’image.

René Descartes	Ernst Chladni	Joseph Fourier

La trigonométrie a donc permis de découvrir le vaste domaine des ondes.

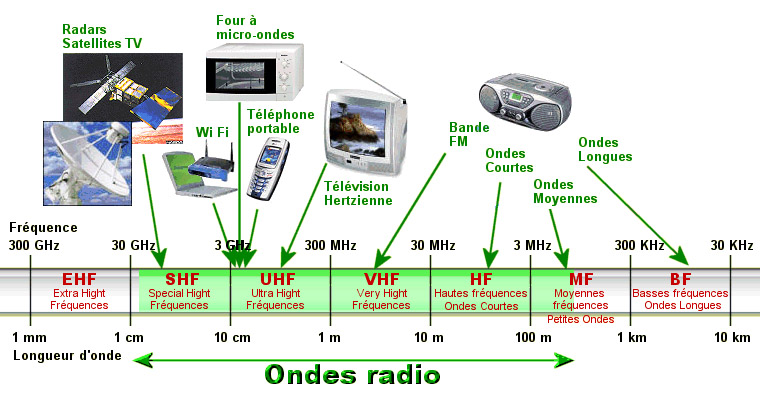
L’étude de ces ondes a permis d’inventer toutes sortes d’instruments permettant de transmettre le son puis l’image, comme le sonographe, la radio, puis la télévision le téléphone, l’ordinateur, avec des modes de transmissions de plus en plus élaborés comme la wifi, le GPS et la transmission satellite.

L’étude de ces ondes a également permis d’inventer toutes sortes d’instruments permettant de voir à l’intérieur de nos corps, comme la radiographie puis le scanner et l’irm, permettant le formidable progrès actuel de la médecine.

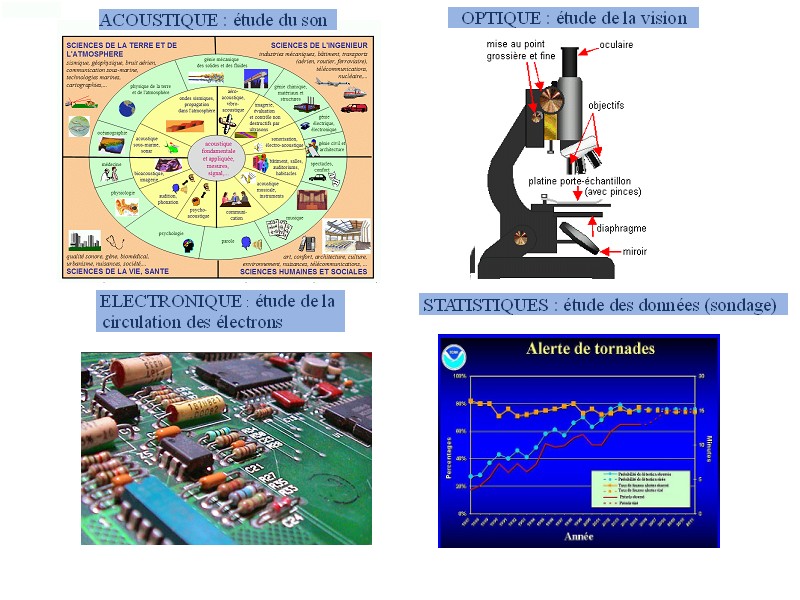
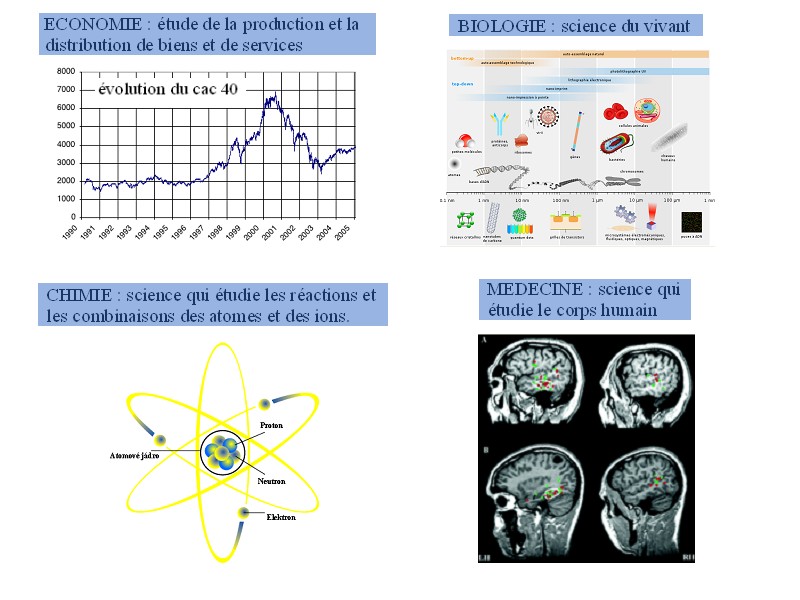
Aujourd’hui, la trigonométrie trouve des applications très diverses, dans une multitude de sciences : acoustique, optique, électronique, statistiques, économie, biologie, chimie, médecine, physique, météorologie, géodésie, géographie, cartographie, cryptographie.

Que de chemin parcouru grâce à la trigonométrie...

4. Applications autour de la trigonométrie

Première application de la trigonométrie : La navigation en mer

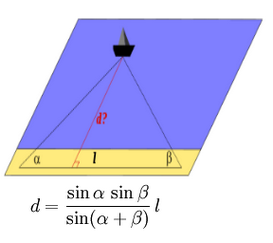
La première application de la trigonométrie est le principe de triangulation, permettant en fonction de deux endroits de déterminer un troisième endroit. Une des premières applications de la trigonométrie est donc la navigation (l’orientation en mer).

a) La trigonométrie permit de calculer la distance d’un bateau à une côte

Pour avoir une mesure approximative de cette distance, Thalès de Milet plaça deux observateurs A et C sur le rivage, éloignés d’une distance b connue.

Il demanda à chacun d’entre eux de mesurer l’angle que font les droites passant par le bateau B et l’un d’entre eux, et la droite passant par les deux observateurs.

Cette méthode a un intérêt si nous voulons déterminer de grandes distances. Mais dans ce cas nous devons placer les deux observateurs suffisamment éloignés l’un de l’autre, pour que les mesures d’angle soient plus précises.

b) Navigation par un amer : comment se repérer en mer lorsqu’on aperçoit une terre

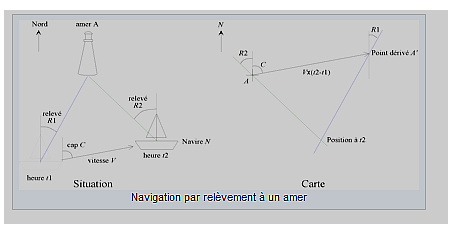
Jusque dans les années 1980, on utilisait essentiellement la triangulation pour mesurer les distances.

Le navire est placé à un point B, et voit la lumière d’un phare (point A). On mesure l’angle fait entre la droite (AB) et le Nord indiqué par une boussole. On obtient la mesure de l’angle R1.

Le bateau dérive à une certaine vitesse, il se trouve alors en un point C. On mesure l’angle fait entre la droite (AC) et le Nord, on obtient la mesure de l’angle R2.

On se trouve donc dans un triangle ABC dont on connait les angles et la mesure d’un côté (BC). On applique alors le procédé de triangulation, ce qui permet de se repérer en mer.

Deuxième application de la Trigonométrie : La mesure de grands espaces

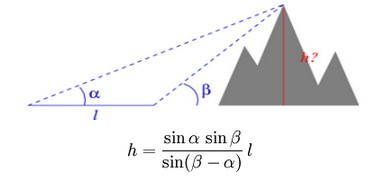
a) Calcul de la hauteur d’une montagne (calculs qui développèrent l’architecture, permettant la construction de grands édifices comme les cathédrales) :

b) Le calcul de longues distances (cartographie)

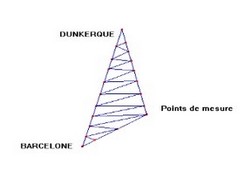
Ce procédé de triangulation, répété de proche en proche, a été utilisé par Delambre et Méchain de 1792 à 1798 pour mesurer la distance entre Dunkerque et Barcelone (environ 1 147 km) sur le méridien de Paris.

Ce qui permettra la première définition du mètre en 1799.

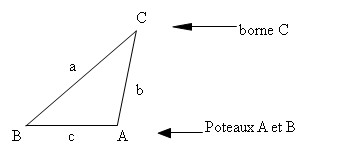
c) L’arpentage d’un terrain

On découpe le terrain en différents triangles (voir figure A) et on mesure leurs aires.

découpage d’un terrain : figure A	Mesures de l’aire du triangle : figure B

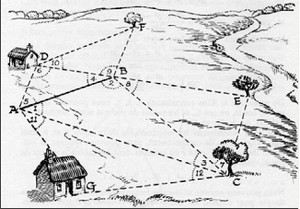
Pour mesurer l’aire d’un triangle , on va procéder ainsi :

La démarche habituelle (voir figure B) consiste à planter deux poteaux aux points A et B, et avec un décamètre ou une chaîne d’arpenteur et à mesurer la distance c qui les sépare (« la ligne de base »). Remplacez ensuite le poteau A par une lunette d’arpenteur munie d’un plateau divisé en 360 degrés permettant de repérer sa direction (« azimut »).

En visant successivement une borne C puis le poteau B, vous obtenez l’angle A du triangle ABC par soustraction des valeurs lues sur le plateau d’azimut.
À partir du point B on mesure l’angle B de façon analogue.

Troisième application de la trigonométrie : L’étude des ondes

La ressemblance entre la forme d’une corde vibrante et une sinusoïde n’est pas un hasard...

a) La transmission du son dans un téléphone

1^er cas : transmission analogique d’une voix (le téléphone des années 1980)

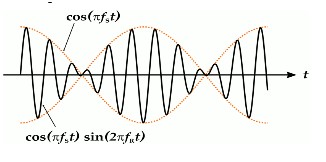
Une voix émet une onde d’une fréquence de 4 MégaHertz (Mhz) : Figure A ci- dessous

Le câble du téléphone peut transmettre des ondes d’une autre fréquence (entre 48 et 106 Mhz) : figure B

L’astuce pour faire passer l’onde de la voix dans le câble consiste à créer une troisième onde qui a la fréquence d’onde du câble mais garde les caractéristiques de l’onde de la voix : Figure C. Ce procédé s’appelle la modularisation du signal. On obtient donc l’onde suivante qui peut ainsi passer dans le câble.

À la sortie du câble, on refait le procédé inverse et on obtient une onde qui,
au travers d’un aimant et d’une paroi qui vibre, va retransmettre le son de la voix du départ.

longueur d’onde de la voix	Longueur d’onde du câble	Longueur d’onde modularisée
Figure A	Figure B	Figure C

2^e cas : transmission numérique d’une voix (le téléphone portable de nos jours)

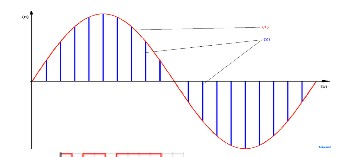
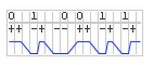
L’onde de la voix est échantillonnée (approximée par un diagramme en bâton) : figure D ci-dessous. En rouge, on voit l’onde de la voix, et en bleu, l’onde digitalisée (diagramme en bâtons).

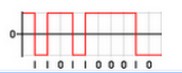
Chaque rectangle est codé en binaire (exemple : 0011 1101), on obtient un signal numérique : figure E .

Ce signal numérique est transmis via un câblage spécifique permettant la transmission du codage binaire.
À l’arrivée, à partir du codage binaire, on reconstitue l’onde de la voix (figure F)
et au travers d’un aimant et d’une paroi qui vibre on recrée ainsi la voix du départ.

Onde de la voix échantillonnée	Codage de l’onde en binaire	Conversions Binaire analogique
Figure D	Figure E	Figure F

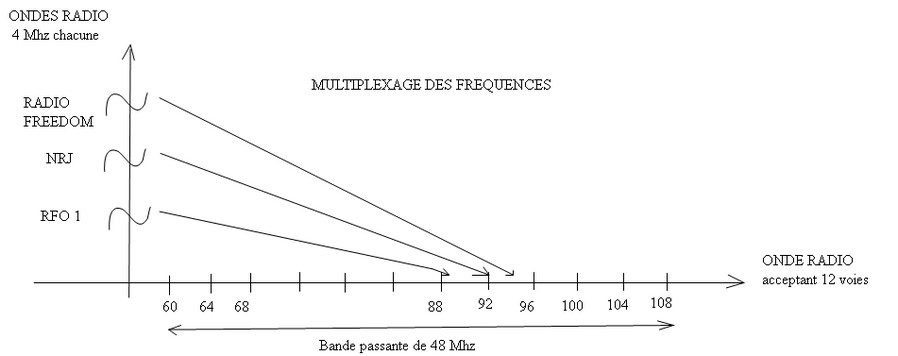
b) L’étude des ondes : la radio FM

Chaque radio émet un son d’une longueur d’onde de 4 Mhz. On attribue à chaque radio une longueur d’onde sur la bande passante .

Par exemple, NRJ correspond à la longueur d’onde 92,8 Mhz. On transforme donc l’onde de la voix de la radio NRJ en une autre onde de fréquence plus élevée.

On fait de même avec les autres radios. Cette opération s’appelle le multiplexage de fréquence. On fait le procédé inverse pour retrouver la voix des radios.

Quand dans une bande passante, on choisit une fréquence, on entend une voix correspondant à la radio que l’on souhaite entendre.

On parle de bande FM car en changeant de radio, on change de fréquence, on parle alors de Modulation de Fréquence (FM).

c) Le scanner

On envoie un rayon X à travers le corps d’un patient. Ce rayon traverse le corps et se réfléchit sur une plaque de cristal qui se met à vibrer créant une onde dont on mesure l’intensité. Le rayon X sera freiné en passant dans les différentes parties du corps.

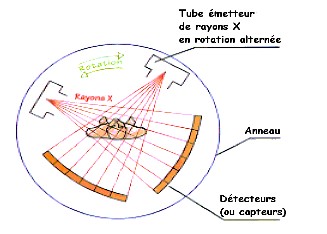
À chaque endroit du corps scanné correspond donc une longueur d’onde précise. À l’aide de ces données, on reconstitue l’image en faisant correspondre une couleur (ou un dégradé de gris) à chaque longueur d’onde. On obtient une image de l’intérieur du corps du patient.

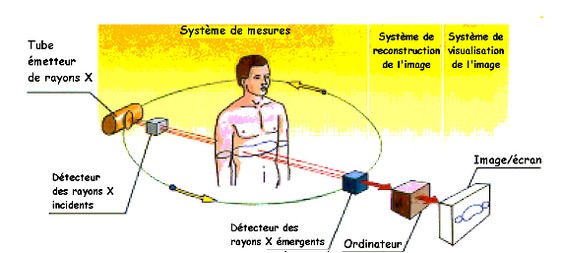
On mesure l’intensité de ce rayon avant et après le passage du rayon X dans le corps du patient à l’aide de détecteurs de rayon X.

Par exemple, la tumeur cancéreuse est très dense et ralentit énormément le rayon X. Il va donc se réfléchir sur le cristal avec beaucoup moins d’intensité. En fait, lorsqu’on voit l’image d’un cancer par scanner, ce n’est pas la tumeur que l’on voit mais l’image des rayons qui ont traversé cette tumeur.

Le détecteur des rayons X émergents mesure l’intensité du rayon X après le passage du rayon dans le corps.
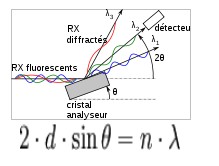
Il est constituée d’un monocristal qui décompose les ondes produites par le rayon X lorsqu’il tourne et mesure leurs intensités.

L’énergie des photons diffractés est donnée par la loi de Bragg :
où λ est la longueur d’onde de la radiation,
d est la distance du plan cristallin diffractant,
et n est un nombre entier appelé « ordre de diffraction »,

d) L’utilisation des ondes en ce début du XXI^e siècle :

Des domaines scientifiques liés à la trigonométrie

Beaucoup de sciences utilisent la trigonométrie de nos jours !

5. Cours de classe de 3^e sur la trigonométrie

Télécharger le cours :