Graphes non orientés
Les graphes non orientés ci-dessous ont été utilisés depuis la semaine des maths 2018 pour jouer à divers jeux :
Quoi faire avec ?
Pour chacun de ces graphes non orientés, on peut
- placer des pions (prédateurs, gendarmes ou chiens) pour un des joueurs et un pion (proie, voleur ou tangue) pour l’autre joueur, et le premier essaye de bloquer l’autre en bougeant un seul de ses pions à la fois. Ces jeux sont très anciens ;
- analyser le jeu ci-dessus en cherchant où placer les chiens et le tangue pour équilibrer le jeu ;
- jouer au jeu de Col : Chaque joueur à son tour colorie un sommet encore blanc du graphe, en évitant de colorier de la même couleur deux sommets adjacents du graphe ;
- jouer au jeu de Snort : Comme ci-dessus mais cette fois-ci il ne faut pas colorier deux sommets adjacents dans des couleurs différentes ;
- colorier les sommets du graphe sans jamais que deux sommets adjacents soient de même couleur, et en minimisant le nombre total de couleurs utilisées (son nombre chromatique) ;
- inscrire dans chaque sommet le degré de celui-ci (optionnellement, reproduire les sommets et leurs degrés sans donner les arêtes, puis demander à un autre joueur de reconstituer le graphe) ;
- inscrire dans chaque sommet la distance au sommet du graphe qui est le plus éloigné de celui-ci [1] ;
- parcourir le graphe, sommet après sommet, avec un seul pion, sans jamais passer par un sommet déjà visité ;
- jouer à des jeux de semaille, les graines étant semées en suivant un chemin du graphe (chaque graine doit être semée dans un sommet adjacent à la graine précédente) ;
- jouer (à un seul joueur) à sliding tokens, une généralisation de rush hour (casse-tête) à un graphe quelconque, où on place des pions sur des sommets non adjacents et chaque mouvement consiste à déplacer un pion vers un sommet adjacent à sa position actuelle mais adjacent à aucun autre sommet occupé. Le but du jeu est de mener un pion (rouge) à un sommet d’arrivée, quitte à bouger tous les autres pions (bleus) pour lui libérer le passage [2].
Une histoire vraie
L’histoire se joue entre trois personnages, que nous allons nommer, respectivement, la grande sœur, le petit frère et le tonton. Le tonton est animateur IREM et il lui arrive parfois d’occuper les enfants à des jeux sur les graphes orientés (voir plus bas). La grande sœur fait partie des plus acharnés parmi les joueurs de Nim et dès l’âge de 7 ans elle a régulièrement créé ses propres graphes orientés. L’un de ces graphes (dessiné un peu avant le huitième anniversaire de la grande sœur) comporte 6 sommets :
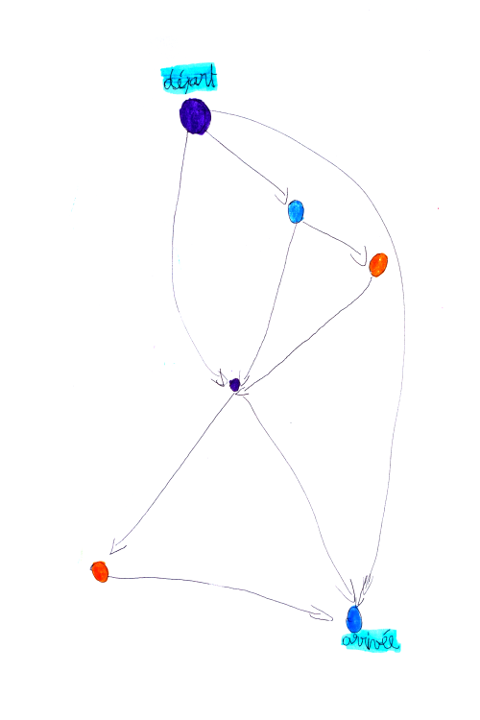
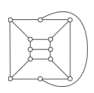
Le tonton n’a toutefois pas été satisfait par ce graphe, en effet il y a une arête allant directement du départ à l’arrivée, ce qui, selon le tonton, « diminue considérablement l’intérêt du jeu ». Et oui, ils sont parfois exigeants, les tontons ! Ceci dit, le tonton a alors imaginé deux variantes du graphe, l’une obtenue en enlevant l’arête en question, l’autre en enlevant l’orientation du graphe. Voici les résultats obtenus :
| version orientée | version non orientée |
Par la suite, à l’occasion d’un jour de pluie, les trois personnages, privés d’école, ont passé plusieurs heures à tester les graphes non orientés ci-dessus, en cherchant notamment comment colorier ces graphes, (et une fois le petit frère lassé) comment gagner au jeu de Col sur ces mêmes graphes. Mais surtout la grande sœur et le tonton se sont longuement posés, graphe après graphe, la question du nombre minimum de chiens à placer sur les graphes pour que ceux-ci aient une chance de bloquer le tangue (voir ci-dessous pour des précisions sur ce vocabulaire). La question s’est évidemment posée aussi sur le graphe non orienté de cette histoire : Comme il y a un sommet de degré 2, il y a des chances que 2 chiens suffisent pour bloquer le tangue. Ni la grande sœur ni le tonton n’ont alors eu le temps de chercher si dans ce cas les deux chiens bénéficient d’une stratégie gagnante.
L’épisode suivant de cette histoire est la semaine des maths où le graphe a eu un grand succès, notamment auprès des plus jeunes, probablement parce qu’il n’a que 6 sommets. Ce sont surtout les activités de coloriage qui y ont été menées. Et pendant ce temps, le petit frère n’a cessé de manifester son envie de jouer sur les graphes comme sa grande sœur. C’est peu après son quatrième anniversaire que le tonton a accédé à sa requête en lui présentant les graphes non orientés, l’un après l’autre, pour lui demander sur lequel il préférait jouer. Étant depuis peu élève en moyenne section, il a choisi le graphe qui est à la fois le plus simple et le plus gros, à savoir celui de notre histoire.
Il a choisi que l’un des joueurs dispose du pion orange et l’autre joueur, des deux pions cyan, lesquels peuvent alors bloquer le pion orange :
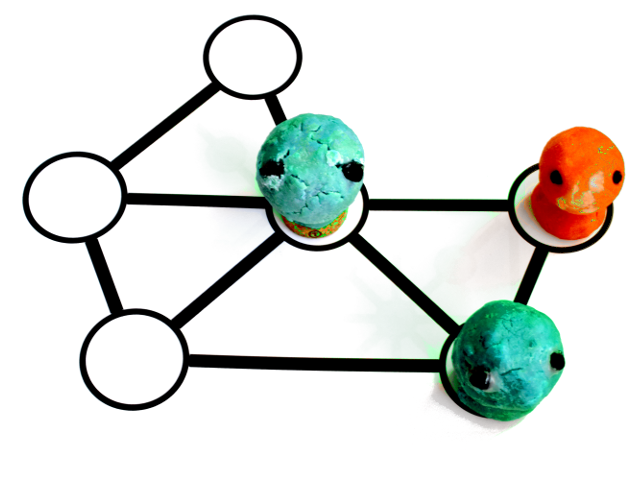
Est-ce que, pour n’importe quelle position de départ des 3 pions, celui qui a les pions cyan va nécessairement gagner le jeu ? Ou est-ce qu’au contraire le pion orange peut obtenir une partie nulle en obligeant les pions cyan à répéter le même mouvement ?
Quoiqu’il en soit, si, à l’âge de 4 ans, il est difficile d’inventer seul ce genre de jeu (des conseils du tonton et l’émulation de la grande sœur ont été utiles) à cause de problèmes de vision des zones du graphe (lignes), le plaisir de la création de jeu et celui de la manipulation des pions sont bel et bien présents à cet âge !
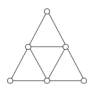
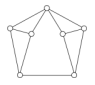
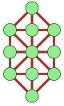
Les graphes ci-dessous ont été créés pour y jouer à des jeux où on peut bloquer l’adversaire, chaque joueur ayant ses pions ; on peut néanmoins s’en servir pour chacune des activités proposées ci-dessus :
| fer à cheval | madelinette | chiens et tang | 2 parkings |
| chaque joueur a 2 pions et il ne reste qu’un sommet vide où on puisse bouger un pion | chaque joueur a 3 pions et il ne reste qu’un sommet vide où on puisse bouger un pion | le jeu du lièvre et du chien est un classique | chaque joueur a 3 pions mais au lieu de bloquer l’adversaire on peut mener ses pions aux sommets diamétralement opposés |
Les trois premiers des jeux ci-dessus ont été décrits par Édouard Lucas dans ses récréations mathématiques. Il semble même que Lucas soit le créateur de la madelinette. Un jeu similaire, présenté à la fête de la science 2017 est celui de Lewthwaite.
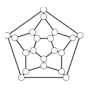
Pour la fête de la science 2016 et la semaine des maths 2017, ont été ajoutés ces deux autres graphes non orientés, originaires de Madagascar :
| le jeu d’Ovide | fanorona-dimy |
| le premier qui a réussi à aligner ses trois pions a gagné | le but du jeu est de prendre tous les pions de l’adversaire [3], par approche ou par éloignement |
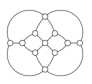
Et plus récemment une extension du jeu des deux parkings :
Jouer à modifier ou créer des graphes
Ces graphes ont été dessinés une fois pour toutes, et même si on veut les colorier il est possible de le faire de façon réversible, en posant des jetons de couleur sur les sommets du graphe. D’autres jeux, plus « papier-crayon », sont basés sur la construction (ou, dans un cas, la destruction) du graphe, arête par arête. Par exemple bridg-it où on construit des ponts. En fait ce jeu est un cas particulier du switching game de Shannon, la construction d’un pont bleu ayant pour effet de couper la route aux elfes rouges.
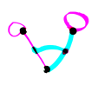
Le jeu de Sprouts est un jeu « papier-crayons » (un crayon par joueur) qui se joue sur une feuille initialement blanche. Enfin presque puisqu’elle contient n points (ci-dessous n=0). Ce sont n sommets (actuellement de degré 0) d’un futur graphe que le jeu consiste à construire. Alors chaque joueur à son tour va
- ajouter une arête
- soit reliant un sommet à lui-même (son degré augmente alors de 2 unités)
- soit reliant deux sommets distincts (leur degré augmente alors d’une unité chacun)
- ajouter sur la nouvelle arête un sommet (de degré 2).
Mais aucun sommet ne doit jamais avoir un degré supérieur à 3 et aucune arête ne doit jamais croiser une autre arête (ni elle-même). Le premier joueur qui ne peut plus tracer d’arête sans violer une de ces règles, est le perdant du jeu.
Voici une feuille permettant de jouer à Sprouts avec n=3 sans avoir à tracer les 3 points avant le jeu :
Fabriquer des graphes avec Nirina974
Le logiciel Nirina974 possède notamment un lien vers les graphes non orientés. La page s’ouvre avec un graphe prédéfini dont on n’aperçoit pas forcément qu’il est planaire :
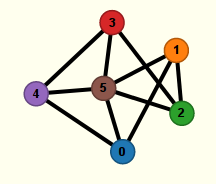
Pour modifier le graphe, on peut
- cliquer quelque part sur le graphe (ou à côté ; mais ailleurs que sur un sommet) ce qui fait apparaître un nouveau sommet (automatiquement nommé par le nombre de sommets créés) ;
- Appuyer sur le bouton Control, puis, sans relâcher celui-ci, cliquer sur une arête (ce qui permet ensuite de la supprimer avec le bouton Suppr)
- Effectuer un Control-clic du même genre que ci-dessus mais sur un sommet, ce qui permet ensuite de le supprimer par Suppr ou de changer sa couleur par p (comme « plus ») ou m (comme « moins »)
- Appuyer sur le bouton Control, puis, sans le lâcher, cliquer sur un sommet, et sans lacher le bouton gauche de la souris, glisser celle-ci de manière à bouger le sommet [4] :
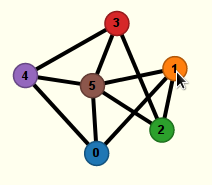
Ci-dessus c’est le sommet 1 qui est en cours de déplacement, en continuant à le tirer par Control-cliquer-glisser vers le bas de la page, on finit par avoir cette version du graphe :
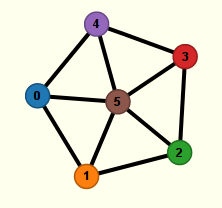
Pour créer un sommet, on clique donc sur la partie vide de la feuille de travail :

Comme il y a déjà 6 sommets sur le graphe, nommés, dans l’ordre, 0, 1, 2, 3, 4 et 5 (le sommet sélectionné, en marron), le sommet nouvellement créé s’appelle 6. Pour continuer la construction du graphe, il est temps de rajouter une arête entre, disons, les sommets 1 et 6. Pour cela, on part de l’un de ces sommets (le 1 ici) puis, en cliquant dessus et en glissant la souris, sans lâcher le bouton gauche, il apparaît une arête provisoire qui est reliée, d’un côté, au sommet, de l’autre côté, à la souris :
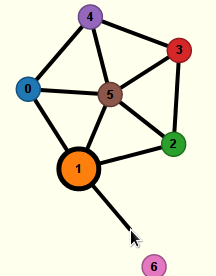
Si on lâche le bouton gauche de la souris alors que celle-ci n’est pas au-dessus d’un sommet, aucune arête n’est créée, et il faut tout recommencer à l’étape précédente. Mais si on lâche le bouton gauche de la souris alors qu’elle est au-dessus du sommet 6, une nouvelle arête est créée, et elle relie les sommets 1 et 6 :
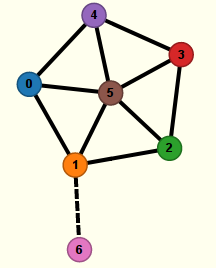
Cette arête est sélectionnée comme si on avait Control-cliqué dessus, ce qui se voit au fait qu’elle est dessinée en pointillés. En sélectionnant le sommet 5 (en cliquant dessus) on voit que l’arête, maintenant désélectionnée, est de même nature que les autres arêtes :
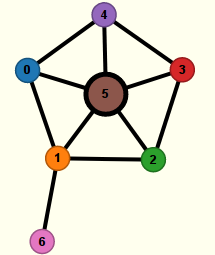
Jouer à Col sur Nirina974
Une fois le graphe créé, on peut cliquer sur le bouton Col en haut à droite, pour passer en mode jeu :

Comme le jeu consiste à colorier des sommets, ils sont devenus blancs :

Un message dit que c’est au tour du joueur « Bleu » de jouer. En effet, les deux joueurs portent en guise de pseudonyme, les noms des couleurs qu’ils utilisent pour remplir les sommets de leurs choix. Comment ? En cliquant sur un sommet
- actuellement blanc
- non adjacent à un sommet déjà colorié dans la même couleur (ici, le bleu) auparavant.
Bleu décide de colorier le sommet 6 :

Le message dit alors que c’est à Rouge de jouer. Rouge décide de colorier le sommet 1 :
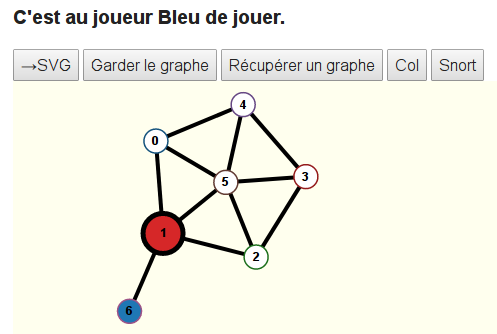
C’est donc à Bleu de jouer. Mais Bleu ne peut colorier ni le sommet 1 ni le sommet 6 qui sont déjà coloriés ; il décide de colorier le sommet 0 :
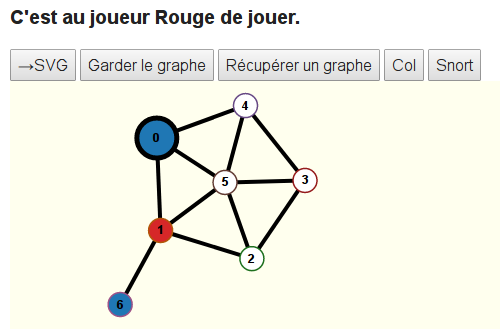
Le message dit que c’est à Rouge de jouer. Les sommets 0,1 et 6 étant déjà coloriés, il ne reste plus que 4 choix ; en réalité 2 car les sommets 2 et 5 étant adjacents à un sommet rouge ne peuvent plus être coloriés en rouge. Seuls les sommets 3 et 4 respectent la double contrainte de n’être ni déjà coloriés, ni adjacents à un sommet rouge. Rouge choisit de colorier le sommet 4 :

C’est donc à Bleu de colorier en bleu un des sommets 2 et 3 (le sommet 5, adjacent à un sommet bleu, est injouable). Il choisit le sommet 3 :

Le texte dit que c’est à Rouge de jouer, mais il ne reste que les sommets 2 et 5 qui sont chacun adjacent à un sommet rouge : Rouge est censé jouer mais ne peut pas jouer. Que se passe-t-il alors ? Rouge a perdu !
Pour rejouer à Col (ou jouer à Snort) il est nécessaire de revenir en mode édition, en cliquant à nouveau sur le bouton Col.
Si on préfère jouer contre la tablette plutôt qu’avoir à passer la tablette d’un joueur à l’autre, Android permet de jouer à Col et Snort
Jouer à Snort sur Nirina974
Une fois en mode édition, on peut démarrer une partie de Snort en cliquant sur le bouton Snort :
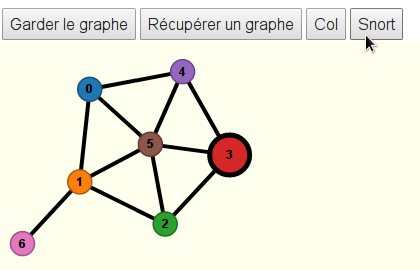
Comme le jeu consiste à colorier des sommets, ceux-ci sont tous blancs au début du jeu. L’un des joueurs s’appelle Bleu et colorie (d’un clic) les sommets en bleu, l’autre joueur, appelé Rouge, colorie les sommets en rouge. Comme l’indique le texte, c’est à Bleu de commencer le jeu. Bleu va donc cliquer sur un des sommets du graphe pour le colorier en bleu. Il choisit le sommet 0 (en exergue ci-dessous) :
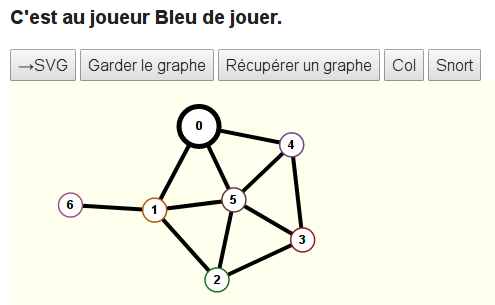
C’est là que Bleu clique, ce qui a pour effet
- de colorier le sommet 0 en bleu
- de changer le nom du joueur en haut :

Bleu passe alors la tablette à Rouge qui peut cliquer sur n’importe quel sommet
- pas encore colorié (le sommet 0 est déjà colorié en bleu donc plus coloriable)
- non adjacent à un sommet bleu : Les sommets 1, 4 et 5 doivent servir de zones-tampon entre les territoires bleu et rouge.
Rouge choisit alors le sommet 2 :
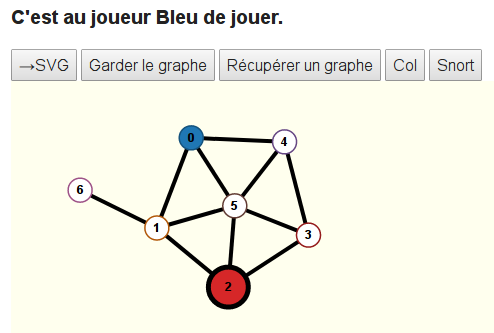
Le texte indique que Rouge doit repasser la tablette à Bleu qui ne peut maintenant plus colorier que l’un des sommets 4 et 6 (tous les autres sommets sont rouges ou adjacents à au moins un sommet rouge). Il choisit le sommet 4 :
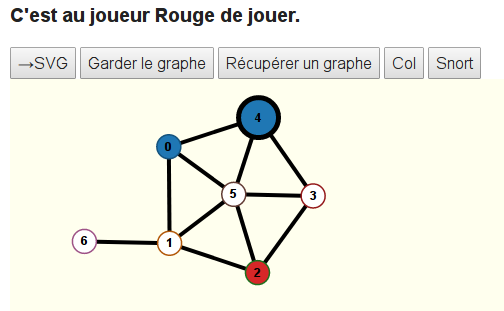
C’est maintenant au tour de Rouge de choisir quel sommet il va colorier. Il colorie le sommet 6 :
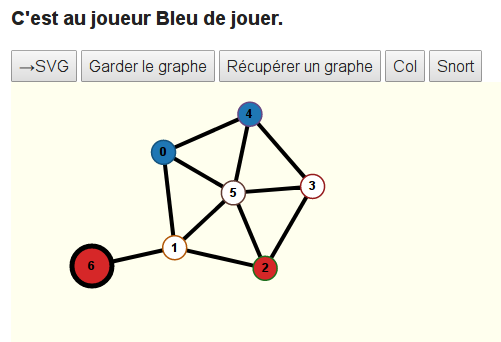
C’est à nouveau au joueur Bleu de jouer, mais s’il joue le 1, que se passe-t-il ?
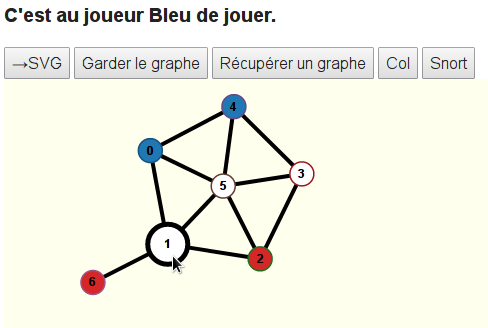
Rien ! Bon sang mais c’est bien sûr : Le sommet 1 est adjacent au sommet 2 qui est rouge, et Bleu ne peut donc pas le jouer. Ce serait contraire à la règle du jeu de Snort. De fait, quoique fasse Bleu, il ne se passera rien, Bleu ne peut plus jouer alors que pourtant c’est à son tour de jouer : Bleu a perdu le jeu.
Graphes orientés
Voici un nouveau graphe orienté pour jouer à Nim :
Comment joue-t-on sur un graphe orienté ?
Les graphes orientés sur lesquels on joue à Nim sont particuliers :
- L’un des sommets, appelé départ, a un degré entrant nul (on ne peut y mener le pion) ;
- Il y a au moins une arrivée qui est un sommet de degré sortant nul (une fois que le pion y est, il ne peut plus bouger).
Pour jouer à Nim sur un graphe orienté muni d’un départ et au moins une arrivée [5],
- On place le pion (commun aux deux joueurs) sur le départ ;
- Chaque joueur à son tour déplace le pion
- depuis le sommet où il se trouve
- vers un sommet adjacent libre
- en suivant le sens de la flèche.
Le premier qui ne peut plus bouger le pion, parce que celui-ci est à l’arrivée , perd le jeu de Nim.
La simplicité du graphe ci-dessus permet d’analyser le jeu à la recherche d’une stratégie gagnante et de découvrir cette notion. Un graphe similaire est ici et un autre, plus complexe mais esthétiquement intéressant, est ici.
Les jeux de Nim suivants ont été présentés dès la fête de la science 2015 :
| jeu de la soustraction | jeu « soustrais un carré » | nim sur triangle | nim sur rectangle |
Créer ses graphes orientés avec Nirina974
En allant sur la page des graphes orientés on voit un graphe déjà commencé :
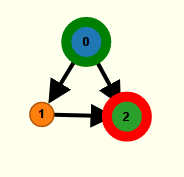
Les sommets numéros 0 et 2 sont plus gros que les autres, parce que ce sont le départ et une arrivée du graphe. Ensuite, dès qu’on clique quelque part sur le graphe, il naît à l’endroit du clic, un nouveau sommet :

Par contre si on ne lâche pas le bouton de la souris après avoir cliqué sur un sommet existant, il se crée une arête qui suit, tant que son bouton gauche reste enfoncé, la souris :
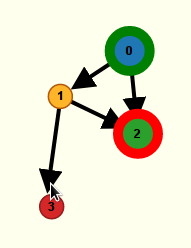
Cette arête disparaît si on lâche le bouton gauche de la souris en dehors d’un sommet, sinon le sommet ainsi sélectionné se voit relié au sommet d’où est parti ce mouvement de cliquer-glisser :

On voit que le sommet 3 est devenu une arrivée, il est donc dessiné plus gros et cerclé de rouge. L’arête qui vient d’être créée est en pointillés pour signifier qu’elle a été sélectionnée. Pour sélectionner une autre arête, il ne faut pas cliquer dessus ! En effet on a vu que cela créerait un nouveau sommet. En fait pour sélectionner un sommet ou une arête, il faut appuyer sur le bouton Control (ou la pomme) et, sans lâcher ce bouton, cliquer sur l’objet que l’on veut sélectionner. Sélectionner un sommet sert, le plus souvent, à le supprimer (avec la touche suppr) puisque, comme on l’a vu, chaque fois que l’on clique par erreur sur un objet, on voit naître un nouveau sommet [6].
Jouer à Nim sur Nirina974
Si on veut jouer à Nim sur le graphe orienté créé dans le tutoriel ci-dessus, il suffit de cliquer sur le bouton jouer :
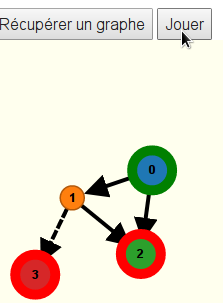
Le clic sur une arête ne va maintenant plus provoquer l’apparition de sommets supplémentaires mais sélectionner l’arête, ce qui peut faire bouger le pion. Le pion est visible en noir sur le sommet de départ et au-dessus du graphe, on peut lire le nom du joueur qui doit cliquer sur l’arête de son choix :
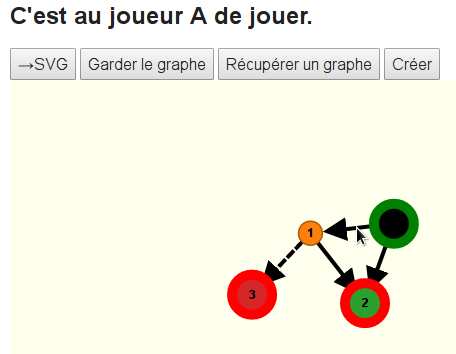
S’il clique sur l’arête en pointillés (celle qui était sélectionnée à l’étape de construction du graphe) cela n’aura aucun effet, car le pion n’est pas au départ de cette arête. Mais si A clique sur l’arête visée ci-dessus, on voit que non seulement le pion a bougé, mais aussi que c’est à B de jouer le coup suivant :
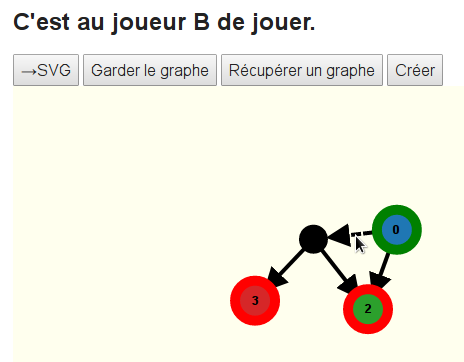
Quoiqu’il joue, il gagne puisque le pion ira à une arrivée. Pour recommencer à jouer, il faut momentanément revenir au mode création :
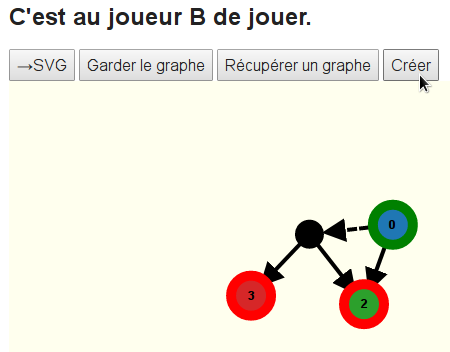
Après cela, un nouveau clic sur jouer remettra le pion au départ, et ce sera à nouveau au joueur A de jouer.
Les jeux d’Aviezri Fraenkel
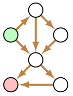
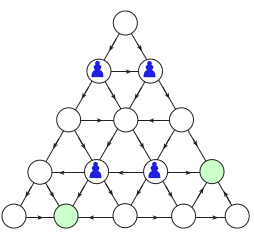
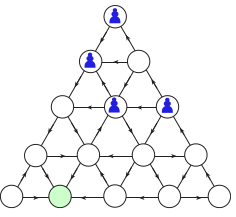
Pour jouer à un jeu de type Nim, il faut un graphe orienté acyclique, en anglais DAG (« Directed Acyclic Graph »), d’où le nom de Doug donné au jeu ci-dessous (« beat Doug on a DAG ») :
Pour jouer à Doug, on place plusieurs pions (ou plutôt des jetons, superposables) sur des positions initiales qui ne sont pas nécessairement des départs. Chaque joueur bouge un des jetons en suivant une flèche, et plusieurs jetons peuvent cohabiter pacifiquement sur un même sommet. Lorsque les 4 jetons sont sur les sommets verts (arrivées, ou « puits » dans le langage des réseaux de flot, ou trou noir chez Fraenkel) le jeu est terminé. Celui qui devait bouger un des jetons a alors perdu la partie. Pour connaître la stratégie gagnante, la notion de nimber s’avère nécessaire, parce qu’il y a plusieurs jetons. Une fois maîtrisée, cette notion permet de « battre Doug » sur n’importe quel DAG, en particulier ceux présentés ci-dessus.
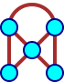
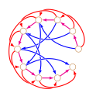
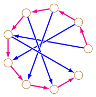
Si le graphe comporte un ou plusieurs cycles, il devient un Cyclic Graph et Fraenkel fait alors appel à Craig :
Dans le graphe cyclique ci-dessus (« Craig ») il n’y a qu’un seul trou noir, le jeu se termine donc lorsque les 4 jetons sont dans ce trou noir. S’il se termine ! En effet s’il ne reste qu’un jeton encore déplaçable sur le graphe, et que ce jeton est tout en bas à droite, il peut accomplir une ronde sans fin autour de ce sommet (le fameux cycle du graphe) et le jeu est déclaré partie nulle ou ko (go). Malgré cela, il y a une stratégie gagnante pour le premier joueur.
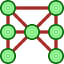
Il en est de même pour ce plus grand Craig, avec 5 corps célestes (les jetons) gravitant autour de 3 « puits gravitationnels » :
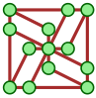
La recherche d’une stratégie gagnante est encore (beaucoup) plus difficile si les jetons interagissent ; la variante proposée par Conway est que lorsque deux jetons sont sur un même sommet, ils disparaissent du jeu (la collision les détruit). C’est le cas sur ce graphe à 17 jetons initiaux, inspiré par Shoemaker-Levy 9 :
On remarque qu’il y a 8 « puits gravitationnels », qui peuvent servir de pièges à jetons : Une fois qu’un jetonest dedans, il ne peut plus échapper à l’attaque d’un pion-kamikaze qui viendrait l’annihiler. Voici les questions posées par Aviezri Fraenkel à propos de ce jeu :
- Existe-t-il une stratégie gagnante à ce jeu ?
- Si oui, en existe-t-il une pour laquelle il survivrait plus d’un jeton à la fin de la partie, chacun coincé dans un piège gravitationnel ?
- Si oui, est-il possible que le jeton rouge [7] survive à ce jeu ?
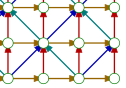
Cela a donné à Aviezri Fraenkel l’idée d’explorer une variante, où, comme aux échecs, si un pion va sur un sommet déjà occupé, c’est l’ancien occupant qui disparaît du jeu (il a été « pris ») mais pas l’attaquant. Ce jeu, appelé arrows parce que le graphe est partiellement orienté, a été commercialisé par Aviezri Fraenkel et Frank Eggleton en 1976, avec des billes de verre et de métal dans un plateau similaire à celui du solitaire :
Dans la version papier, il y a 7 sommets bleus où placer les jetons bleus au début du jeu, et 7 sommets rouge où placer les jetons rouges :
Chaque joueur à son tour déplace un des jetons de sa couleur, depuis le sommet où il se trouve, jusqu’à un sommet adjacent
- en suivant la flèche s’il y en a une
- dans le sens de son choix sinon
et si le sommet d’arrivée est déjà occupé par un jeton de la couleur adverse, celui-ci est retiré du jeu. Attention : On ne peut pas amener un jeton vers un sommet déjà occupé par un jeton de la même couleur (comme aux échecs !). Le but du jeu est de prendre tous les jetons de l’adversaire.
Pour aller plus loin
On peut aussi jouer, sur les graphes orientés, à des jeux de semaille :
| awale généralisé | le source de l’article |
et une autre généralisation des graphes orientés est les réseaux de Petri, sur lesquels on peut jouer comme ci-dessus, chaque joueur effectuant une transition du réseau de Petri jusqu’à ce que ce ne soit plus possible.
| article sur Petri | source en LaTeX |













Commentaires