Pondichéry
Le sujet comportait, en exercice 4, un programme de calcul, et en exercice 5, un calcul de π par la méthode de Monte-Carlo.
Exercice 4
En fait il y avait deux programmes de calcul et l’objet de l’exercice était essentiellement la recherche des nombres donnant le même résultat avec ces deux programmes.
| Programme A • Choisir un nombre • Soustraire 3 • Calculer le carré du résultat obtenu |
Programme B • Choisir un nombre • Calculer le carré de ce nombre • Ajouter le triple du nombre de départ • Ajouter 7 |
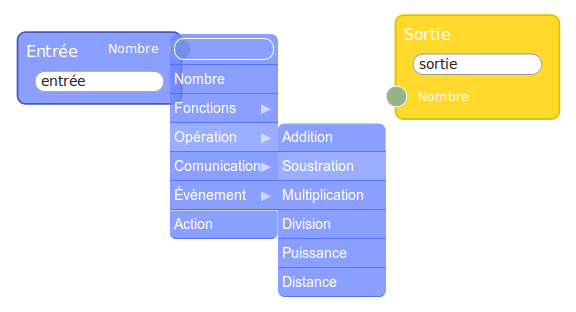
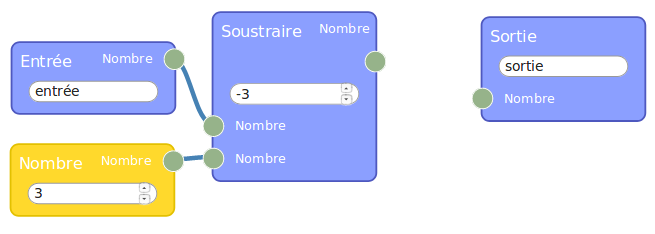
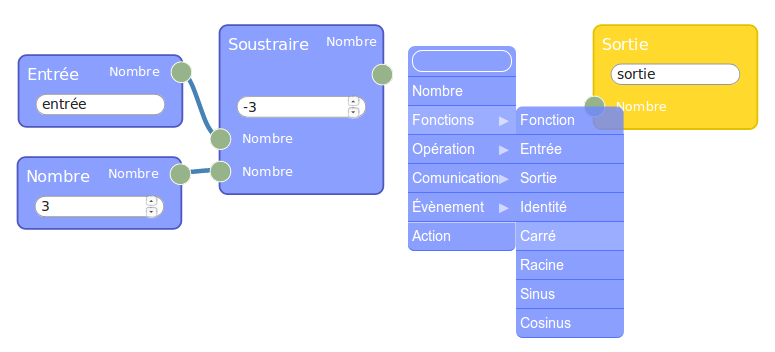
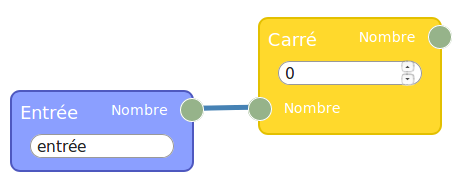
Avant de réutiliser Sofus pour programmer A et B en calcul formel, on va d’abord montrer, sur ces deux programmes, comment mettre en œuvre flow974
Exercice 5
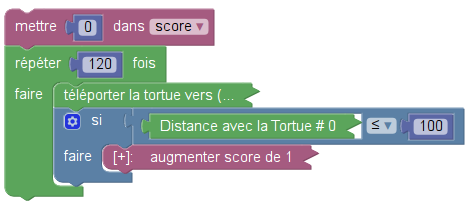
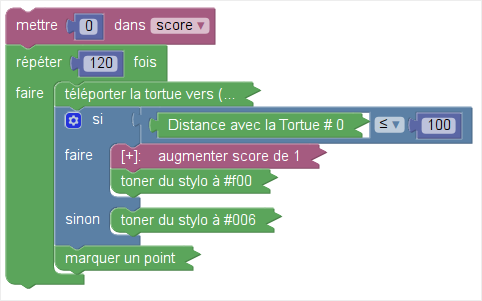
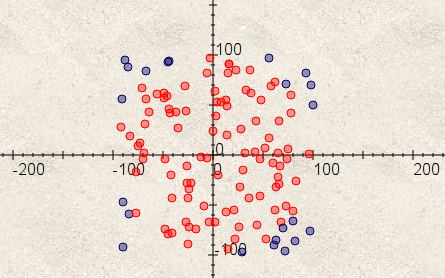
La question 1 portait sur le théorème de Pythagore : Un triangle rectangle était d’ailleurs dessiné sur la copie d’écran de Scratch. La question 2 était une question de cours, portant sur la définition d’un disque. Mais la question 3 s’est montrée très synthétique, en associant le test sur la distance et le calcul de celle-ci par Pythagore. Le script aurait pu être simplifié en laissant Scratch effectuer le calcul de distance et en faisant un dessin à la place. En effet tout lutin de Scratch connaît la distance le séparant d’un autre lutin, et peut s’estampiller sur la scène.
Le script, avec la tortue 0 placée à l’origine du repère, est quand même plus simple que celui de l’énoncé :
USA
Le sujet comportait deux exercices de programmation : Le 4 avec des dessins de carrés par Scratch et le 5, avec un dessin de frise par « un logiciel de géométrie dynamique ».
Exercice 4
L’exercice 4 démarre par la définition d’une procédure « carré ». Le côté du carré est une variable globale côté, comme le montre la version Python ci-dessous, obtenue avec la version péï de SofusPy, et plus précisément la deuxième ligne de la fonction [2] carré() : « global côté » qui explique à Python le caractère global de cette variable.
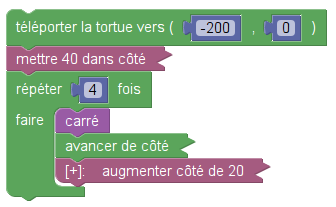
La définition en Blockly est très similaire :

La différence essentielle est que Scratch met le stylo en position d’écriture sans préciser quelle est cette position, alors que Sofus baisse le stylo, la tortue étant vue d’au-dessus, et devant donc baisser son stylo pour que celui-ci laisse une trace de ses mouvements.
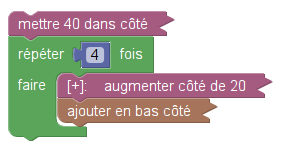
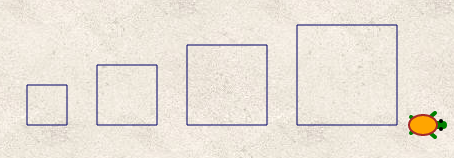
Le script principal montre aussi deux petites différences entre Scratch et Sofus :
- Alors que Scratch met côté à 40, Sofus met 40 dans côté. Ce qui est également suggéré par le pseudocode côté ← 40
- Alors que Scratch ajoute à côté 20, Sofus augmente côté de 20
Par ailleurs il est rappelé dans l’énoncé que s’orienter à 90 (sans unité !) « signifie qu’on se dirige vers la droite » (qui « on » ? Quelle droite ?)
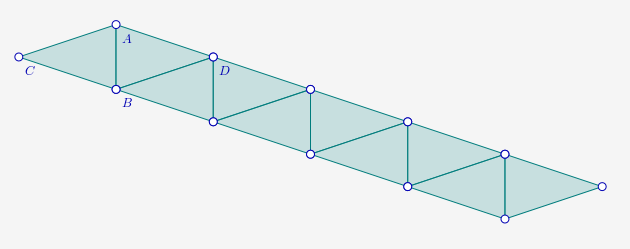
Exercice 5
Le logiciel de géométrie dynamique choisi, est, ici, CaRMetal, parce qu’il permet de programmer la construction de la frise en français.
Étranger
Le sujet comprenait un programme de calcul dans l’exercice 1 (la troisième question d’un « vrai ou faux justifié ») et un programme Scratch à compléter dans l’exercice 6 (la partie B).
Exercice 1
Encore un programme de calcul bourré d’implicites (à qui ajouter 5 ? à qui soustraire 9 ?) :
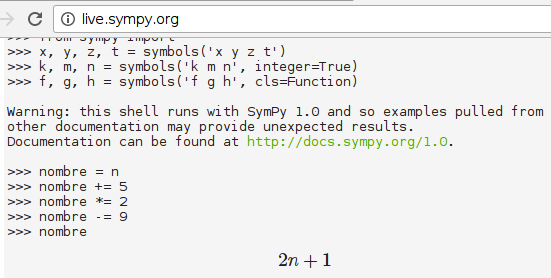
Choisir un nombre;
Ajouter 5;
Multiplier le résultat obtenu par 2;
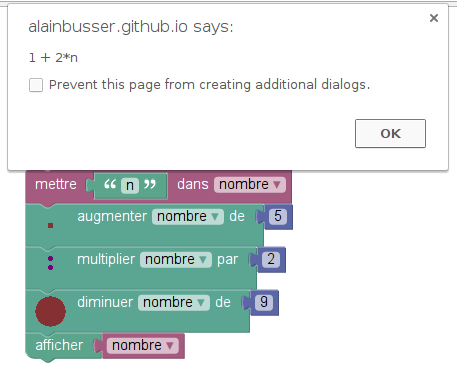
Soustraire 9.On devait dire si la fonction ainsi programmée coïncide avec 2x+1 (x étant le nombre choisi au départ). La réponse affirmative est donnée par Sofus :
Exercice 6
Cet exercice n’est pas une bonne publicité pour Scratch : On dit que le robot est orienté vers le haut alors qu’il doit effectuer des parcours horizontaux dans le champ ; et le « costume » choisi pour le robot dans l’illustration ne le montre pas vu de haut, alors que son tracé est donné en vue aérienne.
On ne sait pas si les élèves doivent dessiner des blocs ou seulement écrire du texte, en tout cas on leur demande clairement d’« écrire un programme simple », même si c’est dans des définitions de fonctions.
Voici le corrigé avec Sofus :
Asie
Un exercice 3 très western avec le dessin dune étoile de sheriff (enfin, à 5 branches).
Remarque : L’énoncé commence par « Arthur doit écrire un programme avec Scratch » ce qui, une deuxième fois, montre que « programmation visuelle par blocs » signifie, quoique de façon officieuse, « Scratch et rien d’autre ». Étant donné que de façon officielle il ne fallait pas former des experts sur un outil particulier, on peut extrapoler au lycée, en imaginant que le langage Python, quoique non annoncé officiellement, sera présent et cité explicitement au bac dans les années qui viennent.
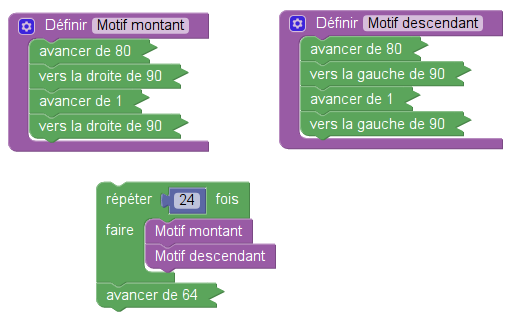
Question 1 : Pour dessiner l’étoile à 5 branches, il faut boucler 5 fois, ce qui n’est pas vraiment surprenant :
On remarque que Sofus, en épurant le script, permet de concentrer l’attention des élèves sur ce qui constitue le cœur du sujet et ne pas les distraire par des considérations hors sujet comme les effets de l’effaçage, les manipulations de stylo ou l’orientation par défaut du lutin/tortue...
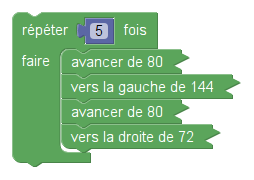
Question 2 : Comme chaque branche de l’étoile est faite de deux parcours de 80 pixels chacun, le préimètre s’obtient en multipliant par 5 la somme 80+80. Là encore, pas de grosse surprise.
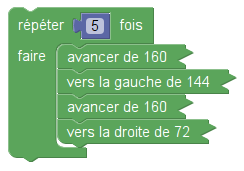
Question 3 : Pour dessiner l’étoile 2 fois plus grande, il faut que chaque longueur soit doublée, ce qui n’est pas vraiment surprenant non plus :
Métropole-Réunion
Le sujet est intéressant ici, pour 2 raisons : L’exercice 5 et son programme de calcul ; et l’exercice 6 avec un dessin fait avec Scratch.
Exercice 5
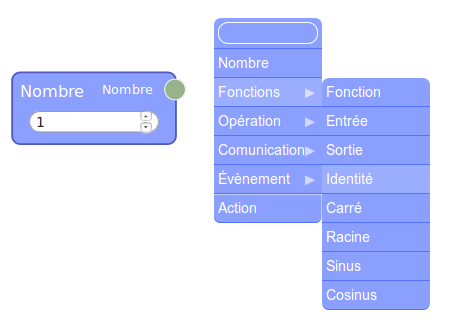
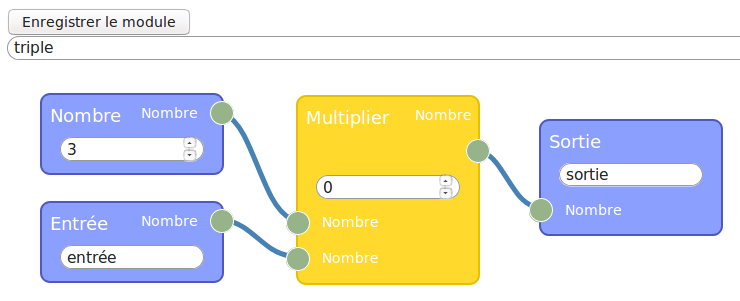
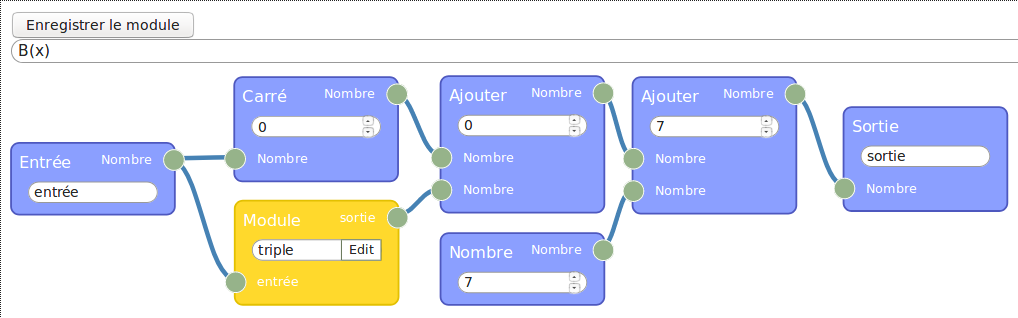
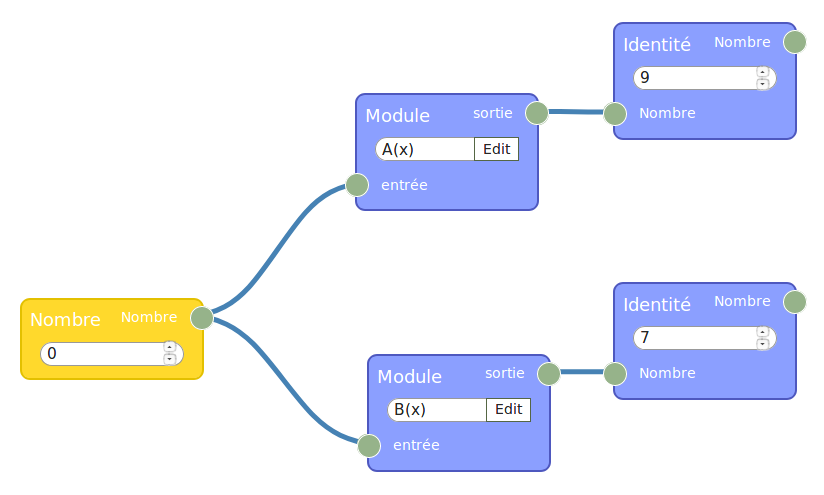
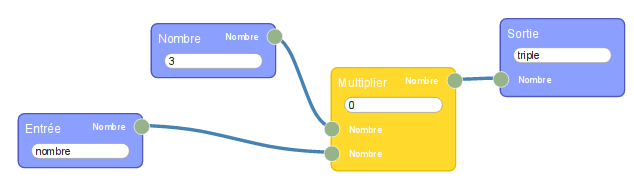
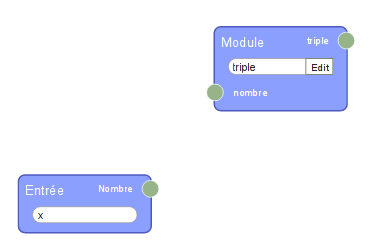
Le programme de calcul est si court qu’on se demande si ça vaut le coup de le placer dans un module de ce genre :
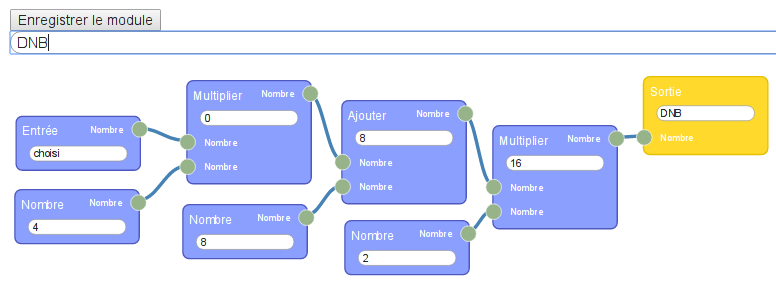
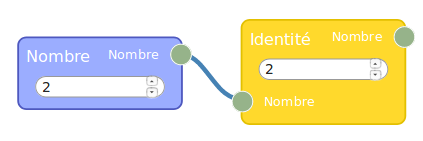
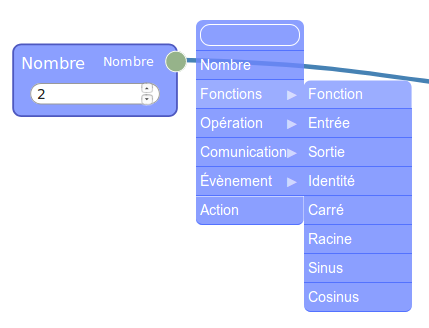
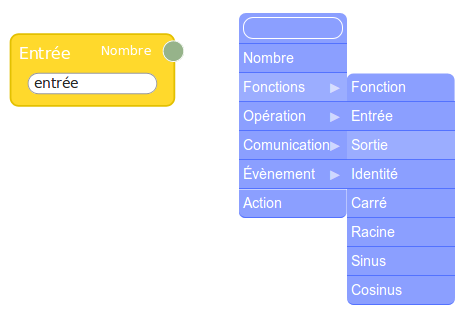
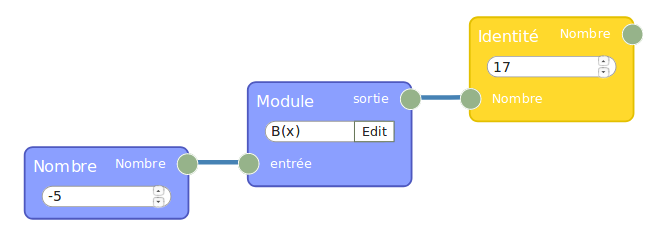
La réponse est oui : Le nombre en entrée est manipulable en dehors du module alors que les autres (variables locales du point de vue de la programmation fonctionnelle) sont constants du point de vue extérieur. L’affichage du résultat par flow974 se fait en utilisant une fonction identité :

On y lit la réponse à la question 1, mais une exploration plus poussée révèle qu’aucune entrée entière ne donne 30 en sortie. On passe donc à Sofus pour la suite :
Exercice 6
L’exercice consistait à dessiner des carrés et des triangles homothétiques avec ces fonctions :
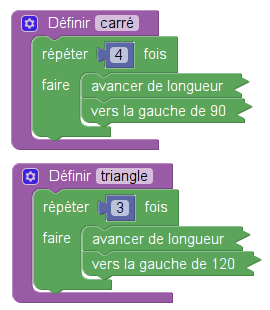
Le script épuré (notamment de l’affectation, inévitable avec Scratch mais pas avec Sofus), donne ceci :
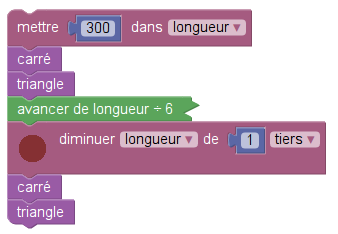
Ce script étant complet, donne un corrigé des questions 1 et 2 (hormis les coordonnées du lutin, qui se calculent par une division de 300 par 6 ; la difficulté n’est pas insurmontable). Pour la question 3, le rapport d’homothétie se calcule en soustrayant 1/3 à 1 et le rapport des aires, en calculant le carré d’une fraction. Là encore, il ne devrait pas y avoir de difficulté majeure.
Polynésie
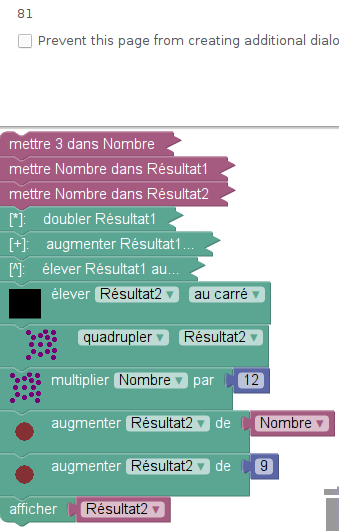
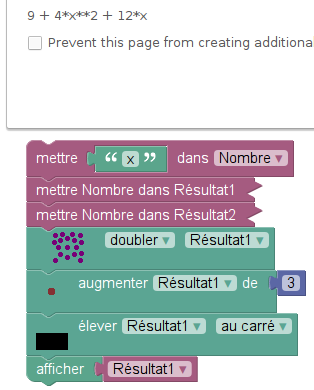
Le sujet se clôt par un exercice comportant un programme de calcul. L’énoncé laisse un peu perplexe, avec « un script saisi par Alice dans un logiciel d’algorithmique ». En effet, un algorithme est défini comme « une suite finie et non ambiguë d’opérations ou d’instructions permettant de résoudre un problème », et là, on a du mal à imaginer un problème dont la solution serait fournie par le script d’Alice. Ensuite, le premier bloc du script demande au lutin d’attendre, ce qui n’est peut-être pas l’action la plus efficace pour résoudre un problème. Une fois l’attente terminée, le lutin envoie un message à tous, c’est-à-dire à lui-même vu qu’apparemment il est seul. Puis il modifie trois variables Nombre, Résultat1 et Résultat2 de manière un peu imprévisible (on dirait un mélange de modifications et d’affectations par des expressions algébriques). On proposera donc ici de tout faire comme programme de calcul (en fait, deux programmes en un) et plutôt que faire demander un nombre par un lutin, affecter directement le Nombre par 3 ou x selon la question.
Question 2 : Généralisation
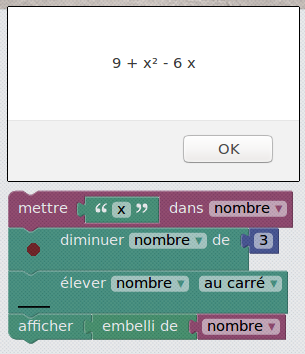
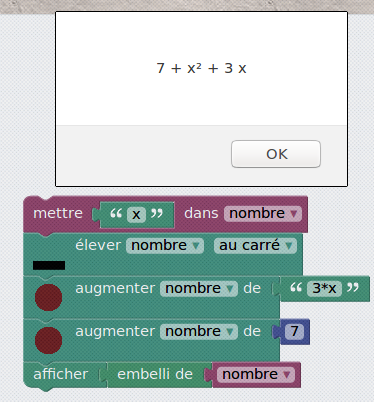
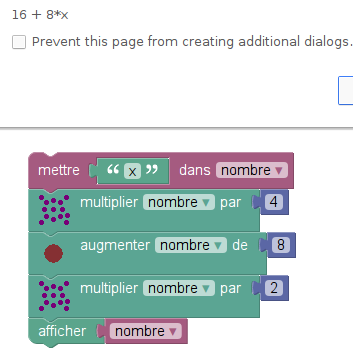
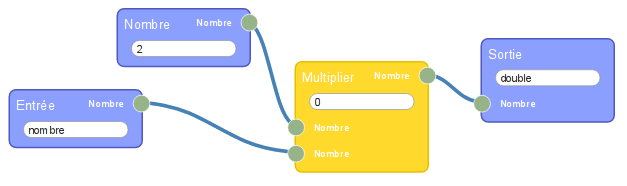
Il suffit, dans un premier temps, de remplacer le nombre 3 par la lettre x dans les scripts précédents :
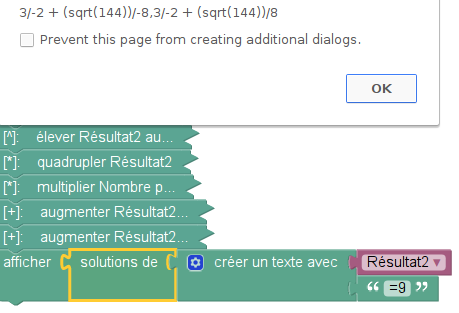
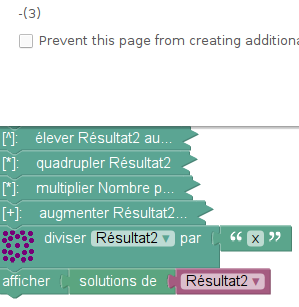
Question c : Quand est-ce que le Résultat2 vaut 9 ?
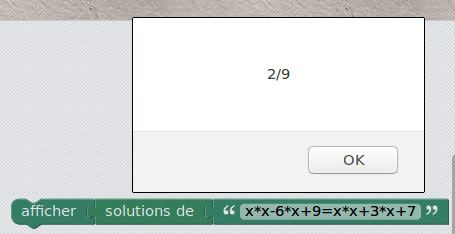
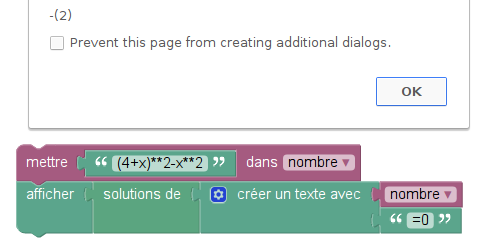
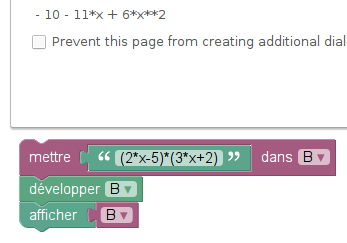
Si, comme dans les questions a et b, on appelle x la valeur initiale du Nombre, la valeur finale de Résultat2 est 4x²+12x+9. Cette expression est une expression (si si !). La fonction à laquelle il est fait allusion dans les questions a et b est une liaison entre les expressions x et 4x²+12x+9. Mais on peut également, à partir de l’exrpession 4x²+12x+9, fabriquer une équation en lui accolant « =9 » :

La question c demande ni plus ni moins que de résoudre cette équation.
Septembre
En Polynésie, Scratch (ou quelque chose de ressemblant) était utilisé pour résoudre une équation par balayage :
Une personne pratique le vélo de piscine depuis plusieurs années dans un centre aquatique à raison de deux séances par semaine. Possédant une piscine depuis peu, elle envisage d’acheter un vélo de piscine pour pouvoir l’utiliser exclusivement chez elle et ainsi ne plus se rendre au centre aquatique.
• Prix de la séance au centre aquatique : 15 €.
• Prix d’achat d’un vélo de piscine pour une pratique à la maison : 999 €.
Le but de l’exercice était de savoir à partir de combien de semaines l’achat du vélo deveint rentable. Avec ce genre de script :

On remarque que la boucle « jusqu’à » a été préférée à l’omniprésente « tant que », ce qui pour ce genre de problème, élimine Python.
Le sujet de Métropole-Réunion-Antilles-Guyane comportait deux exercices sur la programmation : Le 5 avec des tracés de rectangles par Scratch, et le 6 avec un programme de calcul représenté par un graphe orienté, donc totalement propice à une approche par flow974.
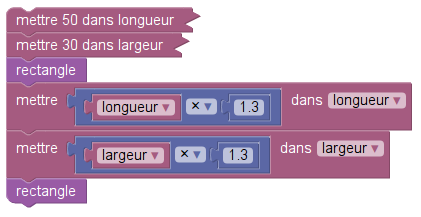
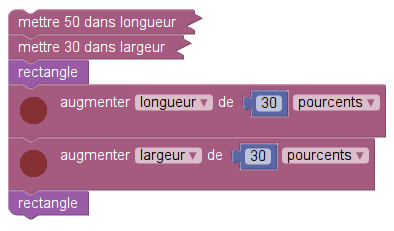
Exercice 5
On remarque que le tracé d’un rectangle est effectué par une procédure (« définition de blocs ») et que les dimensions du rectangle sont des variables globales. Cela s’éloigne d’expériences menées avec Logo où les dimensions étaient fournies à la procédure.
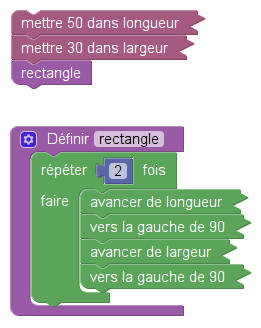
Les dimensions du rectangle sont les variables globales longueur et largeur.

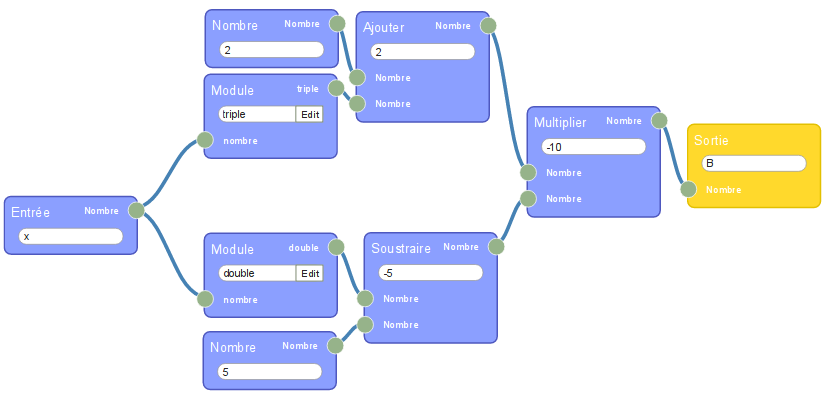
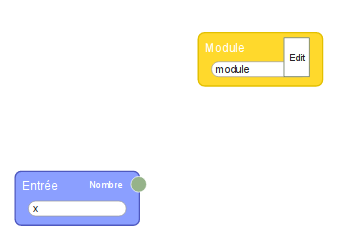
Exercice 6
La version flow974 ressemble quand même beaucoup à l’énoncé :
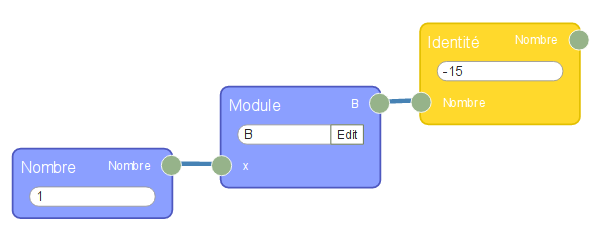
Amérique du Sud
Le sujet comportait deux exercices sur la programmation : Le 3 avec des programmes de calcul, et le 6 avec des frises en Scratch.
Exercice 3
L’exercice portait sur des programmes de calcul (affines) donnant en fait les mêmes réponses pour tout nombre choisi en entrée.
Voici le programme 1 décrit dans l’énoncé :
• Soustraire 5
• Multiplier par 4
et en version flow974 :

et le programme 2, dans l’énoncé :
• Multiplier par 6
• Soustraire 20
• Soustraire le double du nombre de départ
puis en version flow974 [4] :
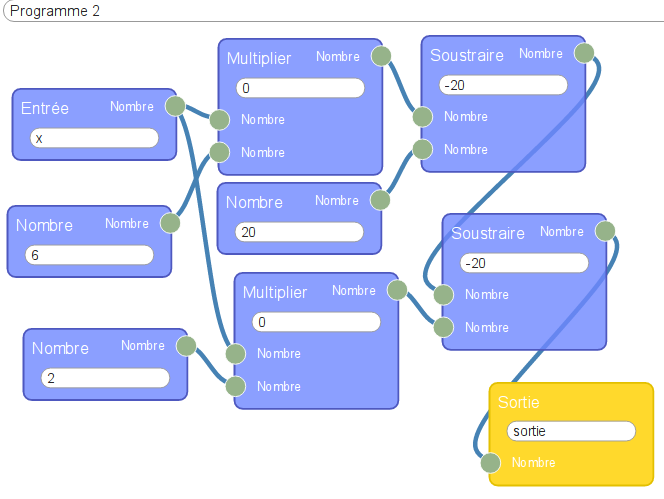
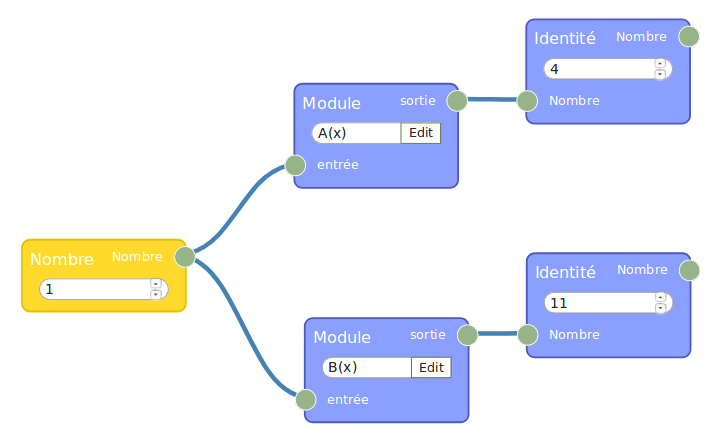
Une fois qu’on a enregistré dans flow974, ces deux fonctions, on peut y entrer un même nombre et faire suivre chacune d’entre elles d’un bloc « identité » (qui affiche le résultat comme le ferait une monade d’haskell) :
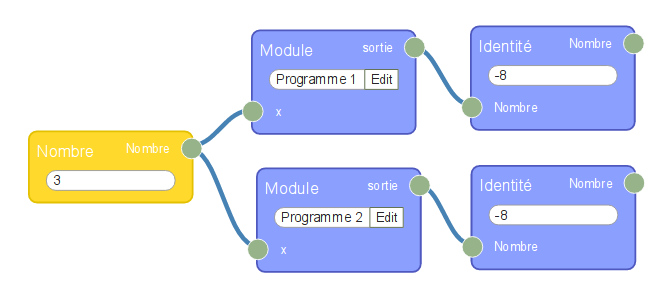
Ensuite, pour répondre à la question 2, il suffit de remplacer le nombre d’entrée par -2 :
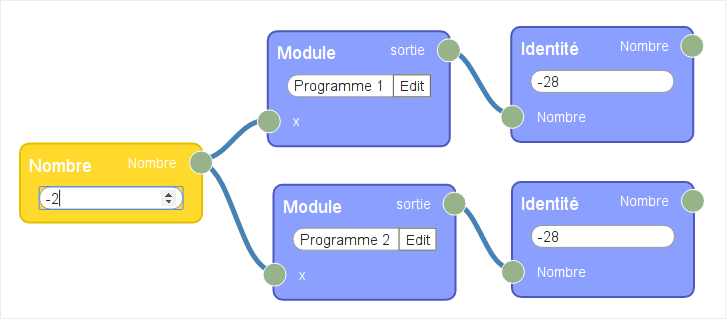
Cela amène à conjecturer que les deux fonctions n’en seraient en réalité qu’une, et la suite de l’exercice consiste à renforcer puis prouver cette conjecture.
Ce n’est pas Scratch qui a été choisi pour réaliser les programmes de calcul, mais le tableur. Pourtant, avec Sofus, on a vite les réponses, surtout si on décide d’appeler x le fameux nombre choisi en entrée :

La version simplifiée du Programme 1 est 4x-20 :
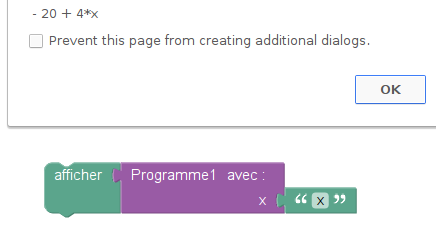
Et la version simplifiée du programme 2 est aussi 4x-20 :
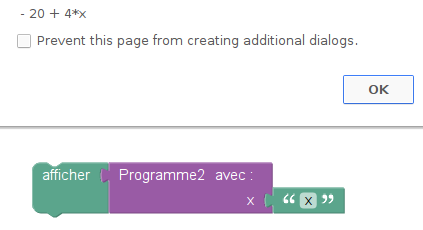
Ce qui prouve la conjecture émise par Lucie.
Exercice 6
Un chat devait dessiner le motif suivant :

La tortue de Sofus semble aussi douée que le chat pour ce faire. Et elle fait ceci :
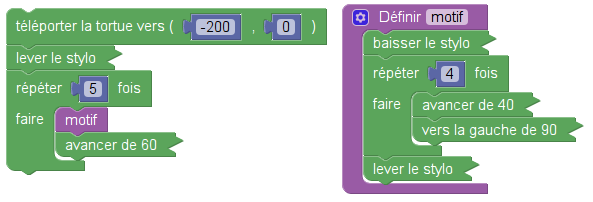
La question portait sur la distance entre les motifs, celle-ci est donc de 60. Et si on avait mis 40, on aurait obtenu ceci :

Pour avoir un motif triangulaire, on pouvait faire ainsi :

Remarquer que la question sur la distance admettait plusieurs réponses correctes, l’objet étant de dessiner un triangle sans que ses dimensions soient précisées. Mais avec les données ci-dessus, on trouve un dessin relativement conforme au début de l’énoncé :
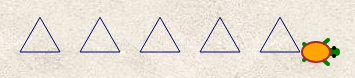
Mais toute valeur multiple de 3 convenait pour a, et toute valeur positive convenait pour b. Seul c devait nécessairement être de 120 (encore qu’en ajoutant un multiple de 360 on ne voyait pas la différence non plus).
Nouvelle-Calédonie
L’exercice 8 du sujet faisait faire des dessins par un chat.
Le script 1 de l’énoncé comportait 7 blocs. La version Sofus n’en comporte que 4 :
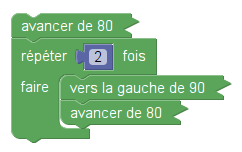
Les deux scripts donnent ce dessin (à faire à la main sur la feuille) :
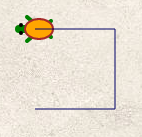
Le script 2 de l’énoncé totalise pas moins de 9 blocs ; la version Sofus n’en prend que 6 :
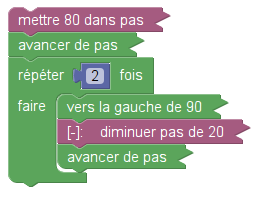
Quels sont les 3 blocs que Sofus permet d’économiser ? Le drapeau vert, l’orientation du lutin au départ, et la gestion du stylo, levé par défaut [5].
Le dessin obtenu est celui-ci :
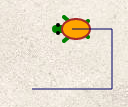
Alors que pour avoir ce dessin :
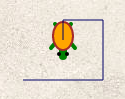
Il fallait ce script :































Commentaires