L’auteur : Géry Huvent est professeur en classes préparatoires PCSI au lycée Faidherbe de Lille.
Son site personnel, Epsilon Maths, est très riche : outre les documents de travail destinés à sa classe, on y trouvera des pages sur le nombre Pi et le nombre Zêta(5), divers articles de mathématiques et quelques sangaku remarquables.

Géry Huvent est, en effet, un passionné de sangaku. On lira avec délectation son ouvrage : Sangaku. Le mystère des énigmes géométriques japonaises, Dunod, 2008. Voici comment l’ouvrage est présenté par l’éditeur :

« Au Japon, les sanctuaires shinto et les temples bouddhistes peuvent renfermer de véritables trésors mathématiques : sur des tablettes de bois accrochées aux auvents, sont peintes des énigmes géométriques colorées, les sangaku. Les sangaku ont vu le jour au cours de la période Edo (1600-1868) quand le Japon avait coupé presque tout contact avec le monde extérieur. Composées de figures simples (cercles, triangles, carrés...) et témoignant du sens de l’esthétisme japonais, ces énigmes présentent une très grande originalité. À travers une sélection des plus beaux et plus intéressants sangaku, classés par difficulté et présentés avec leur solution complète, cet ouvrage vous fera découvrir ce joyau encore mal connu des mathématiques japonaises. »

Géry Huvent ne pouvait rester indifférent au sangaku des cercles inscrits égaux proposé par le hors-série de la revue Tangente sur le cercle. Après avoir pris connaissance des preuves élémentaires publiées dans l’article d’Yves Martin et Dominique Tournès, il a cherché et rédigé la solution par la trigonométrie hyperbolique qui était évoquée par les rédacteurs de Tangente. Nous le remercions chaleureusement pour avoir accepté de publier cette solution en avant-première sur le site de notre IREM. Une version améliorée et enrichie de compléments sera publiée ultérieurement sur son site personnel.

Solution de Géry Huvent

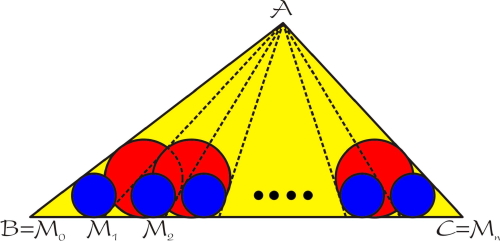
On considère un triangle ABC que l’on partage en n triangles
$AM_{k-1}M_{k},$ $1\leq k\leq n$, de telle façon que les cercles inscrits
à ces n triangles aient tous même rayon. Alors les cercles inscrits
dans les triangles construits par regroupement de deux triangles
consécutifs ont également même rayon.

Pour démontrer ce résultat, on se place dans le repère indiqué
par la figure suivante. L’axe des ordonnées est la droite (BC), l’origine le projeté orthogonal de A sur cette droite. Le point A ayant pour coordonnées (0, h), où $h>0$.

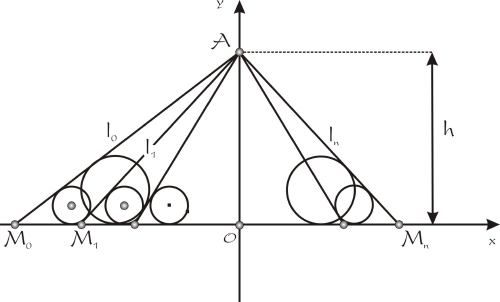
Soit $x_{k}$ l’abscisse du point $M_{k},$ on pose $x_{k}=h\,\text{sh} (t_{k}) $ (ou $t_{k}=\arg\text{sh}(x_{k}/h)$ pour être précis). On note

• $l_{k} =AM_{k}$ ; $a_{k}=M_{k-1}M_{k}$ et $a=M_{0}M_{n}$ ;
• $p_{k} =\dfrac{1}{2} ( l_{k-1}+l_{k}+a_{k})$ est le
  demi-périmètre de $AM_{k-1}M_{k},$ k variant de 1 à n ;
• $\sigma_{k} =\dfrac{1}{2}ha_{k}$ est l’aire de $AM_{k-1}M_{k},$
  k variant de 1 à n ;
• $p =\dfrac{1}{2} ( l_{0}+l_{n}+a)$ est le demi-périmètre de ABC ;
• $\mathcal{A} =\dfrac{1}{2}ha$ est l’aire de ABC ;
• r est le rayon commun des cercles inscrit aux triangles $AM_{k-1}M_{k}$ pour k variant de 1 à n.

Alors

$l_{k} =\sqrt{h^{2}+h^{2}\,\text{sh}^{2}\left( t_{k}\right) }=h\,\text{ch}\left( t_{k}\right) \text{ pour }0\leq k\leq n\ ;$

$l_{k-1}+l_{k} =h\left( \text{ch}\left( t_{k-1}\right) +\text{ch}\left( t_{k}\right) \right) =2h\,\text{ch}\left( \dfrac{t_{k}-t_{k-1}}{2}\right) \text{ch}\left( \dfrac{t_{k} +t_{k-1}}{2}\right)\ ;$

$a_{k} =h\left( \text{sh}\left( t_{k}\right) -\text{sh} \left( t_{k-1}\right) \right) =2h\,\text{sh}\left( \dfrac {t_{k}-t_{k-1}}{2}\right) \text{ch}\left( \dfrac{t_{k}+t_{k-1}} {2}\right)\ ;$

$p_{k} =h\left[ \text{ch}\left( \dfrac{t_{k}-t_{k-1}}{2}\right) +\text{sh}\left( \dfrac{t_{k}-t_{k-1}}{2}\right) \right] \text{ch}\left( \dfrac{t_{k}+t_{k-1}}{2}\right) =h\,\text{ch} \left( \dfrac{t_{k}+t_{k-1}}{2}\right) \exp\left( \dfrac{t_{k}-t_{k-1}} {2}\right).$

On en déduit que

$r =\dfrac{\sigma_{k}}{p_{k}}=\dfrac{1}{2}\,h\dfrac{a_{k}}{p_{k} }=h\,\text{sh}\left( \dfrac{t_{k}-t_{k-1}}{2}\right) \exp\left( -\dfrac{t_{k}-t_{k-1}}{2}\right)$

$\quad \quad =\dfrac{h}{2}\times\left( 1-\exp\left( t_{k-1}-t_{k}\right) \right).$

Cette égalité prouve que la suite $\left( t_{k}\right) _{0\leq k\leq n}$ est arithmétique de raison $\rho=-\ln\left( 1-\dfrac{2r}{h}\right).$ En particulier, on a $t_{k}=t_{0}+k\rho.$

On calcule ensuite le rayon du cercle inscrit au triangle $AM_{k}M_{k+2},$ pour $0\leq k\leq n-2$. On a

$M_{k}M_{k+2}=h\left( \text{sh}\left( t_{k+2}\right) -\text{sh}\left( t_{k}\right) \right) =2h\,\text{sh}\left( \dfrac{t_{k+2}-t_{k}}{2}\right) \text{ch}\left( \dfrac{t_{k+2} +t_{k}}{2}\right) =2h\,\text{sh}\left( \rho\right) \text{ch} \left( \dfrac{t_{k+2}+t_{k}}{2}\right).$

Le demi-périmètre de $AM_{k}M_{k+2}$ est donc

$h\,\text{sh}\left( \rho\right) \text{ch}\left( \dfrac {t_{k+2}+t_{k}}{2}\right) +\dfrac{l_{k+2}+l_{k}}{2}=h\exp\left( \rho\right) \text{ch}\left( \dfrac{t_{k+2}+t_{k}}{2}\right).$

et son aire vaut $\dfrac{1}{2}\,hM_{k}M_{k+2}.$

Le rayon du cercle inscrit à $AM_{k}M_{k+2}$ est bien constant et vaut

$h\,\text{sh} ( \rho) \exp ( -\rho) =\dfrac{h}{2}\, ( 1-\exp (-2\rho) ) =2\,\dfrac{r (h-r)}{h}.$

On peut également exprimer le rayon r en fonction de a, $\mathcal{A}$
et p. Puisque $t_{n}=t_{0}+n\rho,$ on a

$a =2h\,\text{sh}\left( \dfrac{t_{n}-t_{0}}{2}\right) \text{ch}\left( \dfrac{t_{n}+t_{0}}{2}\right) =2h\,\text{sh} \left( \dfrac{n\rho}{2}\right) \text{ch}\left( \dfrac{t_{n}+t_{0} }{2}\right)$

$p =h\left[ \text{ch}\left( \dfrac{t_{n}-t_{0}}{2}\right) +\text{sh}\left( \dfrac{t_{0}-t_{n}}{2}\right) \right] \text{ch}\left( \dfrac{t_{n}+t_{0}}{2}\right) =h\,\text{ch} \left( \dfrac{t_{n}+t_{0}}{2}\right) \exp\left( \dfrac{t_{n}-t_{0}} {2}\right) =h\,\text{ch}\left( \dfrac{t_{n}+t_{0}}{2}\right) \exp\left( \dfrac{n\rho}{2}\right)$

$\mathcal{A} \mathcal{=}\dfrac{1}{2}\,ha=h^{2}\,\text{sh}\left( \dfrac{n\rho}{2}\right) \text{ch}\left( \dfrac{t_{n}+t_{0}} {2}\right),$

d’où

$\dfrac{\mathcal{A}}{p} =h\,\text{sh}\left( \dfrac{n\rho}{2}\right) \exp\left( -\dfrac{n\rho}{2}\right) =\dfrac{h}{2}\left( 1-\exp\left( -n\rho\right) \right)$

$\quad \quad =\dfrac{h}{2}\left( 1-\left( 1-\dfrac{2r}{h}\right) ^{n}\right).$

Avec $\mathcal{A=}\dfrac{1}{2}\,ah,$ on déduit

$\dfrac{2\mathcal{A}}{hp} =\dfrac{a}{p}=\left( 1-\left( 1-\dfrac{2r} {h}\right) ^{n}\right) \Longrightarrow \boxed{\left( 1-\dfrac{a}{p}\right) ^{1/n}=1-\dfrac{2r}{h}}$

d’où $r =\dfrac{h}{2}\left( 1-\left( 1-\dfrac{a}{p}\right) ^{1/n}\right)$

ce qui s’écrit $\boxed{r=\dfrac{\mathcal{A}}{a}\left( 1-\left( 1-\dfrac{a}{p}\right) ^{1/n}\right)}\,.$

On peut généraliser facilement et calculer le rayon du cercle inscrit
au triangle $AM_{i}M_{i+k}$, pour constater qu’il est constant. Soit $r_{i}$
ce rayon, on calcule donc

$M_{i}M_{i+k} =h\left( \text{sh}\left( t_{i+k}\right) -\text{sh}\left( t_{i}\right) \right) =2h\,\text{sh}\left( \dfrac{t_{i+k}-t_{i}}{2}\right) \text{ch}\left( \dfrac{t_{i+k} +t_{i}}{2}\right) =2h\,\text{sh}\left( \dfrac{k\rho}{2}\right) \text{ch}\left( \dfrac{t_{i+k}+t_{i}}{2}\right)$

$l_{i}+l_{i+k} =2h\,\text{ch}\left( \dfrac{k\rho}{2}\right) \text{ch}\left( \dfrac{t_{i+k}+t_{i}}{2}\right).$

Le demi-périmètre du triangle $AM_{i}M_{i+k}$ vaut ainsi

$\dfrac{1}{2}\left( M_{i}M_{i+k}+l_{i}+l_{i+k}\right) =h\,\text{ch} \left( \dfrac{t_{i+k}+t_{i}}{2}\right) \exp\left( \dfrac{k\rho}{2}\right)$

et son aire est $\dfrac{1}{2}\,h\,M_{i}M_{i+k}.$ Le rayon $r_{i}$ a donc pour valeur

$r_{i}=h\,\text{sh}\left( \dfrac{k\rho}{2}\right) \exp\left( -\dfrac{k\rho}{2}\right) =\dfrac{h}{2}\left( 1-\exp\left( -k\rho\right) \right) =\dfrac{h}{2}\left( 1-\left( 1-\dfrac{2r}{h}\right) ^{k}\right).$

Puisque $1-\dfrac{2r}{h}=\left( 1-\dfrac{a}{p}\right) ^{1/n}$, on en déduit que

$r_{i}=\dfrac{h}{2}\left( 1-\left( 1-\dfrac{a}{p}\right) ^{k/n }\right) =\dfrac{\mathcal{A}}{a}\left( 1-\left( 1-\dfrac{a}{p}\right) ^{k/n}\right).$