Le problème des anniversaires

Le problème des anniversaires est un problème connu, sa résolution est un exercice simple de combinatoire.

Dans cette activité, présentable à tous les niveaux du lycée hormis le calcul de la probabilité qui ne s’adresse qu’à un élève de Terminale scientifique, on va considérer trois aspects : celui de la simulation de l’expérience aléatoire sur Excel, puis celui de la simulation sur TI 83 qui va nous donner l’occasion de proposer un algorithme qui va s’inscrire dans le chapitre « algorithmique » du nouveau programme de Seconde, la traduction de cet algorithme en un programme sur TI 83 et enfin le calcul de la probabilité.

Problème : dans une classe de 28 (par exemple) élèves, quelle est la probabilité pour que deux élèves aient la même date d’anniversaire ?

L’expérience aléatoire se modélise ainsi : parmi tous les tirages aléatoires de 28-listes de nombres pris entre 0 et 364, quelle est la probabilité de ne pas obtenir une liste de nombres tous distincts ?

Simulation de l’expérience aléatoire sur Excel

• Dans la cellule A1 on entre la formule « =ENT(365*ALEA()) » et on « tire » jusqu’à la cellule AB1, on a ainsi simulé 28 jours de naissance parmi 365, de façon aléatoire.
• On sélectionne ensuite les cellules A1 à AB1 puis on « tire » jusqu’à la ligne 1000 ; on a ainsi simulé 1000 fois 28 jours de naissance parmi 365, de façon aléatoire.
• Dans la cellule AD1 on entre la formule « =NB.SI($A1 :$AB1 ;A1) » qui calcule le nombre d’apparitions de la cellule A1 dans la plage A1à AB1, le $ étant là pour que la plage reste la même quand « on tire » la cellule AD1 jusqu’à la cellule BE1, ce que l’on fait. On vient donc, dans la plage AD1 à BE1 de calculer le nombre d’apparitions des cellules de la plage A1à AB1 dans cette même plage.
• On sélectionne la plage AD1 à BE1 et « on tire » jusqu’à la ligne 1000, on a donc fait le calcul précédent pour chacune des 1000 simulations.
• Dans la cellule BG1 on entre la formule « =MOYENNE(AD1:BE1) » qui calcule la moyenne de la plage AD1à BE1, ceci dans le but de faire le test : les cellules de la plage A1 à AB1 sont elles distinctes deux à deux ou non ? Ce qui va ce traduire par : cette moyenne est elle égale à 1 ou non ?
• « On tire » la cellule BG1 jusqu’à la cellule BG1000.
• En BH1 on entre la formule « =SI(BG1=1 ;1 ;0) » qui entre 1 si BG1=1 et 0 sinon. « On tire ensuite BH1 jusqu’à BH1000, la moyenne de la colonne BH va alors être la fréquence (probabilité) de l’événement contraire de l’événement qui nous intéresse.
• En BJ1 on entre la formule « =1-MOYENNE(BH1:BH1000) » qui fait le calcul décrit
  ci- dessus. En appuyant plusieurs fois sur F9, ce qui a pour effet de faire varier l’échantillon, les résultats tournent autour de 0.65.

Simulation de l’expérience aléatoire sur TI83

On va faire un programme sur TI83 qui va simuler l’expérience décrite plus haut.
L’algorithme est le suivant :

• On saisit le nombre N d’expériences aléatoires.
• On saisit le nombre P d’élèves, P=28 ici mais pourquoi se limiter à une seule valeur ?
• On met 0 dans un compteur qu’on nomme F.
• Pour chaque valeur de X variant de 1 à N on crée une liste de P nombres entiers aléatoires pris entre 0 et 364 et on nomme L1 cette liste.
• On ordonne L1 dans l’ordre croissant et on ajoute à L1 un terme supplémentaire égal à son dernier terme de sorte que les deux derniers termes de L1 soient égaux.
• On met 1 dans un nouveau compteur qu’on nomme B.
• On demande à la machine de « balayer » la liste L1 tant qu’elle ne trouve pas deux termes égaux, le compteur B augmentant de 1 à chaque fois que les deux termes consécutifs rencontrés sont différents.
• On fait le test suivant : si B est différent de P alors le compteur F augmente de 1, car la machine a rencontré deux termes égaux avant P.
• Le travail précédent étant fait pour chacune des N listes L1, on demande à la machine d’afficher le compteur F divisé par N, ce qui est la fréquence des listes L1 qui n’ont pas tous leurs termes distincts.
• L’algorithme est terminé.

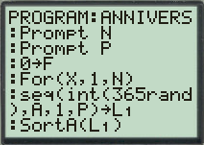
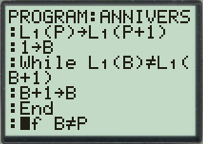
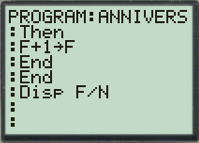
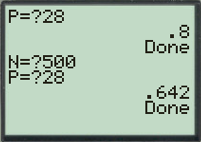
Les écrans suivants donnent le programme, sur TI 83, correspondant à cet algorithme, le dernier écran donnant la fréquence demandée pour N=10, ce qui n’est pas significatif, et pour N=500 :

Calcul de la probabilité

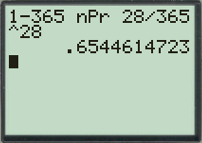
La probabilité cherchée est égale à : $1 - \frac{A^{28}_{365}}{365^{28}}$.
Ce calcul, lourd à effectuer « à la main », est fait par la machine dans l’écran suivant :

Si, au lieu de prendre 28 élèves on en prend 40 les simulations revêtent une importance particulière, car le calcul à effectuer à la machine dépasse ses capacités comme l’indique l’écran suivant :

Le calcul me semble bien trop lourd à effectuer « à la main » !

Autour du minimum d’une fonction

La fonction f définie par $f(x) = \sum_{i=1}^{n} a_i (x-x_i)^2$, où les $x_i$ sont n réels donnés ainsi que les $a_i$ et où l’on suppose de plus que $\sum_{i=1}^{n} a_i > 0$, possède un minimum et ce résultat trouve une application en statistique et une autre dans le chapitre « Barycentre dans le plan et dans l’espace » du programme de 1re S : voilà ce qui constitue l’objet de cette activité.

Ce travail peut aussi être présenté à une classe de TS.

On peut se contenter de travailler avec une valeur de n pour rester au niveau de la classe de 1re S, mais dans ce texte on fait le travail avec $n \in$ N.

1) Montrer que la fonction f possède un minimum et déterminer celui-ci.

La fonction f est dérivable sur R et $f’(x)= \sum_{i=1}^{n} 2a_i (x-x_i)=2 \left (x \sum_{i=1}^{n} a_i - \sum_{i=1}^{n} a_i x_i \right).$

La fonction $f$ admet donc clairement un minimum pour $x= \frac{\sum_{i=1}^{n} a_i x_i}{\sum_{i=1}^{n} a_i}$.

On peut ici explorer le problème avec la TI83, par exemple.

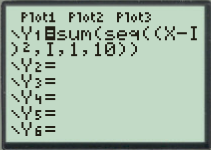
a) On rentre dans l’éditeur de fonction la fonction de l’écran qui suit où on a pris n = 10, $x_i=i$ et $a_i=1$.

La fenêtre d’affichage :

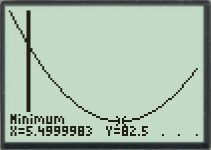
On a demandé le minimum :

Ici il faut interpréter : x = 5.5 et y = 82.5.

Les élèves ne vont pas être sans remarquer que la courbe de f est une parabole : on va donc leur demander de valider cette conjecture.

2) On considère la série statistique qui prend pour valeurs les $x_i$ avec l’effectif $a_i$. Montrer que la fonction g définie par $g(x)= \frac{f(x)}{\sum_{i=1}^{n} a_i}$ admet pour minimum la variance de la série statistique.

3) On considère, par exemple, un tétraèdre ABCD de l’espace muni d’un repère orthonormal : $A(x_A,y_A,z_A)$ ; $B(x_B,y_B,z_B)$ ; $C(x_C,y_C,z_C)$ ; $D(x_D,y_D,z_D)$ ; et quatre réels a, b, c, d tels que $a+b+c+d > 0$. On se pose la question : existe-t-il un point M qui minimise la somme $aMA^2 + bMB^2 + cMC^2 + dMD^2$ ? On sait résoudre ce problème en utilisant le produit scalaire et le barycentre ; cette activité propose une autre démarche.

En posant M(x, y, z), on a :

$aMA^2 +bMB^2 +cMC^2 + dMD^2$

$= a(x-x_A)^2 +b(x-x_B)^2 + c(x-x_C)^2 + d(x-x_D)^2 + a(y-y_A)^2 + b(y-y_B)^2 + c(y-y_C)^2 + d(y-y_D)^2$

$\quad +~: a(z-z_A)^2 + b(z-z_B)^2 + c(z-z_C)^2 + d(z-z_D)^2$

$= f_1(x) + f_2(y) + f_3(z).$

$f_1$, $f_2$, $f_3$ sont des fonctions du type de celle définie dans le préambule, on peut donc leur appliquer 1) :

$f_1$ admet un minimum pour $x_1 = \frac{ax_A+bx_B+cx_C+dx_D}{a+b+c+d}$

$f_2$ admet un minimum pour $y_2 = \frac{ay_A+by_B+cy_C+dy_D}{a+b+c+d}$

$f_3$ admet un minimum pour $z_3 = \frac{az_A+bz_B+cz_C+dz_D}{a+b+c+d}$

On a : $f_1(x_1) + f_2(y_2) + f_3(z_3) \leq f_1(x) + f_2(y) + f_3(z)$ pour tout (x, y, z) $\in$ R$^3$.

En considérant le point G de coordonnées $(x_1,y_2,z_3)$, qui est clairement le barycentre du système pondéré [(A, a), (B, b), (C, c), (D, d)], on a donc : $aGA^2 + bGB^2 + cGC^2 + dGD^2 \leq aMA^2 + bMB^2 + cMC^2 + dMD^2$ pour tout point M de l’espace.

Le point G est donc la solution au problème posé.