La proposition "$\forall n \in \N, n^2+n+41 \mbox{ est premier}$" est fausse. Il est plutôt facile de démontrer qu’elle est fausse, il suffit de montrer un contre-exemple (par exemple avec $n=41$). Mais si on demande à des élèves de démontrer ladite proposition, beaucoup d’entre eux vont essayer pour plusieurs valeurs de $n$ et trouver des nombres premiers :
| n | $n^2+n+41$ | statut |
| 0 | 41 | premier |
| 1 | 43 | premier |
| 2 | 47 | premier |
| 3 | 53 | premier |
| 4 | 61 | premier |
| 5 | 71 | premier |
| 6 | 83 | premier |
| 7 | 97 | premier |
| 8 | 113 | premier |
| 9 | 131 | premier |
| 10 | 151 | premier |
Au bout de quelques lignes, le "on voit bien que $n^2+n+41$ est toujours premier" se transforme insidieusement en "c’est bien la preuve que $n^2+n+41$ est toujours premier". D’ailleurs si on vérifie avec la valeur suivante : $n=11$, $11^2+11+41=173$ est premier ! Et voilà !
Cette façon de faire illustre bien la différence qu’il y a entre induction (logique) (le raisonnement de l’élève) et déduction logique (le raisonnement attendu par le prof). Le fait que la preuve par récurrence ressemble plus à une induction qu’à une déduction, et l’enseignement de plus en plus présent, de la statistique inférentielle, n’arrangent pas les choses...
Mais tout de même, l’élève qui répond "oui d’après le tableau ci-dessus" a-t-il autant faux que celui qui répond "oui parce que $0^2+0+41=41$ qui est premier" ? Avant de répondre que oui, il est bon de se rappeler que la conjecture $\forall n \in \N, 2^{2^n}+1\mbox{ est premier}$ a résisté un siècle (de Fermat à Euler) à des gens que l’on serait enclin à considérer comme plus forts que le lycéen moyen...

Le monkey de CaRMetal permet justement de donner une note de qualité à une construction, sous la forme d’un pourcentage de constructions correctes parmi les variantes obtenues en secouant la figure. Quelques exemples ci-dessous :
Arcanes
Depuis la version 3.5, CaRMetal possède un nouveau bouton qui représente un singe :

(en y regardant bien, on dirait plus particulièrement un macaque rhesus)

Tant que ce bouton est enfoncé (clic gauche de la souris), les points qui ne sont pas fixes ni liés à des courbes parcourent au hasard la fenêtre graphique en suivant une marche aléatoire dont l’angle de rotation n’est pas nécessairement $\frac{\pi}{2}$ mais un angle aléatoire uniforme entre $\pm \frac{1}{2}$ radian (qu’Éric Hakenholz appelle spin), le rayon vecteur étant toujours de 5 pixels (extrait de PointObject.java dans le code source de CaRMetal, lequel est placé sous license GNU GPL) :

Lorsqu’un point, sous l’influence du Monkey, tente de sortir de la fenêtre, il rebondit de manière à retourner vers l’intérieur de celle-ci, en suivant un algorithme qui rappelle les réflexions élastiques de l’algorithme Gendy de Iannis Xenakis (à part qu’ici, le contexte est graphique bidimensionnel, alors que Gendy synthétise des sons stochastiques).
Pour voir l’effet produit sur le mouvement d’un point par le Monkey, il suffit de construire un point et de cocher l’option "activer la trace" de ce point (onglet "aspect" de ses propriétés). On voit alors la trace laissée par le point :
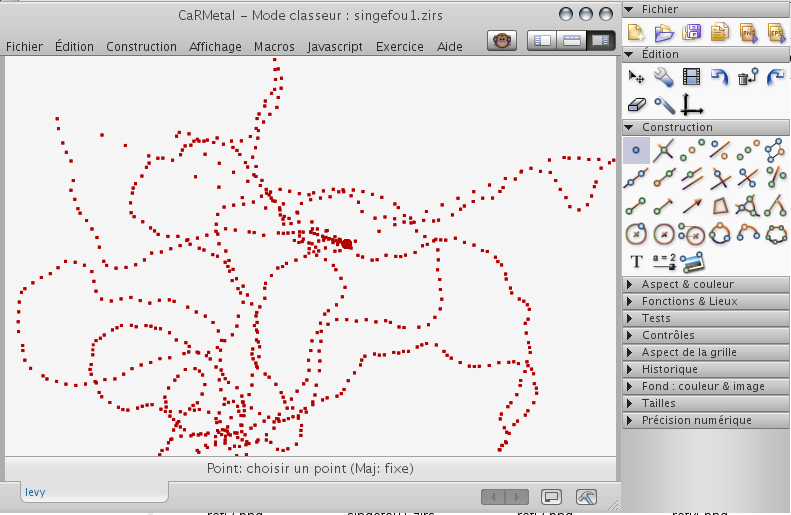
À l’intérieur de la fenêtre, le mouvement du point est une marche aléatoire, approximation d’un mouvement brownien, et la position instantanée du point est un vecteur aléatoire gaussien d’espérance la position initiale du point, et dont l’écart-type est fonction croissante du temps (pour être précis, proportionnel à la racine carrée de celui-ci). De plus, les rebonds sur les bords de la fenêtre sont non linéaires et il est difficile de prévoir le comportement à long terme du Monkey de manière probabiliste. L’expérience montre que le parcours du point est uniforme dans la fenêtre ! Voici comment on peut le vérifier :
On crée un rectangle dont les sommets ont pour coordonnées respectives
(windoww/2,windowh(4))
(windoww/2,-windowh/4)
(-windoww/2,-windowh/4)
(-windoww/2,windowh/4)(qui est donc l’homothétique de la fenêtre entière, avec pour rapport $\frac{1}{2}$) ce qui fait que ce rectangle ne bougera pas puisque en définissant les coordonnées de ses sommets par formules, ceux-ci sont devenus fixes :

et puisque ce rectangle a été baptisé du doux nom de poly3 par CaRMetal, compter le nombre de fois que le point mobile P1 sera à l’intérieur du rectangle, avec
sum(inside(P1,poly3))et diviser par le nombre total de positions du point P1 qui n’est autre que
sum(1)Au bout de quelques minutes, la fréquence de passage dans le rectangle se rapproche de $\frac{1}{4}$ :

Le fait que la fréquence s’approche de $\frac{1}{4}$ alors que le rapport de l’homothétie est $\frac{1}{2}$ est intéressant à analyser en ces temps de disparition du rapport des aires du programme de Seconde...




Commentaires