
La pierre de Mazurkiewicz
Vincent Borrelli, université Claude Bernard Lyon 1
La pierre de Mazurkiewicz, un fabuleux diamant exposé à la Tate Gallery à Londres, vient d’être dérobée au nez et à la barbe des services de sécurité. Devant le désarroi de la police, nous mènerons l’enquête à la manière de Sherlock Holmes, avec pour seules armes les mathématiques et la logique.
Illustration : David Hilbert et Sherlock Holmes, photomontage à partir d’une illustration de Sidney Paget.

Quelle est la forme de l’Univers ?
Vincent Borrelli, université Claude Bernard Lyon 1
En 1820, Carl Friedrich Gauss accompagné de quelques hommes part à l’assaut du mont Brocken. Exploit sportif ? Certainement pas, le mont Brocken est à peine plus haut qu’une colline. Non, il s’agit de bien autre chose : on raconte en effet que Gauss voudrait — ni plus, ni moins — mesurer la courbure de l’Univers...
Illustration : Jeff Weeks, Curved Spaces.

Les Cordées de la réussite
Claudine Boutel et les élèves du lycée Le Verger, Sainte-Marie
Le lycée Le Verger, situé en zone urbaine sensible, est néanmoins animé d’une réelle volonté de mener le maximum d’élèves à poursuivre des études supérieures ambitieuses. Les Cordées de la réussite sont un projet construit autour d’un partenariat entre des établissements d’enseignement supérieur (université de la Réunion, classes préparatoires aux Grandes Écoles) et les entreprises de la région. Dans ce dispositif, les étudiants et les chercheurs ont un rôle majeur à jouer en ayant un lien solide avec des lycéens parfois très craintifs, mais présentant potentiellement des aptitudes à poursuivre des études longues. Il s’agit avant tout de les aider à construire leur parcours de formation et à casser certaines représentations sur les mathématiques.

Quand on a maths et français en même temps
René Cori, université Paris Diderot, ancien président de l’ADIREM
De plus en plus pratiquée, la narration de recherche offre une entrée originale dans les mathématiques. Elle favorise travail en groupe, prise d’initiative de chacun, mise en situation de recherche et expression orale et écrite. Notre équipe la pratique dans des classes de milieu défavorisé, en complète collaboration avec des professeurs de lettres. Langage et raisonnement sont deux éléments cruciaux pour les deux disciplines. Nos interventions communes sur ces thèmes s’avèrent efficaces pour intéresser beaucoup d’élèves, notamment ceux qu’une pédagogie plus classique motive peu.

Math.en.Jeans
Sophie Fur et les élèves du lycée Jean-Hinglo, Le Port
En mettant les jeunes aux prises avec d’authentiques problèmes, le dispositif Math.en.Jeans inverse la tendance courante de la classe de mathématiques et assigne à l’enseignant un rôle différent. Pour se lancer dans l’étude, il n’est plus nécessaire de posséder tous les outils et la démarche de résolution n’est plus détenue par le maître. Certitudes et réponses cèdent la place au doute et au questionnement. Loin d’être réservée à une élite, l’activité s’adresse à tous : c’est par la représentation, la formulation, le débat et la critique que se forgent les connaissances et s’affirment les capacités créatrices. Une classe du lycée Jean-Hinglo, engagée dans ce dispositif, présentera les résultats de ses recherches sur trois thèmes qu’elle a explorés cette année : ensembles infinis, analyse non standard, triplets pythagoriciens.

À la recherche d’invariants
Jérôme Germoni, directeur de l’IREM de Lyon, vice-président de l’ADIREM
Comment savoir d’où est prise la photo ? Même si on repère quelques points qu’on sait placer sur une carte, l’appareil déforme les angles et les distances et on ne sait pas très bien quoi mesurer. Si on veut se convaincre que tel problème de pavage, telle variante d’un
jeu comme le solitaire ou le taquin n’a pas de solution, il n’est pas question d’essayer toutes les solutions : il y en a trop. Comment faire, alors ?
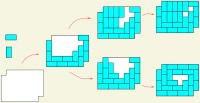
Dans ces deux situations, la clé, c’est de repérer une quantité qui ne varie pas (entre la réalité, la photo et la carte d’une part ; à chaque
étape du jeu d’autre part). On peut alors faire des calculs facilement. Mais cette idée est plus profonde qu’il n’y paraît. On donnera des exemples tirés des mathématiques et d’autres sciences, pour illustrer l’importance de la notion d’invariant, en lien avec les problèmes de
classification et l’idée de symétrie.

Les mathématiques financières et la monétarisation de la société
Stéphane Gombaud, professeur de philosophie au lycée Leconte de Lisle, Saint-Denis
Si la crise économique n’est aujourd’hui pas terminée, il est toutefois possible de porter un regard critique sur les choix qui ont été faits et sur les voies dans lesquelles notre société s’est résolument engagée. La cupidité et le cynisme semblent plus répandus que jamais. De manière étonnante, on découvre alors le rôle déterminant joué par des acteurs de l’ombre, les « quants », les spécialistes des mathématiques appliquées à la finance. Leur intelligence et leur créativité au service de la modélisation des évolutions des cours pourtant chaotiques ou de la mise au point de programmes optimisant les profits seraient pour partie responsable des proportions incroyables prises par la crise financière. Avant de se lancer dans un procès en sorcellerie, il convient toutefois de préciser de quoi on parle. Quel rôle jouent les mathématiques dans cette histoire ? Que font les « quants », à quelle expertise se livrent-ils ? Et il est également nécessaire de mettre en perspective la responsabilité des uns et des autres, des décideurs et des exécutants, des politiques et des brasseurs d’affaires, des escrocs et des honnêtes gens. Les savants, les experts et même les « traders » qui ont été si décriés sont-ils des boucs-émissaires ? L’argent nous a-t-il tous aveuglés ? Le développement prodigieux des mathématiques financières est sans doute très emblématique, ainsi que les problèmes de responsabilité qu’il soulève. Et c’est à une réflexion très générale sur la monétarisation de la société qu’il semble urgent de se livrer.
Illustration : Tangente Hors-Série n° 32, Maths et Finance, Éditions POLE.
2 - 3 = ? Une approche élémentaire des nombres p-adiques
Nicolas Saby, directeur de l’IREM de Montpellier, président de l’ADIREM
Comment les algorithmes des quatre opérations que l’on apprend à l’école élémentaire peuvent amener à la définition de nouveaux nombres ? L’exploration de l’algorithme de la soustraction ou de la division nous amènera à visiter le monde des nombres p-adiques et à résoudre quelques problèmes simples que l’on ne sait pas résoudre dans le monde des entiers ou des réels.
Illustration : Laura Fainsilber.

Pour une réflexion pédagogique de qualité
Xavier Sorbe, inspecteur général de mathématiques
Entre liberté pédagogique de l’enseignant et autonomie des établissements, l’institution se risque de moins en moins à des recommandations pédagogiques. Il ne serait pourtant pas responsable de livrer les enseignants à eux-mêmes sur un certain nombre de thèmes essentiels. Les pratiques d’enseignement conditionnent pour une bonne part la réussite des élèves, il paraît donc indispensable de nourrir efficacement la réflexion pédagogique. Comment favoriser la diffusion de quelques principes avérés ? Comment développer une recherche qui serve les pratiques des acteurs ?
Référence : X. Sorbe, Cinq défis pour l’école. Réflexions et propositions en faveur du système éducatif, L’Harmattan, Paris, 2008.

Évaluer des compétences : pourquoi et... comment ?
Xavier Sorbe, inspecteur général de mathématiques
L’évaluation par compétences est au coeur de nombreuses problématiques. Légitimée par des enjeux politiques majeurs, soutenue par des organismes internationaux, stimulée par les résultats des évaluations internationales, elle se concrétise notamment par l’instauration d’un socle commun.
Quels principes et modalités promouvoir pour une mise en œuvre réussie ?

Le XVIIIe : le siècle des Lumières ou l’âge d’or de l’Addition ? Illustration par la comptabilité de l’élite du négoce et de la banque
René Squarzoni, université de la Réunion
Les mathématiques connaissent un essor impressionnant au cours du XVIIIe siècle, cela rend confondant l’observation de l’archaïsme des représentations numériques et la modestie des instruments arithmétiques au sein de l’élite du négoce et de la banque. Enfermés dans une approche pré-algébrique et englués dans une métrologie archaïque, des opérateurs conduisant des opérations techniquement élaborées et économiquement complexes, ont fondé sur la seule addition toute une comptabilité fiable et valide qui restera en usage durant deux siècles.
Algorithmes et algorithmique
Marie-Catherine Vatonne, université de la Réunion
Un algorithme est une suite d’instructions qui permet d’aboutir à la solution d’un problème. En informatique, l’algorithmique est ce qui se passe avant la programmation. Pour qu’un ordinateur puisse corriger les fautes d’orthographe, proposer un circuit de camion-poubelle, trouver les 1 270 000 pages Internet contenant le mot « algorithme » (en 0,06 secondes !), il a fallu et il faut encore que pas mal d’informaticiens se creusent la tête. Concevoir un algorithme, vérifier qu’une machine est capable de l’exécuter et qu’elle va le faire en moins de 10 000 ans (montre en main) demande des compétences certaines. Cependant, c’est bien moins difficile que cela en a l’air, parce que, depuis tout petit, chacun invente et utilise des algorithmes.
À propos : pourriez-vous m’indiquer où se trouve la salle de conférences, s’il vous plaît ? Je serais bien contente de suivre vos instructions. ;-)

Éclairage cognitif sur la complexité de différents systèmes de numération
Xavier de Viviés, université de la Réunion
La manipulation des nombres passe par le biais d’un système de numération. Il en existe de nombreux mais tous ne sont pas équivalents du point de vue des représentations qu’ils vont induire chez un sujet confronté à la nécessité d’effectuer un calcul. En nous appuyant sur les facteurs cognitifs responsables de la plus ou moins grande complexité des représentations mentales, nous allons présenter un cadre d’analyse systématique des systèmes de numération (Zhang et Norman, 1995). Nous verrons ensuite comment cette taxonomie permet d’éclairer les avantages et les inconvénients des différents systèmes, du point de vue de l’aisance avec laquelle on peut les manipuler pour effectuer des raisonnements mathématiques.
Référence : J. Zhang, D. A. Norman, A representational analysis of numeration systems, Cognition 57 (1995), 271-295.


Commentaires