Listes
Voici un extrait du programme de première (thème algorithmique) :
| Contenus | Capacités attendues | Commentaires |
| Parcours séquentiel d’un tableau | Écrire un algorithme de recherche d’une occurrence sur des valeurs de type quelconque. Écrire un algorithme de recherche d’un extremum, de calcul d’une moyenne. |
On montre que le coût est linéaire. |
En classe de 1re, ces algorithmes sont présentés de façon itérative car cela permet mieux d’aborder des questions purement algorithmiques comme les variants, invariants et le coût. Il a été demandé, en terminale, de refaire le tout en version récursive.
Les énoncés ont été postés sur DocShare, et les copies des élèves ont été récoltées au même endroit. On ne verra donc pas ici les brouillons qui étaient néanmoins instructifs sur les processus d’apprentissage de la récursivité, et plus généralement, de la programmation fonctionnelle.
Longueur
On demandait de programmer récursivement (en Python) une fonction associant, à une liste, sa longueur entière.
Solution astucieuse mais pas récursive :
def longueur(liste):
l = liste
return len(str(l))//2Essai d’utilisation d’une variable locale (donc programmation fonctionnelle impure) :
def longueur(liste):
taille = 1
if liste.suivant == None:
return taille
else:
taille += longueur(liste.suivant)
return taillePassage d’un argument par valeur (probablement inspiré par le cours) :
def longueur(liste,n=0):
n+=1
if liste.est_dernier():
return n
else:
return longueur(liste.suivant,n)Solution pas totalement récursive :
def longueur(liste, total =1):
if not liste.est_dernier():
total += 1
return longueur(liste.suivant, total)
return totalSolution d’un élève exceptionnel :
def longueur(liste):
if not(liste.est_dernier()):
return 1 + longueur(liste.suivant)
return 1Minimum
Ici on demandait de programmer récursivement une fonction associant à une liste de nombres (des entiers) son plus petit élément.
Solution mixte (avec variable) :
def minimum(liste, a) :
if liste is None:
return a
else:
if liste.valeur < a :
a = liste.valeur
return minimum(liste.suivant, a)Solution avec passage d’un argument (ébauche de mémoïsation) :
def minimum(liste,n):
if liste is None:
return n
elif liste.valeur >= n:
return minimum(liste.suivant,n)
else:
n = liste.valeur
return minimum(liste.suivant,n)Solution (brouillon) mélangeant programmations récursive et itérative :
def minimum(liste, pos=0):
l = str(liste)
if liste is None:
return liste.suivant.est_dernier()
if l[pos] == min(l):
return min(l)
pos += 1
return minimum(liste,pos)Solution [2] avec passage d’un argument inutile ici :
def minimum(liste, nb):
if liste is None:
return nb
else:
if liste.valeur < nb:
nb = liste.valeur
return minimum(liste.suivant, nb)Maximum
Cet énoncé, similaire au précédent (il s’agissait de programmer récursivement la fonction qui, à une liste d’entiers, associe son maximum), a été donné plusieurs semaines après, donc à un stade plus avancé de l’apprentissage.
On voit ici (c’est le même élève qui a débuté l’onglet précédent) un net progrès dans la conceptualisation non seulement de la récursivité, mais aussi dans le paradigme fonctionnel :
def maximum(liste):
if liste is None:
return float('-inf')
else:
return max(liste.valeur,maximum(liste.suivant))Solution presque haskellienne :
def maximum(liste):
if liste is None:
return -float('inf')
else:
return max(liste.valeur, maximum(liste.suivant))Il ne faudrait pas croire pour autant que tous les élèves de terminale maîtrisent la récursivité à la fin du premier trimestre :
def maximum(liste):
...Solution d’un élève n’ayant pas choisi le tandem NSI+maths :
def maximum(liste):
if liste is None:
return float('-inf')
return max(liste.valeur, maximum(liste.suivant))Solution de l’élève qualifié d’exceptionnel (maths+NSI) :
def maximum(liste):
if liste is None:
return float('-inf')
return max(liste.valeur, maximum(liste.suivant))Somme
On demandait de programmer récursivement la fonction qui, à une liste d’entiers, associe la somme de ces entiers.
Solution itérative (donc ne respectant pas le contrat) :
def somme(liste):
S = 0
if liste == []:
return 0
else:
for i in range(len(liste)):
S = S + L[i]
return SSolution avec variable intermédiaire :
def somme(liste, s=0):
if liste == None :
return s
else:
s += liste.valeur
return s + somme(liste.suivant)Solution élégante (maths+NSI) :
def somme(liste):
if liste is None:
return 0
else:
return liste.valeur + somme(liste.suivant)Corrigé
Voici les attendus
On ne le voit pas sur les propositions (parfois) terminées, mais il y a en cours d’apprentissage une certaine tendance à confondre print et return et plus généralement, à mélanger des éléments de programmation itérative (avec laquelle les élèves semblent se sentir plus à l’aise en début de terminale) et de programmation récursive. On peut y voir le phénomène classique de recherche de confort avec ce qu’on connaît et comprend mieux.
Une remédiation proposée est de ne jamais utiliser print en Python, ce, dès la classe de 2nde, et ce, dans toutes les matières. Voir aussi cet article assez critique sur le sujet.
Le copier-coller aussi peut être un bon moyen de résoudre un problème, mais il faut trouver quoi copier avant de coller : traduire un algorithme itératif en version récursive, s’est révélé à l’usage moins efficace que simplifier les algorithmes sur les arbres binaires :
- une liste est un cas particulier d’arbre binaire
- la longueur d’une liste est un cas particulier de taille d’un arbre binaire.
Du coup il suffisait de transformer
def taille(arbre):
if arbre is None:
return 0
else:
return 1+taille(arbre.G)+taille(arbre.D)en
def longueur(liste):
if liste is None:
return 0
else:
return 1+longueur(liste.suivant)ce qui est un simple renommage.
Par ailleurs, la programmation récursive est essentiellement affaire de définition, et programmer récursivement revient souvent à se poser des questions comme « qu’est-ce que c’est ? » ou « de quoi parle-t-on ? ». Ce fut particulièrement flagrant lorsqu’il a fallu gérer les cas d’arrêt comme
- Quelle est la longueur d’une liste vide ?
- Quelle est la somme des éléments d’une liste vide ?
- Quel est le minimum d’une liste vide ?
- Quel est le maximum d’une liste vide ?
Ces deux dernières questions semblent d’un niveau mathématique élevé par rapport à la classe de terminale...
Block2Pyf
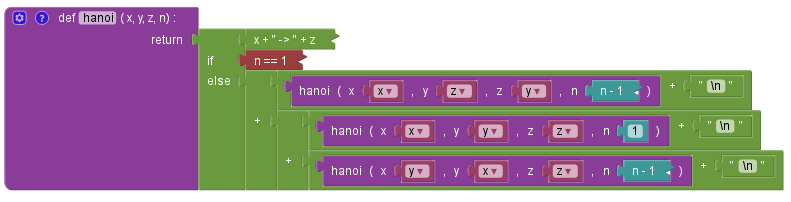
La version fonctionnelle de Block2Py permet de programmer récursivement par blocs, grâce à l’opérateur ternaire qui permet de considérer les branchements conditionnels comme des expressions.
Block2Pyf ne gérant pas les listes, on transporte les algorithmes dans le champ des chaînes de caractères.
Les copies d’écran ci-dessous sont cliquables et permettent de télécharger le fichier au format Block2Py.
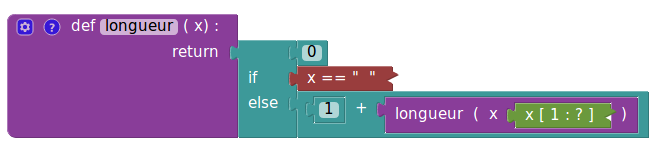
Longueur
Ici le cas de base est le mot vide :
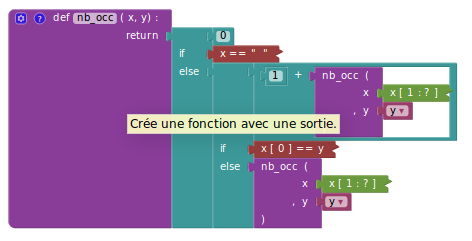
Appartenance
Minimum
L’algorithme n’a de sens que s’il existe une relation d’ordre entre les éléments de la liste. Ici c’est l’ordre alphabétique, en supposant que les majuscules viennent avant les minuscules (ordre sur les entrées unicode des caractères).
On convient que la lettre minimale du mot vide est une lettre supérieure à toutes les lettres possibles dans le mot. Ici on a choisi la lettre « » :
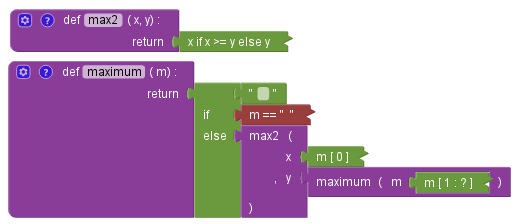
Maximum
On convient que la lettre maximale du mot vide est une lettre inférieure à toutes les lettres présentes dans des mots non vides. Ici on a choisi le caractère espace, dont le code Ascii est 32 (alors que les codes Ascii des lettres de l’alphabet latin valent tous au minimum 65) :
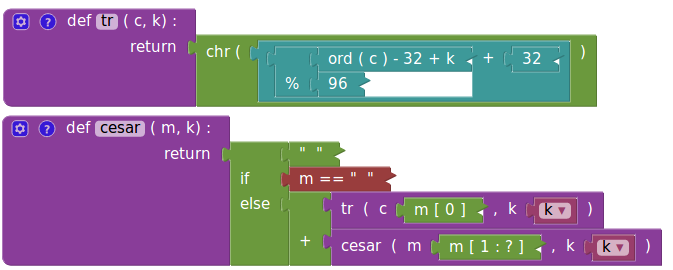
Somme
Pour que cet algorithme ait un sens, il faut qu’il existe une addition entre les éléments de la liste. Pour des caractères c’est le cas : la concaténation. Mais alors la somme de toutes les lettres d’un mot est le mot lui-même, ce qui n’est pas spécialement intéressant. Alors on se propose de programmer la fonction qui, à un mot, associe la somme des codes Ascii de ses lettres :
Fonctions
Une difficulté qui apparaît lorsqu’on essaye de sensibiliser les élèves à la notion de récursivité, est que pour cela on gagne à parler fonctionnel, et c’est une autre notion difficile et abstraite à appréhender en plus de la récursivité. Typiquement l’écriture d’une fonction récursive ressemble à
def fonction(args):
if cas_de_base():
return quelque_chose_de_simple
else:
return une_expression(fonction(autres_args))Or si, en terminale, la plupart des élèves sont à l’aise avec la syntaxe if...else, certains ont du mal à distinguer print et return. C’est là que ça bloque apparemment [3].
Un exercice donné en première montre cette difficulté et son évolution.
Énoncé
On demandait de compléter la fonction maximum pour qu’elle renvoie le plus grand nombre d’un tableau, en s’inspirant de la fonction minimum du cours (rappelée ci-dessous) :
L = [1,2,13,5,4,3,8,16]
def longueur(tableau):
compteur = 0
for x in tableau:
compteur += 1
return compteur
def est_dedans(elt,tableau):
for x in tableau:
if elt==x:
return True
return False
def minimum(tableau):
entier = float('inf')
for elt in tableau:
if elt <= entier:
entier = elt
return entier
def maximum(tableau):
....
return ...Réponses
Voici la réponse proposée par un élève :
L = [1,2,13,5,4,3,8,16]
def maximum(liste):
maxi = liste[0]
longueur = (len(liste))
for n in range(longueur):
if liste [n] >= maxi:
maxi = liste[n]
return maxi
print(maximum(L))C’est un élève qui a compris, ou bien la programmation fonctionnelle, ou alors comment on peut copier-coller depuis le cours (ou toute autre ressource sur le web). Mais c’est quand même un élève qui pratique la programmation fonctionnelle.
Un élève montre qu’il a compris le fonctionnement de l’algorithme mais pas celui des fonctions :
L= [1,2,13,5,4,3,8,16]
maxi=0
for i in L:
if i >= maxi:
maxi = i
print(maxi)Cette autre réponse témoigne d’une autre incompréhension, celle de l’énoncé :
def max_liste(liste):
a=max(liste)
return aUn autre élève a créé une autre fonction que celle qui était demandée :
def pas_dedans (elt,tableau):
for x not in tableau :
else x**elt:
return FalseSomme
On demandait une fonction qui, à un tableau de nombres, associe la somme de ces nombres. L’attendu était quelque chose comme ceci :
def total(tableau):
somme = 0
for elt in tableau:
somme += elt
return sommeCette solution est presque bonne :
def sommeIndices(tableau,debut,fin):
somme = 0
for i in range(debut,fin+1):
somme = somme + tableau[n]
return sommeCette solution est typique car elle montre la confusion entre print et return :
def total(tableau):
return tableau
s = 0
for x in L:
s += total(x)
print(s)Cette solution montre la difficulté qu’il y a à initialiser une variable :
def somme(liste):
somme = 1
for i in liste:
somme = somme + i
return sommeCelle-là montre la difficulté qu’il y a à saisir la syntaxe des fonctions :
def somme(listefdebutfin)
for i in range(début+fin+1):
somme = somme + liste[i]
return sommeCelle-là aussi :
def totale(x)
return x
y = 0
for z in L:
y += totale(x)
print yCette solution correcte montre le goût des élèves pour les opérations in situ :
def somme(liste):
total = 0
for nombre in liste:
total += nombre
return totalCelle-là semble témoigner de difficultés de compréhension de l’énoncé :
def fonction_total (elt tableau):
if x in tableau :
return True
if x not in tableau :
return False Moyenne
Après la somme, il fallait écrire une fonction Python donnant la moyenne. Là aussi on voit une sorte d’hésitation entre programme et fonction.
def sommeIndices(tableau,debut,fin):
somme = 0
for i in range(debut,fin+1):
somme = somme + tableau[n]
return somme
def moyenne(tableau)
moyenne = somme/effectif
for i in range(début,fin+1)
effectif = somme/longueur(tableau)
return effectifL’élève ne sait pas encore si somme est une variable numérique ou une fonction.
Excellente proposition d’un élève non matheux :
def total(L):
somme = 0
for x in L:
somme += x
return somme
def moyenne(L):
return total(L)/len(L)Proposition du meilleur élève en guise de corrigé :
def moyenne(liste):
somme = 0
for addition in liste:
somme += addition
moyenne = somme / len(liste)
return moyenneLà aussi l’apprentissage de la programmation fonctionnelle est déjà bien avancé :
def somme(liste):
somme = 0
for i in liste:
somme = somme + i
return somme
def moyenne(liste):
return somme(liste)/len(liste)Confusion générale dûe à un excès de copier-coller apparemment :
def moyenne(list):
moyenne = list
resultats = []
for ligne in moyenne:
resultats.append(float)
hist(resultats)
show()
def moyennePartielle(liste,debut,fin):
_somme = sommePartielle(liste,debut,fin)
effectif = fin+1-debut
return _somme(liste)/effectif
def moyenne(liste):
return somme(liste)/len(liste)On constate l’absence d’indentation et la confusion entre print et return :
def totale(x)
return x
y = 0
for z in L:
y += totale(x)
print yAbsence de fonction, et addition entre objets de types différents :
liste = [4,5,4]
total=0
for nombre in range (0,len(liste)):
total = total + liste + nombre
print(total)
print(total/len(liste))Pire
Par la suite, toujours en 1re, a été donné un exercice où il fallait définir une fonction (pour le problème de rendu de monnaie). Et plusieurs élèves ont commencé par
def rendu(monnaie):
monnaie = input("quelle somme de monnaie ?")qui témoigne, là encore, d’une difficulté à concevoir la notion de fonction.
En Seconde
En SNT, un projet a porté sur le texte de Neper sur son abaque binaire. Le principe est qu’à chaque case de l’abaque est associée une valeur et que Neper sait comment sont liées les valeurs des voisines d’une case :
| ... | ... | ... | ... | ... |
| ... | 4x | 2x | x | ... |
| ... | 2x | x | x/2 | ... |
| ... | x | x/2 | x/4 | ... |
| ... | ... | ... | ... | ... |
La théorie de Neper peut être interprétée comme une définition d’une fonction valeur(colonne, ligne) et les axiomes de Neper sont une définition récursive de cette fonction.
Neper
Voici la théorie de Neper (annexe de rhabdologiae) concernant cet abaque :
- Axiome 1 : La valeur de chaque case est le double de la valeur de sa voisine du dessous (si elle en a une) et le double de la valeur de sa voisine de droite (si elle en a une).
- Axiome 2 :
- la valeur d’une case de la marge de droite (colonne = 0) est 2ligne
- la valeur d’une case de la marge du bas (ligne = 0) est 2colonne.
L’axiome 2 est le cas de base de la récursion (on peut aussi parler de suite récurrente et l’axiome 2 démarre la récurrence). L’axiome 1 est celui qui utilise la récursivité puisque le mot valeur y figure non seulement comme sujet de la phrase, mais aussi comme complément.
Neper prouve (mais pas par écrit) les corollaires suivants, à partir de ces axiomes :
- Corollaire 1 : Un mouvement vers le Nord-Est ou vers le Sud-Ouest ne modifie pas la valeur d’une case.
- Corollaire 2 : Un mouvement vers le Nord-Ouest quadruple la valeur d’une case, un mouvement vers le Sud-Ouest la divise par 4.
- Corollaire 3 : Les valeurs des cases situées sur la diagonale principale (numéros de ligne et de colonne égaux) sont les puissances de 4.
- Corollaire 4 : Les valeurs des cases situées juste au-dessus de la diagonale principale sont les doubles des puissances de 4.
- Corollaire 5 : Les valeurs des cases situées juste au-dessous de la diagonale principale sont aussi les doubles des puissances de 4.
- Corollaire 6 : Les valeurs des cases situées deux cases au-dessus de la diagonale principale sont les puissances de 4 en commençant par 4.
- Corollaire 7 : La valeur de toute case est le produit des valeurs des marges : 2colonne.2ligne.
latin
Le texte de Neper est parfaitement lisible pour qui est latiniste :
Pour qui n’est pas latiniste, voici une tentative de traduction de ce texte :
ainsi que le source d’icelle, en LaTeX :
On remarquera en passant que Neper décrit deux pièces de jeu d’échecs qui ne sont plus utilisées aujourd’hui :
- L’éléphant porteur de tour de Neper correspond au Wazir du jeu d’échecs. Solomon Golomb l’appelait duke (intersection du roi et de la tour rook) et il correspond au général de certaines variantes du shogi.
- Le porteur de tour ou vizir correspond au ferz (vizir) du jeu d’échecs. C’est l’ancêtre de la dame et on le trouve notamment dans le jeu alquerkonane.
Voici deux gnomons (c’est comme ça que Neper les appelait) :
Le carré de 7 :

Le carré de 11 :

Petri
L’abaque de Neper, grâce à l’axiome 1 de Neper, peut être considéré comme un réseau de Petri :
En voici le mode d’emploi :
On peut s’entraîner aux groupements-échanges avec ces jeux de semaille sur une marge de l’abaque de Neper :
| vers le binaire | depuis le binaire |
Voici par exemple comment on peut obtenir l’écriture binaire de 5 :
On commence par placer 5 graines (« calculi ») dans la case de valeur 1 (tout à droite : 5×1=5) :

On utilise l’axiome 1 de Neper pour remplacer deux graines de valeur 1 par une graine de valeur 2 (1×2+3×1=5) :

Puis on recommence (2×2+1=5) :

Enfin on remplace 2 graines de valeur 2 par une graine de valeur 4 :

L’algorithme termine toujours (le nombre total de graines est un variant : 5 puis 4 puis 3 puis 2) et donne la représentation binaire du nombre de départ, parce que la condition d’arrêt est qu’aucune case ne contient plus d’une graine.
L’axiome 1 peut servir de preuve pour les deux premiers corollaires :
- Corollaire 1 : un mouvement vers le nord-est est composé d’un mouvement vers le nord (qui double la valeur de la case) et d’un mouvement vers l’est (qui divise la valeur par 2). Les deux mouvements ont des effets contraires et se neutralisent mutuellement. Idem pour un mouvement vers le sud-ouest, qui est composé d’un mouvement vers le sud (diviseur par 2) et d’un mouvement vers l’ouest (doubleur).
- Corollaire 2 : un mouvement vers le nord-ouest est composé de deux mouvements qui doublent la valeur de la case (l’un vers le haut, l’autre vers la gauche). Leur effet combiné est de quadrupler la valeur de la case.
Why
Les corollaires 3 à 7 peuvent se démontrer par récurrence à l’aide du corollaire 2 :
- Corollaire 3 : d’après l’axiome 2, la valeur de la case en bas à droite est 1=40. Et si la valeur en (x,x) est 4x alors celle en (x+1,x+1) est 4×4x=4x+1 d’après le corollaire 2.
- Corollaire 4 : d’après l’axiome 2, la valeur de la case juste au-dessus de celle en bas à droite, est 2=2×40. Et si la valeur de la case (x,x+1) est 2×4x alors d’après le corollaire 2, celle de la case (x+1,x+2) est 4×2×4x=2×4×4x=2×4x+1.
- Corollaire 5 : comme le corollaire 4, ou en appliquant le corollaire 1 au corollaire 4 : pour aller d’une case juste au-dessous de la diagonale, à une case juste au-dessus, on effectue un mouvement vers le nord-est et d’après le corollaire 1, la valeur en (x+1,x) est la même qu’en (x,x+1) soit 2×4x.
- Corollaire 6 : comme le corollaire 4.
- Corollaire 7 : par récurrence sur le numéro de colonne :
- si le numéro de colonne x est égal à 0, d’après l’axiome 2, la valeur de la case est 2y=20×2y (en appelant y le numéro de ligne)
- si la valeur de la case (x,y) est 2x×2y alors, comme la case (x+1,y) est la voisine de gauche de la case (x,y), sa valeur est le double 2×2x×2y=2x+1×2y.
Le problème qui se pose en Seconde est que le raisonnement par récurrence n’y est pas au programme. Pour prouver le corollaire 7 sans faire appel à la récurrence, on peut utiliser le fait que les graduations sur les axes de coordonnées sont logarithmiques mais le logarithme (qui était connu de Neper puisque celui-ci en est l’inventeur) ne sont pas non plus au programme de Seconde. Il a donc été décidé de faire admettre le corollaire 7 et d’en déduire (sans récurrence) les autres.
On peut tester en ligne ce script :
module Neper
use int.Int
use int.Power
let rec function valeur (colonne ligne: int) : int
requires { colonne >= 0 }
requires { ligne >= 0 }
ensures { result = power 2 colonne * power 2 ligne }
variant { colonne }
= if colonne = 0 then power 2 ligne
else if ligne = 0 then power 2 colonne
else 2 * valeur (colonne - 1) ligne
endIl prouve (en fait, certifie) le corollaire 7 (ligne 11). Il est donc possible à partir de celui-ci de prouver les autres sans passer par un raisonnement par récurrence.
Alt-Ergo
On peut également demander à Alt-Ergo de prouver les deux premiers corollaires, avec ce script :
logic valeur: int,int -> int
axiom Axiome2:
valeur(0,0) = 1
axiom Axiome1a:
forall ligne,colonne: int. valeur(ligne+1,colonne) = 2 * valeur(ligne,colonne)
axiom Axiome1b:
forall ligne,colonne: int. valeur(ligne,colonne+1) = 2 * valeur(ligne,colonne)
goal corollaire1: forall x,y: int. x>0 -> valeur(x,y) = valeur(x-1,y+1)
goal corollaire1bis: forall x,y: int. y>0 -> valeur(x,y) = valeur(x+1,y-1)
goal corollaire2: forall x,y: int. valeur(x+1,y+1) = 4 * valeur(x,y)
goal corollaire2bis: forall x,y: int. x>0 -> y>0 -> valeur(x-1,y-1) = valeur(x,y) / 4La réponse indique le nombre d’étapes pour chaque preuve :
# [answer] Valid (0.0630 seconds) (4 steps)
# [answer] Valid (0.0800 seconds) (4 steps)
# [answer] Valid (0.0950 seconds) (3 steps)
# [answer] Valid (0.1850 seconds) (9 steps)On sait aussi combien de fois chaque axiome a été utilisé, en cliquant sur le bouton
Axiome1a lines 5-6 21 inst.
Axiome1b lines 7-8 21 inst.Sympy
La preuve des corollaires 1 à 4 à l’aide du corollaire 7 (considéré comme un axiome, admis car prouvé par why3) fait appel au calcul formel :
- Corollaire 1 : 2x-1×2y+1=2x×2-1×2y×21=2x/2×2y×2=2x×2y/2×2=2x×2y
- Corollaire 2 : 2x×2x=4x
- Corollaire 3 : 2x×2x+1=2x×2x×21=4x×2
- Corollaire 3 : 2x+1×2x=2x×2×2y=2×4x
En voici les preuves par Sympy :

Le corollaire 7 peut servir aussi à prouver que l’algorithme de multiplication de Neper est correct : en écrivant x=Σxi×2i et y=Σyj×2j alors en développant le produit on a x×y=Σxi×yj×2i+j=Σxk×yk-j×2k. Comme les xi et yj sont égaux à 0 ou 1, leur produit n’est égal à 1 que lorsqu’ils sont tous les deux égaux à 1, ce qui se représente par un jeton à l’intersection de la colonne i et de la ligne j chaque fois que xi et yj valent 1.
Conjectures
Dans un premier temps, il a été donné comme devoir, l’abaque à remplir en indiquant dans chaque case, sa valeur, calculée à l’aide des axiomes de Neper. L’idée était de faire découvrir la propagation des calculs lorsqu’on a une fonction récursive : comme dans la programmation dynamique, on commence par calculer les valeurs les plus simples, puis progressivement les valeurs voisines.
Voici un exemple de devoir réussi :
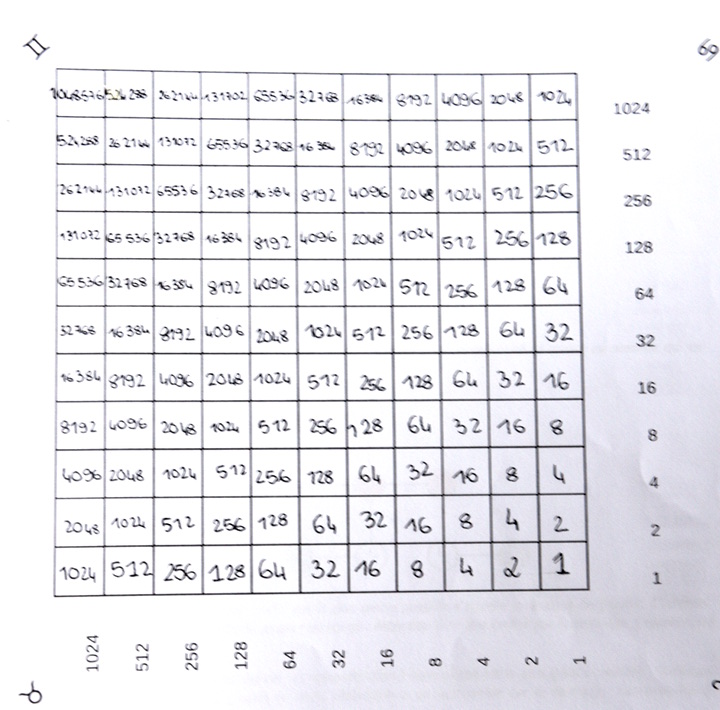
On constate que le devoir a été rendu sur feuille, ce qui mobilise le canal kinesthésique (et c’est tant mieux). Pratiquement tous les devoirs ont été réussis et relativement vite. En effet, en faisant le devoir, des conjectures sont émises puis utilisées pour accélérer le travail. Par exemple le corollaire 1 a été conjecturé au feutre sur ce devoir :
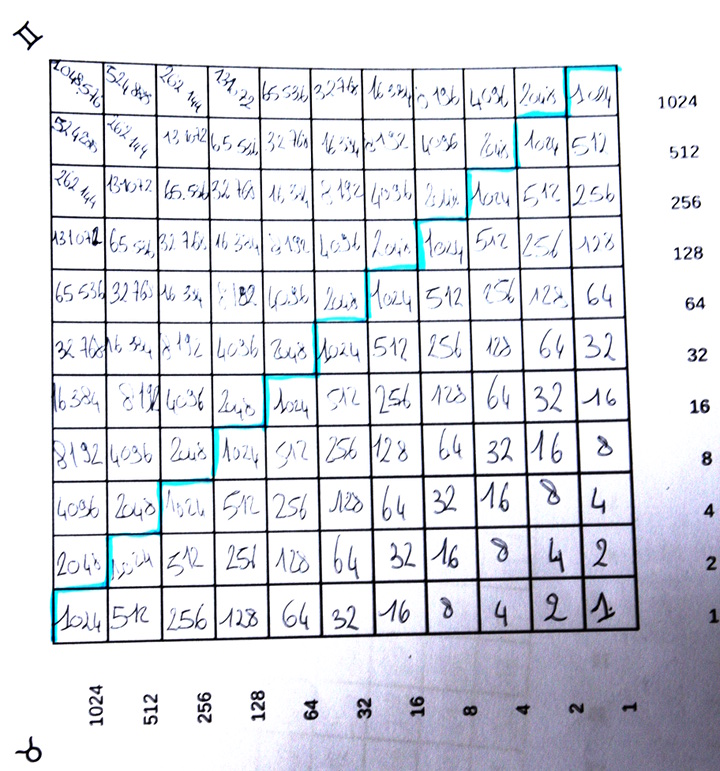
Parmi les 30 élèves ayant rendu le devoir,
| conjecture | émise par | utilisée par |
| axiome 2 (les puissances de 2 dans la marge) | 13 élèves | 8 élèves |
| corollaire 1 | 20 élèves | 15 élèves |
| corollaire 2 (quadruples) | 5 élèves | personne |
| corollaire 3 (puissances de 4) | personne | personne |
| corollaire 5 (symétrie par rapport à la diagonale principale) | 8 élèves | 6 élèves |
| corollaire 7 | 2 élèves | 3 élèves |
On constate qu’une élève a utilisé le corollaire 7 sans l’avoir conjecturé ! L’émission d’une conjecture est une forme de verbalisation, et certains élèves ont fait le devoir tellement vite qu’ils n’ont pas eu le temps de verbaliser.
Personne n’a conjecturé le fait que la case au sud-est vaut le quart mais cela a parfois été déduit du fait que la case au nord-est vaut le quadruple.
Voici une illustration du corollaire 3 :

L’axiome 2 a été conjecturé parce que dans le devoir il n’a pas été donné tel quel, il a été remplacé par la seule valeur en bas à droite qui est 1. Il fallait donc entrer les puissances de 2 dans les marges à la main. Le lien entre
- le fait de doubler à chaque étape, et les puissances de 2
- le fait de quadrupler à chaque étape, et les puissances de 4
semble aller de soi et les élèves ne devraient pas avoir trop de difficulté à aborder les suites géométriques quand ils seront en 1re. Du moins l’espère-t-on.
Preuves
Après les émissions de conjectures, un autre devoir a été donné, consistant à prouver les corollaires 1 à 4 à l’aide du corollaire 7, dès lors considéré comme un axiome :
Une élève a cherché le mot corollaire :

L’erreur de signe sur cette copie est fréquente, il s’agit là probablement d’une erreur de recopie :

Ce devoir est plus étonnant : le mécanisme de preuve est correct mais il est appliqué à un cas particulier :
On voit aussi, en bas de la page, une confusion entre addition et multiplication. Dans d’autres devoirs il y a eu confusion entre 2x et 2x. Ce qui peut expliquer les erreurs vues en terminale, comme la confusion entre 2x et x² : 2x=2x=x×2=x²...
Voici le seul devoir répondant totalement aux attendus :
Mais une bonne surprise sera décrite à l’onglet suivant.
Programmes de calcul
Voici une preuve du corollaire 4 qui n’utilise pas le corollaire 7, mais le corollaire 3 :

En effet,
- d’après le corollaire 3, les nombres sur la diagonale sont les puissances de 4
- d’après l’axiome 1, les nombres juste au-dessus de la diagonale sont les doubles des nombres diagonaux.
Donc les nombres juste au-dessus de la diagonale sont les doubles des puissances de 4 cqfd
Sur la même copie on voit des démonstrations des corollaires 1 et 2 par des graphes :
| corollaire 1 | corollaire 2 |

|

|
Ceci suggère une autre approche, historiquement plus vraisembable (Neper ne connaissait peut-être pas le raisonnement par récurrence et ne disposait certainement pas de why3 ni d’Alt-Ergo !
Les deux approches peuvent être combinées avec Sofus.
En effet, les élèves de 2nde sont (théoriquement) familiarisés avec les programmes de calcul et les preuves de certaines propriétés les concernant.
Par exemple en choisissant un nombre (ici 8), en le doublant puis en le divisant par 2 il n’est pas surprenant que l’on retombe sur le nombre de départ (ici 8 à nouveau) :
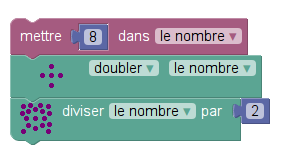
Sofus permet de refaire l’expérience en calcul formel, en appelant par exemple x le nombre de départ :
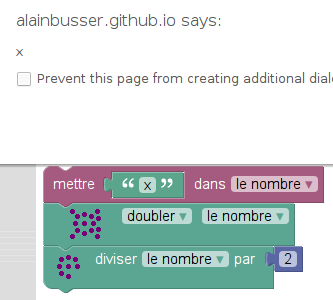
On peut même vérifier (formellement) que l’ordre dans lequel on effectue ces opérations, ne change pas le résultat :

que si on effectue deux fois la division par 2, on obtient le quart du nombre de départ :

et qu’à l’inverse 2 doublements successifs équivalent à un quadruplement :

Comment combiner cela avec la théorie de Neper, qui évoque des déplacements ? On peut tout simplement programmer les fonctions de Neper en codant les déplacements par des flèches.
Pour les mouvements de l’éléphant porteur de tour :

On en déduit les fonctions du vizir :
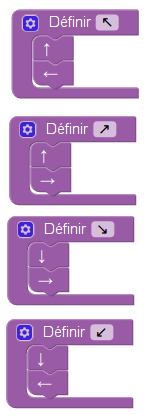
Ce qui permet de montrer (toujours formellement) les deux premiers corollaires de Neper :
- Corollaire 1 :

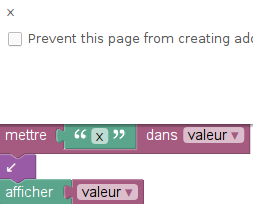
- Corollaire 2 :
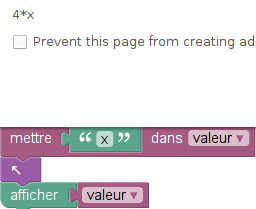
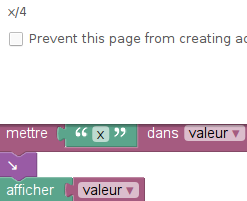
On peut refaire les expériences sur Sofus avec ce fichier :
Prouver le corollaire 3 sans utiliser ni le raisonnement par récurrence, ni le corollaire 7, est plus difficile en 2nde. Par contre, les nombres sur la diagonale sont définis comme une suite géométrique de raison 4, d’après le corollaire 3. Le programme de 1re donne la forme explicite d’une suite géométrique, dans le cas présent 4n. De toute manière le corollaire 3 n’est pas utilisé dans l’algorithme de multiplication.
On a vu comment le corollaire 4 peut être déduit du corollaire 3, et le corollaire 5 peut être démontré de façon similaire ou par symétrie par rapport à la première diagonale. Le corollaire 6 en est une généralisation.
En fait, le corollaire 7 peut être déduit des corollaires précédents sans faire appel à la récurrence : d’après le corollaire 1, la case (x,y) a la même valeur que la case (x+y,0) (trouvée par déplacements vers le sud-ouest jusqu’à la première ligne). Or d’après l’axiome 2, cette case vaut 2x+y=2x×2y cqfd
Résumé :
Cet article part d’un constat : alors que la programmation objet ne pose pas de difficulté conceptuelle majeure à des élèves parfois très jeunes (voir Papert à ce sujet), il en est tout autrement pour la programmation fonctionnelle et la récursivité. Une théorie est émise : le blocage pourrait venir d’une confusion assez fréquente, entre print et return. Cette confusion est peut-être elle-même la conséquence de ce qu’en Python, print est une fonction et return une instruction. Deux remédiations sont proposées :
- ne jamais utiliser print en Python (tout faire avec des fonctions)
- au contraire, aborder les deux pour apprendre dès le début la différence entre eux.
Au lecteur de faire son choix...
Références :
- Voir cet article de Repères IREM
- Seymour Papert : le jaillissement de l’esprit
- Benoît Mandelbrot : géométrie fractale de la nature
- Claude Livercy : théorie des programmes
- programme de NSI Terminale








Commentaires