• Niveau(x) concerné(s) : Cycle 2 - Cycle 3 - Cycle 4 - Lycée
• Temporalité : À tous moments, en classe ou hors murs, lors de manifestations (Semaine des mathématiques, fête de la science)...
• Logiciels/Matériels utilisés : Des cordes, des craies, des galets, des planches à clous… Smartphone et/ou tablettes pour Scratch
• Prérequis : À définir selon les activités
• Objectifs généraux : Développer la pensée algorithmique des élèves et prendre plaisir à faire des mathématiques.
• Connaissances et compétences travaillées : Suivant les ateliers proposés, nous balayons l’ensemble des domaines du S4C ainsi que les six compétences travaillées en Mathématiques.

Nous avons créé des visuels, afin que les élèves puissent identifier et s’approprier le socle commun. Nous avons aussi précisé les éléments signifiants du Cycle 4 de chaque domaine pour faciliter la communication avec les collègues encadrants et la mise en oeuvre d’une évaluation commune.

Modalités de mise en œuvre pédagogique du projet

Des ateliers à ciel ouvert pour favoriser l’approche kinesthésique et la verbalisation de l’algorithmique

On va dehors ! Nous avons souhaité tester le concept de classe “hors murs” à l’intérieur de l’établissement. L’accroche fut motivante pour les élèves. Outils mis à disposition de chaque groupe :

• une corde
• un rapporteur
• des craies de couleurs
• une feuille regroupant les consignes
• des affiches A0 pour toute la classe

Que ce soit au collège, à la Fête de la science ou lors de la Semaine des Mathématiques, La présentation générale des problèmes restait la même : les mathématiques doivent être perçues avant tout comme un jeu et il fallait surtout chercher à prendre du plaisir dans la recherche des réponses aux situations proposées. Chaque groupe avait une demi-heure pour agir. Nous avons pu tester en grandeur réelle les mêmes ateliers avec des participants du cycle 2 au Lycée.
Bien sûr, nous avons dû sensiblement changer notre approche pour adapter la consigne en fonction des aptitudes de nos interlocuteurs.

Des problèmes intercycle : de la verbalisation à Python
D’une manière générale, c’est le travail collaboratif qui fait progresser les élèves, le conflit socio-cognitif est omniprésent et poussent les élèves à la verbalisation. A chaque itération, le vocabulaire se précise et les termes techniques prennent sens dans la représentation conceptuelle des élèves : variable, affectation, boucle, condition et fonction deviennent des mots pragmatiques.

L’interdisciplinarité favorisée
Les ateliers proposés peuvent être mis en connexion avec les Arts Plastiques (Atelier triangle de Sierpinski & Le nombre d’or), le monde agricole (Atelier le verger des nombres), l’Histoire (Atelier Zistoir Marrons), histoires des Sciences (Atelier Formule de Pick), SVT (Atelier Le nombre d’or), les Sciences Sociales (Q-Sort). Pour nos premières expérimentations exposées ici, les professeurs encadrants étaient principalement des professeurs de mathématiques (animateurs IREM).

Analyse a priori

Formule de Pick
#variable #registre #affectation #calcul_litteral

le théorème de Pick fournit une formule simple pour calculer l’aire A de ce polygone en se servant du nombre i de points intérieurs du polygone et du nombre c de points sur le contour du polygone :

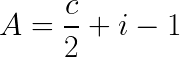
À l’aide d’une planche à clous et quelques élastiques on représente des polygones et on en détermine l’aire

Au Cycle 2 & 3 : découvrir les variables
Nous avons poussé l’activité au bout avec des élèves de CE2 : création des registres “i” et “c”, affectation de valeurs aux variables et verbalisation de l’algorithme. Du calcul littéral au cycle 2 !

Dans un premier temps, il est utile de rappeler aux élèves qu’il faut distinguer le dénombrement de clous et de carreaux. Réaliser un rectangle de 4 carreaux de long et de trois carreaux de large n’est pas la même chose qu’un rectangle de 4 clous de longs et 3 clous de large. C’est un moyen concret de distinguer longueur et aire. La formule de pick nécessite de compter des clous, mais elle donne un résultat en carreaux.

Au Cycle 4 : comprendre les affectations et donner du sens au calcul littéral.
Cette activité nous permet d’aborder le calcul littéral et d’en avoir une application concrète à travers la notion d’affectation de variables. La création d’un programme Scratch est tout à fait indiquée.

Au collège, le vocabulaire des polygones peut-être revisité. Nous pouvons demander aux élèves de construire avec des élastiques des figures symétriques, des agrandissement ou des réductions. Insister sur la différence entre aire et périmètre, deux notions encore trop floues pour nos élèves. L’approche kinesthésique est essentielle et donc nécessaire pour aborder les notions liées à l’algorithmique et la programmation.

Prolongement : Les pixels de Pick
Avec celui de Minkowski, nous avons deux célèbres théorèmes pour compter les points à coordonnées entières dans des convexes ou des polygones. Dans l’univers du numérique en générale du pixel en particulier, les applications sont nombreuses [1]. Par ailleurs, la démonstration du Théorème de Pick est accessible à des élèves scientifiques de Lycée.

Apport du numérique : une planche à clous ! [2]

La main calculette
#retrancher #ajouter #produit_de #programme_de_calcul #calcul_littéral #double_distributivité

Avec la main calculette, on découvre une manière ludique d’effectuer les “grandes” multiplications des tables. En se servant d’un processus digital, on obtient un résultat… assez coûteux en calcul !

Au Cycle 3 : décrire & écrire un algorithme
La main calculette est un programme en quelques étapes. Retenir la séquence d’instructions pour les élèves est assez facile, en revanche, sa verbalisation est plus complexe. L’écriture d’un script en langage naturel est tout à fait appropriée dès le cycle 3.

Au Cycle 4 : de l’algorithme à Scratch
Comme l’indique la figure ci-dessus, le passage du langage naturel à un langage semi-naturel nécessitant plus de rigueur et de précisions est un exercice intéressant et nécessaire dans le processus d’apprentissage de construction de programme dans un langage informatique.

Mémoriser ses tables reste encore problématique pour une bonne partie des élèves. L’approche manipulatoire peut redonner du plaisir et donc motiver ces élèves en difficulté. Ils se retrouvent à faire beaucoup de calculs pour une simple multiplication ; mais faire appel à des notions tel que “retrancher”, “ajouter”, “effectuer le produit de” est important car ces notions ne sont pas encore bien “installées”.

Prolongement : du calcul Littéral au Soroban [3] pour l’Anzan [4] !
En fin de Cycle 4 ou au Lycée, il faut se lancer dans la démonstration à l’aide du calcul littéral (double distributivité) en donnant du sens à la compétence “modéliser”.
Un regard critique pousse vite les élèves à se plaindre de l’efficacité de cette méthode. Il en existe de plus évoluée qui font appel aux abaques Japonais (Soroban) et qui suscitent, à coups sûrs, l’admiration de tous les élèves… comme des professeurs.

Apport du numérique : un boulier ! [5]

Le Verger des Nombres
#carré_du_nombre #boucle #condition #variable #calcul_littéral

Un jardinier souhaite planter 150 arbustes selon un schéma bien précis : un alignement de carrés successifs.

Les plantes sont véritables, nous avons apporté pour l’occasion une cinquantaine de petits pots de caféiers (bourbon pointu) et de théiers (thé de Grand Coude) qui permettent de différencier les pots qui sont ajoutés à chaque itération. Ils parviennent à la solution à l’aide d’une addition répétitive en sept étapes

Au Cycle 3 : La reconnaissance des formes et des suites logiques
Dans un premier temps, les élèves font de la reconnaissance des formes. La reconnaissance de formes (ou parfois reconnaissance de motifs) est un ensemble de techniques et méthodes visant à identifier des motifs informatiques à partir de données brutes afin de prendre une décision dépendant de la catégorie attribuée à ce motif. On considère que c’est une branche de l’intelligence artificielle qui fait largement appel aux techniques d’apprentissage automatique et aux statistiques. Ici il s’agit de différencier les plants de théiers et de cafés, puis de les remplacer par des plots (représentation imagée), première étape vers l’abstraction. Il faut jouer sur différentes représentations pour permettre aux élèves de résoudre les problèmes [6].

Au cycle 4 : donner du sens au calcul littéral et aux itérations
la capacité des élèves à passer de la représentation physique des citronniers à une représentation imagée, pour ensuite identifier le nombre de citronniers à une étape donnée à l’aide d’une expression littérale, est ici recherchée. Donner du sens au calcul littéral en tournant autour des questions comme : “Combien de citronniers en plus d’une étape à l’autre, combien de citronniers au total, combien de citronniers à l’étape n ?”. Ces questions peuvent faire l’objet d’un programme informatique en Scratch [7] ou Python.

Le triangle de Sierpinski
#angle #côté #droite #segment #point #sommet #milieu #mesure #centimètre #mètre #unité #règle #corde #compas #cercle #équilatéral #polygones #fraction #aire #puissance

On ne présente plus cette fameuse fractale : Il peut s’obtenir à partir d’un triangle “ plein ” , par une infinité de répétitions consistant à diviser par deux la taille du triangle puis à les accoler en trois exemplaires par leurs sommets pour former un nouveau triangle.

Au Cycle 3 : verbaliser l’algorithme en travaillant la géométrie
Les élèves perçoivent l’algorithme récursif au bout de quelques itérations. La verbalisation de cet algorithme est ici l’objectif principal retenu pour la partie algorithmique : le mot “algorithme” peut d’ailleurs prendre tout son sens à l’issue de cette activité.

Du Cycle 4 au Lycée : aborder l’appel de fonction et la récursivité
Une figure fractale est un objet mathématique, telle une courbe ou une surface, dont la structure est invariante par changement d’échelle. Dans la fractale de Sierpinski, les diverses formes du programme de l’énoncé, plongent les élèvent au coeur des différents niveaux de langage d’un algorithme. Objectif ultime : la création d’un programme avec scratch [8] ou avec un logiciel de géométrie dynamique.

La méthode de coloriage du triangle est un défi : doit-on retirer ou ajouter de la couleur ? Fixe-t-on à l’avance le nombre d’itération ou se laisse-t-on la liberté de prolonger indéfiniment l’algorithme ?!

Prolongement : l’aire limite du côté obscure...
En cherchant à s’intéresser aux portions d’aires noircies du triangle, on aborde les fractions, les puissances et le calcul littéral menant à la notion de limite est des plus fascinant pour les élèves .

Apport du numérique : le jeu du Chaos ! [9] [10]

Les arbres fractales
#règle #rapporteur #angle #transformation #agrandissement #réduction

La nature récursive d’un arbre est évidente : la branche d’un arbre est la réplique miniature de l’ensemble : pas identiques, mais de forme similaire.

Au Cycle 3 : reconnaître des motifs dans le dessin, progresser par essai-erreur
Prolonger la figure fractale au delà de l’étape trois est souvent source d’erreurs et de nombreux essais. On ne recherche pas le dessin exact mais plutôt une forme approchée schématique et authentique. C’est l’occasion de débugger, de mettre en lumière des ruptures dans l’exécution de l’algorithme de départ et de chercher à quel moment a-t-on dérogé aux instructions données initialement ?

Cet atelier fait appel à la notion d’angle dont la construction n’est pas abordée au primaire. En revanche, par le biais des nombres et de l’histoire (controversée) de leur écriture, on aborde la reconnaissance des angles sur les chiffres. Les nombres 1, 2 et 3 dessinés à côté des trois premières étapes de l’arbre fractale à deux branches ont été dessinés de manière étrange…

Chercher à découvrir le dessin des chiffres suivants en respectant le nombre d’angles est un “petit” jeu qui ravit les petits et les grands.

Du Cycle 4 au Lycée : passer de la vitesse de la craie à celle du processeur, jouer avec les paramètres
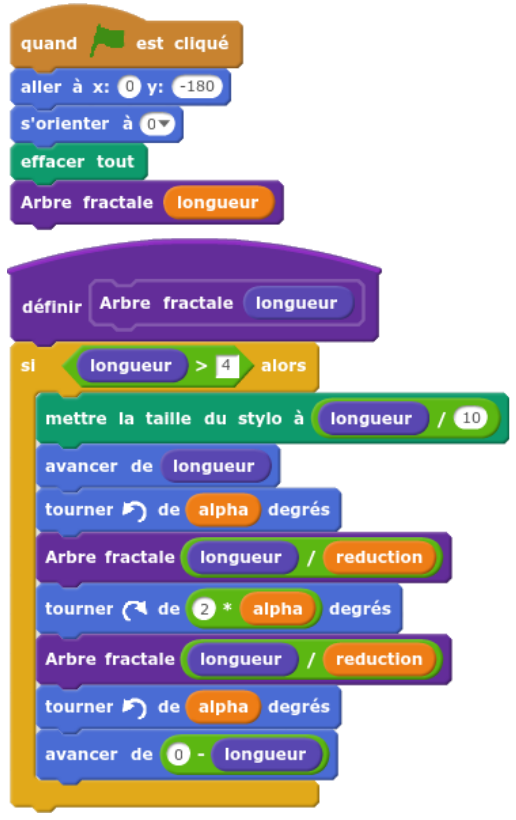
Tout comme le triangle de sierpinski, nous avons ici une figure fractale qui nous permet de retravailler la reconnaissance des formes et de vérifier si le lien a été fait entre les deux activités. La encore, il est possible de prolonger cette activité avec Scratch [11]. Algorithmique et programmation : L’arbre fractale à deux branche est un programme qui peut s’écrire de manière séquentielle et qui fait appelle aux variables et affectations, aux instructions conditionnelles, aux boucles, aux fonctions. Sa traduction en Python peut aussi permettre d’amener les élèves à découvrir la récursivité.

Analyse a posteriori

Qu’avons nous constaté ?

Le plaisir de jouer au coeur de l’apprentissage

Les professeurs dans leur ensemble ont été conquis par la mise en activité dans la bonne humeur des élèves. Le public (enfants et adultes) s’accroche lorsqu’on met leurs sens en éveil. Nous avons été les premiers agréablement étonnés de voir des élèves de primaire s’essayer au calcul littéral ou traduire sans qu’ils ne le sachent, leurs actes en séquence d’instructions. Les élèves de SEGPA, rebutés à l’idée de passer une matinée complète à faire des maths, se sont pris aux jeux et ont pris du plaisir à raisonner et à calculer.

Passer par les écrits intermédiaire pour construire le savoir.

Les compétences mathématiques travaillées deviennent plus naturelles en proposant différentes représentations de la notion abordée ou à venir. La maîtrise des différents registres de langage est un acte pédagogique à travailler régulièrement. La phase de verbalisation de ce que nous avons réalisé ensemble prend alors sens. Nous avons vu des élèves écrire sur le sol leur approche de manière non imposée. Une discussion peut alors s’opérer entre l’enseignant (le médiateur) et l’élève (l’acteur principal) pour rendre plus explicite leur recherche et tenter de comprendre le processus mis en oeuvre. L’échange entre pairs devient naturel et productif.

De la nécessité de passer par l’algorithmique débranché

L’approche kinesthésique, première étape du processus cognitif

Le passage par le toucher est indispensable avant la phase de verbalisation d’une notion. À chaque fois, nous avons constaté que la manipulation d’objets est essentielle pour garder les élèves concentrés sur l’activité proposée. Avec les PACOM (Problème À Ciel Ouvert Mathématiques), nous avons expérimenté la mise en oeuvre d’ateliers où l’algorithmique et la pensée informatique commencent par de la manipulation d’objets… concrets (de plantes, de clous…) ! Ces objets sont ensuite représentés à l’aide d’images (de plots, de points…). Et après seulement apparaît l’abstraction (calcul littéral, utilisation des affectations de variables…). La notion d’algorithmique et de programmation peut alors prendre sens dans les processus cognitifs de nos élèves.

Les concepts s’approprient avec la langue orale : les Maths c’est du français !

Nous avons remis au coeur de l’apprentissage la compétence “communiquer” qui permet aux élèves de surmonter leurs blocages et de verbaliser les étapes et les itérations des problèmes proposés. Ils ont ainsi pu passer du concret à la modélisation en passant par la reconnaissance des formes et la représentation imagée. L’usage d’un registre de langue familier permet de mettre l’élève en confiance avec les notions qu’il manipule. Il ne verra pas d’inconvénient à s’accaparer des termes technique une fois acquis le concept. Maîtrise de la langue française et mathématiques sont étroitement liées : le langage va permettre de construire le savoir.

Jouer, manipuler, s’entraîner et institutionnaliser

Nos expérimentations ne font que commencer. Il reste à définir dans quelles proportions nous devons jouer, manipuler, s’entraîner et institutionnaliser. Comment pouvons nous exploiter au mieux les ressorts de ces différentes phases pour mener nos élèves aux attendus que nous nous somme fixés. Nos apprentis ont besoin d’une approche plus ludique. Une approche kinesthésique nous semble aujourd’hui indispensable voire incontournable.

Évaluation, critères de réussite, modalités d’évaluation individuelle/collective

Exemple d’évaluation par compétences en 3^e pour le triangle de Sierpinski

Exemple d’évaluation par compétences en 5^e pour le verger des nombres

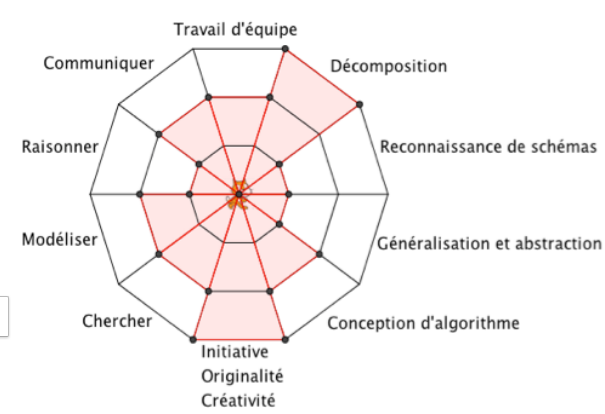
Cette toile pour évaluer… Un visuel simple pour avoir une vue d’ensemble des compétences travaillées : Maîtrise fragile, Maîtrise Satisfaisant - Maîtrise Très bonne

Productions d’élèves : Photos & Vidéos

• Fête de la Science [12]
• Atelier au collège [13]
• Semaine des Mathématiques [14]

Le lien vers le document collaboratif avec fiches élèves & professeurs (commentable) [15]