Théorème de Bézout

Ce théorème de 1776 a un énoncé extrèmement simple :

L'intersection d'une courbe de degré n et d'une courbe de degré p est constituée de np points.

Voici par exemple une conique, en bleu (degré 2) et une cubique, en rouge (degré 3) et on compte bien 6 points à la fois bleu et rouge :

La manière la plus simple pour illustrer le théorème de Bézout est le cas où les courbes sont de degré 1, c’est-à-dire deux droites : Chacun sait que deux droites ont toujours un point commun... sauf si elles sont parallèles ! Dans ce cas on dit que leur point commun est à l’infini et on fait de la Géométrie projective. Le théorème de Bézout devient alors

L'intersection d'une courbe de degré n et d'une courbe de degré p est constituée de np points, à distance finie ou infinie.

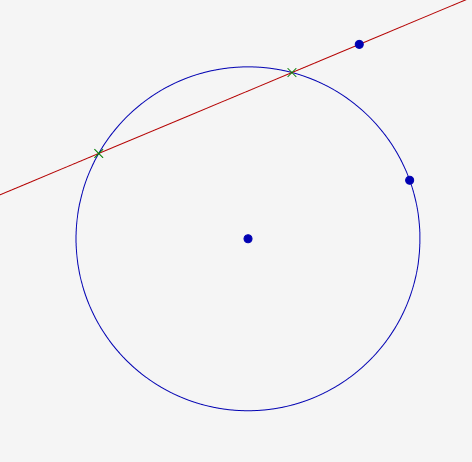
Dans le cas d’une droite et d’un cercle, comme $1 \times 2=2$, Bézout prédit deux points communs comme on le voit sur la figure ci-dessous, où il est conseillé de manipuler les points bleus :

Comme on peut le voir, la droite peut très bien être tangente au cercle, et dans ce cas la manipulation de la figure ci-dessus montre que les deux points verts collisionnent (un seul point compté deux fois), mais aussi les deux points semblent disparaître parfois, auquel cas on dit qu’ils sont devenus imaginaires ! [2]. C’est Chasles qui semble avoir trouvé un formalisme pour rendre tout ça rigoureux. L’énoncé de Bézout devient alors

L'intersection d'une courbe de degré n et d'une courbe de degré p est constituée de np points réels ou imaginaires, distincts ou confondus, à distance finie ou infinie.

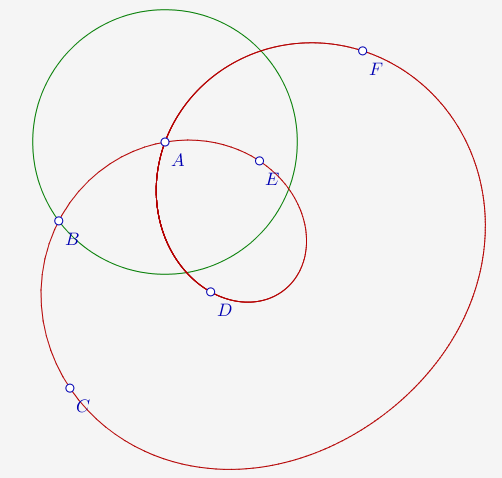
Voyons ce que cela donne dans le cas de deux cercles :

Il y a les deux points communs à chaque cercle et à la droite passant par ces points communs [3] qui sont soit réels (en vert) soit imaginaires (donc invisibles) et deux autres points qui sont

• • imaginaires
  • à l’infini
  • communs à tous les cercles du plan

Ces points s’appellent les points cycliques. Ils sont conjugués. Il y a deux raisons pour lesquelles on ne les voit pas :

1. Ils sont à l’infini
2. Ils sont imaginaires.

Les points cycliques sont notés en général I (d’affixe i×∞) et J (d’affixe -i×∞)

On peut définir un cercle comme suit :

On appelle cercle, une conique qui passe par les points cycliques I et J.

Alors, comme il faut 5 points pour définir une conique, il en faut 3 (5 moins les deux points cycliques) pour définir un cercle...

On appelle cyclique une courbe passant par les points cycliques I et J

Ainsi, un cercle est une conique cyclique. Les courbes cycliques les plus étudiées sont les cubiques cycliques. Comme il faut 9 points pour définir une cubique, il en faut 7 pour définir une cubique cyclique. Et donc par 6 points il ne passe qu’une cubique unicursale [4]. Une propriété intéressante des cubiques cycliques unicursales est que leur inverse par rapport à un cercle centré sur leur point double est une conique. Ce qui permet assez facilement de définir une macro CarMetal pour construire la cubique unicursale passant par A, B, C, D, E et F et ayant A pour point double : Il suffit de construire le cercle de centre A passant par B (qui est donc son propre inverse par rapport à ce cercle), de rajouter les inverses C’, D’, E’ et F’ de C, D, E et F par rapport à ce cercle : L’inverse de la conique passant par B, C’, D’, E’ et F’ est la cubique cherchée.

Une fois la construction faite, il suffit de cliquer sur « créer une macro », puis de sélectionner A, B, C, D, E et F (dans cet ordre) comme objets initiaux, et le lieu comme objet final. La macro est téléchargeable en cliquant-droit sur ce lien :

et en remplaçant son extension par « .mcr » Cependant le lieu n’est pas de très bonne qualité, même en augmentant le nombre de points qui le définissent.

Mais CarMetal permet de représenter des lignes de niveau de fonctions à deux variables, et moyennant l’inversion manuelle de la matrice des coefficients d’une cubique, on peut définir une cubique par 9 points. Voici la macro, élaborée en 3 demi-journées (dont la moitié à corriger des erreurs) avec la méthode du pivot :

Pour l’utiliser, c’est un peu compliqué : On sélectionne la macro, on clique sur les 9 points (créés ou non) puis on renomme les coefficients qui apparaissent a, b, c, etc. jusqu’à i. Ensuite on crée une fonction de deux variables, et dans le corps de la fonction on écrit :

a*x^3+b*x^2*y+c*x*y^2+d*y^3+e*x^2+f*x*y+g*y^2+h*x+i*y-1

Puis on efface les coefficients a, b, c etc.

Loi de groupe sur une cubique

D’après le théorème de Bézout, si A et B sont deux points sur une cubique, la droite (AB) recoupe la cubique en un point P unique, à distance finie ou infinie, éventuellement égal à A ou B. Alors si E est un point fixé sur la cubique, l’unique point d’intersection de (EP) et de la cubique est noté A+B car la loi qui, à A et B, associe A+B, a toutes les propriétés d’une loi de groupe commutatif. Cette loi de groupe a des applications aussi diverses que surprenantes, par exemple en arithmétique : Voir à Courbe elliptique.

Cubiques et triangle

La cubique passant par 9 points remarquables du triangle est presque à coup sûr, elle-même remarquable : Voir à ce sujet

• le diaporama que voici
• le site de Bernard Gibert
• Ce dossier CaRMetal (le diaporama qui était en ligne) :