Nous vivons tellement entourés d’ordinateurs qu’on a du mal à imaginer une époque où il n’y avait pas du tout d’ordinateurs. Or dans les années 1930 (donc une décennie avant la fabrication des premiers ordinateurs) des chercheurs ont réussi à définir ce que devrait être un ordinateur, et prévoir ce que ceux-ci allaient être capable de faire. Il va de soi que les résultats de leurs recherches sont toujours d’actualité...
Church
Alonzo Church était persuadé que ce qu’on peut raisonnablement appeler un calcul doit appartenir à l’une des catégories suivantes :
- L’écriture d’un zéro : $(x_1,x_2,...,x_n) \mapsto 0$ (un exemple classique est visible au bas de cette page)
- L’incrémentation d’un entier : $x \mapsto x+1$ (c’est la fonction "successeur" de Peano)
- L’oubli de certaines variables auxiliaires : $(x_1,x_2,...,x_i,...x_n) \mapsto x_i$ (géométriquement c’est une projection sur une droite)
- Le calcul par récurrence : $g(...,x+1)=f(...,x)$
- La recherche de la plus petite solution d’une équation à plusieurs variables, l’une des variables étant alors considérée comme fonction des autres.
- La composition d’opérations des types précédents.
Pour formaliser cette définition d’une fonction calculable, Church a inventé un système formel appelé le lambda-calcul. Des langages de programmation très sérieux comme Haskell et Objective Caml sont basés sur ce lambda-calcul.
Une version moderne de l’énoncé de la thèse de Church serait alors celui-ci :
| Une fonction de $\N^n$ dans $\N^p$ est calculable si et seulement si il existe un programme en OCaml qui la calcule. |
Autrement dit, OCaml est un calculateur universel : Il peut calculer tout ce qui est calculable, et seulement cela.
Turing
Au même moment, Alan Turing, un ancien champion d’athlétisme britannique, réfléchissait lui aussi à ce qu’est un calcul. En se basant sur la manière dont on effectue une multiplication avec le crayon et le papier, il en est arrivé à définir un calcul comme une suite d’opérations simples choisies parmi les suivantes :
- Lire un symbole (un chiffre) ;
- mémoriser quelques chiffres dépendant de celui qu’on vient de lire et de ceux qu’on avait mémorisés précédemment (Turing appelait ça « le cerveau change d’état »)
- écrire un chiffre, éventuellement en effaçant celui qui est là ;
- bouger les yeux (pour aller regarder un autre chiffre ou écrire le résultat d’un calcul intermédiaire dans un coin de la feuille).
Le génie de Turing c’est d’avoir été convaincu que tout calcul, et pas seulement les opérations apprises à l’école, se ramène à cette méthode. Et il a imaginé des machines constituées d’une tête de lecture avec une mémoire finie, et d’une bande infinie, sur laquelle la tête peut se déplacer, lire et écrire des symboles tout en changeant d’état : La célèbre machine de Turing. Voici comment la simulation de Princeton vérifie que les parenthèses d’une expression algébrique sont correctement placées :
On ne peut s’empêcher de constater la ressemblance avec le fonctionnement d’un ribosome (à ceci près que la bande de lecture du ribosome - l’ADN , est séparée de sa bande d’écriture - la protéine)...
En 1936, Turing publie un article dans lequel il affirme le résultat suivant :
| Une fonction est calculable si et seulement s’il existe une machine de Turing qui la calcule. |
Cette affirmation semble contradictoire avec la définition d’Alonzo Church. Mais l’année suivante, Turing est parti pour un séjour à Princeton où il a suivi les cours de Church, et ils ont démontré l’équivalence de leurs définitions, en simulant du lamda-calcul par machine de Turing, et une machine de Turing par le lambda-calcul. D’où la thèse de Church-Turing :
| Toute définition raisonnable de la calculabilité est équivalente à celle de Turing (ou de Church). |
Dans son article de 1936, Turing a également étudié le problème de l’arrêt des machines de Turing : La fonction booléenne qui, à un algorithme donné, associe 1 si la machine de Turing qui calcule cet algorithme s’arrête un jour, et 0 si elle ne s’arrête jamais, est-elle calculable ? Autrement dit, existe-t-il une machine de Turing U qui calcule cette fonction ?
Pour répondre à cette question, Turing a utilisé la numérotation de Gödel :
Dans l’exemple ci-dessus, la description de la machine de Turing (le programme) peut être écrite par un texte :
| 0R)X1 |
| 0R##2 |
| 1L(X0 |
| 1L##4 |
| 2L##3 |
| 2L((4 |
| 3Y |
| 4N |
Ce texte peut ensuite être transformé en une suite de nombres, avec la correspondance suivante :
| 0 | 1 | 2 | 3 | 4 | L | R | # | ( | ) | X | Y | N |
| 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
La suite de nombres commence par 3, 15, 21, 23, 5, 3, ...
Ensuite on représente cette suite d’entiers par un seul entier, égal à 2 puissance le premier, fois 3 puissance le second, fois 5 puissance le troisième, etc. Par exemple, $2^3 \times 3^{15} \times 5^{21} \times 7^{23} \times 11^5 \times 13^3 \times ...$
Les nombres de Gödel sont très grands mais l’unicité de la décomposition en facteurs premiers permet de faire du décodage. Alors, si $n \in \N$, on note $\varphi(n)$ le nombre, 0 ou 1, que fournira U si on lui soumet $n$. On peut considérer U comme la machine de Turing qui calcule $\varphi$. Turing modifie alors U pour obtenir une machine V qui, lorsqu’on lui soumet un nombre $n$, calcule 1 si $\varphi(n)=0$ et boucle sans fin si $\varphi(n)=1$. Alors, en soumettant à V son propre numéro de Gödel, la machine V s’arrêtera si et seulement si elle boucle sans fin. En langage moderne, on dirait que V plante si et seulement si elle ne plante pas. Cette contradiction montre par l’absurde la nonexistence de U :
| Il n’existe pas d’algorithme permettant de savoir si un algorithme s’arrêtera un jour. |
Le génie de Turing lui a valu une deuxième carrière dans l’espionnage, en étant le tout premier cracker (informatique) de l’histoire : Chargé de présider l’unité de kryptographie consacrée à la kryptanalyse d’Enigma, sa rapidité a fait de lui un héros de la Seconde Guerre mondiale. Après la guerre, il a eu la joie de voir les premiers ordinateurs qui étaient une application de ses recherches, et il a conçu l’un des premiers programmes de jeu d’échecs. Condamné en 1952 pour "sodomie", il a accepté la castration chimique, un traitement lourd qui a provoqué chez lui une grave dépression. Aussi lors de son décès en 1954, après avoir mangé une pomme au cyanure de son jardin, a-t-on parlé de suicide.
Il a fallu 55 ans pour que Gordon Brown présente publiquement, au nom du gouvernement britannique, ses excuses à la famille Turing, reconnaissant enfin que l’homosexualité n’est pas un crime chez les scientifiques espions...
Markov
À la même époque que Church et Turing, Emil Post lui, affirmait que calculer, c’est repérer le premier terme d’une suite (finie) de nombres, puis ajouter d’autres nombres à la fin de cette suite, lesquels dépendent de celui qu’on vient de repérer, et que d’ailleurs on efface. On appelle ceci un tag system. En fait, il est facile de simuler ce comportement avec une machine de Turing, comme le montre l’exemple suivant, qui effectue la multiplication de deux entiers naturels écrits en « base 1 » :
Nouvelle version de la thèse de Church-Turing : Une fonction est calculable si et seulement si on peut obtenir ses valeurs en jouant à cette version numérique du jeu de cadavres exquis.
En 1954, Markov a constaté que la réécriture (informatique) ressemblait à un calcul. Il a émis l’hypothèse que calculer, c’est faire de la grammaire formelle. Et démontré que c’est effectivement le cas. Ce qui n’est pas surprenant quand on pense qu’on peut interpréter le lambda-calcul en termes de réécriture.
Des interpréteurs en ligne du système combinatoire de Markov figurent ici et ici. En fait on peut traduire de façon moderne la version markovienne de la thèse de Church-Turing :
| Une fonction est calculable si et seulement si on peut la coder par une RegExp. |
Le calcul de la suite de Fibonacci par un système de Markov est visible dans cet article sur les L-systems.
Machines à registre
S’inspirant des travaux de Post, Hao Wang a cherché dans les années 1950 un langage de programmation le plus simple possible, où des registres (équivalents des cases des machines de Turing) en nombre inifini peuvent être uniquement incrémentés, décrémentés, testés et pointés.
Un descendant plus récent de cette recherche est le langage Brainfuck, ne possédant que 8 instructions, et la version la plus classique de la thèse de Church-Turing s’exprime en langage moderne par :
| Une fonction est calculable si et seulement s’il existe un programme écrit dans le langage Brainfuck qui la calcule. |
On démontre ceci en simulant une machine de Turing par un programme en Brainfuck, et en simulant un interpréteur Brainfuck par une machine de Turing. Ceci revient à dire que le langage Brainfuck, malgré sa simplicité, est un calculateur universel.
Des exemples peuvent être vus en mode pas-à-pas avec cet interpréteur en ligne. Essayer par exemple le calcul des nombres de Fibonacci... Celui-là n’est pas mal non plus (on y apprend à additionner ou multiplier des nombres). Ne pas oublier le plus graphique d’entre eux : Celui d’Enigma...
Pour montrer la relative complexité des programmes Brainfuck, voici un interpréteur Brainfuck écrit en Brainfuck par Daniel Cristofani, et affiché avec coloration syntaxique :

autres calculateurs universels
Automates cellulaires
L’idée que des automates cellulaires pourraient eux aussi calculer tout ce qui est calculable, semble remonter à un autre pionnier des ordinateurs : John Von Neumann. Mais le premier exemple connu est le jeu de la vie de John Conway. En effet, une machine de Turing a été simulée dans le jeu de la vie. On peut la voir dans l’excellent logiciel Golly. Ce genre de résultat est à la base du best-seller de Stephen Wolfram.
Algorithmes diophantiens
On dit qu’une fonction est diophantienne si elle est caractérisée par une équation diophantienne. Par exemple, la fonction racine carrée est diophantienne parce que
$$y=\sqrt{x} \Leftrightarrow x-y^2=0$$
Dans les années 1960, Yuri Matiyasevich a démontré qu’une fonction est calculable si et seulement si elle est diophantienne. Autrement dit, résoudre des équations diophantiennes, c’est faire des calculs universels. Par exemple,
- Les valeurs positives prises par le polynôme $2xy^4+x^2y^3-2x^3y^2-y^5-x^4y+2y$, pour $x$ et $y$ entiers, sont les nombres de Fibonacci : La suite de Fibonacci, que l’on sait Turing-calculable, est donc aussi Diophante-calculable. C’est exactement ce que dit la thèse de Matiyasevich...
- De même, il existe un polynôme à 26 variables dont l’image est l’ensemble des nombres premiers :
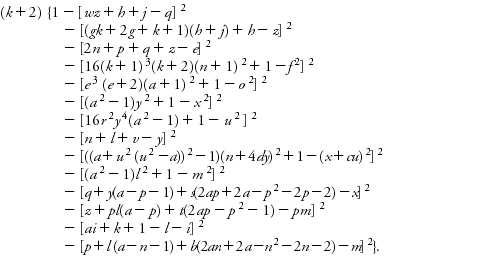
Ces deux polynômes sont dûs à J.P. Jones.
Machines de Turing
On peut aussi simuler une machine de Turing avec une machine de Turing... Cette idée est dûe à Turing lui-même, qui a créé une machine de Turing capable d’émuler le fonctionnement de n’importe quelle autre machine de Turing. On appelle ce genre de machine une machine de Turing universelle. Dans les années 1960, Marvin Minsky a trouvé une autre machine de Turing universelle (7 états, et un alphabet de 4 symboles, soit 28 sommets pour son graphe). Puis c’est Stephen Wolfram qui en a trouvé une autre, plus simple que celles de Minski et de Turing (2 états, alphabet de 5 symboles, soit un graphe de 10 sommets), et encore une autre, appelée (2,3) car elle a deux états et trois symboles (donc 6 sommets pour le graphe ; il est peu probable qu’on puisse faire mieux, ceci en vertu d’un théorème de Minsky). Dans son livre, il pose la question de la démonstration : Est-ce vraiment une machine de Turing universelle ? Avec humour, il a émis l’hypothèse que le temps que mettra la communauté mathématique à démontrer ce résultat n’est peut-être pas calculable... Puis en 2007, il a proposé un prix de 25 000 dollars à celui qui le premier, confirmera ou infirmera cette conjecture. En tentant de l’infirmer, Alex Smith a démontré que la machine (2,3) de Wolfram est universelle, en un peu plus d’un mois, à l’âge de 20 ans. Ce génie est déjà cité dans l’article sur le jeu Enigma.
Voici ce que produit la machine en question sur une bande vide (la machine n’ayant pas d’état « halt », est condamnée à « planter » quelles que soient les données entrées ; les données en question représentant le codage d’une machine de Turing) :
Turmites
Une turmite est une machine de Turing qui peut se déplacer sur un casier bidimensionnel, au lieu de la bande avec des cases contigües. L’exemple le plus célèbre est la fourmi de Langton, et en dehors de l’aspect esthétique dû à ce que le terrain de jeu est un damier, le plus intéressant est de voir comment des turmites interagissent. Le logiciel boppers de l’auteur de SF Rudy Rucker est fourni avec des exemples de turmites pouvant subir des mutations génétiques aléatoires, et vivant dans un monde de compétition pour leur survie. Ce sont donc de bons exemples pour illustrer la complexité d’un écosystème.
Sokoban
Le plus original des calculateurs universels, c’est encore un jeu : Sokoban. Le principe de la simulation de machines de Turing dans Sokoban est résumé dans cet article.

Commentaires