L’article a été publié dans les Mémoires de l’Académie des Sciences de Berlin en 1741, sous le titre Calcul de la probabilité du jeu de rencontres. Voici la version pdf de l’article (que par chance, Euler a écrit en Français [1]) :

Dans le paragraphe 1, Euler explique brièvement la règle du jeu. Dans les paragraphes 2 à 4, il explique que seul le deuxième jeu doit être mélangé, le jeu 1 peut rester dans l’ordre, ce qui simplifie son analyse. Dans les paragraphes 5 à 14, il analyse dans le détail les jeux à 1, 2, 3 ou 4 cartes, tout simplement en faisant la liste des permutations, et en comptant les permutations pour lesquelles au moins un élément n’a pas bougé. Dans le paragraphe 15, il explique que pour 5 cartes, vu que 5 !=120, ça commence à devenir un peu difficile... Aussi dans le paragraphe 16, évoque-t-il la nécessité de trouver une sorte de relation de récurrence, qu’il va chercher dans pratiquement toute la suite de l’article.

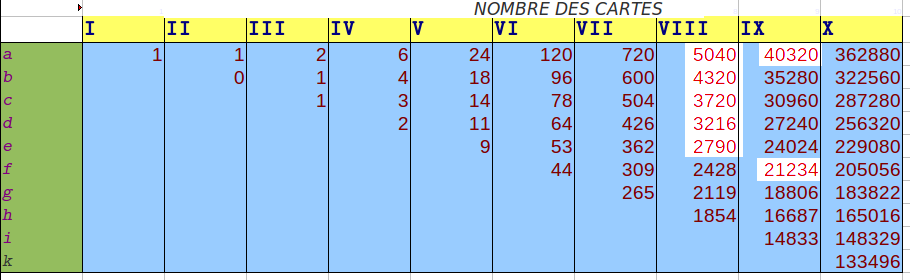
Dans les paragraphes 17 et 18, il rappelle ce que sont les factorielles et ce qu’elles viennent faire dans cette histoire. Les paragraphes 19 à 21 font l’objet d’une remarque discrète mais importante : Le nombre de permutations pour lesquelles il y a une rencontre à une position donnée est la factorielle de n-1, n étant le nombre de cartes. En effet, une fois la carte k bien placée, il reste (n-1) ! permutations correspondant aux mélanges des n-1 cartes restantes. Mais dans les paragraphes 22 à 34 (avec une coquille dans le paragraphe 31 : M au lieu de M’), il précise que parmi ces (n-1) ! permutations, on ne doit pas compter celles pour lesquelles il y a eu une rencontre auparavant, et arrive donc à la constitution dans le paragraphe 35, de ce tableau :

Par exemple, pour 9 cartes, il y a 40320 permutations pour lesquelles la carte numéro 6 est bien placée. Mais on soustrait les permutations des 8 autres cartes sont elles-mêmes bien placées, lues dans le tableau à la colonne précédente. Le nombre 40320 se lit pour la carte 1, et les autres nombres, dans la colonne 8, sont additionnés entre eux, puis soustraits à 40320 pour avoir les 21234 permutations qui font gagner A à la 6^e carte (et pas avant).

Pour construire le tableau ci-dessus, on remplit la ligne 3 (indiquée a) avec les factorielles des nombres entiers (qui sont cachés ligne 1 pour mettre leur traduction en chiffres romains dans la ligne 2). Puis dans la cellule C4, on place la formule

=C$3-SOMME(B$3:B3)

pour soustraire la somme de gauche à la cellule du haut, et cette formule a juste été copiée dans le reste du tableau (du moins là où elle a un sens) pour compléter celui-ci. Au passage on remarque une coquille dans la cellule Xc du tableau d’Euler : 387280 au lieu de 287280...

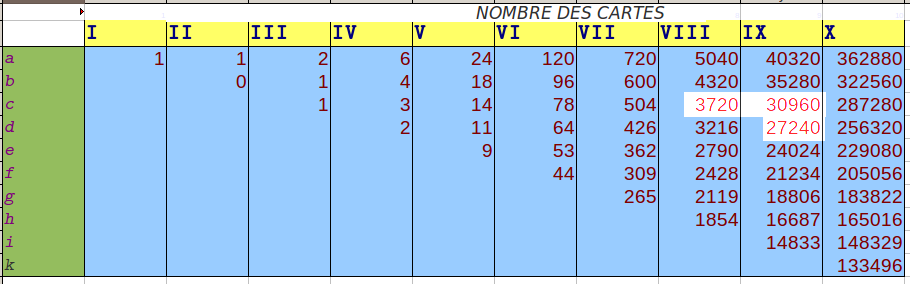
Puis dans le paragraphe 37, Euler transforme la formule récurrente avec sommes ci-dessus, en une formule avec différence : Il constate que chaque nombre du tableau est la différence entre celui d’au-dessus et celui d’au-dessus à gauche (un peu comme le triangle de Pascal mais avec soustractions) :

Ci-dessus on a mis en exergue le fait que 27240 n’est pas seulement égal à 40320-(5040+4320+3720), mais aussi à 30960-3720. Exercice : Peut-on démontrer ceci ?

Le tableau du paragraphe 35 peut donc aussi se faire, après avoir mis les factorielles dans la ligne 3, en copiant la formule

=C3-B3

à partir de la cellule C4.

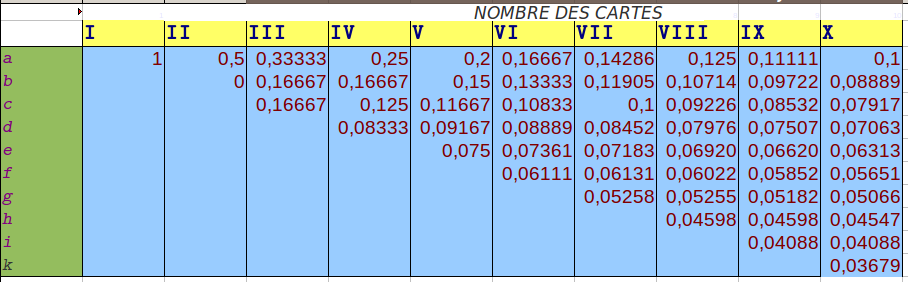
Cette formule de récurrence est assez simple pour qu’on puisse l’utiliser dans le tableau des probabilités, qu’on peut obtenir tout simplement en divisant chacun des nombres entiers ci-dessus par la factorielle du nombre de cartes :

On retrouve ligne a du tableau ci-dessus le fait que le quotient de la factorielle de n-1 par celle de n est l’inverse de n, ce qu’Euler rappelait dans le paragraphe 36.

En divisant par la factorielle de n, la relation de récurrence avec soustractions donnée ci-dessus, on obtient celle qu’Euler donne dans le paragraphe 38 de son article, et qui se traduit dans le tableur, par la formule suivante à mettre dans la cellule C4 :

=C3-B3/(B$1+1)

à copier vers la droite et vers le bas, après avoir mis les inverses des entiers dans la ligne 3 du tableau. On obtient alors exactement le même tableau que ci-dessus. Pour avoir la probabilité que A gagne avec n cartes, on doit additionner les probabilités de la colonne n, ce qui peut se faire en cliquant sur le bouton $\Sigma$. Mais pour obtenir ces probabilités, Euler ne s’arrête pas là : Il veut encore une relation de récurrence pour calculer la probabilité de gain de A pour chaque valeur de n, et même la limite pour n tendant vers l’infini !

Dans les paragraphes 39 à 42, il donne l’expression littérale de la probabilité de gain à la première carte (fonction de n), puis à la deuxième carte, etc. et voit apparaître le triangle de Pascal à nouveau, ce qu’il semble considérer comme un résultat classique (« Pour peu qu’on réfléchisse sur la formation de ces formules », écrit-il au paragraphe 42), ce qui est sans doute le cas avec les tableaux de différences itérées comme celui du paragraphe 35. En effet les formules du paragraphe 42 sont à la base de la formule de Newton-Cotes, qui comme son nom l’indique, remonte à Isaac Newton.

Par exemple, au troisième coup, on a d’après la formule de récurrence précédente,

$$\frac{1}{n}-\frac{1}{n(n-1)}-\frac{1}{n}\left(\frac{1}{n- 1}-\frac{1}{(n-1)(n-2)}\right)=\frac{1}{n}-\frac{2}{n(n-1)}+\frac{1}{n(n-1)(n-2)}$$

Mais on n’a pas encore fini : Il reste à additionner les colonnes du tableau du paragraphe 42, et si les dénominateurs sont des produits de n et de ses prédécesseurs, les numérateurs sont des sommes (au signe près) de termes du triangle de Pascal, qui sont elles-mêmes les termes suivants (d’un cran à droite) dans le même triangle de Pascal. Par exemple $1+2+3+4+...+n=\frac{n(n-1)}{2}$. Euler semble là aussi considérer ce fait comme connu (il ne fait que l’affirmer dans le paragraphe 43, sans même esquisser la démonstration). Les numérateurs et les dénominateurs se simplifient alors de telle manière que les fractions sont les inverses des factorielles, avec des signes alternés. Euler les donne dans le paragraphe 44, sous forme exacte (en détaillant les sommes sans les effectuer).

Dans le paragraphe 45, Euler analyse les résultats : A a plus de chances de gagner si le nombre de cartes est impair que s’il est pair (du moins le nombre pair suivant). Dans le paragraphe 46, il explique comment calculer la probabilité du contraire de l’évènement « A gagne » à partir de la probabilité de l’évènement lui-même. Et il récapitule numériquement le tout dans le tableau du paragraphe 47 :

(On remarque que pour 14 et 15 cartes, Euler tronque le dernier chiffre au lieu de l’arrondir). On ne peut qu’admirer la précision des calculs menés sans outil informatique par Euler... Il en déduit qu’à 9 décimales près, la convergence est assurée à partir de 12 cartes, et que du point de vue des probabilités, le jeu à 13 cartes (classique à l’époque) équivaut à un jeu à 52 cartes (cité par Euler au paragraphe 50) ou au jeu à un nombre infini de cartes (paragraphes 48 à 50).

Par approximations rationnelles, Euler retrouve alors le pari à 12 contre 7 que des joueurs invétérés ont du lui indiquer, sans doute en lui demandant d’où venaient ce 12 et ce 7 (n’oublions pas que le parcours du cavalier avait été découvert aussi lors d’un voyage en diligence). Il signale aussi le résultat un peu surprenant selon lequel la probabilité de gain de A est proche de $1-\frac{1}{e}$.

Étude du problème par des contemporains d’Euler

Le premier à avoir publié sur le sujet est Pierre Raymond de Montmort dans son livre publié en 1713 (soit 28 ans avant l’article d’Euler). De Montfort explique que les 13 cartes sont extraites d’un jeu de 52 (par exemple, un joueur peut prendre les carreaux et un autre, les piques, en numérotant les valets, dames et rois par 11, 12 et 13). Il calcule les valeurs exactes, en fractions irréductibles, des probabilités de gain de A jusqu’à 13 cartes, et trouve $\frac{109339663}{172972800}$. Il semble avoir fait les calculs par dénombrement puis découvert à partir des fractions, la formule

$$P(A)=\frac{1}{1 !}-\frac{1}{2 !}+\frac{1}{3 !}-\frac{1}{4 !}+...$$

Bien que Jean Bernoulli, bâlois comme Euler, ait pu rencontrer ce dernier, il n’est pas certain qu’Euler ait connu l’article de Montmort avant d’écrire le sien. Il n’y fait pas référence, et n’utilise pas la même méthode pour ses calculs.

La version d’Abraham de Moivre date de 1756, et est donc de 15 ans postérieure à celle d’Euler. De Moivre détaille les calculs pour 6 cartes (en laissant les fractions sans les additionner), puis infère la série alternée à un nombre quelconque de cartes.

En 1771, c’est Johann Lambert, muhlousien donc lui aussi presque voisin d’Euler, qui publie Examen d’une espèce de superstition ramenée au calcul des probabilités. Il cherche à expliquer pourquoi il ne faut pas s’étonner que de temps en temps, les astrologues tombent juste. Il découvre en substance la série du paragraphe 42 d’Euler, et la décrit comme un produit d’Hadamard de la formule du binôme de Newton et d’une suite d’entiers (ceux qui paraissent sur la diagonale du tableau d’Euler) qu’il décortique.

Webographie

• L’article provient du blog d’Euler (chercher à Combinatorics and Probability, et l’article est le deuxième). L’article de Montmort y est évoqué.
• Le site d’un fan où le jeu est traité sous le nom de dérangements. Les autres articles valent eux aussi largement la visite de ce site.
• Un wikilivre consacre une partie de ses chapitres sur la simulation, à des simulations avec Python (langage) et Ruby, de ce jeu. Python en particulier est muni d’un outil de permutation aléatoire qui facilite grandement le protocole d’expérimentation (ici et là).