Algorithmique : les attendus du programme officiel

Les algorithmes seront construits à l’aide du logiciel Algobox version 0.3 et les rendus réalisés à l’aide du logiciel Scratch version 1.4.

Pascal Brachet, qui a réalisé le logiciel Algobox, propose une excellente initiation à l’algorithmique ici.
Les liens sur les images des exemples Algobox conduisent à l’exécution en ligne des algorithmes proposés, Algobox permettant une exportation html de l’exécution de l’algorithme.

Scratch est très intéressant puisqu’il propose un développement très ludique, mais aussi pour son option de « Partage » qui permet d’exporter en ligne sur un site mutualisé tous vos algorithmes. Scratch s’inspire largement du langage Logo mais on attend avec impatience une version qui y incorpore des sous-programmes. Par contre, il permet d’exécuter plusieurs « sprites » (algorithmes) en parallèle. Il permet aussi de faire des algorithmes qui travaillent dans une fenêtre graphique.
On peut espérer un grand enthousiasme de la part de nos élèves « Digital Natives ».

Les liens sur les images des exemples Scratch conduisent donc à une exécution en ligne sur le site du MIT (laboratoire père de Scratch) du programme dont le script est donné.

Les instructions élémentaires

– Déclaration des variables
La plupart des langages de programmation nécessite une phase de déclaration des variables, donc il serait bien de commencer par faire la liste avec les élèves de toutes les variables dont ils auront besoin dans l’algorithme.
Les types de données dont les élèves auront besoin sont au nombre de trois :

1. 1. la variable est du type Nombre
   2. la variable est du type Chaîne de caractères
   3. la variable est du type liste de nombres (ou de chaînes de caractères)

Voici par exemple la liste des variables dont on aura besoin pour résoudre une équation du second degré :

– Affectation
Il s’agit de faire comprendre aux élèves qu’une variable, c’est comme un tiroir dans lequel on range des objets (par exemple des nombres).
Afin de donner de bonnes habitudes aux élèves, ce serait bien de leur faire initialiser leurs variables systématiquement.

– Entrée / Sortie
Si les variables n’ont pas été affectées dans le programme, on pourra les Lire au clavier par exemple. Une variable doit être affichée pour en connaître le contenu.

– Calcul

1. 1. Premier Exemple : transformer des francs en euros
   2. Deuxième exemple : calcul du discriminant d’une équation du second degré :

Boucle et itérateur, instruction conditionnelle

– Calcul itératif Pour ... De ... A ...

Il s’agit ici d’effecteur un calcul itératif, le nombre d’itérations étant connu.

• • Premier exemple : Afficher les inverses des 100 premiers entiers naturels

• • Deuxième exemple : Afficher la somme des inverses des 100 premiers entiers naturels

• • Troisième exemple : Fonction puissance (avec n entier)

• • Quatrième exemple : Afficher les puissances de 2

• • Cinquième exemple : Calcul de la moyenne d’une liste de nombres

– Instruction conditionnelle Si ... Alors ... ( Sinon ... )

En images...

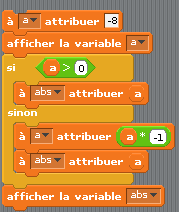
• • Première application du Si ... Alors : la valeur absolue d’un nombre.

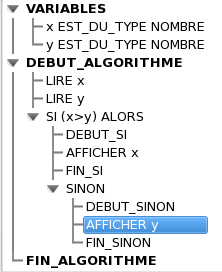
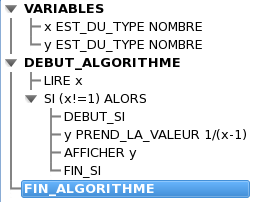
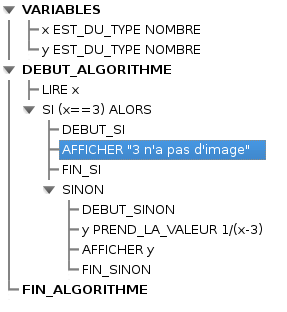
• • Deuxième application : Valeur interdite d’une fonction

• • Troisième application : Résolution d’une équation du second degré

– Calcul itératif avec fin de boucle conditionnelle Tant Que ... Faire ... ou Faire ... Jusqu’à ...

Le calcul itératif va être arrêté à la réalisation d’une condition.

• • Premier exemple : Dessiner une fonction carrée

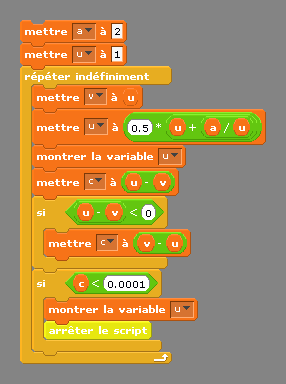
• • Deuxième exemple : La racine carrée d’un nombre par l’algorithme de Héron

• • Troisième exemple : Une suite divergente

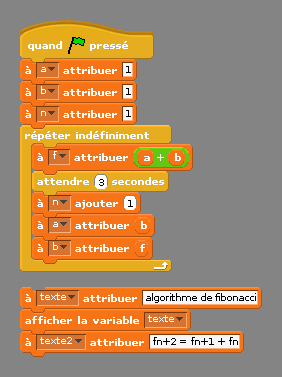
• • Quatrième exemple : Fibonacci

On remarquera que sur cet exemple, il n’y a pas de fin de boucle. Cela peut faire l’objet d’un exercice : faire arrêter le script lorsque le nombre affiché devient supérieur à 1000.

Certains scripts Scratch de cette page sont téléchargeables sur le site du MIT dans l’espace de l’utilisateur nathalierun : http://scratch.mit.edu/users/nathalierun. Il faudra s’enregistrer au préalable.

Un forum en français autour de Scratch est disponible à cette adresse.

Vous trouverez des algorithmes de simulation à cette page :
« Algorithmes, simulations et échantillonnage »

Avril 2017 : découvrir Snap !

Comme prolongement à cet article, je vous propose la lecture de l’article Coder des algorithmes avec Snap ! - Programmation visuelle au lycée, actualisation 8 ans plus tard de ce que représente la programmation visuelle. Snap ! est un langage de programmation similaire à Scratch, qui repose sur les mêmes concepts : programmer des algorithmes en mettant des lutins en scène. Mais Snap ! permet de créer ses propres blocs et est donc mieux adapté à l’enseignement des mathématiques. L’article Coder des algorithmes avec Snap ! vous conduira notamment à une galerie d’images dans laquelle vous pourrez lire, copier et exécuter le code de nombreux algorithmes.