L’activité a été menée en deux étapes :

Étape 1

Le sujet était :

Résoudre par algorithme l’équation ln(x)=1

La description de l’algorithme s’étant faite collégialement et oralement, une bonne surprise a été qu’alors que le groupe 2 a naturellement choisi l’algorithme de dichotomie [1], le groupe 1, quant à lui, a opté pour l’algorithme de balayage, plus facile à implémenter tant sur ordinateur que sur calculatrice [2].

Groupe 1

Après avoir constaté (avec la calculatrice) que ln 2 est plus petit que 1 et que ln 3 est plus grand que 1, plusieurs élèves ont pensé à calculer les logarithmes de 2,1 2,2 2,3 etc. Ce qui a été vite fait au tableur. Par la suite, la traduction en langage algorithmique a été un peu plus dure, mais finalement assez rapide. La moitié des élèves a choisi CaRMetal, l’autre moitié la calculatrice. Voici la version JavaScript :

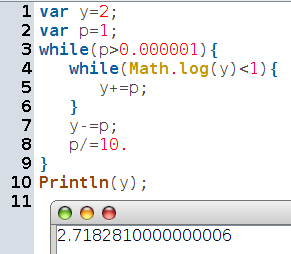
Groupe 2

Après avoir calculé numériquement avec la calculatrice, les logarithmes de quelques entiers, les élèves ont compris que x est entre 2 et 3. Plusieurs ayant pensé naturellement à la moyenne entre 2 et 3 comme meilleure valeur approchée de x, l’algorithme a été rédigé au tableau, par moi, sous la dictée des élèves, puis traduit en langage de programmation au choix des élèves (CaRMetal, Algobox et la calculatrice, celle-ci étant de toute façon testée en complément des autres).

Voici la version JavaScript :

Pour les plus rapides, une version Python a été testée :

Et l’occasion est trop belle pour ne pas montrer la version MathsOntologie :

Quelques explications

La première ligne est la liste des variables (a, b et m) nécessaires. 2 et 3 sont convertis en décimaux parce que par défaut, MathsOntologie calcule sur des fractions, et que dans ce cas les résultats seront peu lisibles. Enfin, pour calculer le logarithme de m, on n’écrit pas ln(m) mais m ln.

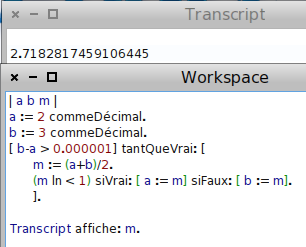
Ensuite, le bouton de la calculatrice [3] a été mis à contribution pour évaluer la précision de l’algorithme.

Étape 2

C’est la semaine suivante que les algorithmes ont été généralisés à d’autres logarithmes que 1 ; pour cela il suffit de remplacer 1 par x et de transformer le tout en fonction [4] :

Groupe 1

Groupe 2

Dans les deux groupes, après avoir fait quelques Println(exp(1)) et autres pour tester, les élèves sont rapidement arrivés à la partie qui les a le plus intéressés : Tester des dizaines de valeurs de x en glissant la souris, et représenter graphiquement les résultats. Pour cela, il a fallu

• Créer un point M sur l’axe des abscisses
• Créer un point P mobile dans le plan
• colorier P en rouge, le rendre petit et gras, cacher son nom (plus rapide à faire qu’à dire...)
• activer la trace de P

puis dans les scripts, remplacer les Println par

x=X("M");
Move("P",x,exp(x));

(lire la valeur de x comme abscisse de M, puis déplacer P de telle manière qu’il reste sur la représentation graphique).

Ensuite, en cliquant sur l’icône représentant un scripts, on choisit le gestionnaire de script, au sein duquel on sélectionne M comme déclencheur de script :

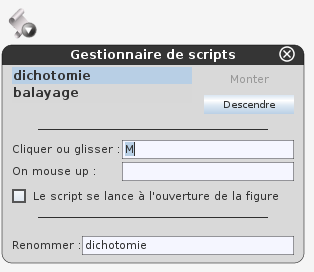
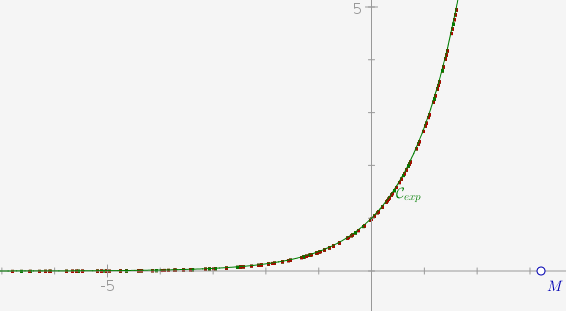
Après cela, il suffit de faire bouger M pour voir apparaître, point par point, une courbe représentant une fonction : La fonction exponentielle :

Pour aller plus loin

Comme CaRMetal se trouve, par un étrange hasard, doté d’une fonction notée elle aussi exp, autant la représenter graphiquement :

La précision des deux algorithmes (surtout la dichotomie) est telle qu’on a du mal à distinguer la « vraie » fonction des algorithmes.

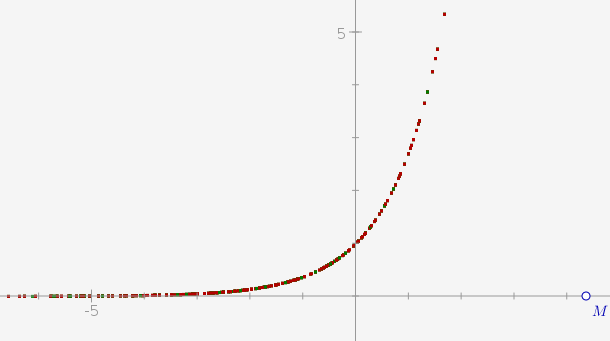
Conclusion

En deux séances d’environ 40 minutes chacune, il faut un peu plus d’une heure pour amener en douceur la notion d’exponentielle. Ce qui montrera des avantages

• lors du cours sur les équations différentielles
• lors du cours sur les nombres complexes
• lors du cours sur les variables aléatoires exponentielles
• lors du cours sur les variables aléatoires normales
• et du coup, en statistiques inférentielles et sur les intégrales.

75 à 80 minutes pas vraiment perdues...