L’idée directrice de cet article est que depuis la console JavaScript de CaRMetal, on peut accéder à toute la puissance du langage Java. Comme on n’a rien sans rien, il est nécessaire de charger dans JavaScript les bibiothèques Java dont on a besoin, ce qui se fait avec
importPackage(NomDuPaquet);Mais c’est le seul effort supplémentaire à fournir ! Après cela on peut jouer du synthé, accéder à toutes les méthodes cachées de CaRMetal, faire communiquer celui-ci avec d’autres logiciels, etc.
Bref, pour en savoir plus que ce qui est montré dans cet article, il faut aller consulter la référence du langage Java...

Précision sur le vocabulaire : Dans cet article, le mot CaRScript désigne un programme en JavaScript destiné à être exécuté sous CaRMetal, alors que le mot CaRAScript désigne la variante où le CaRSCript est lancé automatiquement lors du mouvement d’un point sur la figure.
Bézout
Mais avant d’aller charger des bibiothèques spécialisées de Java, CaRMetal possède 4 fonctions arithmétiques, qu’on peut utiliser dans des expressions de la figure (coordonnées de points, couleurs des objets, ...) :
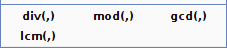
– La fonction div accepte deux nombres (non nécessairement entiers) et retourne le quotient euclidien du premier par le deuxième. Malgré la présentation dans le menu, il faut séparer le dividende du diviseur par un point-virgule et non par une virgule.
– La fonction mod accepte deux nombres (non nécessairement entiers) et retourne le reste euclidien du premier par le deuxième. En utilisant $2 \pi$ comme deuxième nombre, on a la valeur principale d’un angle en radians. La fonction n’est donc pas purement arithmétique.
– La fonction lcm accepte deux nombres et renvoie leur ppcm.
– La fonction gcd accepte deux nombres et renvoie leur pgcd. Par exemple, en créant une courbe implicite et en y entrant l’équation
gcd(x;y)-2
on a la ligne de niveau 2 du pgcd :
qui renseigne sur l’algorithme utilisé...
Cela permet de faire des CaRAScripts consacrés à l’arithmétique.
Premier exemple : Point à mouvement limité
On peut aussi utiliser la récursivité permise par CaRMetal pour limiter le mouvement d’un point P à l’intérieur d’un carré de côté 6, tout simplement en assujettissant ses coordonnées à être réduites modulo 3 (le cadenas évite même d’avoir à taper la formule deux fois) :

Le point P ne peut suivre la souris que si celle-ci reste elle-même dans le carré, sinon il effectue un saut très visible : On a là une manière graphique et dynamique d’introduire le reste euclidien. On peut ensuite représenter graphiquement la fonction mod(x ;3) et commenter l’effet produit sur les réels négatifs...
Deuxième Exemple : Affichage du pgcd des coordonnées
Un moyen simple d’entrer à la souris deux entiers (pour calculer leur pgcd) c’est de prendre les coordonnées (entières) d’un point [1]. Sous CaRMetal, on peut
- commencer par créer un point A ;
- mettre son incrément à 1 (ainsi ses coordonnées seront entières)
- lui donner comme alias
Le pgcd de %x(A)% et %y(A)% est %gcd(x(A);y(A))%
Troisième exemple : Bézout dynamique
Toujours avec un point A de coordonnées entières, on peut mettre l’algorithme d’Euclide étendu dans un CaRAScript acceptant les coordonnées (entières donc) de A, pour afficher dynamiquement dans un objet texte (ci-dessous appelé prems), les nombres u et v réalisant l’égalité de Bézout. Les lignes de code suivantes sont du pur JavaScript, seules les lignes 1 et 2 communiquent avec CaRMetal (en récupérant les coordonnées du point appelant), ainsi que la ligne 19, qui crée un affichage LaTeX donnant la solution de l’équation diophantienne donnée par l’algorithme d’Euclide étendu :

Une fois le CaRAScript recopié, il faut bien entendu l’associer au point A pour que les mouvements de celui-ci mettent à jour, presque instantanément, l’affichage en LaTeX.
Mersenne
Sur un ordinateur 32 bits, chaque entier est codé sur 32 bits signés, donc son écriture décimale comporte au maximum 10 chiffres. Le langage Java possède un objet entier long dont la taille est double du précédent, donc inapte par exemple à gérer les plus grands nombres de Mersenne premiers connus... Pour y remédier, Java possède un objet BigInteger dans la classe math [3], et CaRMetal peut accéder à ses méthodes pour peu qu’on y charge la classe math (c’est l’équivalent du célèbre from math import * de Python). Tous les CaRScripts de cet onglet et du suivant commenceront donc par
importPackage(java.math)Ceci permettra alors de manipuler ces fameux « gros entiers ». Mais avant tout, qu’est-ce que c’est qu’un gros entier ? C’est un entier dont le nombre de chiffres n’est pas limité. Ainsi, même 1 et 2 sont des gros entiers, pour peu qu’on les considère comme tels.
Pour entrer un gros entier, il faut l’introduire comme une chaîne de caractères et le convertir. Par exemple, pour que 1 soit un gros entier, on utilise
BigInteger("1")Si l’entier à convertir en gros entier est caché dans une variable x, on peut convertir celle-ci en chaîne de caractères avec x.toString(), mais cette conversion est faite automatiquement par JavaScript. Comme on doit souvent utiliser 1 comme un gros entier, on peut aussi faire
BigInteger.ONELes quatre opérations sont infixées mais leur nom, écrit en toutes lettres, doit être précédé d’un point. Par exemple, pour vérifier que 2+1=3, on peut entrer
importPackage(java.math);
a=BigInteger(2);
b=BigInteger.ONE;
Println(a.add(b));De même,
– la différence entre a et b s’écrit a.subtract(b),
– le produit de a par b s’écrit a.mulltiply(b) ;
– le quotient euclidien de a par b s’écrit a.divide(b) ;
– le reste dans le même division s’écrit a.mod(b) ;
– la puissance b-ième de a s’écrit a.pow(b) ;
– la même, mais modulo n, s’écrit a.modPow(b,n) ;
– s’il existe, l’inverse de a modulo n est donné par a.modInverse(n) ;
Par exemple, on voudrait savoir combien font $127^{1023}$ modulo $2^{32}$ :
Presque instantanément, on apprend que
$$127^{1023} \equiv 828489599 ~: [4294967296]$$
Les nombres ci-dessus (127 et 1023) ont été choisis premiers de Mersenne. Il résulte du petit théorème de Fermat que pour qu’un nombre de Mersenne soit premier, l’exposant doit lui-même être premier. Mais la réciproque n’est pas vraie. Le test de Lucas-Lehmer permet assez vite de vérifier si un petit nombre de Mersenne est premier, mais avec un grand nombre c’est une autre histoire ! Ceci dit, avec des tests analogues, Java sait tester la primalité d’un nombre arbitrairement grand, avec isProbablePrime (suivi d’un entier qui représente le nombre d’essais ; théoriquement cet entier devrait être supérieur à l’entier à tester pour être certain que l’entier à tester est premier ; concrètement la probabilité qu’il soit composé est négligeable en fournissant environ 10 comme nombre de tests à isProbablePrime).
Le script ci-dessous commence par vérifier que $2^{127}-1$ est premier (avec l’affichage de true), puis que $1023^{31}$ ne l’est pas, puis calcule et affiche l’inverse de $1023^{31}$ modulo $2^{127}-1$ (un nombre de 39 chiffres tout de même) :

L’inverse est 144241301817751220596031080948389737388.
Pour en savoir plus, voir la référence sur les gros entiers.
Fermat
Les nombres de Fermat ont des propriétés intéressantes et relativement peu connues. En particulier, on n’en connaît que 5 qui soient premiers (les 5 plus petits d’entre eux). Et deux nombres de Fermat sont toujours premiers entre eux, les gros entiers de Java permettent de le verifier sur des exemples, tout simplement en calculant leur pgcd. Par exemple, $F_7=2^{128}+1$ et $F_8=2^{256}+1$ sont premiers entre eux :

Et puisqu’ils sont premiers entre eux, il existe deux entiers $u$ et $v$ tels que $u \times F_7 + v \times F_8=1$. Pour les trouver, on peut réécrire l’algorithme d’Euclide étendu pour les gros entiers :

On a instantanément
u=-170141183460469231731687303715884105728
v=57896044618658097711785492504343953926464851149359812787997104700240680714241
Ne sont-ce pas là des gros entiers ?
Puisque les 5 premiers nombres de Fermat sont premiers, Pierre de Fermat a conjecturé que tous les nombres de Fermat le sont. Un siècle plus tard, Leonhard Euler prouvait (avec l’algorithme exposé ci-dessous) que le 6e nombre de Fermat est divisible par 641, donc composé. Aujourd’hui on n’a pas trouvé de nombre de Fermat premier au-delà des 5 plus petits d’entre eux, et les tests de primalité sont difficiles à appliquer parce que les nombres de Fermat sont grands et il faut beaucoup de place en mémoire pour les stocker.
Mais le test de primalité isProbablePrime des gros entiers répond très vite pour des nombres de Fermat comme les précédents, qui sont gros sans être trop gros :

La réponse (false) vient très vite, ce qui veut dire que le 7e nombre de Fermat possède des diviseurs premiers. Comment les trouver en un temps raisonnable ? La théorie d’Euler fournit un algorithme assez rapide :
Si le nombre de Fermat $F_n=2^{2^n}+1$ possède un diviseur, celui-ci est nécessairement congru à 1 modulo $2^{n+2}$.
Par exemple, le célèbre diviseur 641 de $F_5$ est bien congru à 1 modulo 128.
Il suffit alors de chercher exclusivement des diviseurs du nombre de Fermat qui vérifient la condition ci-dessus ; ces diviseurs potentiels sont en progression arithmétique de raison assez grande, et en effectuant les divisions, l’algorithme suivant converge relativement vite :
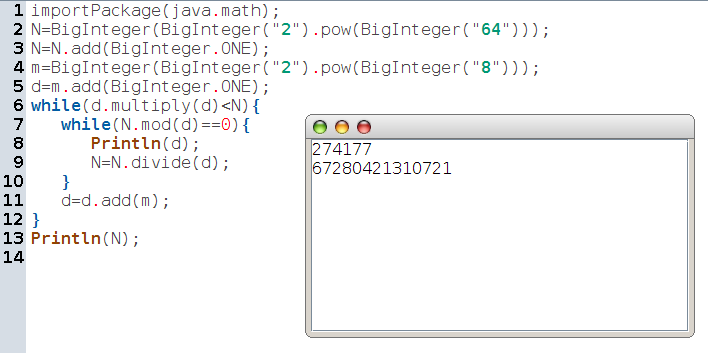
La fenêtre de sortie, affichée par-dessus le script, donne la décomposition en facteurs premiers du 7e nombre de Fermat.
Évidemment un logiciel de calcul formel donne lui aussi, et assez rapidement, la réponse (ici giac-Xcas, sous TeXMacs) :

L’approche algorithmique est différente, ne serait-ce que du point de vue didactique (la joie de la création...).
Multiprécision
L’import de la bibliothèque math de Java ne donne pas seulement accès aux gros entiers, mais également aux gros décimaux (BigDecimal). Le mode de fonctionnement est le même que dans les onglets précédents :
Pour créer un nombre en multiprécision, l’écrire comme une chaîne de caractères, et fournir celle-ci à BigDecimal : Par exemple, pour convertir 1,2 en gros décimal, on peut simplement faire ceci :
importPackage(java.math);
a=BigDecimal(1.2);
Println(a);Problème : On a ceci :
1.1999999999999999555910790149937383830547332763671875
Ce qui explique certains problèmes avec les fractions...
Pour éviter cela, il faut surtout éviter de passer par la valeur binaire de 1,2 et donc mettre 1,2 entre guillemets :
importPackage(java.math);
a=BigDecimal("1.2");
Println(a);Une alternative est de calculer le quotient comme un quotient de gros décimaux :
importPackage(java.math);
a=BigDecimal(BigDecimal(6).divide(BigDecimal(5)));
Println(a);Le nombre décimal écrit en chaîne de caractères peut aussi être donné sous forme d’écriture scientifique, comme 12E-1. On peut aussi fournir à BigDecimal un nombre entier, voire un gros entier. Et BigDecimal.ONE est le nombre 1 vu comme un gros décimal.
– Pour avoir l’opposé d’un gros décimal a, on fait a.negate() ;
– Pour additionner deux gros décimaux a et b , on fait a.add(b) ;
– Pour soustraire deux gros décimaux a et b , on fait a.subtract(b) ;
– Pour multiplier deux gros décimaux a et b , on fait a.multiply(b) ;
– La puissance de a s’obtient par a.pow(n) ;
Pour la division, c’est plus compliqué parce qu’il faut indiquer le nombre de chiffres à garder dans le quotient, ainsi que la manière d’arrondir le dernier chiffre (un entier parmi BigDecimal.ROUND_DOWN, BigDecimal.ROUND_UP, et 5 variantes visibles dans la référence ).
Par exemple, pour afficher 100 décimales du quotient de 22 par 7, arrondies par excès, on peut faire
Le reste euclidien d’un gros décimal a par un gros décimal b s’obtient par a.remainder(b).
Racines carrées
C’est maintenant que ça commence à devenir franchement algorithmique : Les gros décimaux n’ont pas de fonctions trigonométriques, exponentielles, racine carrée... Donc si on a besoin de connaître la racine carrée de 2 à 1000 décimales, on doit d’abord trouver un moyen de calculer la racine carrée ! Pour sa célébrité et sa rapidité de convergence, on va prendre la méthode de Héron. Et là déjà, se pose un problème inattendu : Jusqu’où doit-on aller pour être sûr d’avoir 1000 décimales correctes ? En tablant sur un doublement du nombre de décimales à chaque itération, on peut obtenir une borne supérieure au nombre nécessaire d’itérations, mais on peut aussi essayer expérimentalement, en affichant la différence entre les deux bornes données par l’algorithme de Heron, et en adaptant le nombre de boucles jusqu’à ce que la différence affichée soit inférieure à la millième décimale ; on trouve alors 11 pas :
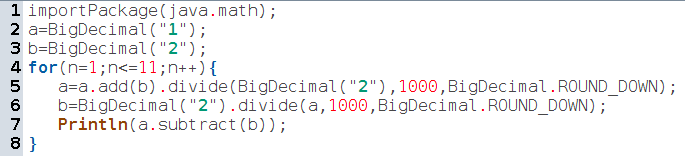
Ci-dessus on a encadré $\sqrt{2}$ entre deux suites $a_n$ et $b_n$ telles que $a_0=1$, $b_n=\frac{2}{a_n}$ et $a_{n+1}=\frac{a_n+b_n}{2}$. On s’est arrêté lorsque $a_n-b_n$ est suffisamment petit, en relançant l’algorithme jusqu’à ce que l’affichage final soit assez petit : 11 itérations ont donc été nécessaires.
Maintenant, on a un moyen de calculer la racine carrée de 2 à 1000 décimales par défaut, simplement en affichant la valeur finale de a [4] :
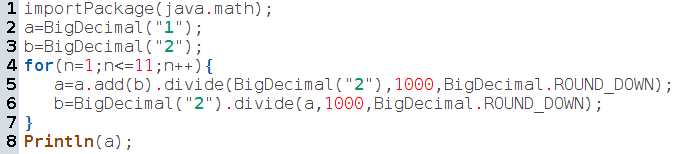
Maintenant qu’on a 1000 chiffres, il peut être intéressant de faire une étude statistique dessus. Pour cela un moyen rapide avec JavaScript est l’utilisation d’une expression régulière, fabriquée avec la recette suivante :
- on convertit le chiffre dont on veut compter les occurences en caractère (on le met entre guillemets) ;
- on « compile » le caractère « g » qui va rendre la recherche globale (on ne cherche pas le premier « 7 », on cherche tous les « 7 ») ;
- on lance la RegExp, telle un chien de chasse, à la recherche des occurences du chiffre ;
- On obtient alors une longue liste de chiffres tous identiques (que des « 7 » par exemple) ; on calcule alors la longueur de cette liste pour avoir l’effectif correspondant.
Le script obtenu est le suivant :
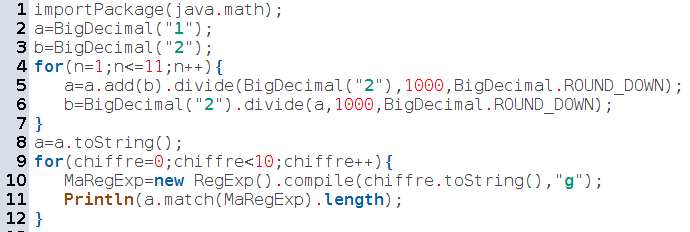
Et le tableau des effectifs obtenu :
| chiffres | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| effectifs | 108 | 99 | 109 | 82 | 100 | 104 | 90 | 104 | 113 | 92 |
La répartition est suffisamment uniforme pour donner l’impression que la racine carrée de 2 est un nombre normal en base 10.
Exponentielle de l’unité
Le nombre e ne fait pas un bon titre avec sa seule lettre (Georges Perec n’apprécierait guère), alors autant le décrire comme l’image de 1 (qui est ici un gros décimal) par la fonction exponentielle. Pour calculer rapidement e à 1000 décimales, on peut utiliser sa série entière, tronquée au rang ... Tiens mais au fait, au rang combien ? Jusqu’où doit-on aller pour que l’inverse d’une factorielle soit plus petite que la millième décimale ? Jusqu’où doit-on aller pour que la factorielle d’un nombre soit supérieure à $10^{1000}$ ?
On peut répondre à la question avec la formule de Stirling, ou tout simplement par tâtonnements :

Bingo ! Il faut donc boucler 450 fois (ou additionner 450 termes) ; bien que ce ne soit pas très prudent, on va tronquer systématiquement chaque terme, ce qui risque de fausser les 3 dernières décimales affichées.
Pour calculer les factorielles, on va les stocker dans une variable p (comme « produit ») qui sera initialisée à 1, mais vu comme un gros décimal. et on va additionner à la variable s (comme « somme ») les inverses des valeurs successives de p, obtenues en divisant le gros décimal 1 par p :
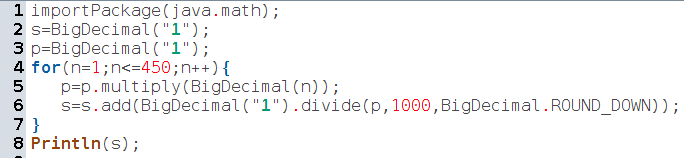
Pour en savoir plus sur les gros décimaux, voir la référence ; la comparaison avec la version Python est également intéressante.
Complexes
Cependant, les concepteurs de Java ont oublié les nombres complexes. La raison profonde de ce fait est la propriété archimédienne de l’ensemble des réels, ou plus exactement le fait que celui-ci soit ordonné. En effet en Java les nombres (qu’ils soient entiers, réels, gros entiers ou gros décimaux) sont des cas particuliers de tous les objets qu’on peut ordonner, comme les dates et les chaînes de caractères :
Et bien entendu les nombres complexes ne sont pas comparables entre eux : Pour un langage objet comme Java, les complexes ne sont pas des nombres ! Et donc ils ne sont pas implémentés.
Mais pour gérer les intersections de coniques, le concepteur de CaRMetal avait besoin des complexes. Alors, très logiquement, il les a créés ! Donc, pour pouvoir effectuer des calculs sur des complexes (ou leur appliquer des algorithmes), on ne va pas importer un paquet du langage Java, mais directement un paquet du code source de CaRMetal, avec
importPackage(Packages.rene.zirkel.structures)Une fois que c’est fait, il suffit d’entrer z=Complex(3,2) pour avoir le nombre complexe 3+2i dans le CaRScript. Cependant cet objet est encore un peu abstrait, et ne s’affiche pas comme on le voudrait :

En gros, on apprend que z est un complexe et on voit l’adresse mémoire de z (elle change à chaque exécution). Pour afficher le contenu de z, on peut demander séparément ses parties réelle et imaginaire en faisant suivre le nom z d’un point puis de real() pour la partie réelle ou img() pour la partie imaginaire [5] :

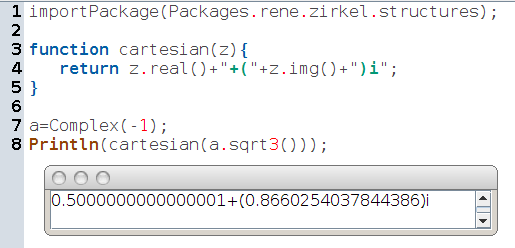
Comme on aura souvent à afficher des nombres complexes dans la suite, il est plus commode de créer un algorithme d’affichage plutôt que recommencer ce qui est fait ci-dessus ; ce qui en JavaScript se fait avec une « fonction » appelée cartesian (ce choix sera expliqué ci-dessous) :

Pourquoi cartesian ? Parce qu’un nombre complexe peut aussi être déterminé par sa forme trigonométrique, ci-dessous nommée polar [6] :
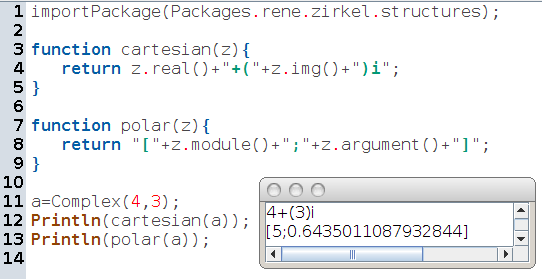
On voit ci-dessus (avec l’affichage produit) que la forme cartésienne de 4+3i est plus facile à lire que sa forme trigonométrique, et que les angles sont donnés en radians à 16 décimales.
De toute manière, les noms cartesian et polar sont des choix personnels réalisés en JavaScript, qu’on peut donc facilement changer. De même, si on n’aime pas la syntaxe z.img(), on peut la changer en écrivant quelque chose comme
function imaginaire(z){
return z.img();
}Opérations
L’objet complexe de CaRMetal ne possède pas d’opérations unaires comme l’opposé, l’inverse ou le conjugué. Les créer comme des fonctions JavaScript est laissé en (excellent) exercice. On écrit
- a.plus(b) pour additionner deux complexes a et b ;
- a.minus(b) pour les soustraire ;
- a.mult(b) pour les multiplier ;
- a.divide(b) pour les diviser ;
- a.sqrt() pour avoir l’une des trois racines carrées de a
- et a.sqrt3() pour avoir l’une de ses trois racines cubiques.
On peut aussi multiplier un complexe par un réel, par exemple calculer son double :

Certains complexes sont réels
Pour l’instant, CaRMetal ne sait pas qu’un complexe de partie imaginaire nulle est réel. Pour explorer numériquement le fait que la somme et le produit d’un complexe par son conjugué sont réels, on a donc besoin d’un test de réalité, et d’une conversion en réel. Comme on l’a vu précédemment, un complexe est réel si sa partie imaginaire est suffisamment petite, réclamer qu’elle soit sctrictement nulle est trop demander à JavaScript qui n’aime pas trop les nombres décimaux. Par ailleurs, si un nombre complexe est réel, il est facile de le convertir en nombre réel (il suffit de le transformer en sa partie réelle) mais que faire si l’utilisateur essaye de convertir en réel un nombre qui ne l’est pas ? Ici on choisit de renvoyer un discret message d’erreur plutôt que de tout bloquer, en disant que la conversion a abouti mais que son résultat n’est pas un nombre réel :
Exploration d’une transformation
Pour finir, un CaRAScript permet de construire un nombre complexe dynamique, en choisissant comme parties réelle et imaginaire de celui-ci, les coordonnées du point qui appelle le CaRAScript, ci-dessous notées X(« $name$ ») et Y(« $name$ »). On va s’en servir pour explorer dynamiquement la transformation $z \mapsto \frac{1}{\bar{z}}$. Cette activité peut être motivée purement algébriquement par la constatation que l’inverse et le conjugué d’un complexe non nul ont tous les deux le même argument, et donc que $Arg\left(\frac{1}{\bar{z}}\right)=Arg(z)$.
Dans le script ci-dessous, on note z le nombre complexe, et Z son image par la transformation. Un point également nommé Z doit être présent dans la figure avant de lancer le script, et il est assujetti par le script à rester l’image du point initial :

Pour que ce script fonctionne, il faut, par le gestionnaire de scripts, l’associer aux mouvements d’un point autre que Z (voir le TP 51 de l’onglet suivant pour voir comment on fait ça). Alors lors des mouvements de ce point, on voit
- que les deux points restent alignés avec l’origine (remarque sur les arguments ci-dessus) ;
- que la transformation a une infinité de points fixes ;
- que ceux-ci sont disposés sur une courbe remarquable ;
- que la transfomation est involutive...
Cerise sur le gâteau : CaRMetal possède un outil « inversion » avec lequel il est bon de comparer la transformation explorée...
TP Complexes
Résolution des équations du second degré
Au programme de Terminale S, ne figurent que les équations à coefficients réels, mais il sera plus simple de les convertir automatiquement en complexes, et de tout faire dans le champ complexe.
Tout d’abord, on peut vérifier que vu comme un complexe, -1 possède une racine carrée :
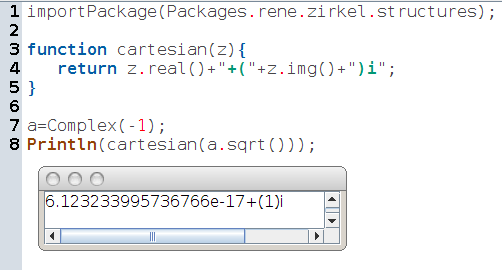
En estimant que la partie réelle est nulle aux erreurs d’approximation près, on réalise que la racine carrée en question est i.
L’algorithme de résolution des équations du second degré est plus simple dans sa version complexe que dans sa version réelle parce qu’il n’y a plus besoin de test. Ci-dessous, d1 est l’une des racines du discriminant et d2 l’autre racine. Comme CaRMetal n’a pas d’opposé des nombres complexes, on multiplie d1 par -1 pour avoir d2. x1 et x2 sont alors les deux solutions de l’équation, et la fonction trinome retourne un tableau contenant leurs écritures cartésiennes :
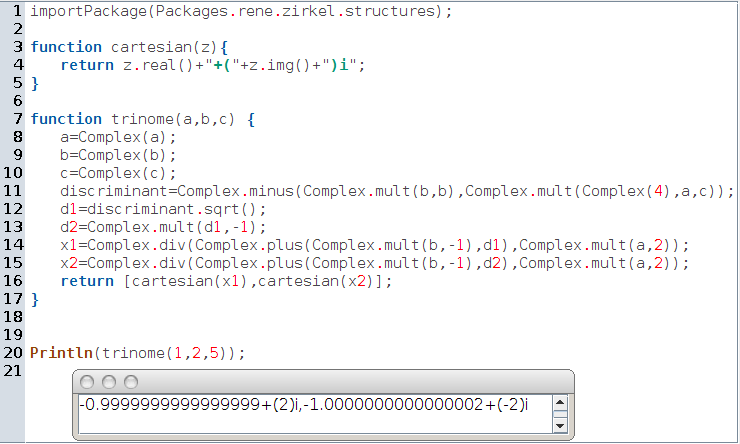
On voit que les solutions de l’équation $z^2+2z+5=0$ sont $-1+2i$ et $-1-2i$, mais comme précédemment il faut un peu d’entraînement pour reconnaître la partie réelle des deux solutions !
On aborde maintenant des sujets de l’épreuve expérimentale du bac S 2009 :
Sujet 051
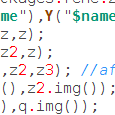
Celui-là est un très bon prétexte à un CaRAScript : Sur une figure CaRMetal comprenant le point O(0,0), le cercle de centre O et de rayon 1, un point M sur le cercle, et deux points N et Q libres dans le plan, on peut utiliser l’algorithme suivant :
- récupérer l’affixe z de M ;
- calculer son carré z2 et son cube z3 ;
- les additionner (on remarque que la somme de plus que deux termes est parfaitement gérée par CaRMetal) ;
- déplacer les points d’affixes respectifs z2 et q (la somme).
En JavaScript ça donne ceci :

Pour finir, il reste à ouvrir le gestionnaire de scripts pour associer à ce script, le point M :

Après cela, tout mouvement de M va faire bouger N et Q, permettant ainsi de conjecturer l’alignement considéré.
Sujet 111
Puisqu’on itère une fonction f, un bon début est d’implémenter celle-ci en JavaScript :

Sujet 112
Bien que prévu pour un logiciel de calcul formel, ce TP se prête bien à un traitement algorithmique avec CaRMetal, à condition d’utiliser un tableau de complexes :
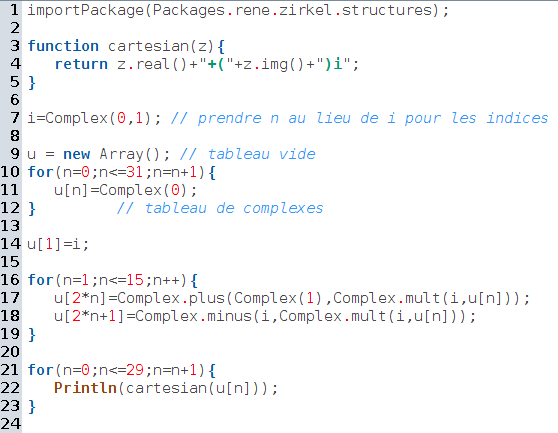
La suite du TP est laissée en (intéressant) exercice, vu qu’il est presque aussi aisé d’additionner les termes d’un tableau lorsque ceux-ci sont complexes que lorsqu’ils sont réels (par contre, trier les éléments du tableau est beaucoup plus difficile dans ce cas !).




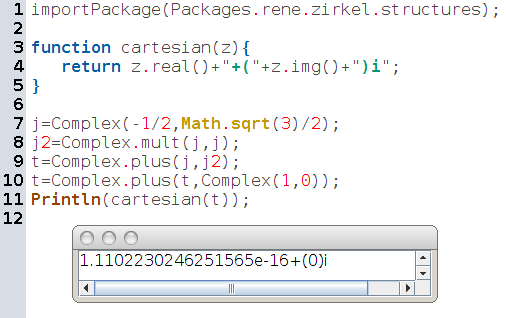
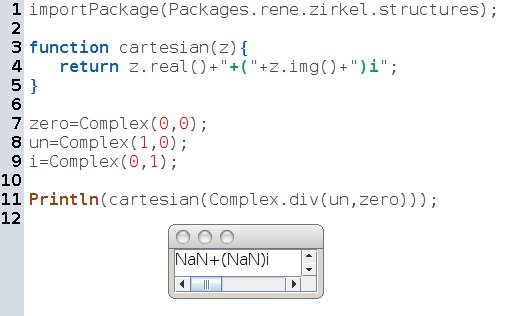



Commentaires