1 2 3 4 5

Dans le célèbre syllogisme « Socrate est un homme », la seconde proposition « Tout homme est mortel » est

• une implication ($x$ est un homme $\Rightarrow$ $x$ est mortel)
• mais aussi une inclusion (de l’ensemble des hommes dans l’ensemble des êtres mortels).

Cette double interprétation était utilisée par Leonhard Euler dans "Lettres à une princesse Allemande" par le diagramme suivant :

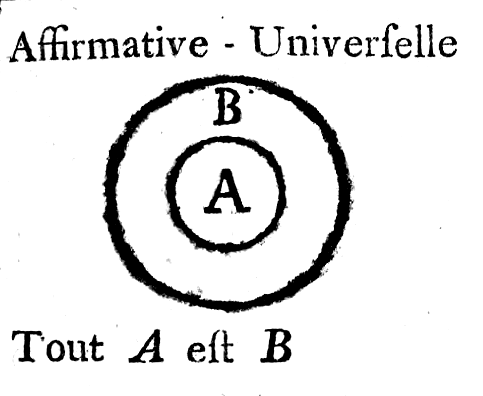
Des cercles ! Justement, en géométrie, on étudie des cercles : Peuvent-ils servir à illustrer les opérations booléennes de conjonction, disjonction, avec un outil de géométrie ?

Plan

Intersection et réunion avec CaRMetal

Le lien entre "et" et $\cap$ n’est pas seulement important en probabilités mais aussi en logique. Pour ne pas parler de $\forall$ et consorts, il suffit de bouger un point $M$ et de regarder ce qui se passe s’il est à l’intérieur d’un cercle ou d’un autre (ou des deux) :

Comment ça marche ? Le texte "$M \in A$" devient invisible lorsque $M$ est à l’extérieur de A (qui est un cercle) ce qui s’obtient en mettant dans l’onglet "conditionnel" du texte, à la propriété "invisible",

!inside(M;A)

Le point d’exclamation code une négation, sous CaRMetal comme dans JavaScript (entre beaucoup d’autres). On peut lire ceci par "le texte est invisible sauf si M est à l’intérieur de A". Pour le texte concernant B c’est le même principe. Mais pour l’intersection ? Et bien pour que M soit dans $A \cap B$ il faut et il suffit que M soit à la fois dans A et dans B, ce qui se code

!(inside(M;A)&&inside(M;B))

Après la négation, on trouve la conjonction, codée par "&&" : M doit être à la fois dans A et dans B pour être dans leur intersection. Et pour la réunion, il suffit de remplacer "et" par "ou" (un trait vertical dédoublé) dans une formule analogue. Il est vivement conseillé de télécharger la figure en cliquant-droit sur le lien au bas de cet article, et de l’ouvrir avec CaRMetal pour "voir comment c’est fait".

On peut illustrer ce premier diagramme de Venn par une situation probabiliste : On tire une carte d’un jeu de 32 ; quelle est la probabilité qu’elle soit un trèfle ou une figure ?" Ici les trèfles peuvent être représentés par A (8 cartes) et les figures par B (12 cartes). La question revient à compter les cartes qui sont bleues (les trèfles) ou rouges (les figures). Il est plus simple de compter celles qui sont les deux à la fois (elles apparaissent en mauve à cause de la composition des couleurs) : On en trouve 3, à savoir $A \cap B=\left\{Valet\clubsuit ;Dame\clubsuit ;Roi\clubsuit\right\}$

Récapitulation pour ce premier onglet

Qu’avons-nous établi avec ce diagramme de Venn ?

1. On a montré que $\cap$ veut dire "et" et que $\cup$ veut dire "ou".
2. On a montré qu’en JavaScript, mais aussi dans CaRMetal, "et" se note "&&" et "ou" se note "||"
3. On a révisé les aires de disques (pas inutile en Seconde)
4. On voit que si $A \cap B=\emptyset$, $P(A\cup B)=P(A)+P(B)$ (l’aire totale est la somme des aires). Ce qui amène rapidement à la définition des probabilités telle qu’elle figure dans le programme de Seconde.
5. bien que ce ne soit pas au programme, on peut assez facilement montrer les lois de DeMorgan (par exemple $\overline{A \cup B}=\overline{A}\cap\overline{B}$ : le contraire de "fromage ou dessert" c’est "ni l’un ni l’autre"). Et on les illustre avec les tests sous CaRMetal !
6. En vue de la fin du chapitre sur les probabilités, la vision du diagramme de Venn lorsque $A \cap B \neq \emptyset$ montre immédiatement par addition des aires que $P(A \cup B)=P(A)+P(A \cap B)+P(B)$.
   

1 2 3 4 5