Les plus anciens des lecteurs - s’il y en a - peuvent se souvenir du Petit Archimède, revue des années 70-80 où l’on faisait, entre autre, de l’algorithmique avant que nous ayons des ordinateurs personnels. C’était donc de l’informatique débranchée avant l’heure, avant même l’informatique au collège. Dans le numéro 14 (PDF), de 1975, on présente les polygones ainsi :
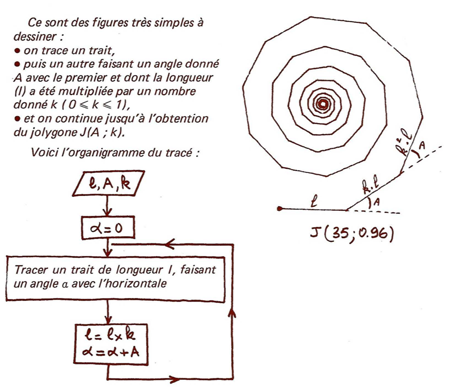
Nous allons nous amuser à chercher des cas particuliers intéressants. Cela n’aura pas d’utilisation directe en classe (à part les jolygones de base), mais éventuellement en formation des enseignants pour illustrer la possibilité de se poser de nouvelles questions quand la géométrie dynamique rencontre le codage.
Le travail que nous proposons sur les nombres complexes et l’analyse pourrait avoir une utilisation en lycée, si les nombres complexes, dans leur rapport à la géométrie, reviennent dans les programmes. Ce n’est pas impossible car la trace d’une tortue est naturellement une somme de nombres complexes et cela permet une étude intéressante comme nous allons à nouveau le montrer ici.
La dernière partie de cet article est plus technique, et n’intéressera pas tous les lecteurs. Cette figure va en effet être l’occasion de détailler l’insertion des cases à cocher et des pop up dans DGPad, fonctionnalité présente depuis longtemps mais finalement peu documentée.
Bien entendu, tout ce qui est proposé ici serait réalisable avec les séquences de GeoGebra. On a choisi ici d’illustrer une nouvelle fois la rencontre entre la géométrie et le codage « par bloc » comme le propose DGPad.
1. Un peu de code ... et de géométrie
En appliquant l’organigramme précédent, avec la programmation par bloc, en utilisant deux curseurs (celui sur la longueur n’est qu’un zoom), on peut écrire tout simplement :

Figure à manipuler dans l’article (et présentation avec les complexes)
Explorations
On peut faire observer aux élèves que si l’angle est un diviseur de 360, les côtés du jolygone sont parallèles : tester 60 ou 72°, mais aussi, faire tester 80° par exemple, diviseur de 720°, soit deux tours.
Dans l’esprit de la suite, observer - même si l’angle se modifie par demi degré - qu’avec le coefficient de l’ouverture de la figure, les angles 62,5° et 70° rendent le jolygone tangent à lui-même au sens où chaque sommet appartient à un segment antérieur (approximativement car les angles ne sont pas continus). Il y a donc deux angles pour même sommet, pour un coefficient donné.
De même pour un angle quelconque, observer que l’on peut choisir un coefficient k pour que le jolygone devienne « auto-tangent ».
Similitude associée au jolygone
C’est ce que nous allons étudier dans la suite. Avant cela, regardons, pour la culture, un exercice classique des Terminales C et E sur les similitudes quand ces sections existaient. En effet les jolygones étaient alors un exercice archétypique sur la recherche du centre d’une similitude directe. En effet, pour un coefficient inférieur à 1, on voit que la trace de la tortue converge vers un point ... c’est le centre d’une similitude associée au jolygone.
Dans la figure suivante, on recouvre la trace de la tortue par une liste de segments construite avec Blockly - ie sans le module tortue - directement par l’application itérée de la similitude de centre O, de rapport k, et d’angle a, comme on le voit dans le code suivant :
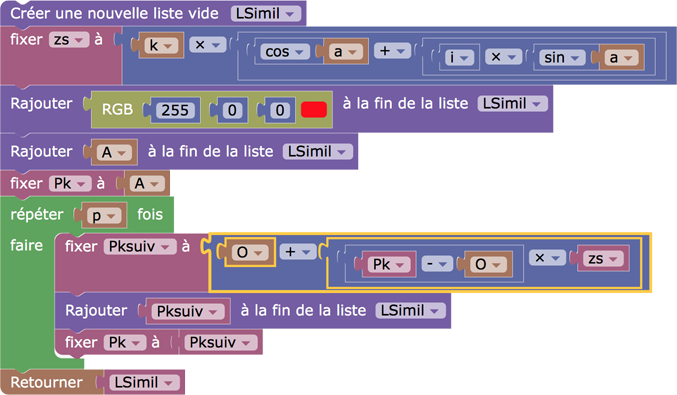
Figure de recouvrement par similitude (en manipulation directe dans l’article)
Deux remarques techniques :
Pour 4 itérations il y a 6 éléments dans la liste car il y a d’abord la couleur, puis le point A (p=0, puis les 4 autres points associés aux 4 affixes suivants.
Pour construire le point O, il faut transformer l’unité de la tortue, le pixel en, celle de DGPad. Cela se fait simplement en divisant la valeur de la variable long par le nombre de pixels en une unité, en utilisant l’expression pixel(), collée à la variable, dans une formule. L’affixe du O s’exprime alors ainsi :
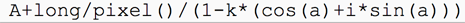
On aurait pu utiliser Blockly pour cette expression, mais c’est l’occasion de montrer cette possibilité.
2. Les jolygones contraints : un peu d’analyse
Toujours dans le même repère construit sur le premier segment, l’extrémité de la trace de la tortue, à la $(p-1)^{i\grave{e}me}$ itération est le point d’affixe $z_p = \displaystyle \sum_{q=0}^{p-1} k^qe^{iqa}$ s’écrit aussi $\displaystyle \frac{1-k^pe^{ipa}}{1-ke^{ia}}$.
Ce point sera sur le premier segment du jolygone si et seulement si l’affixe de $z_p$ est un nombre réel, soit, en multipliant par le conjugué du dénominateur, ssi, après simplification :
$sin(a) +k^p sin((p-1)a) - k^{p-1} sin(pa) = 0$
2.1. $k$ contraint à angle donné
Ainsi, pour un angle $a$ donné, on peut cherché $k<1$ solution de cette équation, et pour $k$ donné, on peut chercher une solution $a$, pour différentes valeurs $p$ qui correspond au segment dont on cherche le contact de l’extrémité avec le premier segment du jolygone.
A priori on cherche le premier segment qui permet ce contact (on évite d’avoir un segment qui coupe et le suivant qui serait "tangent"). La valeur de $p$ est alors facile à construire. La recherche de $k$ peut alors se faire par simple dichotomie. Voici le code standard (pour la fonction, on utilise des variables locales juste pour que l’affichage reste lisible dans l’interface du site).

Remarque : l’utilisation d’un "Tant que" dans une interface qui réagit en temps réel peut poser problème. On reviendra dessus en détail dans la partie d’explication technique. L’idée principale est de remplir ce bloc en le laissant déactivé.
Dans la figure suivante, on choisi ensuite de ne mettre en oeuvre ce coefficient - quand il existe (cas de segments non parallèles) que pour une valeur $k>0,9$. Voici une copie d’écran de la figure avec le jolygone réalisé pour le $k$ du curseur, et, à droite, quand on choisi (case à cocher) la valeur de $k$, affichée, pour que le jolygone soit "auto-tangent".

Explorer la figure en ligne (pour éviter de trop surcharger l’article)
Sur cette figure, on peut conserver la case de $k$ contraint cochée, et modifier l’angle. Le jolygone se modifie en restant auto-tangent.
2.2. Angle contraint à $k$ donné - Présentation
Cette partie est plus intéressante car, pour un coefficient donné, on peut choisir le rang du segment qui va retoucher la première fois le segment de départ. On s’intéresse donc à la cherche d’un angle $\theta$ solution, pour $k$ et $p$ donnés de l’équation
$sin(\theta) +k^p sin((p-1)\theta) - k^{p-1} sin(p \theta) = 0$
Regardons le tracé de la fonction associée, pour un angle en degré. Explorer cette figure Desmos manipulable en ligne. En voici quelques copies d’écran.
Tout d’abord trois valeurs de $p$ pour la même valeur $k=0,973$. Quand il y a des solution, la première est - naturellement - aprés $360/p$, valeur qui correspondrait à ce que le point de contact soit en A.

Puis, pour une valeur de $k$ plus proche de 1 $(k=0,9916)$, on voit où il y a d’abord deux premières solutions, dans l’environnement de $360/p$ et deux autres solutions plus loin.

Mais ces deux autres valeurs ne correspondent pas à une première rencontre avec le segment initial comme on le voit ci-dessous : on présente les deux premiers angles solutions (p est arrondi à 3 décimales dans l’illustration) et la quatrième valeur autour de 102°.
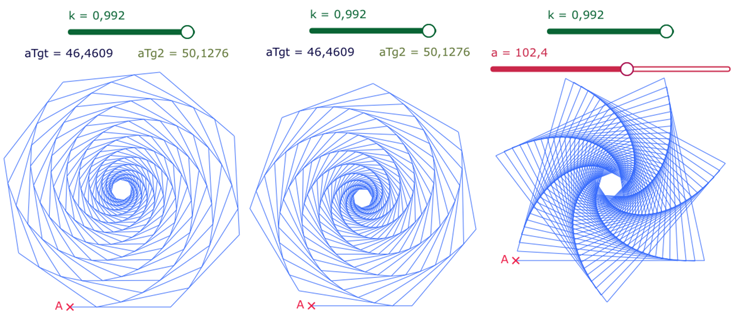
2.3. Angle contraint à $k$ donné - Exploration générique du bassin de convergence de la dichotomie
On aurait pu utiliser cette première exploration pour se donner des bornes de dichotomie efficaces, dans des listes par exemple. On a choisi ici de réaliser une programmation plus générale où l’on cherche soi-même des bornes effectives des bassins de convergence pour les deux premières solutions.
La différence par rapport au code précédent est que, pour le premier angle, on cherche la borne supérieure de l’intervalle dans lequel on va appliquer la dichotomie. Si on ne la trouve pas c’est qu’il n’y a pas de solution :

Alors que pour la cherche du second angle, on sait qu’il existe, si le premier existe. On effectue donc, pour la borne supérieure, une itération à partir de la premier solution. Les deux fonctions Choix de b et Choix2 de b sont quasi identiques avec une inégalité opposée sur la valeur de la fonction $g$. On aurait pu prendre la même fonction avec un paramètre.
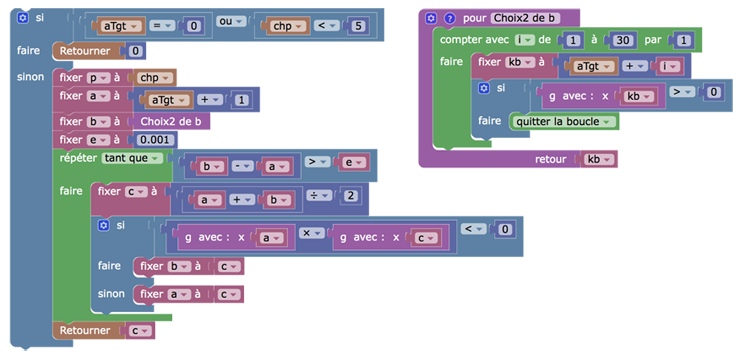
Voici une illustration de la figure finalisée pour le cas p=6
On aura remarqué que le second angle n’est pas calculé pour $p=4$. Pourtant en général il existe, mais assez loin de la première valeur. Dans la figure en ligne proposée ci-dessous, on peut vérifier cette exploration sur le second angle, ou modifier la fonction b2 du code pour qu’elle trouve cette seconde solution pour p=4
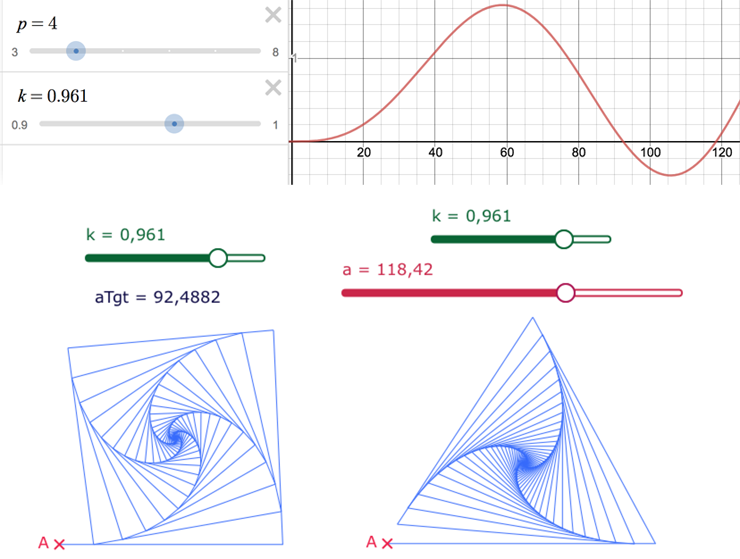
La figure DGPad
Manipuler la figure en ligne associée.
On peut donc choisir le type de contrainte dans un pop up menu (aucune, $k$, ou $a$) et pour la contrainte sur l’angle, choisir dans un autre pop up le paramètre $p$, et choisir enfin d’afficher la trace de la tortue pour la première ou la seconde solution de l’angle.
On a laissé les expressions $aTgt$ et $aTg2$ visible pour que les plus curieux des lecteurs puisse rentrer dans le code Blockly qui les calcule, et éventuellement le modifier.
Dans la partie suivante, on revient plus en détail sur la façon dont sont réalisés dans DGPad ces pop up menus et autres détails techniques autour de la gestion des booléens : le logiciel étant à l’origine réalisé pour tablette tout est un peu caché à l’intérieur de l’interface. Les figures sont téléchargeables en fin d’article.
3. La mise en œuvre technique dans DGPad
Cette partie est développée en trois parties :
– les pop up et cases à cocher dans les widgets
– détail de la gestion associée des booléens
– traitement spécifique du « Tant que ».
La partie widgets
1. Les balises div et span
Dans un widget, on peut mettre pratiquement tout ce que l’on veux (HTML et LaTeX). On commence en général par une balise div que l’on modifie, en général, par des balises span. Voici le texte du début du widget de la dernière figure :

A titre personnel, je n’ai jamais utilisé les 3 icones dema gauche. Je préfère avoir une bibliothèque de balises toutes prêtes (en mode texte) que je copie colle (pas avec Cmd-C / Cmd-V désactivés mais par clic droit sur ordinateur) dans le code du widget ... d’où souvent les mêmes couleurs par exemple dans mes figures.
2. Les pop-up et les cases à cocher
Ces deux outils sont liés à des expressions - pour la valeur du choix. Commencer par créer ces expressions (ch pour le choix de type de jolygone, et cha2 pour le choix du second angle dans la contrainte sur les angles. Ensuite le code est très simple, c’est du HTML. Voici les exemples pour cette même figure.

Attention : il faut changer d’outil du tableau de bord pour fermer un widget, et surtout ne pas utiliser la croix en haut à droite qui correspond à la suppression complète du widget.
Gestion directe des booléens
Le code associé à la trace de la tortue (code en A) entre la première figure - de base - et la quatrième figure - avec toutes les options des contraintes - ne varie que sur les deux variables associée au coefficient de réduction (de k à kc - pour k contraint) et pour l’angle de rotation de la tortue, de a à ac2 - pour angle contraint avec la seconde valeur possible) :

Expression booléenne de kc
On a noté kTgt, la valeur, calculée par dichotomie, du coefficient de réduction pour que le jolygone ait ses sommets sur des côtés antérieurs. Le code de l’expression de kTgt a été présentée dans la partie précédente.
Nous voyons ici comment exprimer la valeur kc en fonction des nombreuses contraintes retenues : le coefficient vaut la valeur k du curseur si le choix (du pop up) n’est pas le cas k contraint (non ch=1), d’où ch==0 || ch==2, ou s’il n’existe pas une valeur de k contrainte si ch=1, (|| kTgt==0) , et si l’angle est inférieur ou égal à 97° (|| a>97.5 car le curseur est réglé en pas demi entier). Et bien entendu, kc est égal à kTgt, dans le cas contraire, ce qui s’écrit :

Les expressions ac et ac2 selon les différents choix
On a d’abord une expression ac qui choisit entre l’angle a du curseur et la valeur contrainte aTgt qui correspond au choix de la première valeur de l’angle pour un angle contraint.
Puis dans l’expression ac2 - qui est utilisée dans la trace - on fait le bilan final entre la valeur renvoyée par ac qui prend la valeur a ou aTgt et la valeur aTg2 qui correspond au second angle possible pour le choix contraint de l’angle.
En pratique on peut donc écrire, respectivement pour ac et ac2 les expression logiques suivantes :

Utiliser le « Tant que » dans Blockly
Le fait que le code Blockly réagit en temps réel nécessite de prendre des précautions pour utiliser une boucle Tant que. Il y a deux façons de le faire sans difficulté.
1. En laissant le bloc Tant que actif
On peut utiliser le bloc actif en lui mettant une condition toujours fausse. Voici un exemple sur aTgt. On voit qu’il n’y a qu’un trait de tracé, et quand on place le bloc correct, le tracé se met à jour.
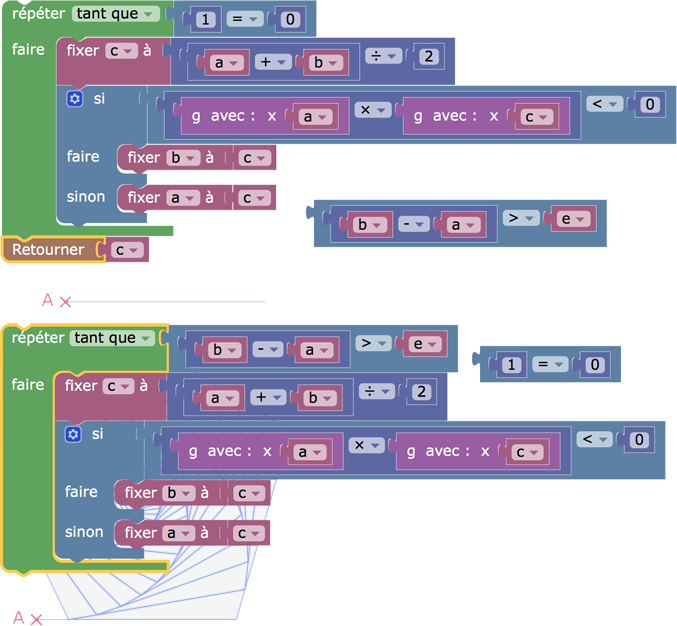
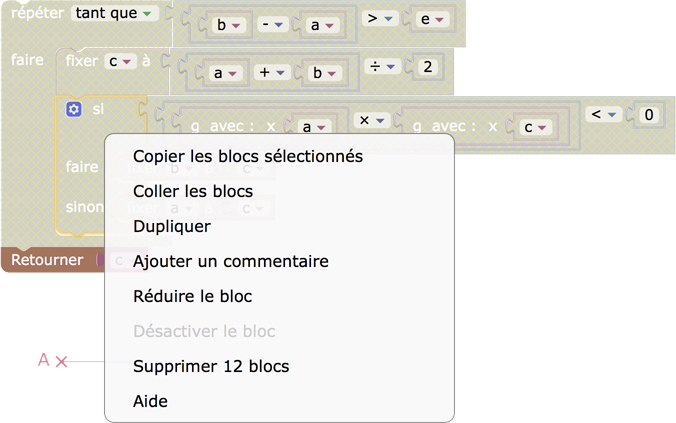
2. Ce qu’il ne faut surtout pas faire
Il ne faut surtout pas remplir la condition du Tant que pas à pas, par exemple en commençant par placer le bloc de comparaison et tenter de le remplir : cela bloque DGPad à coup sûr !
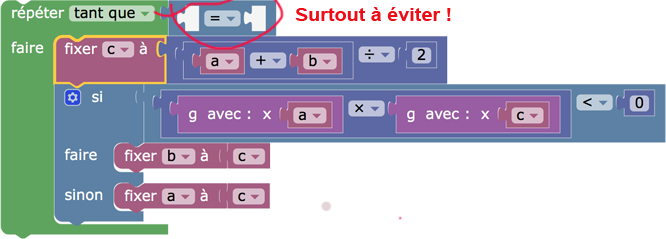
La démarche à retenir : comme dans la partie 1, on prépare à part un bloc logique toujours faux, que l’on place dans la condition, puis on prépare à côté la bonne expression que l’on glisse, une fois finalisée, à la place de la précédente.
3. Avec le bloc désactivé
C’est un peu moins confortable à travailler (pour la visibilité), mais garanti sans problème technique. Comme on le voit ici, on ne peux pas rendre « actifs » les blocs intérieurs au « tant que ».
4. Téléchargements associés
4.1. Le logiciel DGPad et autres travaux de Eric Hakenholz
Il s’utilise en webApp sur toute plateforme avec l’adresse (en https) : https://www.dgpad.net/index.php
Avec cette adresse, vous pouvez glisser les figures téléchargées (en .dgp sur Mac) directement sur la fenêtre. Le site du logiciel.
Présentation par l’auteur, Eric Hakenholz. Voir sa chaine youtube).
DGPad existe aussi pour iOS et Androïd que l’on trouve sur les sites de téléchargement de GooglePlay et App Store.
Le logiciel a aussi été développé en application native sous Mac OS et Linux
DGPad sous mac : http://docs.dgpad.net/downloads/macos/dgpad_install.dmg
DGPad sous Linux (distribution Débian) : http://goo.gl/jUbwPn
Le blog de Patrice Debrabant sur CarMetal et DGPad : carmetal.org pour des informations récentes.
Un nouveau site de Eric Hakenholz (mai 2018) en mode adaptatif (reponsive design) : matpad (sans le h) : https://sites.google.com/view/matpad d’utilisation de DGPad en collège, a priori sur tablette mais pas nécessairement.
Eric a aussi développé des outils de facilitation de récupérations automatiques de travaux d’élèves sur tableur, DGPad, Snap et, désormais, sur Scratch 3.0 : voir ses DocTools.
4.2. télécharger les figures de cet article
Décompresser le zip et glisser les figures sur la webApp par exemple.
4.3. Autres exemples d’utilisation des nombres complexes pour la trace de la tortue
Dans cet article on a utilisé que le jolygone retouchait un segment précédent si le nombre complexe représentant l’extrémité de la trace de la tortue avait une partie imaginaire nulle.
Le changement de cadre de la trace de la tortue en somme de nombres complexes est particulièrement riche. Il peut être utilisé pour des preuves - et des développements plus fins - comme dans cet exercice initial de 5° sous Scratch.
Il peut surtout être utilisé pour réaliser des constructions dynamiques complexes comme dans le cas des spirolatères dynamiques . Voir la barre d’onglets 4 de cet article.
.


Commentaires