1. UNE APPROCHE NAÏVE DU LANGAGE MATHÉMATIQUE
1.1. Considérations syntaxiques
1.1.1. Langage mathématique et langage naturel
1.1.2. Expressions mathématiques
Les expressions mathématiques sont soit des noms, soit des énoncés ou propositions.
- Exemples de noms :
- $\int_0^1 x\,dx$
- $\lbrace x\in \textbf{R} /x^2+1=0 \rbrace$
- $\frac{1}{2}$
- Exemples de propositions :
- $x^2+1=0$
- Tout entier pair $\geq3$ est la somme de deux nombres premiers.
- $\lim_{x\rightarrow +\infty}\frac{3x-7}{2x^2+4}=\frac{3}{2}$
1.1.3. La notion de variable
C’est la notion de variable qui fait la différence entre le langage naturel et le langage mathématique.
On fait une utilisation massive de variables muettes.
1.1.4. Variables libres/variables liées - Mutifications
- Exemples :
- Lorsque l’on dit : "L’équation en x : $ax^2-7x+1=0$ a au moins une racine réelle", x est une variable muette et a est une variable parlante.
- Dans l’équation $\cos^2x+\sin^2x=1$, x est une variable parlante.
- Dans l’équation $\left[ \forall x \in \textbf{R}\quad \cos^2x+\sin^2x=1 \right]$, x est une variable muette.
Dans une expression, une variable peut être muette (liée) ou parlante (libre). Lorsqu’une variable est muette, il y a "quelque chose" qui l’a rendue muette, comme, par exemple : $\int d\,\sqcup$, $\lbrace \sqcup /\dots{} \rbrace$, "l’équation"... Ce sont des mutificateurs. Un mutificateur est quelque chose qui rend muet (mutifier = rendre muet).
- Exemples :
- Dans la phrase "$x^2+1=0$ n’a pas de racine réelle", x est une variable muette car le mot "équation’’ est implicite.
- "$\cos^2x+\sin^2x=1$" et "$\textrm{cotan}^2x+\tan^2x=1$" n’ont pas d’implicite : x est donc une variable libre.
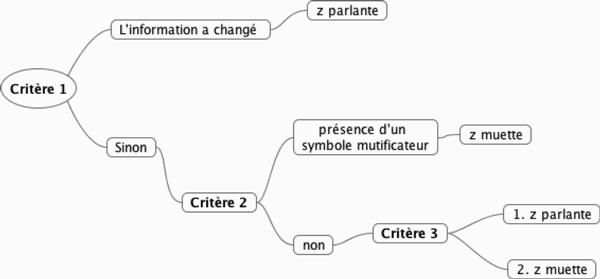
Trois critères pour savoir si une variable est muette ou parlante :
Critère 1 : Si je change x par y ou par u ou par z et que la nature de l’information a changé, alors c’est nécessairement une variable parlante.
- Exemples :
- Dans "$x \in \lbrace x\in \textbf{R} /\,{x}^2+1=0 \rbrace$", le premier x est une variable parlante et le second x est une variable muette. Si l’on renomme la variable muette, cela donne ici : $x \in \lbrace u\in \textbf{R} /u^2+1=0 \rbrace$. Le renommage ne concerne que les occurrences muettes de la variable.
- Dans "x peut se mettre sous la forme au+bv, avec u et v dans Z", le mot "avec" sous-entend un $\exists$ implicite (il masque une quantification existentielle).
- "$\cos^2x+\sin^2x=1$" est une expression à bannir, mais elle peut se rencontrer.
Critère 2 : Présence de symboles mutificateurs (qui rendent la variable muette i.e. liée).
- Exemples : $\int \, d\sqcup$, $\lbrace \sqcup / \dots{} \rbrace $, "l’équation en", $\forall \, \sqcup$, $\longmapsto $,
$ \sum_{\sqcup}$, $\prod_{\sqcup}$, $\exists\, \sqcup$, $\textrm{Sup}\,\sqcup$, $\textrm{Max}\, \sqcup$, $\textrm{Min} \, \sqcup$.
Critère 3 : Si je remplace les occurrences d’une variable z dans une expression E par un nom qui n’est pas une variable, deux choses peuvent se produire :
- Si le résultat de la substitution est encore une expression mathématique qui a un sens, alors la variable que l’on a remplacée était parlante.
- Sinon, la variable était muette.
- Exemples :
- $ \cos^2z+\sin^2z=1 \rightsquigarrow \cos^2\int_0^1 xdx+\sin^2\int_0^1 xdx=1$
- $\lim_{z\rightarrow +\infty}g(z)\leadsto \lim_{\int_0^1 xdx\rightarrow +\infty}g(\int_0^1 xdx)$
- Dans $\sum_{k=0}^{n} 2^k $, k est muette, n est parlante.
Résoudre un problème de maths, c’est souvent éliminer des mutifications.
1.1.5. Comment combiner des expressions pour en obtenir d’autres ?
$a>3$ est une phrase élémentaire. C’est ce que l’on appelle un énoncé atomique.
Les connecteurs permettent de fabriquer des propositions à partir de propositions données, idem pour les quantificateurs, par exemple :
$a>3 \Rightarrow \exists p \, \exists q \,( p \ \mathrm{est\ premier\ et} \, q \,\mathrm{est\ premier\ et\ } p+q=a)$
Liste des connecteurs
– Connecteurs binaires :
| et | ou | implique | équivaut à |
| $\wedge$ | $\vee$ | $\Rightarrow$ | $\Leftrightarrow$ |
– Connecteur unaire :
| non |
| $\neg$ |
Les quantificateurs
| universel | existentiel |
| $\forall$ | $\exists$ |
"$\forall x\, , \textrm{A}$" signifie : "pour tout x, A"
"$\exists x\, , \textrm{A}$" signifie : "il existe au moins un x tel que A", mais aussi : "pour au moins un x, A".
Conjecture de Goldbach :
$ \forall \, a \in \textbf{N} \, \left[ \left( a>3 \textrm{ et } a \textrm{ est pair } \right) \exists \, p \, \exists \, q \, \left( p \textrm{ est premier et } q \textrm{ est premier et } p+q=a \right) \right].$
Des mathématiciens chinois ont démontré que :
$ \forall \, a \in \textbf{N} \, \left[ \left( a>3 \textrm{ et } a \textrm{ est pair }\right) \exists \, p \, \exists \, q \, \exists \, r \, \left( p \textrm{ est premier et } q \textrm{ est premier et }\left( r \textrm{ est premier ou } r=1 \right) \textrm{ et } p+qr=a \right) \right].$
1.2. La signification des expressions
1.2.1. Valeurs de vérité. Tables de vérité des connecteurs
Si dans certaines conditions, on a attribué une valeur de vérité (Vrai ou Faux) aux propositions A et B, on peut dresser la table de vérité suivante :
| A | B | A et B conjonction |
A ou B disjonction |
A $\Leftrightarrow$ B équivalence |
A $\Rightarrow$ B implication |
| F | F | F | F | V | V |
| F | V | F | V | F | V |
| V | F | F | V | F | F |
| V | V | V | V | V | V |
- Exemples :
- $\textrm{A} \Rightarrow\textrm{B} \textrm{ avec A faux : } $
- $ \left[ \textrm{Pour tout } n \in \textbf{N} \left( n \textrm{ pair} \Rightarrow n^2 \textrm{ pair} \right) \right] $ est une proposition vraie.
- $ \left[ \textrm{Pour tout } n \in \textbf{N} \left( n \textrm{ pair} \Rightarrow 2n \textrm{ pair} \right) \right] $ est une proposition vraie.
- Choisir dans les deux cas $n=3$ pour obtenir A faux.
- $\textrm{A} \Rightarrow \left( \textrm{B} \Rightarrow \textrm{A} \right)$ est vraie tout le temps :
- Si A est faux, c’est vrai quelque soit B.
- Si A est vrai, $\textrm{B} \Rightarrow\textrm{A}$ est toujours vrai donc c’est vrai. C’est une tautologie.
- $\textrm{A} \Rightarrow\textrm{B} \textrm{ avec A faux : } $
Une tautologie est une proposition vraie quelques soient les valeurs de vérité attribuées aux propositions à partir desquelles elle est constituée (avec des connecteurs).
– Exemple de tautologie : $\left( \textrm{A} \Rightarrow \textrm{B} \right) \textrm{ ou } \left( \textrm{B} \Rightarrow \textrm{A} \right).$
1.2.2. Quelques règles pour le bon usage des connecteurs et des quantificateurs
On a des exemples de fonctions continues non positives ($x \mapsto -x^2$), donc on n’a pas :
$\forall \, f\quad f \, \textrm{continue}\Rightarrow f \, \textrm{positive}$.
On a des exemples de fonctions positives non continues ($x \mapsto 0\ \textrm{si}\ x<0, x \mapsto 1\ \textrm{si}\ x \geq 0$), donc on n’a pas :
$\forall \, f\quad f \, \textrm{positive}\Rightarrow f \, \textrm{continue}$.
Par suite, la phrase :
$ \left[ \forall f \quad f \textrm{ continue } \Rightarrow f \textrm{ positive} \right] \textrm{ ou } \left[ \forall f \quad f \textrm{ positive } \Rightarrow f \textrm{ continue} \right]$
est fausse.
Ce n’est pas pareil que :
$\forall f \quad \left[ (f \textrm{ continue } \Rightarrow f \textrm{ positive}) \textrm{ ou } (f \textrm{ positive } \Rightarrow f \textrm{ continue}) \right] $,
qui est une tautologie (phrase toujours vraie). Dans cette phrase-là, c’est le même f dans les deux arguments de la conjonction.
Un "$\forall$" ne se laisse pas distribuer sur un "ou".
Les propositions $\textrm{A}\Rightarrow\textrm{B}$, $\neg \textrm{A ou B}$ sont synonymes.
La proposition $\left( \textrm{A}\Rightarrow\textrm{B} \right) \vee \left( \textrm{B}\Rightarrow\textrm{C} \right)$ est une tautologie (faire une table de vérité avec 3 propositions, il y a donc 8 cas).
Écrivons que f est continue au point a :
$ \left( \forall \, \varepsilon \in \mathbb{R}_+^* \right) \left( \exists \, \eta_\varepsilon \in \mathbb{R}_+^* \right) \forall x \in \textrm{D}_f \left( \vert {x-a} \vert < \eta \Rightarrow \vert f(x)-f(a)\vert < \varepsilon \right) $.
Écrivons que f n’est pas continue au point a :
$ \left( \exists \, \varepsilon \in \mathbb{R}_+^* \right) \left( \forall \, \eta_\varepsilon \in \mathbb{R}_+^* \right) \exists x \in \textrm{D}_f \left( \vert {x-a} \vert < \eta \textrm{ et } \vert f(x)-f(a)\vert \geq \varepsilon \right) $.
$\textrm{non}\left( \textrm{A}\Rightarrow \textrm{B}\right)$ est synonyme de $ \textrm{A } \textrm{et } \neg\textrm{B}$
La négation d’une implication ne peut pas s’exprimer sous la forme d’une implication et il faut dire aux élèves que :
La négation d’une implication n’est pas une implication. C’est une conjonction.
Toutes les lettres sont astreintes à un certain référentiel :
$ \left( \forall \, x \in E \right) \quad A\left[ x\right] $
$ \left( \exists \, x \in E \right) \quad A\left[ x\right] $.
Voici les mêmes phrases avec des connecteurs :
$ \forall \, x \left( x \in E \, \Rightarrow \, A\left[ x\right] \right) $
$ \exists \, x \left( x \in E \ \textrm{et} \, A\left[ x\right] \right) $
$ \exists ! \, x \quad A\left[ x\right] $ s’écrit :
$ \exists \, x \left( A\left[ x\right] \wedge \forall y \left( y\neq x \Rightarrow \neg A \left[ y\right] \right) \right) $
Il existe au plus un $x$ tel que $A\left[ x\right] $ s’écrit :
$ \forall \, x \, \forall \, y \, \left[ \left( A\left[ x\right] \textrm{ et } A\left[ y\right] \right) \Rightarrow x=y \right] $.
1.2.3. Du bon usage des formules équivalentes
f injective se traduit par les deux phrases équivalentes suivantes :
$ \left[ \,\forall \, x \, \forall \, y \, \left[ f(x)=f(y) \Rightarrow x=y \right] \, \right] $ et
$ \left[ \,\forall \, x \, \forall \, y \, \left[ x\neq y \Rightarrow f(x) \neq f(y) \right] \,\right] $.
Quand un énoncé se termine par x = y, c’est un énoncé d’unicité.
L’équivalence logique ne signifie pas l’équivalence pédagogique. À dessiner, il vaut mieux dessiner la seconde
phrase.

$\textrm{A} \Leftrightarrow \textrm{B}$ est synonyme de $\textrm{B} \Leftrightarrow \textrm{A}$. Cela s’écrit : $\textrm{A} \Leftrightarrow \textrm{B} \sim \textrm{B} \Leftrightarrow \textrm{A}$.
Une table de vérité s’applique à des combinaisons booléennes de propositions. Faire une table de vérité de :
(1) $\boxed{ ab=0 \Leftrightarrow \left( a=0 \textrm{ ou } b=0 \right) }$
n’a donc aucun sens.
Par contre, celle de la phrase suivante a un sens :
(2) $\boxed{ \textrm{A} \Rightarrow \left( \textrm{ non B et C} \right)}$
(phrase dans laquelle A, B et C sont des variables propositionnelles).
Pour analyser la proposition (1), on fait des mathématiques (pas de la logique) et pour analyser la proposition (2), on fait de la logique.
$\textrm{A} \textrm{ et } \textrm{B } \sim \textrm{ B} \textrm{ et } \textrm{A}$
Écrire : "Les propositions $\textrm{A} \textrm{ et } \textrm{B }$ et $\textrm{ B} \textrm{ et } \textrm{A}$ sont équivalentes" pose un problème. Il vaut mieux alors écrire : "Les propositions $\textrm{A} \wedge \textrm{B}$ et $\textrm{B} \wedge \textrm{A}$ sont équivalentes".
$\left( \textrm{A} \Leftrightarrow \textrm{B}\right) \Leftrightarrow \left( \textrm{B} \Leftrightarrow \textrm{A} \right)$
Est-ce un nom ou un énoncé ? Il y a ambiguïté. Si l’on veut désigner un énoncé, on préfèrera alors écrire : $\textrm{A} \Leftrightarrow \textrm{B} \sim \textrm{B} \Leftrightarrow \textrm{A}$.
La proposition $\textrm{A} \Leftrightarrow \textrm{B} \Leftrightarrow \textrm{C}$ est-elle justifiée (c’est-à-dire sans parenthèse) ?
| A | B | C | $\textrm{A} \Leftrightarrow \textrm{B}$ | $\textrm{B} \Leftrightarrow \textrm{C}$ | $\textrm{A} \Leftrightarrow \left( \textrm{B} \Leftrightarrow \textrm{C}\right)$ | $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \Leftrightarrow \textrm{C}$ | $\textrm{A} \Leftrightarrow \textrm{B}\textrm{ et }\textrm{B} \Leftrightarrow \textrm{C}$ |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Donc les propositions $\textrm{A} \Leftrightarrow \left( \textrm{B} \Leftrightarrow \textrm{C}\right)$ et $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \Leftrightarrow \textrm{C}$ sont tautologiquement équivalentes. Ainsi, $\textrm{A} \Leftrightarrow \left( \textrm{B} \Leftrightarrow \textrm{C}\right)$ et $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \Leftrightarrow \textrm{C}$ sont bien des propositions équivalentes, ce qui prouve que l’équivalence est associative. Mais, quand les mathématiciens écrivent $\textrm{A} \Leftrightarrow \textrm{B} \Leftrightarrow \textrm{C}$, ils pensent à $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \textrm{ et } \left( \textrm{B} \Leftrightarrow \textrm{C} \right)$, alors que ce ne sont pas des propositions logiques équivalentes (voir la table de vérité).
Par conséquent, le fait que l’énoncé $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \textrm{ et } \left( \textrm{B} \Leftrightarrow \textrm{C} \right)$ s’écrive $\textrm{A} \Leftrightarrow \textrm{B} \Leftrightarrow \textrm{C}$ est seulement une convention d’écriture.
Remarque : Quand dans les livres, on lit "Les trois propositions suivantes sont équivalentes", il s’agit de $\left( \textrm{A} \Leftrightarrow \textrm{B} \right) \textrm{ et } \left( \textrm{B} \Leftrightarrow \textrm{C} \right)$.
2. LE RAISONNEMENT ET LA DÉMONSTRATION
2.1. Figures usuelles du raisonnement
2.1.1. Utilisation de l’implication
La proposition $\textrm{A} \Rightarrow \textrm{B}$ est une proposition conditionnelle (proposition qui s’écrit sous forme d’une implication).
Le programme appelle proposition conditionnelle les propositions qui s’écrivent sous forme d’implication :
$\forall x \left( \textrm{A}\left[ x \right] \Rightarrow \textrm{B}\left[ x \right] \right) $.
Pour démontrer cette proposition, on va écrire :
- Soit x un élément du référentiel V.
- Supposons que $\textrm{A}\left[ x\right] $ soit vrai.
- ...
- ...
- D’où il résulte que $\textrm{B}\left[ x\right] $ est vrai.
- Donc je viens de démontrer que l’on a bien : $\forall x \left( \textrm{A}\left[ x \right] \Rightarrow \textrm{B}\left[ x \right] \right) $.
On ne doit pas oublier de récapituler !
La phrase :
"x peut se mettre sous la forme au + bv, avec u et v dans Z"
doit plutôt s’écrire :
"x peut se mettre sous la forme au + bv, pour au moins un u et un v dans Z".
L’élève doit comprendre les quantificateurs sous-entendus dans une phrase.
Prenons par exemple :
La preuve commencerait par :
- Soit $n$ un entier $\geq 0$
- ...
- ...
- Conclusion : j’ai pu trouver quatre entiers a, b, c, d tels que $n=a^2+b^2+c^2+d^2$. Ce qui s’écrira donc :
$\forall n \quad \exists \, a \, \exists \, b \, \exists \, c \, \exists \, d \, \qquad n=a^2+b^2+c^2+d^2$.
Il faut que la phrase permette à l’élève de rétablir la quantification existentielle. On préfèrera dire :
On se place dans R. Un nombre est algébrique s’il est solution d’une équation à coefficients entiers. On a :
$ \forall \, x \left( x \textrm{ est alg\’ebrique ou } x \textrm{ est irrationnel}\right).$
Voici deux énoncés existentiels :
- $\gamma$ étant la constante d’Euler, $\left( \exists p \in \textbf{N}\right) \left( \exists q \in \textbf{N}^* \right) \gamma= \frac{p}{q}$ (énoncé non démontré aujourd’hui, d’ailleurs probablement faux).
- $\exists x \left( x \in \textbf{C} \textrm{ et } x^2+1=0 \right)$ (proposition vraie).
Pour démontrer qu’une proposition est fausse, il ne suffira donc pas de donner un contre-exemple (cette idée généralement répandue est fausse). Elle n’est vraie que pour les propositions où il y a $\forall$.
Dans le programme de seconde, on doit mettre en évidence le quantificateur sous-entendu dans une proposition.
- $\left( \forall x \right) \textrm{A} \Rightarrow \textrm{B} $ : proposition conditionnelle directe.
- $\left( \forall x \right) \textrm{B} \Rightarrow \textrm{A} $ : proposition réciproque.
- $\left( \forall x \right) \textrm{non B } \Rightarrow \textrm{ non A} $ : proposition contraposée.
- $\left( \exists x \right) \textrm{non} \left( \textrm{A}\Rightarrow \textrm{B} \right) $, c’est-à-dire $ \textrm{A} \textrm{ et } \textrm{ non B} $ : négation de la proposition.
Théorème : Toute proposition conditionnelle est synonyme de sa contraposée.
- Exemples :
- $ \textrm{A} \Rightarrow \textrm{B} $ : Si $n^2$ est impair, alors n est impair.
- $ \textrm{non} \left( \textrm{A}\Rightarrow \textrm{B} \right) $ : Si n n’est pas impair, alors $n^2$ n’est pas impair.
- $n \textrm{ pair} \Rightarrow n^2 \textrm{ pair}$.
Pour savoir si un "si" a un sens mathématique, il faut savoir s’il est contraposable. Sa contraposée doit avoir un sens. L’implication n’est pas le si de la langue courante.
Certaines implications mathématiques posent problème :
$\textrm{Si } a \textrm{ et } b \textrm{ sont des réels strictement positifs, alors : } \ln(ab)=\ln a +\ln b$.
La contraposée donne :
Si $\ln(ab) \neq \ln a + \ln b \textrm{ alors } a \leq 0 \textrm{ ou } b \leq 0 $ (!!) ; et donc elle n’a pas de sens.
Pour que $\left( \textrm{A}\left[ x \right] \Rightarrow \textrm{B}\left[ x \right] \right) $ ait un sens, il faut que les propriétés $ \textrm{A}\left[ x \right] $ et $ \textrm{B}\left[ x \right] $ aient un sens pour tous les $x$ du référentiel.
Donc la proposition donnée plus haut n’est pas une implication. Cette forme de phrase est seulement destinée à cacher des quantificateurs dont on a peur. La phrase correcte est :
$\forall \, a \, \in \textbf{R}^+ \quad \forall \, b \, \in \textbf{R}^+ \quad \ln(ab)=\ln a +\ln b$.
Les différentes formulations de l’implication
Voici un exercice hygiénique à pratiquer trois minutes par jour : classer toutes les phrases ci-dessous en deux catégories, la catégorie $\textrm{A} \Rightarrow \textrm{B}$ et la catégorie $\textrm{B} \Rightarrow \textrm{A}.$
| $\textrm{A} \Rightarrow \textrm{B}$ | $\textrm{B} \Rightarrow \textrm{A}$ | |
| A implique B | B implique A | A seulement si B |
| Si A alors B | Si B alors A | B seulement si A |
| Si A, B | Si B, A | A est une condition suffisante pour B |
| A est une condition nécessaire pour B | ||
| B est une condition suffisante pour A | ||
| B est une condition nécessaire pour A | ||
| Pour que A, il faut que B | A dès que B | |
| Pour que B, il faut que A | Dès que B, A | |
| Pour que A, il suffit que B | B dès que A | |
| Pour que B, il suffit que A | Dès que A, B | |
| B exige A | A exige B | |
| B suppose A | A suppose B | |
| Pour que A, il est indispensable que B | ||
| Pour que A, il est nécessaire que B | ||
| Pour que B, il est indispensable que A | ||
| Pour que B, il est nécessaire que A |
Cela donne :
| $\textrm{A} \Rightarrow \textrm{B}$ | $\textrm{B} \Rightarrow \textrm{A}$ | |
| A implique B | B implique A | |
| Si A alors B | Si B alors A | |
| Si A, B | Si B, A | |
| A seulement si B | B seulement si A | |
| A est une condition suffisante pour B | B est une condition suffisante pour A | |
| B est une condition nécessaire pour A | A est une condition nécessaire pour B | |
| Pour que A, il faut que B | Pour que B, il faut que A | |
| Pour que B, il suffit que A | Pour que A, il suffit que B | |
| B dès que A | A dès que B | |
| Dès que A, B | Dès que B, A | |
| A exige B | B exige A | |
| A suppose B | B suppose A | |
| Pour que A, il est indispensable que B | Pour que B, il est indispensable que A | |
| Pour que A, il est nécessaire que B | Pour que B, il est nécessaire que A |
IFS : Il faut et il suffit
Pour que A, IFS B.
- Il faut :
- Je suppose que A est vrai
- ...
- donc B est vrai.
- Il suffit :
- Je suppose que B est vrai
- ...
- donc A est vrai.
- cqfd.
"Pour que A, il faut et il suffit que B" veut dire : "pour que A, il faut que B" et "pour que A, il suffit que B".
Remarques diverses
Place des quantificateurs : Soit f une transformation du plan. f est une homothétie ou une translation ssi
$\exists k \in \textbf{R} \, \forall\, \textrm{A}\, \forall \, \textrm{B} \qquad \overrightarrow{f(\textrm{A})f(\textrm{B})}=k\overrightarrow{\textrm{A}\textrm{B}}$
- Exercice : Montrer que f est une homothétie ou une translation ssi
$ \forall\, \textrm{A}\, \forall \, \textrm{B} \,\,\exists k \in \textbf{R}\quad \overrightarrow{f(\textrm{A})f(\textrm{B})}=k\overrightarrow{\textrm{A}\textrm{B}}$
est vraie.
Halte ou je tire !
Si tu ne t’arrêtes pas, je tire.
Tu ne t’arrêtes pas $\Rightarrow$ je tire.
Cela illustre la synonymie entre :
$\textrm{A}\Rightarrow \textrm{B} \sim \textrm{non A ou B}$
$\textrm{non A}\Rightarrow \textrm{B} \sim \textrm{A ou B}$.
La contraposée est "Si je ne tire pas, c’est que tu t’es arrêté."
Les mathématiques sont intemporelles.
A, donc B (Règles de déduction)
Je sais 2 choses :
- $\textrm{A} \Rightarrow \textrm{B}$ est vrai.
- A est vrai.
J’en déduis que B est vrai.
Autrement dit, de $\textrm{A} \Rightarrow \textrm{B}$ et de A, je peux déduire B.
Axiomes + règles de déduction s’appelle en logique un système de déduction.
- Exemple : Le système de Hilbert
- 1re règle : de $\textrm{A} \Rightarrow \textrm{B}$ et de A, je peux déduire B. C’est le MODUS PONENS (latin : ponere = poser) ou règle de détachement.
- 2e règle : la règle de généralisation. Si j’ai déjà déduit A[x] (sans hypothèse sur x), alors je peux déduire $\forall\, x \, \textrm{A}[x]$.
Hilbert voulait créer un paradis des mathématiques : la théorie des ensembles dans laquelle n’importe quelle vérité peut être obtenue par un processus fini de règles de déduction (par démonstration formelle). Gödel a anéanti ce projet en démontrant l’indécidabilité de certaines propositions.
La phrase "A, donc B" n’a aucun rapport avec "$\textrm{A} \Rightarrow \textrm{B}$". Il ne faut pas utiliser le signe $\Rightarrow$ comme abréviation du mot donc.
Remarque sur l’implication : n est premier implique n est impair. En langage naturel, deux propositions ne s’assemblent pas à l’aide d’un verbe conjugué. Donc naturellement, l’enseignant va plutôt dire : n premier implique n impair (le fait que n soit premier implique le fait que n soit impair). On traite le mot "implique" comme un verbe et non pas comme un connecteur.
Conclusion : ne pas commencer une démonstration par "si", mais plutôt par : je sais que... donc..., on a... donc...
2.1.2. Raisonnement par conditions nécessaires
Problème typique : les problèmes de lieux
Déterminer l’ensemble $ \textrm{E}= \left\lbrace \textrm{M}\,\in \,\textbf{P} \, /\, \textrm{MA}^2 - \textrm{MB}^2 = 3 \right\rbrace $.
1) Analyse : Soit M un point du plan tel que $ \textrm{MA}^2 - \textrm{MB}^2 = 3 $
- Je sais que $\textrm{MA}^2 - \textrm{MB}^2 = 3$.
- On a donc...
- alors la condition X(M) est vérifiée.
Supposons que l’on ait : X(M) $\Rightarrow$ M est situé sur la droite D. Alors M $\in$ D.
2) Synthèse : Est-ce que cela suffit ?
- Soit M $\in$ D
- ...
- $\textrm{MA}^2 - \textrm{MB}^2 = 3$.
L’ensemble cherché est donc la droite D.
2.1.3. Raisonnement par contraposition
Je veux prouver que $\textrm{A} \Rightarrow \textrm{B}$. J’utilise l’équivalence entre "$\textrm{A} \Rightarrow \textrm{B}$" et "$\textrm{non B} \Rightarrow \textrm{A}$". Je suppose que non B est vrai (i. e. que B est faux), je prouve alors que A est faux, donc non A est vrai.
- Exemple : inégalité triangulaire et points alignés.
2.1.4. Utilisation du principe du tiers exclu
2.1.5. Raisonnement par l’absurde
Je suppose que A est vrai et que B est faux, et j’en déduis une contradiction.
- Exemple : unicité de la limite.
Il faut prévenir les élèves dès le départ que l’on émet une hypothèse en vue d’établir une contradiction. Il faut délimiter les phases du raisonnement et c’est fondamentalement important de le faire dans le cas du raisonnement par l’absurde.
2.1.6. Raisonnement par équivalences
2.1.7. Raisonnement par disjonction de cas (principe du tiers-exclu)
Soit x un réel.
- 1er cas : $x\,\in \textrm{A}$... alors P(x)
- 2e cas : $x\,\in \textrm{B}$... alors P(x)
- 3e cas : $x\,\in \textrm{C}$... alors P(x)
(A, B, C) étant une partition de R (i. e. on doit avoir la condition $\textrm{A}\cup\textrm{B}\cup\textrm{C}=\textbf{R}$, on peut conclure que tout nombre réel x a la propriété P(x).
- Exemple : Prouver l’existence de nombres irrationnels strictement positifs a et b tels que $a^b \,\in \, \textbf{Q}$.
Posons $x=\sqrt{2}$ et $y=\sqrt{2}$.
- 1er cas : $x^y \,\in\, \textbf{Q}$. Victoire : je prends $a=b=\sqrt{2}$.
- 2e cas : $x^y \,\notin\, \textbf{Q}$. Prenons alors $a=x^y$ et $b=\sqrt{2}$. On a :
$a^b=\left( {x^y}\right) ^{\sqrt{2}}=\left( {\left( {\sqrt{2}}\right) ^{\sqrt{2}}} \right) ^{\sqrt{2}}=\sqrt{2}^{\sqrt{2}*\sqrt{2}}=\sqrt{2}^2=2$.
Je prends $a=x^y \notin \textbf{Q}$ et $b=\sqrt{2} \notin \textbf{Q}$ (en réalité $(\sqrt{2})^{\sqrt{2}} \notin \textbf{Q}$, donc on est dans le 2e cas).
Pour les intuitionnistes, ce raisonnement n’est pas valable car il n’est pas constructif (on n’exhibe pas les réels x et y).
2.1.8. Utilisation d’exemples et de contre-exemples
2.1.9. Raisonnement par récurrence
Soit P une propriété (P[n]).
- 1re formulation :
Si P(0) est vrai et si, pour chaque entier k, l’implication $\mathrm{P}\left[ k\right] \Rightarrow \mathrm{P}\left[ k+1\right] $ est vraie, alors, pour tout n, P[n] est vraie.
Variante :
$\left( \textrm{P}\left[ 0\right] \textrm{ et } \forall\, k \left( \textrm{P}\left[ k\right] \Rightarrow \textrm{P}\left[ k+1\right] \right) \right) \Rightarrow \forall\, n\quad \textrm{P}\left[ n\right] $
Axiome de base : Toute partie non vide de N admet un plus petit élément.
À partir de cet axiome, on peut établir le raisonnement par récurrence comme étant un théorème. Démonstration par l’absurde :
Supposons P[0] vrai et pour chaque entier k, $\textrm{P}\left[ k\right] \Rightarrow \textrm{P}\left[ k+1\right] $ vrai, et il existe un entier n tel que P[n] soit faux. L’ensemble des entiers tels que P[n] soit faux est donc une partie non vide de N donc elle admet un plus petit élément. Soit b le plus petit des entiers tels que P[n] soit faux. P[b] est faux et pour tout a < b, P[a] est vrai. b – 1 existe dans N (b ≠ 0). b – 1 < b, donc P[b – 1] est vrai. P[b – 1 + 1] est vrai donc P[b] est vrai. Contradiction.
- Exemple :
- Fibonacci : $\textrm{F}_0=\textrm{F}_1=1 \textrm{ et } \forall n \quad\textrm{F}_{n+2}=\textrm{F}_{n+1}+\textrm{F}_n$.
- $ \forall n \quad\textrm{F}_{n+1}=\textrm{F}_{n}\textrm{F}_{n+2}+(-1)^{n+1}$.
- 2e formulation (récurrence sur l’ensemble des entiers antérieurs) :
Si P[0] est vrai et si, pour chaque entier k, $\left( \forall \, h < k \quad \textrm{P}\left[ h \right] \right) \Rightarrow \textrm{P}\left[ k \right]$, alors pour tout n, P[n] est vraie.
Ce théorème se démontre avec l’axiome de base ci-dessus. La formulation 2 du raisonnement par récurrence est plus forte que la formulation 1 et il est facile de démontrer que 2 implique 1.
- Exemple où on utilise le théorème 2 : Tout entier $\geq 2$ a au moins un diviseur premier.
2.2. Rédiger une démonstration
Conseil : il vaut mieux éviter l’utilisation du signe $\Rightarrow$ comme métalangage. De même que le signe $\Leftrightarrow$. On préférera écrire "ssi".
3. LANGAGE ENSEMBLISTE - CARDINALITÉ
3.1. Appartenance, inclusion
3.2. Deux façons principales de définir un ensemble
3.3. Opérations ensemblistes élémentaires
| Opérations ensemblistes | Connecteurs | Parties d’un ensemble E |
| $\cap$ | et | $\textrm{A} \cap \textrm{B}=\left\lbrace x\,\in\,\textrm{E}\,/\,x\,\in\,\textrm{A}\textrm{ et }x \,\in\,\textrm{B} \right\rbrace $ |
| $\cup$ | ou | $\textrm{A} \cup \textrm{B}=\left\lbrace x\,\in\,\textrm{E}\,/\,x\,\in\,\textrm{A} \textrm{ ou }x \,\in\,\textrm{B} \right\rbrace $ |
| $ \complement_{E}$ | non | $ \complement_{E}A=\left\lbrace x\,\in\,\textrm{E}\,/\,\textrm{non }\left( x \,\in\,\textrm{A}\right) \right\rbrace $ |
3.4. Lien avec les connecteurs (attention à l’implication)
| Relation binaire | Connecteur | Parties d’un ensemble E |
| $\subset$ | $\Rightarrow$ | $\left( \complement_{E}\textrm{A}\right) \cap \textrm{B} = \left\lbrace x\,\in\,\textrm{E}\,/\,x \,\in\,\textrm{A} \Rightarrow x \,\in\,\textrm{B} \right\rbrace$ |
Étant donné deux parties A et B, $\textrm{A} \subseteq\textrm{B}$ ssi
$\underbrace{\forall \,x\,\in \,\textrm{E}\,\left( \,x\,\in \,\textrm{A}\Rightarrow \,x\,\in \,\textrm{B}\right) }_{\textrm{Relation binaire}}$
3.5. Lien avec les probabilités
3.6. Cardinalité des ensembles finis
3.7. Lien avec la combinatoire et les probabilités
3.8. À propos des ensembles infinis
4. PANORAMA
Aperçu sur ce qu’est la logique mathématique aujourd’hui, à travers deux de ses domaines : la théorie des modèles et la théorie des ensembles
Une notion centrale : celle de modèle.
Une théorie est un ensemble de propriétés. Les propriétés qui sont dans la liste sont appelées les axiomes de la théorie.
On écrit $\textrm{M} \models\textrm{T}$, où M est une structure, T une théorie et $\models$ représente le symbole de satisfaction. Cette phrase se lit : "la structure M satisfait la théorie T" ou "la structure M est un modèle de la théorie T".
Ce mot modèle n’est pas à prendre au sens de modélisation. Un modèle au sens de la modélisation est une représentation mathématique à partir d’une situation concrète (on parle de modélisation mathématique, de modèle mathématique). Le modèle dans ce sens-là est abstrait, à partir d’une expérience concrète. En logique, c’est le contraire : un modèle logique est concret.
Exemple : Z est un modèle des anneaux commutatifs... qui satisfait la théorie...
Le mathématicien étudie des structures, c’est à dire des ensembles munis de relations, de fonctions, d’éléments distingués, de familles, de sous-ensembles. Il en étudie certaines individuellement, en essayant de les décrire, d’en dégager des propriétés.
- Exemples :
- $\left\langle \textbf{Z},+,*,0,1 \right\rangle $ , $\left\langle \textbf{R},+,*,0,1 \right\rangle $ , $\left\langle \textbf{R}\left[ \textrm{X}\right] ,+,*,0,1 \right\rangle $ sont trois structures de même type.
- $\left\langle \textbf{R},\leq \right\rangle $ est une structure d’un autre type.
- Prenons la structure des corps algébriquement clos de caractéristique 0 (c’est à dire $ 1+1+1+\dots+1 $ n’est jamais égal à 0). Q n’en est pas un modèle. C est un modèle de cette structure. C est le seul corps de caractéristique 0 de sa cardinalité ($2^{\aleph_0}$ cardinalité de C), car tout modèle de cette structure qui a la cardinalité de C est isomorphe à C.
Le socle de la logique, c’est la notion de modèle de théorie. Le calcul des propositions et le calcul des prédicats forment l’outillage commun à ce socle.
Complétude
Définition : Une formule (sans variable libre) est conséquence d’une théorie T
- (version 1 : conséquence sémantique) si elle est vraie dans tous les modèles de T
- (version 2 : conséquence syntaxique) si je peux donner de cette formule une démonstration formelle à partir d’un système de règles de déductions et d’axiomes.
Théorème de complétude de Gödel (1928)
Une formule est conséquence sémantique d’une théorie ssi elle en est conséquence syntaxique.
- Exemple : unicité de l’élément neutre :
$\forall \, x\, \left( \forall\,y\,\left[ x.y=y.x \textrm{ et } x.y=y \right] \Rightarrow x=e \right) $
C’est une conséquence de la théorie des groupes suivant la version 1.
On peut décrire toutes les mathématiques par la logique avec la théorie suivante : LA THÉORIE DES ENSEMBLES.
$1=\left\lbrace \varnothing \right\rbrace $
$2=\left\lbrace 0,1 \right\rbrace $
$3=\left\lbrace 0,1,2 \right\rbrace$, etc.
Axiome de la paire : $ \forall\,x\,\forall\, y \quad \exists\, z \, \forall \, t \, \left( t\,\in\,\textbf{Z} \Rightarrow \left( t=x \vee t=y\right) \right) $.
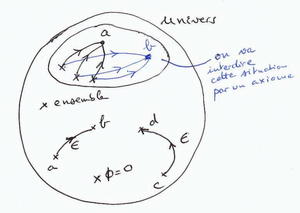
Toutes les propriétés des mathématiques peuvent s’écrire à l’aide de seulement les deux symboles = et $\in$ (plus les connecteurs logiques bien sûr).
Théorie de ZERMELO-FRENCKEL (ZF)
Existe-t-il un modèle ? La théorie est consistante si elle admet un modèle. Gödel a prouvé qu’on ne pouvait pas trouver de tel modèle.
Si une théorie a un modèle, alors elle en a une infinité. Une théorie contradictoire est une théorie qui n’a pas de modèle.
| Contradictoire | Consistante |
| T n’a pas de modèle | T a un modèle |
Théorème non démontré (**) : Toute partie de R est soit dénombrable (donc de même cardinalité que N), soit équipotente à R.
Gödel a dit que si la théorie ZF n’est pas contradictoire, alors ... il y aura des univers avec l’hypothèse du continu et il y aura aussi des univers qui vérifient (**).
Il n’y a aucun espoir de démontrer que la théorie des ensembles est non-contradictoire.
Il y a plusieurs univers mathématiques. Une axiomatique pour les mathématiques induit obligatoirement plusieurs univers mathématiques. Il n’y aura donc pas unicité de l’univers si on veut construire une axiomatique pour la théorie des ensembles.

Commentaires