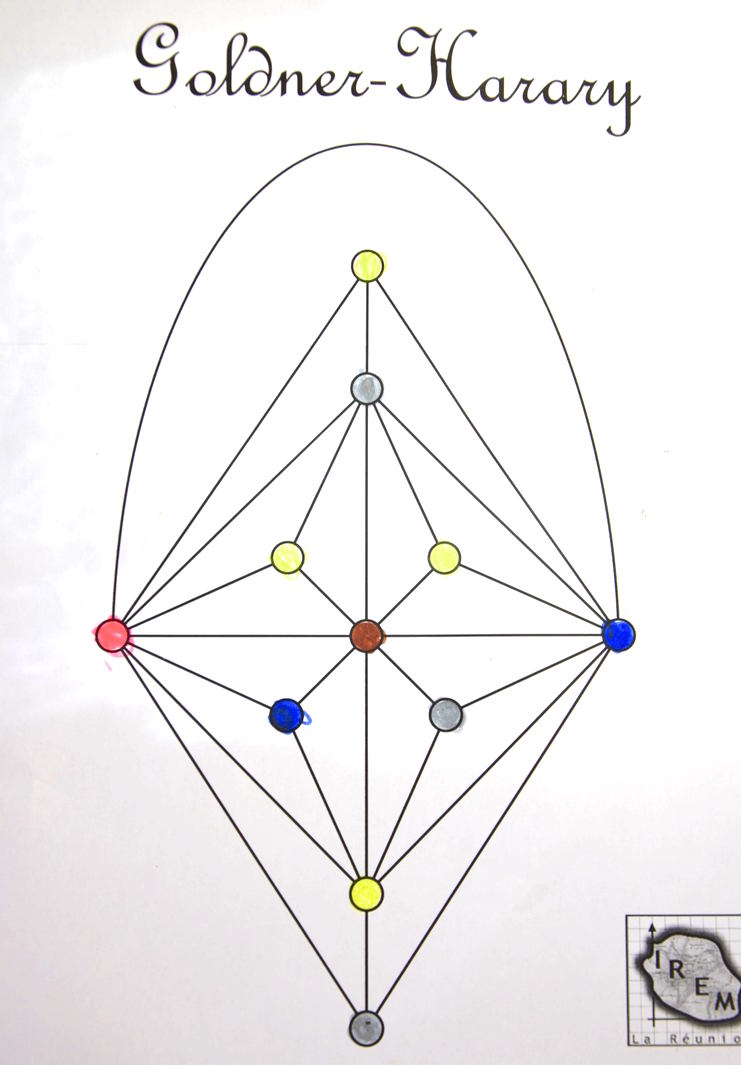
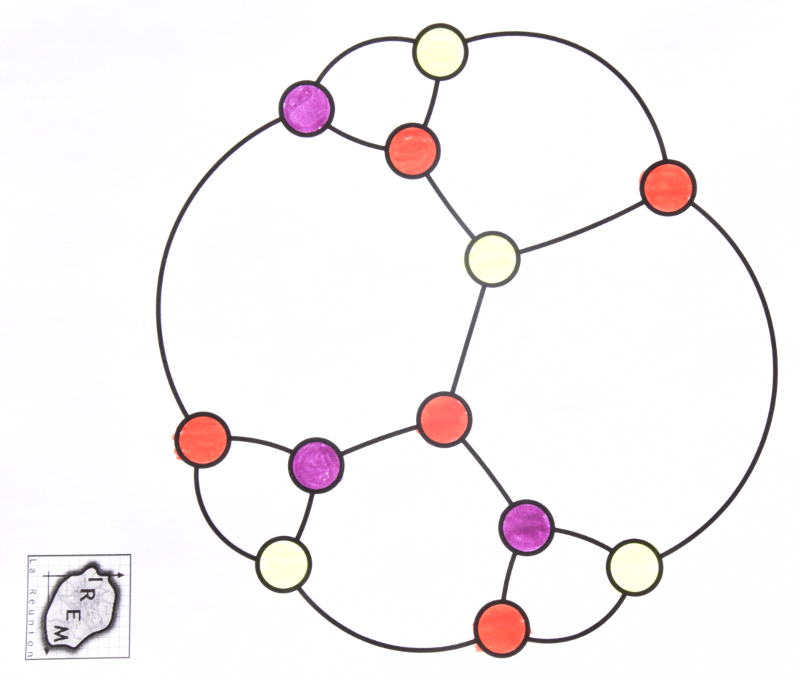
Par exemple, il ne faut qu’une fraction de seconde pour vérifier que le graphe de Goldner-Harary a été correctement colorié :
Cela « saute aux yeux ». Mais pour obtenir cette coloration, cela a pris plusieurs minutes même en coloriant rapidement les sommets.
Par exemple voici le graphe de Goldner-Harary colorié en 5 couleurs, en 2 minutes, par une élève de CM1 :
Il y a du rouge, du bleu, du jaune, du gris et du marron : Cela fait bien 5 couleurs [1].
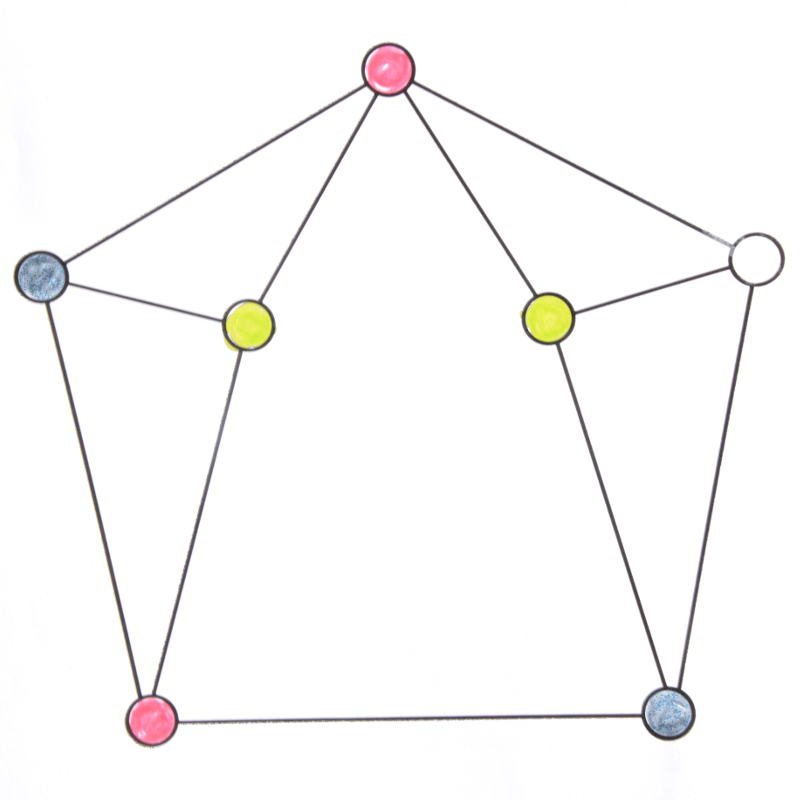
Le même graphe, colorié par un élève de CP (là encore en quelques minutes) :
Là encore on dénombre 5 couleurs : rouge, noir, magenta, cyan ... et le dernier sommet est resté blanc (c’est une couleur) faute de réussir à le colorier dans une des 4 couleurs précédentes : Il est adjacent à des sommets déjà coloriés dans les 4 couleurs en question.
Lorsque cela prend beaucoup moins de temps pour vérifier qu’une solution est bonne, que pour trouver une solution, le problème est dit NP [2]. L’exemple ci-dessus illustre donc le fait que colorier un graphe est un problème NP. Cela a été vu dans la dernière partie du sujet de Capes 2019. Mais la difficulté à résoudre ce problème n’est réelle que si on cherche à minimiser le nombre de crayons de couleurs utilisés.
Nombre chromatique du graphe de Goldner-Harary
Les deux élèves d’école primaire ont réussi à descendre à seulement 5 couleurs alors que le graphe comprend 11 couleurs. Beau score, mais en comptant les couleurs du premier exemple (rouge, vert, bleu, jaune) on en trouve encore moins, à savoir 4. Ceci dit, compter les couleurs prend encore beaucoup moins de temps que trouver comment colorier le graphe de Goldner-Harary en seulement 4 couleurs : Le problème reste NP.
Et en 3 couleurs ? Y a-t-il un moyen d’utiliser encore moins de crayons (se passer du jaune par exemple) pour colorier en 3 couleurs seulement ce graphe ?
La réponse est non, parce que dans le graphe de Goldner-Harary il y a un tétraèdre :
Or rien que dans cette partie du graphe, chaque sommet est adjacent à 3 autres sommets ce qui nécessite de n’utiliser chaque couleur que sur un seul de ces sommets : 4 couleurs sont nécessaires.
Cette activité permet aussi de découvrir l’énoncé du théorème des quatre couleurs : Pour colorier proprement un graphe planaire, 4 crayons suffisent (si on se débrouille bien).
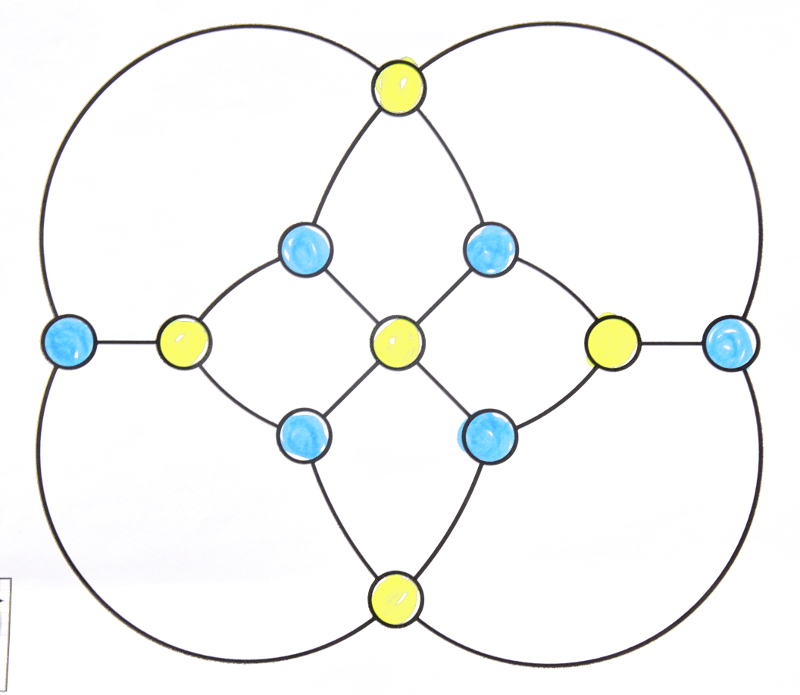
Ceci n’empêche pas que dans certains cas (autres que le graphe de Goldner-Harary) on puisse aller encore plus bas, avec par exemple 2 crayons seulement [3] pour le graphe de Herschel :
Avec correction d’une erreur
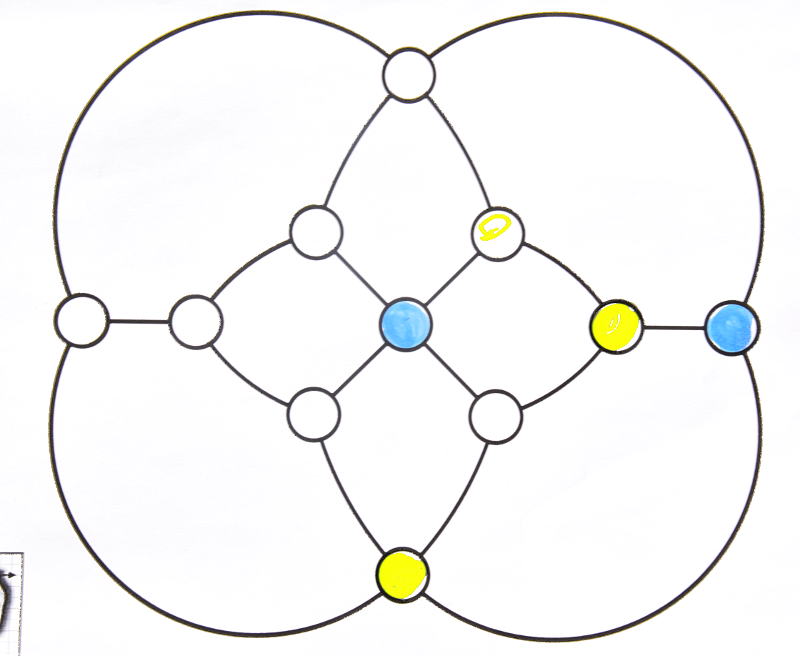
Trop de précipitation nuit à l’attention et aboutit à un début de coloriage (en jaune) d’un sommet déjà adjacent à du jaune :
Graphes du poisson, de Hajos et de Frucht
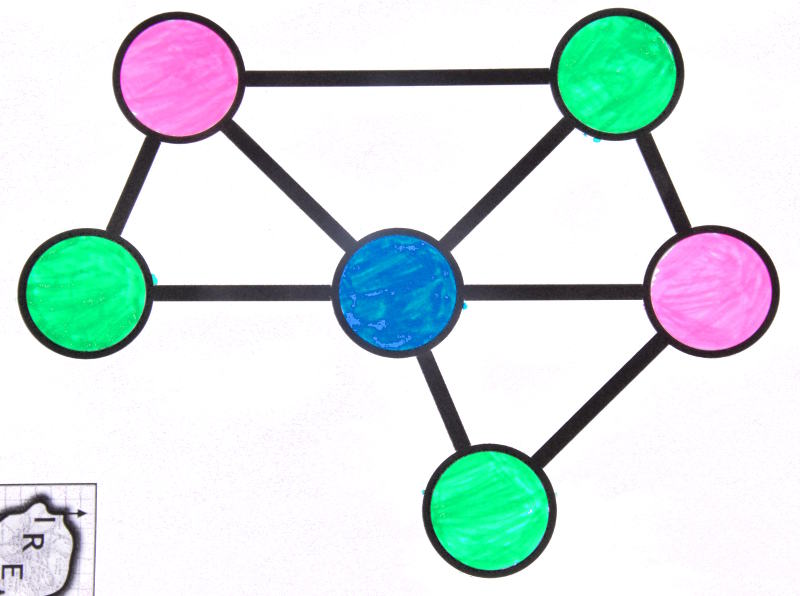
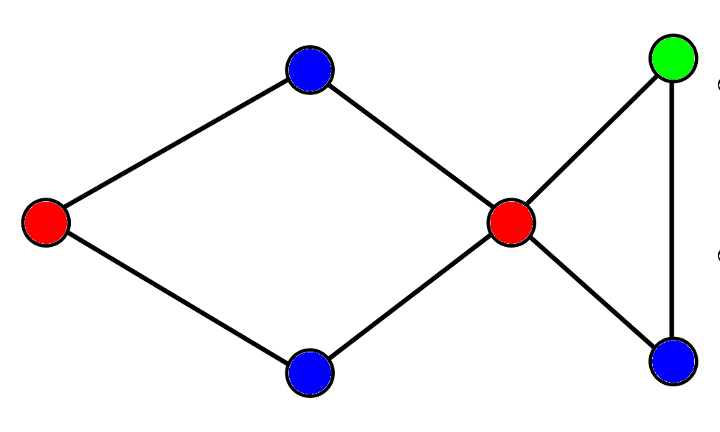
Le graphe du poisson peut être colorié en 3 couleurs seulement :
Mais on ne peut pas descendre plus bas, parce que dans le graphe du poisson il y a un triangle :
Chacun des sommets de ce triangle est adjacent aux deux autres sommets et il faut donc autant de couleurs que de sommets du triangle, soit 3 couleurs. Comme la coloration en 3 couleurs a été réussie, cela prouve que le nombre chromatique du graphe du poisson est égal à 3.
Le graphe de Hajos présente beaucoup de symétrie ce qui aboutit plus ou moins automatiquement à une coloration en 3 couleurs, elle-même très symétrique (toujours en CP) :
Ce coloriage est en général fait assez rapidement. Et comme il y a des triangles dans le graphe de Hajos, on sait qu’on ne peut pas descendre en-dessous : Le graphe de Hajos est de nombre chromatique 3.
De même la présence de triangles dans le graphe de Frucht montre qu’on ne peut pas le colorier en moins de 3 couleurs. Mais en 3 couleurs exactement on peut (CP) :
Nombre chromatique du graphe de Moser
Voici une tentative ratée (en CP) pour colorier en seulement 3 couleurs le graphe de Moser :
En effet le dernier sommet non colorié est déjà adjacent à trois sommets de couleurs différentes, et nécessite une quatrième couleur (ici le blanc, c’est une couleur).
En coloriant en premier le sommet de plus haut degré [4]. (en gris, en haut) ça devrait aller mieux. Et bien non :
De fait, le nombre chromatique du graphe de Moser est 4, bien qu’il n’y ait pas de tétraèdre dans le graphe (les difficultés ne sont pas toujours locales).
Graphe de Bidiakis et prisme pentagonal
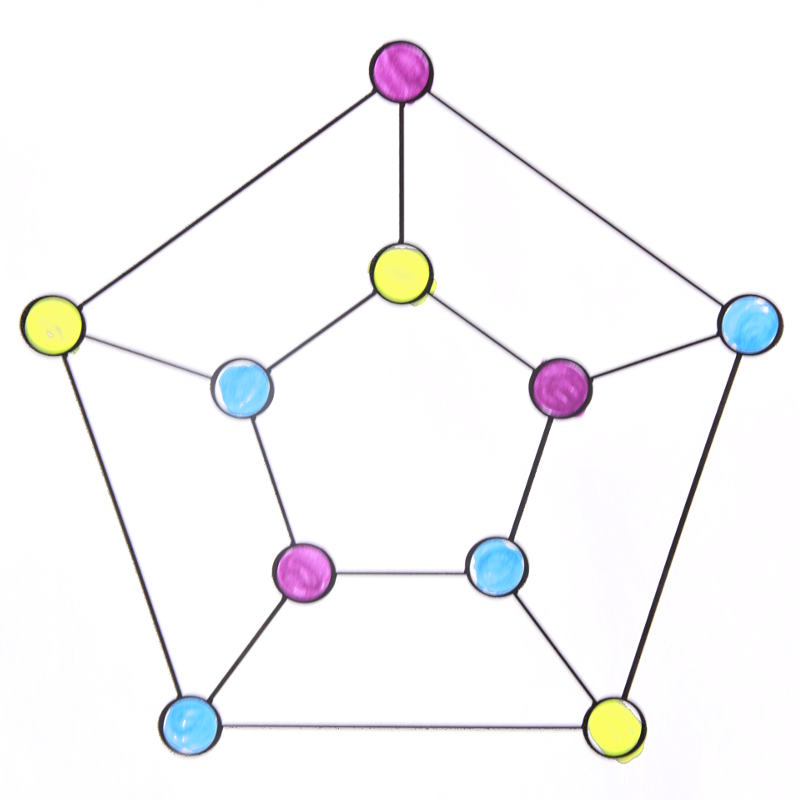
Bien qu’ilsne comprennent pas de triangles, le graphe de Bidiakis et le prisme pentagonal ne peuvent pas être coloriés en moins de 3 couleurs. Mais on peut colorier le cube de Bidiakis avec seulement 3 crayons :
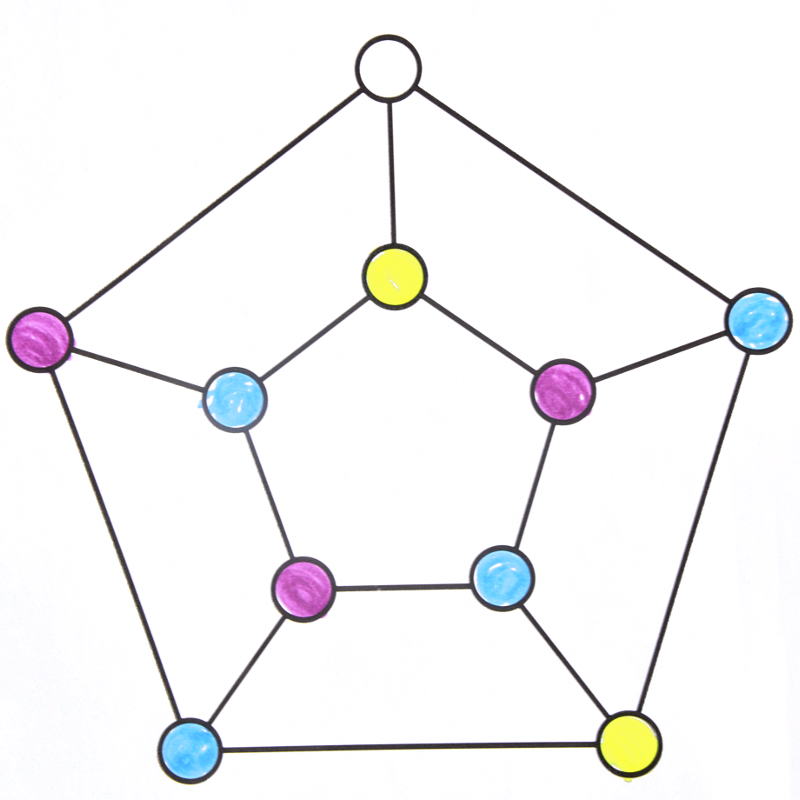
Pour le prisme pentagonal ça ne marche pas :
Mais en s’y prenant autrement, si :
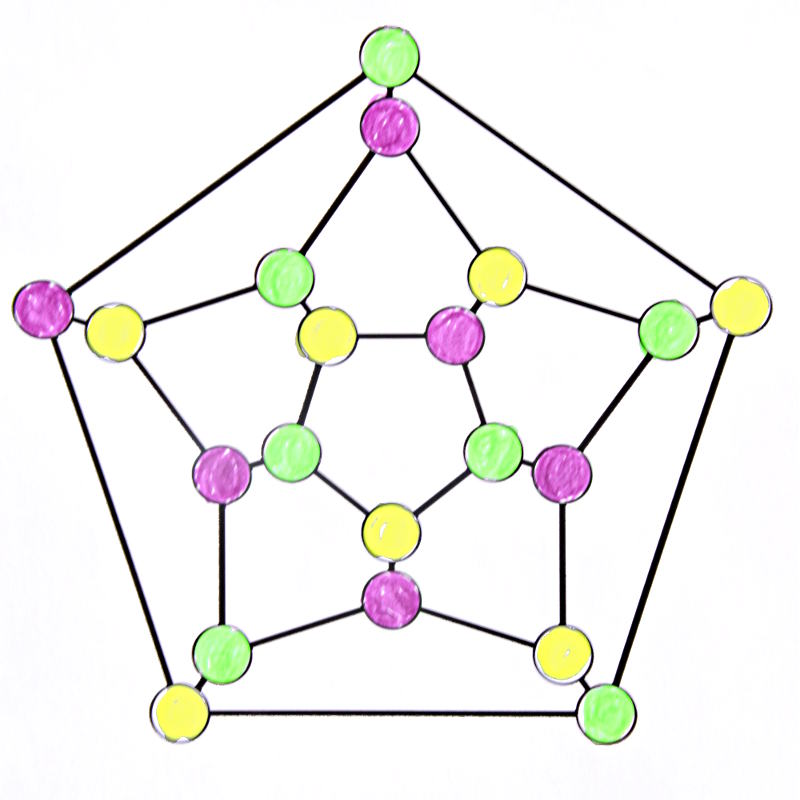
Pour finir en beauté, comme le dodécaèdre comporte des pentagones qu’il est impossible de colorier en moins de 3 couleurs, on a la preuve (CP) que son nombre chromatique est 3, en le coloriant avec seulement 3 crayons.
Apparemment ce n’est pas si facile quand on arrive à deux sommets adjacents qui ne peuvent être coloriés ni en vert ni en mauve :
Mais en s’y prenant autrement, on finit par y arriver :
Commentaires