Grille à la craie
Avant de peindre le graphe, il a fallu décider de la forme de celui-ci : Épaisseur et longueur des arêtes, forme et dimensions des sommets. C’est la version Pàcom qui a été retenue :
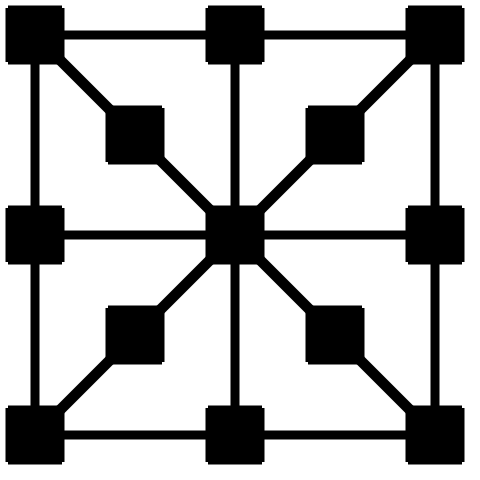
Outre le fait que la semaine des maths a permis d’évaluer la visibilité de ce graphe par les joueurs, on constate qu’il s’inscrit bien dans une grille de 9×9 carrés. La première étape consiste donc à dessiner à la craie une telle grille. On a choisi que les sommets mesurent 50cm de côté donc la grille occupe un grand carré de 4,5m de côté. Pour commencer, comment avoir un angle droit en ne disposant pas d’une équerre de telles dimensions ?
On a fait comme les égyptiens de l’antiquité, qui après chaque crue du Nil, redessinaient les champs avec une corde à douze nœuds. En l’occurence, disposant de 2 rubans métalliques (gradués) de 5m de long chacun, on a tracé un trait de 4m sur une partie du sol qui semblait bien perpendiculaire au bâtiment D, puis on a utilisé les deux mètres à ruban pour dessiner un point distant à la fois de 3m de l’une des extrémités, et de 5m de l’autre :
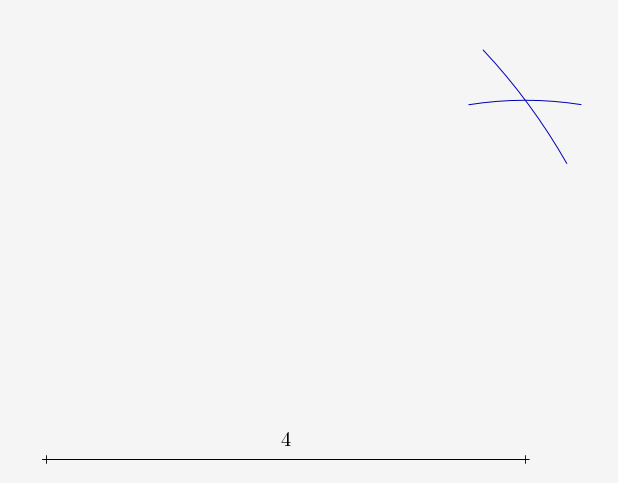
D’après la réciproque de Pythagore, on a un angle droit en bas à droite de la figure :
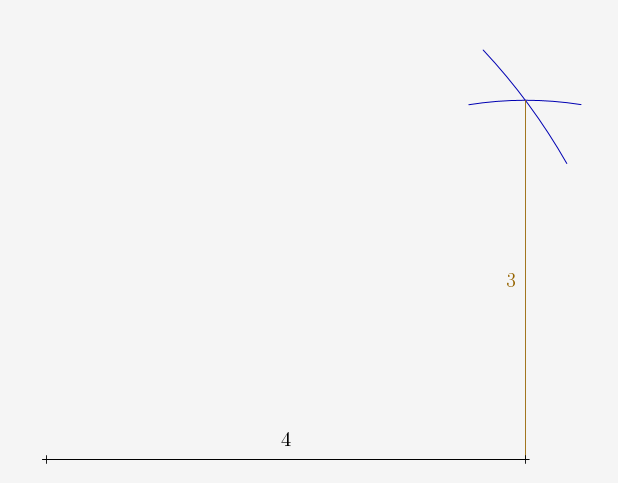
On prolonge donc les côtés de cet angle droit pour avoir deux côtés du carré, de 4,5m chacun :
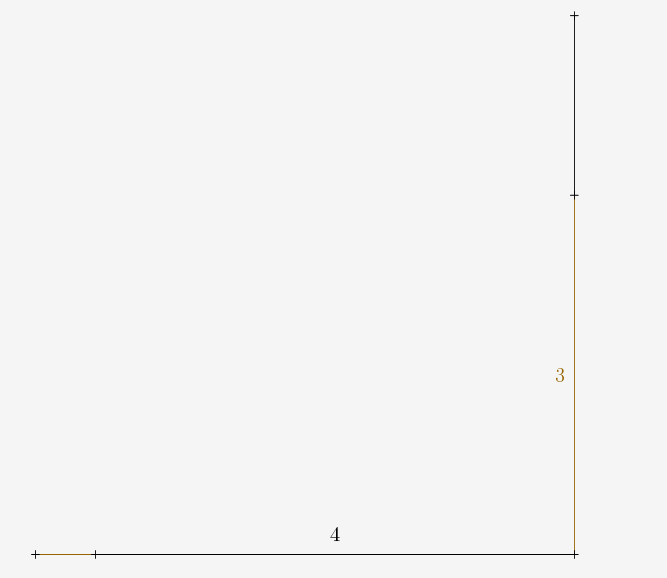
Ensuite on peut graduer ces deux côtés avec les mètres à ruban et la craie. On pose une marque tous les 50cm :
Comment compléter le carré en ayant des angles bien droits ? On a choisi de reporter 4,5m à partir de chacun des sommets libres :

On a ainsi un losange (puisque les 4 côtés mesurent 4,5m) avec un angle droit : C’est un carré. On répète sur les deux nouveaux côtés du carré l’opération de graduation tous les 50cm, puis on joint chaque graduation d’un côté, à la graduation qui lui fait face :

Ensuite, on a répété la division en graduant tous les 50cm, sur chaque trait, afin de garantir l’alignement, et vérifier que les traits sont bien droits : Ils serviront de guides au masquage. Enfin (en tout cas pour la phase craie) on a joint toutes ces graduations et complété la grille :



Masquage des arêtes du graphe
Un point de peinture a été déposé vers le centre de chacun des sommets du graphe, afin d’éviter les erreurs de parallaxe. Comme chaque sommet est un carré de 50cm de côté, en repérant (à la craie) les longueurs 21cm et 29cm, on a une longueur de 50-(21+48)=8cm au milieu du sommet :
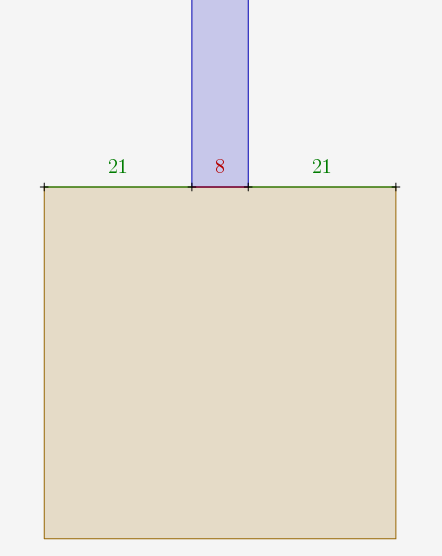
C’est de là que partira le masquage des arêtes perpendiculaires. Pour les arêtes obliques, on veut aussi une largeur de 8cm, et se pose donc la question de la distance à chaque sommet du carré de 50cm : Pythagore revient à la rescousse, avec d²+d²=8² d’où d²=32 et d=5,6cm à 1mm près. Ces longueurs de 5,6cm sont reportées à la craie, à partir du sommet du carré (le sommet du sommet !) :

En bleu, la zone qui sera peinte (arête du graphe) et donc pas masquée :
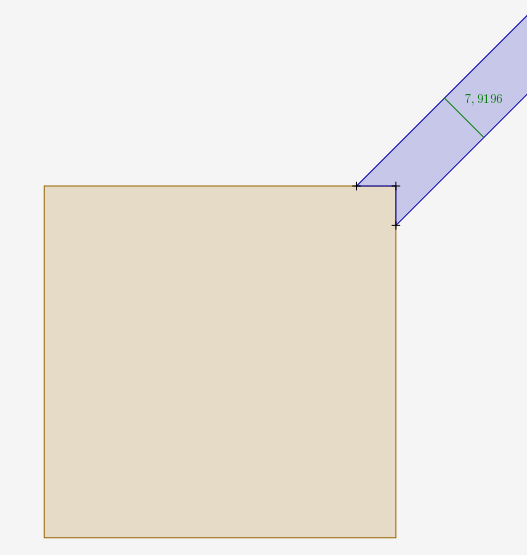
CaRMetal confirme que l’épaisseur de l’arête sera bel et bien proche de 8cm.
Une fois ces nombreuses marques à la craie effectuées, on pose du ruban de masquage de part et d’autre de chaque arête :

Puis on peint :

La planche maintenue à côté de la bombe de peinture a pour but d’éviter de peindre ailleurs qu’à l’endroit souhaité. Malgré cela il y avait tellement de vent que des artefacts seront visibles sur certaines des photos ci-dessous. Mais une autre erreur à éviter lorsqu’on veut se lancer dans cette aventure, est de marcher sur la peinture encore fraîche :

Après une pause d’un quart d’heure (le temps de laisser sécher la peinture), on a passé la seconde couche, homogénéisant ainsi l’aspect des arêtes.

Une fois le ruban de masquage enlevé (après une seconde pause de 10 mn) on pourrait presque déjà jouer sur le graphe :

Après plus de deux heures, il ne reste plus qu’à peindre les sommets
Sommets du graphe
Pour peindre les sommets, on disposait d’un gabarit de forme carrée et de 50cm de côté intérieur. Il a suffi de poser ce cadre sur une des grilles du grand carré, et de donner un coup de bombe à l’intérieur. Manquant un peu de peinture, il a été plus prudent d’opérer par petites touches, en commençant par les bords :

Le cadre est à droite de la photo. Les bords des sommets sont encore fins mais on peut déjà jouer sur ce graphe. La suite n’est que fignolage.
Après un deuxième passage les bords des sommets sont déjà plus épais :

Après un troisième passage il ne reste presque plus de peinture dans la dernière bombe [1] :


Time-lapse de la réalisation du graphe
Durant la réalisation au sol de ce graphe, soit environ 1h30 si l’on ne comptabilise que les moments où il y a action réelle(les temps d’observation/discussion ne sont pas comptabilisés), une photo a été prise toutes les cinq secondes. Ce qui fait environ 5400 photos que l’on peut alors parcourir à la cadence de de 20 images par seconde pour obtenir la version accélérée suivante (dite encore « time-lapse ») :
Après une nuit pluvieuse, le graphe avait déjà belle allure au lever de soleil :

Jouer sur le graphe
Sur la porte du bâtiment D a été placée cette affiche :
Les premiers joueurs ont été, calendrier oblige, les stagiaires SNT :

Ci-dessous, une joueuse de l’équipe des rouges est revenue à son point de départ : Sa distance à l’arrivée (à gauche sur la photo) est 2. Les deux autres joueurs rouges sont chacun à distance 1 d’un des sommets de l’arrivée. Par conséquent, la distance totale entre les joueurs rouges et leur arrivée est 1+1+2=4.

Quant aux autres joueurs, l’un d’eux est revenu au point de départ (tout à gauche) et il est lui aussi à distance 2 de son arrivée (à droite sur la photo). Les deux autres joueurs de son équipe sont respectivement à distance 1 (le joueur en vert est à distance 1 du sommet actuellement occupé par la joueuse en rouge) et à distance 2 (le joueur peu visible doit passer par le centre pour ensuite aller au milieu du côté droit du graphe). La somme de ces trois distances est 2+1+2=5 qui est plus grand que 4 : Actuellement ce sont les joueurs en rouge qui ont l’avantage sur l’autre équipe, et qui gagnent le jeu si la partie est interrompue à ce stade.
Vues aériennes
Le graphe, vu depuis le 3e étage du bâtiment A :
Voici quelques photos du graphe prises avec un drone :
Vu d’au-dessus
Plus haut
Encore plus haut
Toujours plus haut
Noter que le capteur GPS a fourni les coordonnées du graphe. Les voici sur GeoPortail :






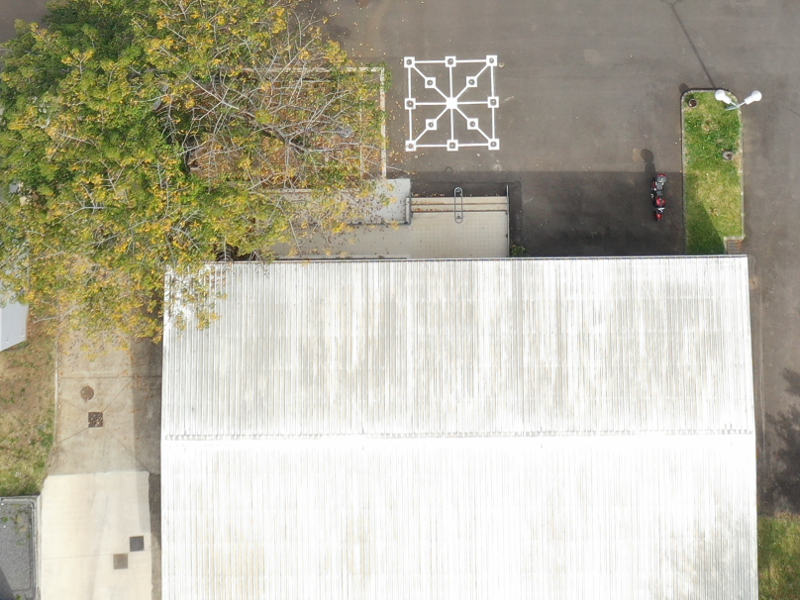










Commentaires