Ci-dessus, le curseur t représente le temps et l’affichage de la distance MN permet de conjecturer l’existence du minimum ainsi que la valeur de t permettant de l’atteindre.
Avec CaRMetal
CaRMetal possède tout ce qu’il faut pour lancer une animation. Pour commencer il faut créer une figure 3D :

La première chose à faire dans ce repère 3D est évidemment de placer les points A, B, C et D d’après leurs coordonnées. L’outil adéquat est le premier des outils de 3D :

Il faut choisir un point d"ancrage des coordonnées, qui seront ensuite partie intégrale de la figure (ici en haut à gauche). Ensuite on entre au clavier les coordonnées :
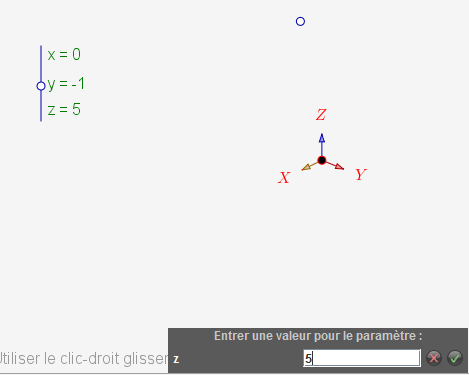
Il suffit de faire pareil avec B, C et D et de les renommer. Ensuite, pour mieux voir la figure, on trace les demi-droites AB et CD puisque t est le temps, donc a priori supposé positif (la figure est téléchargeable d’un clic droit) :
Alors en bougeant cette figure dans tous les sens, on constate que (AB) persiste à rester parallèle à (OI) ce qui se démontre en calculant les coordonnées du vecteur allant de A à B. Mais aussi que (CD) est dans un plan parallèle à (OJK) ce qui peut se montrer en constatant que puisque C et D ont même abscisse 11, ils sont tous les deux situés dans le plan d’équation x=11 qui est bel et bien parallèle à (OJK).
Pour la question suivante, On a tout intérêt à ne pas utiliser les coordonnées de E mais à les chercher : On calcule l’intersection de (AB) et P, en remplaçant x,y, et z par les coordonnées de M dans l’équation de P. C’est plus vite fait que dit, puisque comme l’équation de P est x=11, on n’a que l’abscisse à remplacer et celle-ci vaut t. On obtient alors t=11 qu’on remplace dans les coordonnées de Mt, on trouve alors que E=M11 a pour coordonnées (11,-1,5) comme annoncé dans l’énoncé.
Pour voir cela, on peut ajouter E dans la figure CaRMetal et dessiner le triangle CDE qui représente bien le plan P sans trop encombrer la figure. En faisant tourner celle-ci on voit l’orthogonalité entre P et (AB) :
La même manipulation de la figure permet aussi de voir que (AB) et (CD) sont non coplanaires. De toute manière, (AB) étant orthogonale à P, ne peut être parallèle à (CD), et l’intersection E n’est pas alignée avec C et D, comme on peut le montrer en résolvant le système
- 0,8t=-1
- 1+0,6t=5
qui aurait donné la valeur du paramètre pour laquelle N serait en E.
Pour la suite, il est nécessaire de synchroniser le mouvement de N sur celui de M, le temps devant s’écouler à la même vitesse sur les droites (AB) et (CD). Par conséquent, on va animer automatiquement t et définir les coordonnées de M et N en fonction de t.
On crée une expression t avec l’outil adéquat :

On la met en mode curseur et on fixe sa borne inférieure à 0 :

Ensuite on crée les points M et N en utilisant t dans les coordonnées :

Après, il ne reste plus qu’à choisir l’outil d’animation :

Celui-dit demande quel est le point que l’on souhaite animer, et en choisissant t au lieu d’un point, l’animation se fait toute seule, comme sur la figure CaRMetal obtenue, que l’on peut télécharger en cliquant sur la copie d’écran ci-dessous :
Avec GeoGebra 3D
Pour commencer, vu qu’on est en 3D, il faut afficher la fenêtre 3D de GeoGebra :
Après quelques réductions, l’image ressemble à ceci :
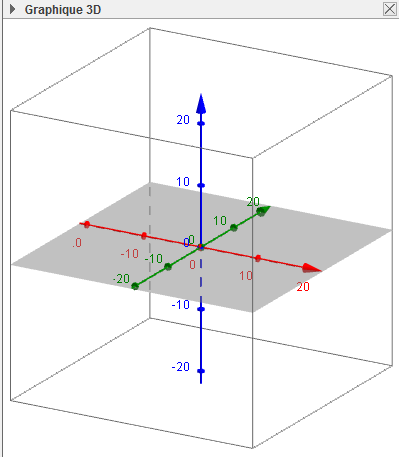
Après on entre au clavier
A=(0,-1,5)
B=(2,-1,5)
C=(11,0,1)
D=(11,4,4)Difficile d’imaginer plus simple !
Ensuite, l’outil demi-droite permet de compléter la figure. Il faut donc quelques secondes pour obtenir ce dessin en anaglyphe, qui, regardé avec des lunettes rouge-cyan, montre immédiatement
- que (AB) est parallèle à (Ox)
- que (AB) et (CD) ne sont pas coplanaires
- que (CD) est parallèle à (Oyz), donc orthogonale à (AB) :
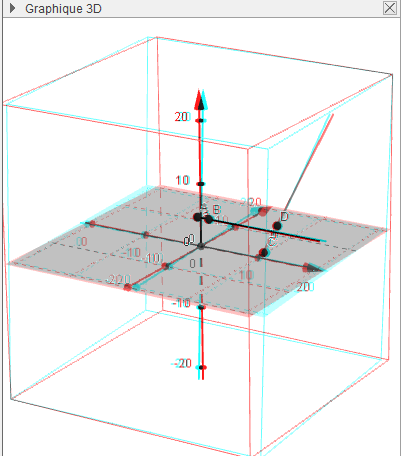
Une difficulté rencontrée par les élèves pour cette épreuve de bac est qu’ils ne sont pas nécessairement habitués à identifier x=11 comme une équation de plan. Avec GeoGebra c’est facile à voir, il suffit d’écrire x=11 dans la fenêtre d’entrée :

L’inclusion de (CD) dans ce plan saute aux yeux munis de lunettes anachromes. La suite est un vrai bonheur : On sélectionne l’outil « intersection » puis la demi-droite AB et le plan, et un point apparaît, qui s’appelle E et a pour coordonnées (11,-1,5). C’est à se demander si l’énoncé n’a pas été conçu avec l’aide de GeoGebra... Par contre, on a du mal à voir le point E, qui est clair et partiellement caché par le plan :
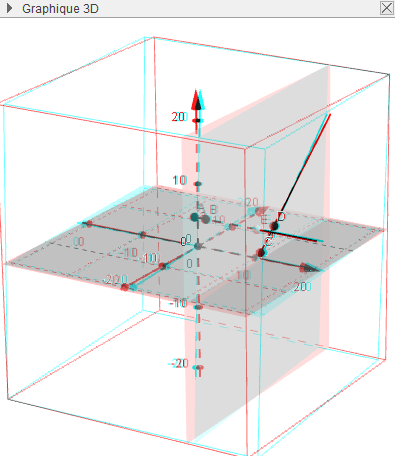
La suite doit se faire dans la figure 2D : Créer le curseur t, lui donner pour bornes 0 et 12. Ensuite, retour à la fenêtre 3D, et on écrit
M=(t,-1,5)
N=(11,0.8*t,1+0.6*t)
Distance[M,N]Ensuite, en actionnant le curseur t, on cherche à minimiser la distance, en regardant l’affichage. Ceci répond à la question. Mais pour mieux voir, on peut représenter cette distance par la sphère de diamètre MN :
MilieuCentre[M,N]
Sphère[F, M]Après il est conseillé de cacher les plans parce que sinon on ne voit pas grand-chose. La suite est un jeu en 3D : Bouger t pour rendre la sphère la plus petite possible :
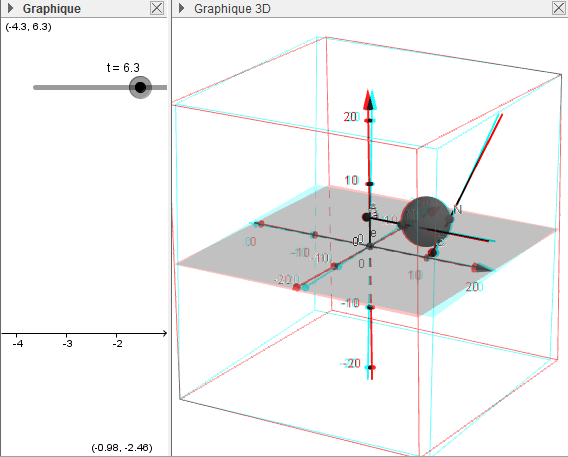
Après avoir joué un peu, le bonheur revient avec
Minimiser[d,t]
qui crée un nombre de valeur 6,3. Le bonheur...
Après avoir renommé t autrement (pour libérer la variable t), un petit séjour par la fenêtre de calcul formel permet de rapidement démontrer le résultat coinjecturé :

DGPad
La construction de la figure est immédiate aussi avec DGPad, grâce à son outil « calculatrice » :
- Avec la macro « repère 3D », créer un repère de centre O (qui se crée là où on clique) dont il est bon de renommer les points I, J et K pour rester le plus proche possible de l’énoncé ;
- On ouvre la calculatrice et on entre A=[0,-1,5] et des choses analogues pour B, C et D.
- On clique sur A, on choisit l’outil demi-droite et on sélectionne B ; idem pour C et D.
- Pour calculer les coordonnées des vecteurs (questions 1a et 1b), on crée des expressions B-A (on voit à ses coordonnées qu’elle est colinéaire à OI) et D-C (on voit à ses coordonnées qu’elle est perpendiculaire à OI) ;
- On entre E=[11,-1,5] puis on représente le plan P=(CDE) par le cercle circonscrit à CDE (on voit alors que CD est une corde du cercle et que (AB) lui est perpendiculaire en E) ;
- On crée un curseur t allant de 0 à 12 ;
- On crée les expressions [t,-1,5] et [11,0.8*t,1+0.6*t] que l’on met en mode point et que l’on nomme M et N ;
- La macro distance 3D, appliquée à M et N, fournit une expression qui finit la construction (cependant ça ne fait pas de mal de dessiner aussi le segment [MN]).
La figure obtenue est celle-ci :
Conclusion de ce petit banc d’essai [1] :
- L’entrée des coordonnées sous CaRMetal se faisant par des boîtes de dialogue, on risque moins de se tromper. Cependant, l’ergonomie de GeoGebra et DGPad est plus « directe », surtout avec DGPad sur tablette, grâce à son clavier virtuel « spécial maths ».
- Le calcul formel de GeoGebra est appréciable dans ce genre de problème. La fonction Minimiser est vraiment impressionnante !
- Le dessin d’un plan dans GeoGebra alourdit considérablement la figure, parce que le plan étant infini, est représenté par un gros rectangle qui encombre la figure. Le triangle de CaRMetal et le cercle de DGPad sont plus légers.
- Les curseurs de CaRMetal et DGPad ne sont que des cas particuliers d’expressions générales, c’est une souplesse appréciable aussi ;
- Les possibilités d’animation de CaRMetal et GeoGebra sont à l’origine de cet article, puisque celui-ci parle de cinématique...
- Le mode anaglyphe de GeoGebra est vraiment génial !
- La possibilité de construire une sphère dans GeoGebra a permis de transformer un exercice de bac en un jeu vidéo, merci à ses créateurs !
- DGPad permet de facilement mettre une figure en ligne, c’est pourquoi il a été choisi pour illustrer cet article.



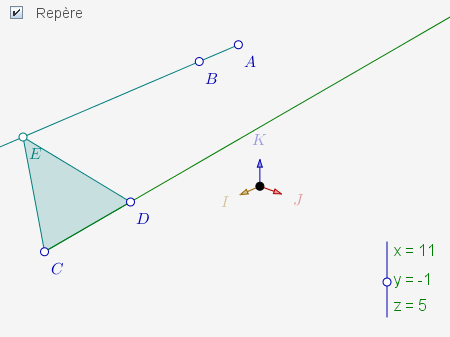

Commentaires