Triangle de Pascal
Pour commencer, on peut assez facilement dessiner un triangle de Pascal dans le transcript :
-
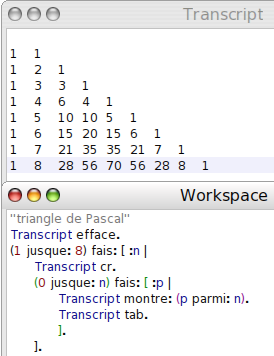
crva à la ligne (nécessaire après avoir incrémenté n, puisque dans ce cas la ligne de n est terminée) -
tabva à la prochaine position « tabulaire » du transcript ; c’est ce qui permet d’écrire des colonnes verticales. Il faut dédoubler le nombre de « tab » pour écrire le triangle de Pascal à partir de la ligne 9.
Loi binomiale
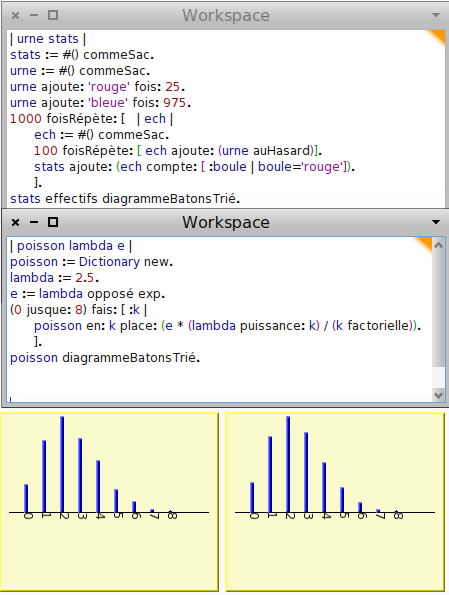
Donc, pour simuler une variable aléatoire suivant une loi binomiale de paramètres 12 et 0,6 par exemple, on simule le tirage de 12 boules (avec remise) dans une urne contenant 60 % de boules rouges, et on compte le nombre de boules rouges obtenues parmi les 12.
Ici, l’urne contient 100 boules au total (c’est un choix parmi bien d’autres) et le tirage avec remise se fait dans un sac appelé ech initialement vide, mais dans lequel on ajoute à 12 reprises une boule tirée au hasard dans l’urne. Une fois que le comptage des boules rouges dans l’échantillon est effectué, on ajoute la variable binomiale dans un autre sac appelé stats sur lequel on peut à la fin faire des statistiques comme par exemple dessiner son diagramme en bâtons :
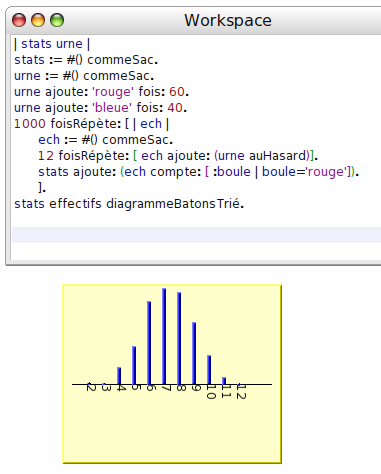
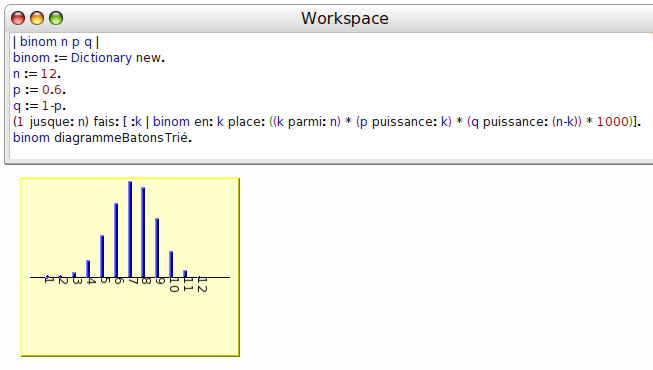
Pour comparer avec la formule théorique, on doit multiplier celle-ci par un grand nombre (ici 1000) pour éviter que des erreurs d’arrondi perturbent l’affichage :
extensions
Pour simuler une variable aléatoire de Poisson, il suffit donc de simuler une variable binomiale de paramètre n grand, et de paramètre p égal au quotient du paramètre de la loi de Poisson par n. Par exemple pour simuler une variable de Poisson de paramètre 2,5 on peut utiliser le fait que 100×0,025=2,5 et simuler une variable binomiale de paramètres 100 et 0,025 :
C’est long mais précis (le diagramme en bâtons théorique est à droite).
Pour simuler une variable aléatoire suivant une loi normale centrée réduite, on peut simuler une variable binomiale de paramètres n assez grand et p=0,5 puis centrer et réduire le résultat. À partir d’une variable X normale centrée réduite, on peut simuler une normale d’espérance m et d’écart-type s en multipliant X par s puis en ajoutant m au résultat.
Par exemple, pour simuler une variable normale de paramètres 16 et 2,5 on peut faire ainsi (très rapide) :
Loi géométrique
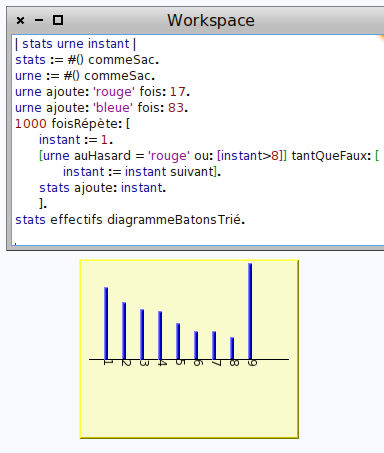
Pour simuler une variable aléatoire suivant une loi géométrique, on peut utiliser sa définition temporelle : Compter à combien on doit s’y prendre pour avoir une boule rouge ; par exemple, une variable géométrique de paramètre 0,17 peut se simuler en mettant 17 boules rouges dans une urne en contenant 100 en tout, et en comptant combien de fois on doit en reprendre une avant d’avoir une rouge :
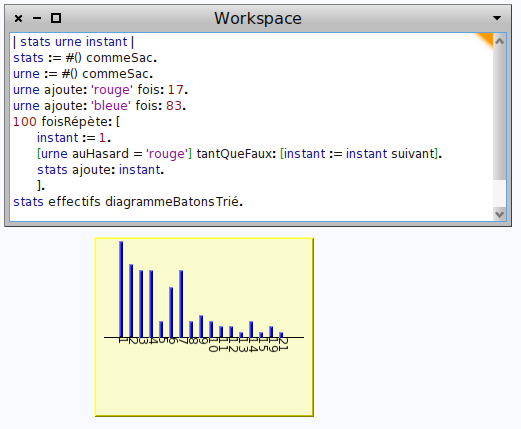
La variable aléatoire s’appelle instant. Il faut peu de modification pour avoir une variable suivant une loi géométrique tronquée :
extension
Pour simuler une variable aléatoire suivant une loi exponentielle, on peut simuler une variable géométrique de paramètre petit ; par exemple, pour simuler une variable exponentielle de paramètre 2,5 on peut utiliser le fait que 100×0,025=2,5 et mettre 25 boules rouges dans une urne en contenant 1000 au total : Le centième de la variable géométrique simulée suit approximativement une loi exponentielle de paramètre 0,01×0,025=2,5 :
Un cours rapide sur la loi binomiale a été fait en terminale STI2D, le récit est ci-dessous :
|
Commentaires