Une machine de Post sans programme est manipulable en ligne ici. D’autres sont là.
Le codage suivant a été choisi :
| Symbole | Uspensky | Post | explication |
| ✔️ | V | marking the box he is in | faire en sorte que l’index montre une graine |
| ❌ | ξ | erasing the mark in the box he is in | faire en sorte que l’index montre une case vide |
| ☛ | ⇒ | moving to the box on his right | déplacer l’index vers la case à droite |
| ☚ | ⇐ | moving to the box on his left | déplacer l’index vers la case à gauche |
| 👁️ | ? | determining whether the box he is in, is marked | regarder si l’index montre une graine ou une case vide et déplacer le pion en conséquence |
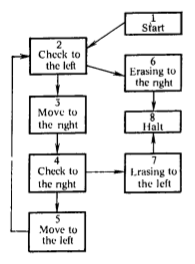
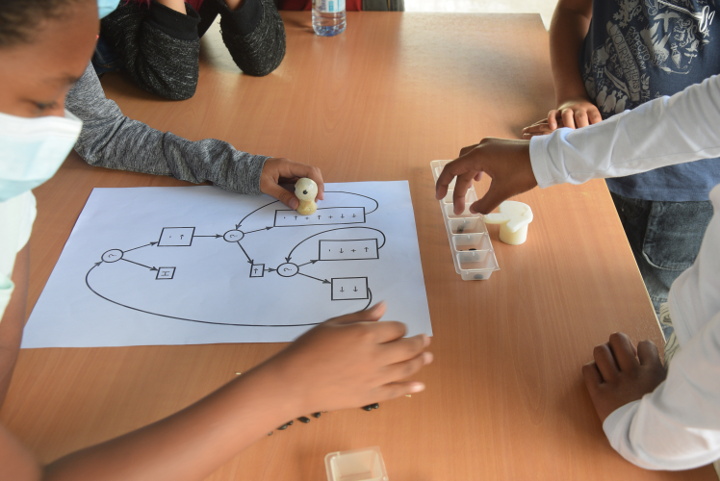
Il faut 3 élèves pour exécuter un programme :
- l’un se charge de déplacer le pion sur le graphe, et dire aux deux autres ce que le pion dit de faire,
- un autre est chargé de l’index et de ses déplacements,
- le troisième est chargé des graines dans les cases (transport de graines entre les cases et la réserve de graines), et notamment dira au premier élève s’il y a une graine dans la case, ou non.
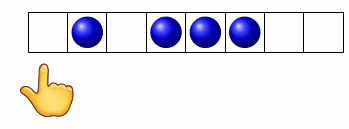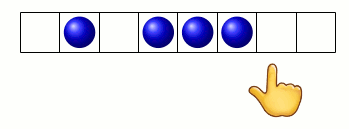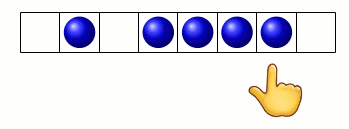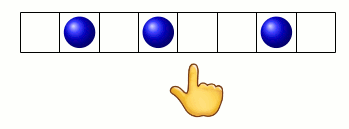
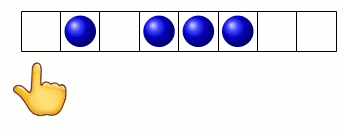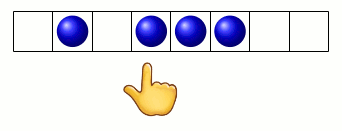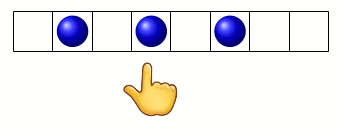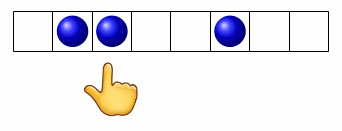
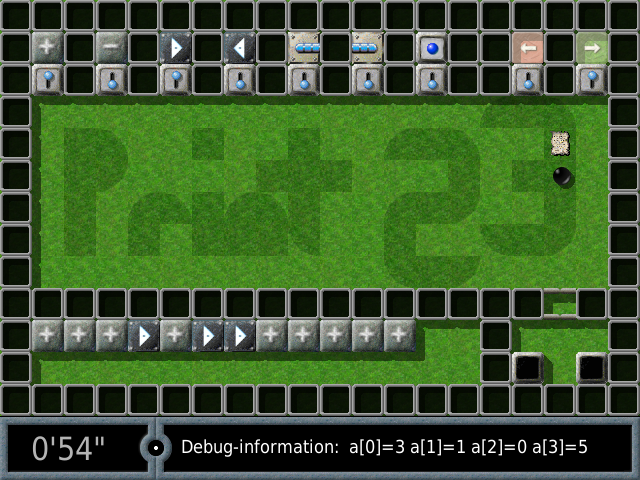
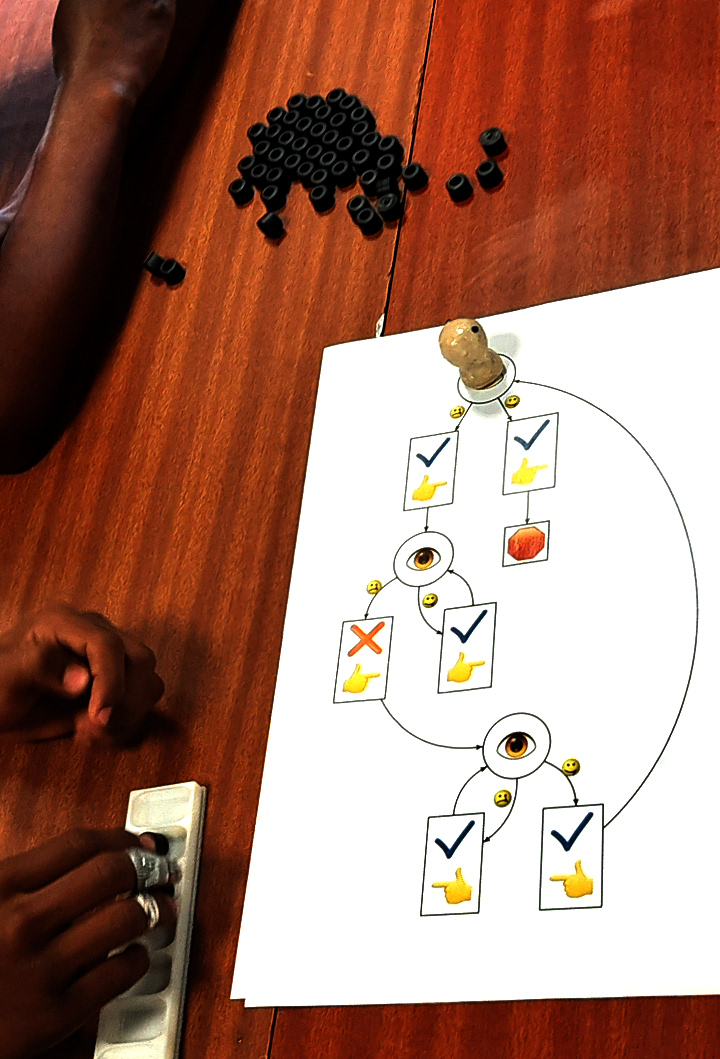
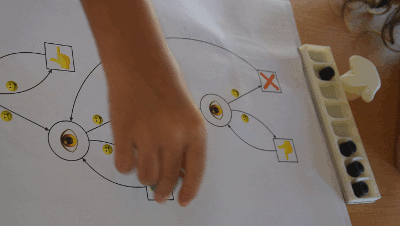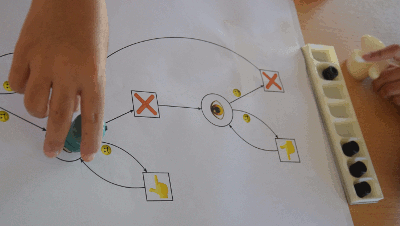
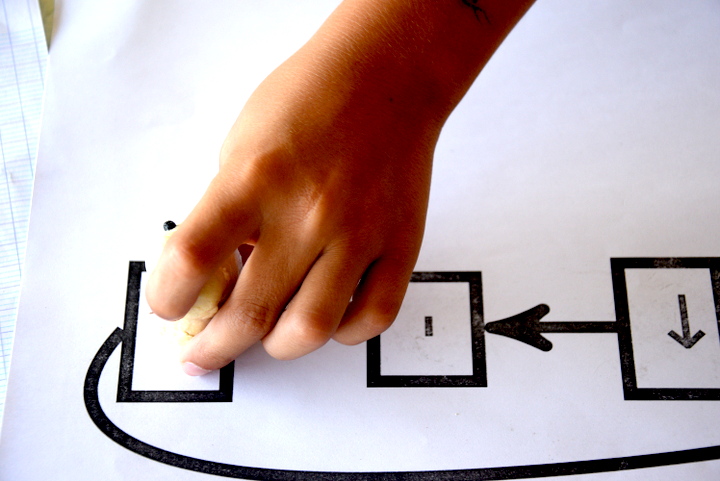
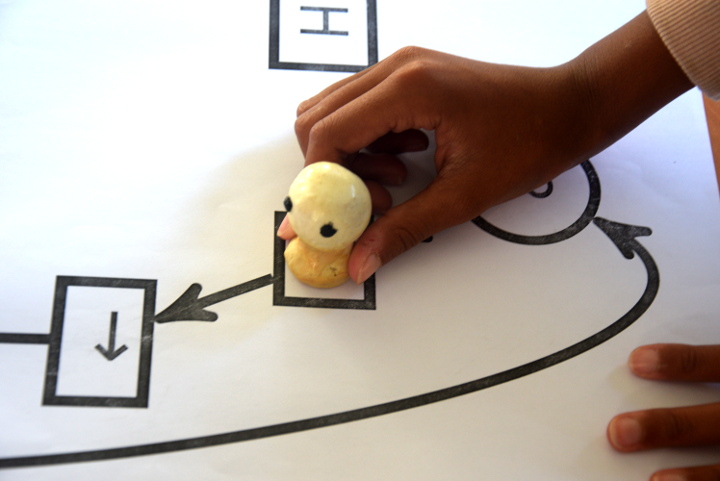
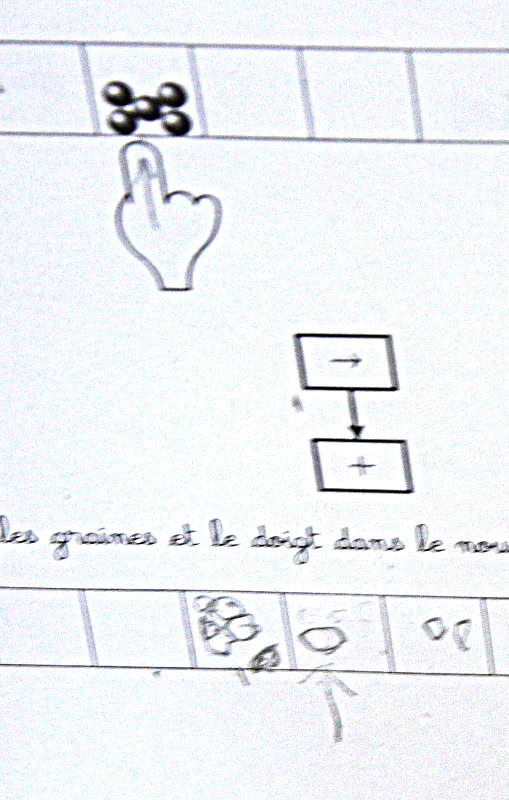
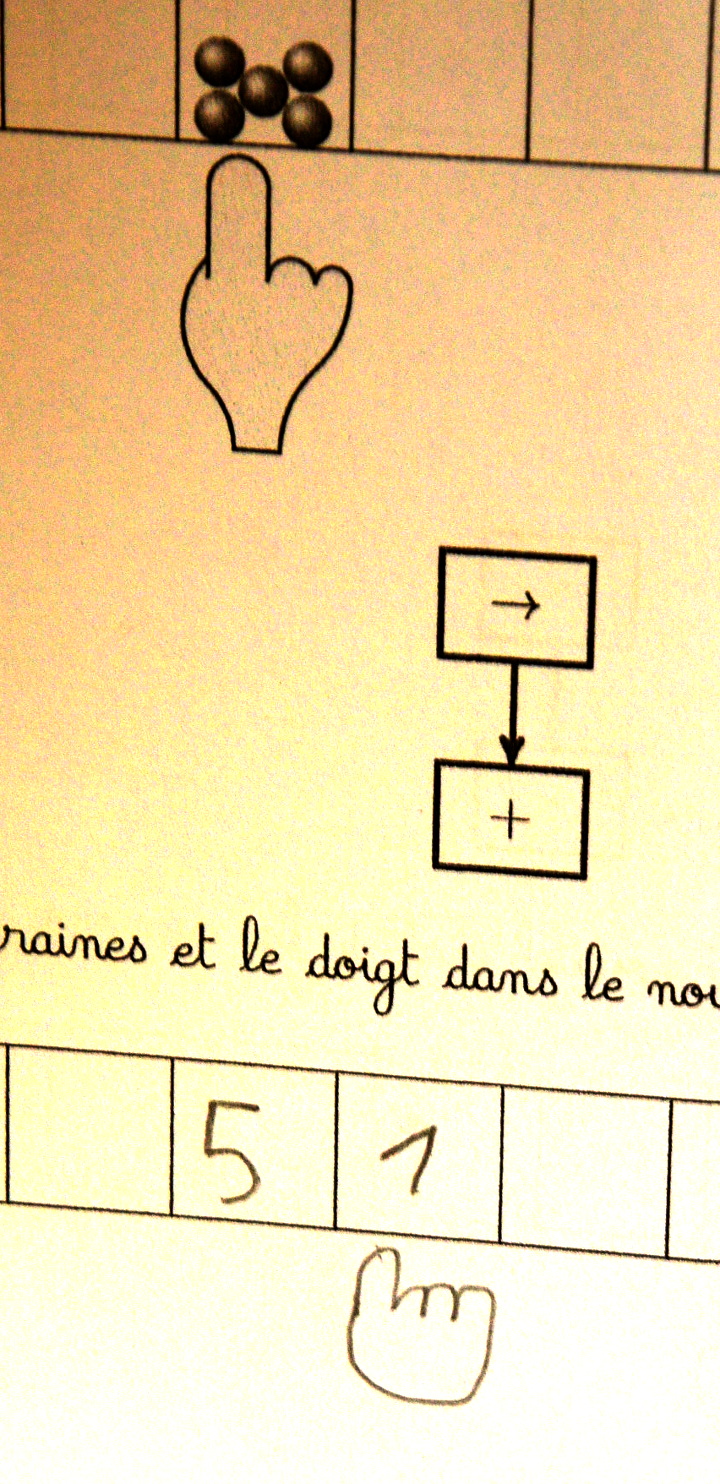
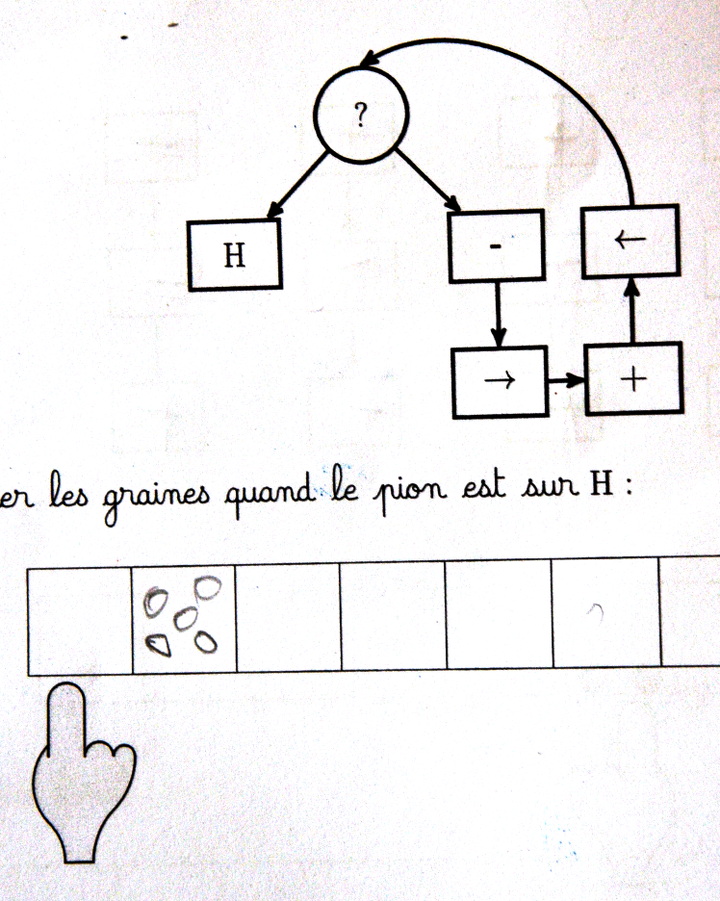
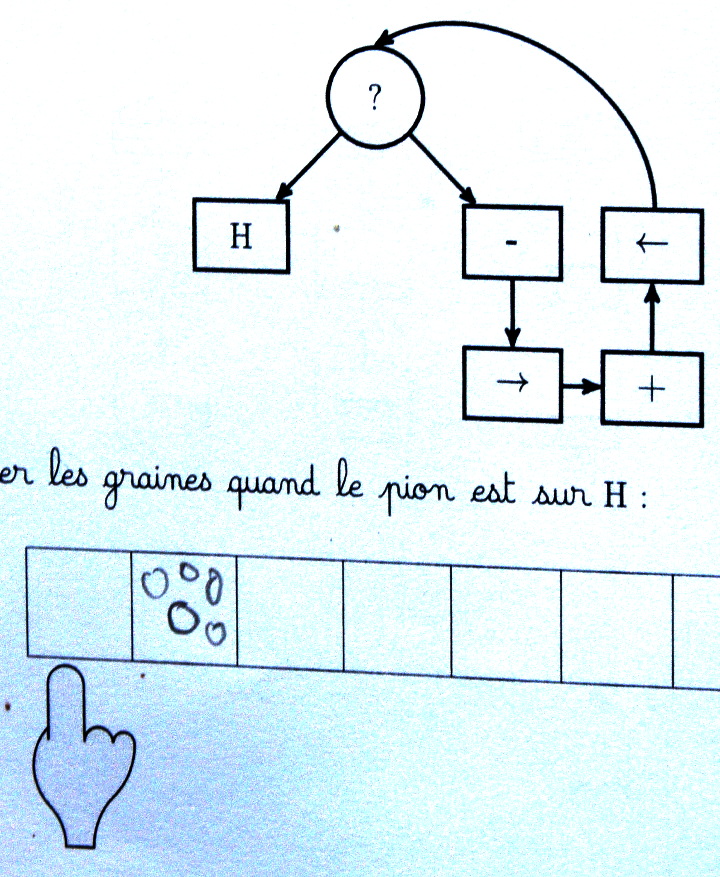
Par exemple, le pion étant posé sur un œil, le gestionnaire du graphe demande si l’index montre une graine. C’est le cas :

donc le pion part vers la droite du graphe (marquée par le smiley) :
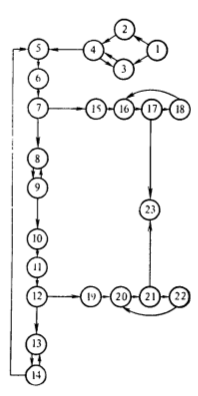
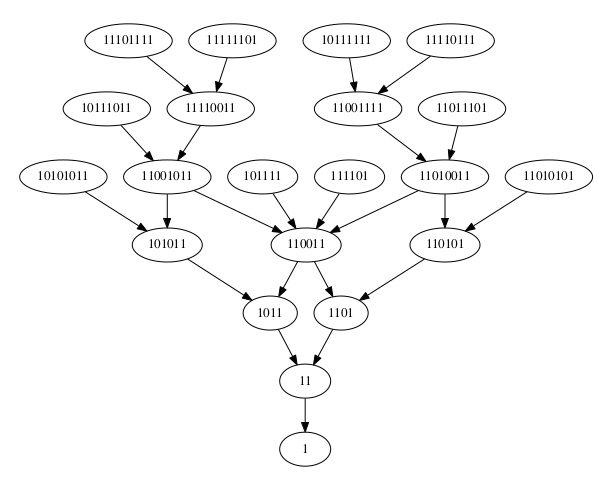
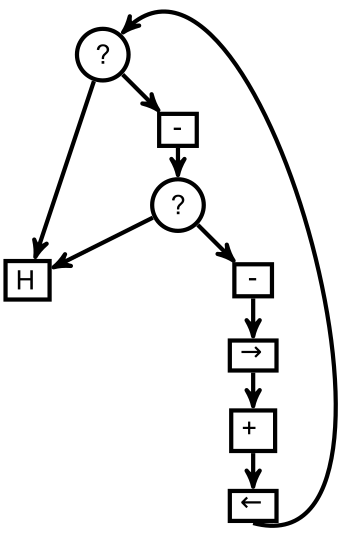
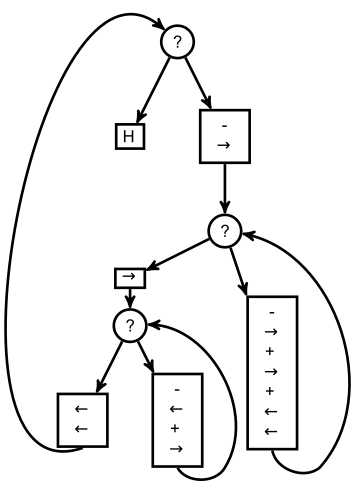
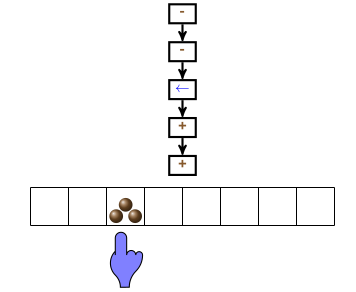
L’exemple ci-dessus est en fait un castor affairé :


Fête de la science
Les machines de Post et à registres ont été testées durant la fête de la science 2021 avec la caravane de l’IREMI.
lycée Rontaunay
La première date a été le lycée Rontaunay. Les graines utilisées sont en caoutchouc qui supporte bien le gel hydroalcoolique :


Les élèves trouvent un moyen à la fois esthétique et ergonomique pour stocker les graines de la réserve de graine :

L’animation des jeux a été assurée par des élèves du lycée, qui ont suivi une rapide formation en début de matinée puis ont initié leurs camarades aux machines de Post.
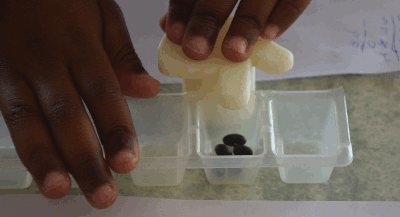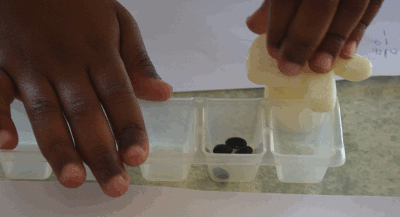
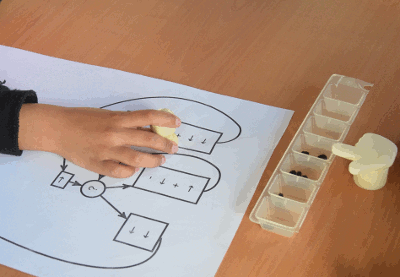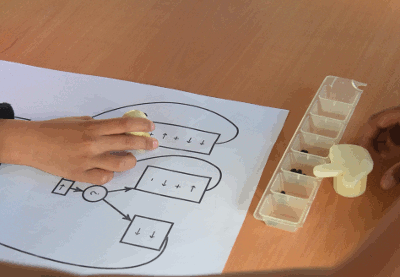
Voici un programme en cours d’exécution, on voit le déplacement de l’index vers une case occupée, puis une hésitation (l’instruction est de placer une graine alors qu’il y en a déjà une) puis un nouveau déplacement de l’index :
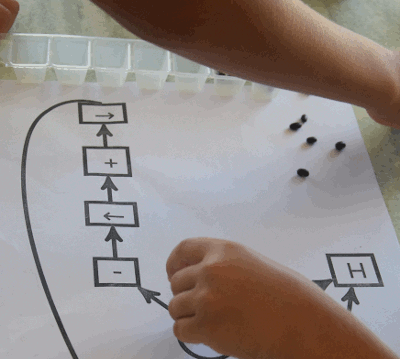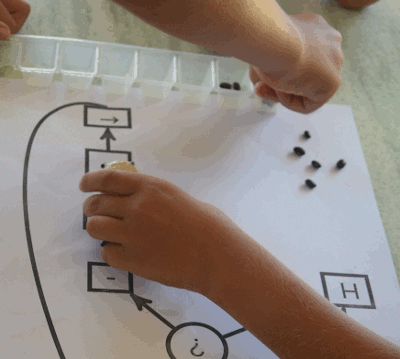
Un castor affairé s’apprête à construire un motif grâce à ce programme :
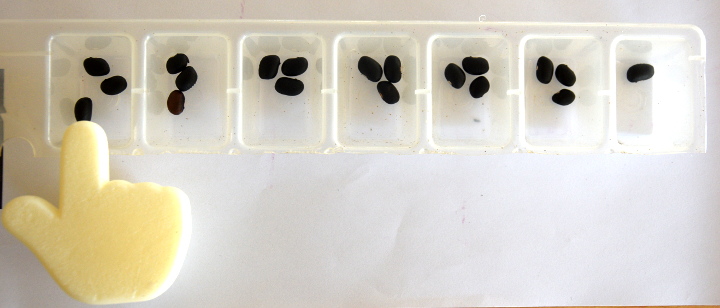
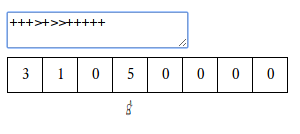
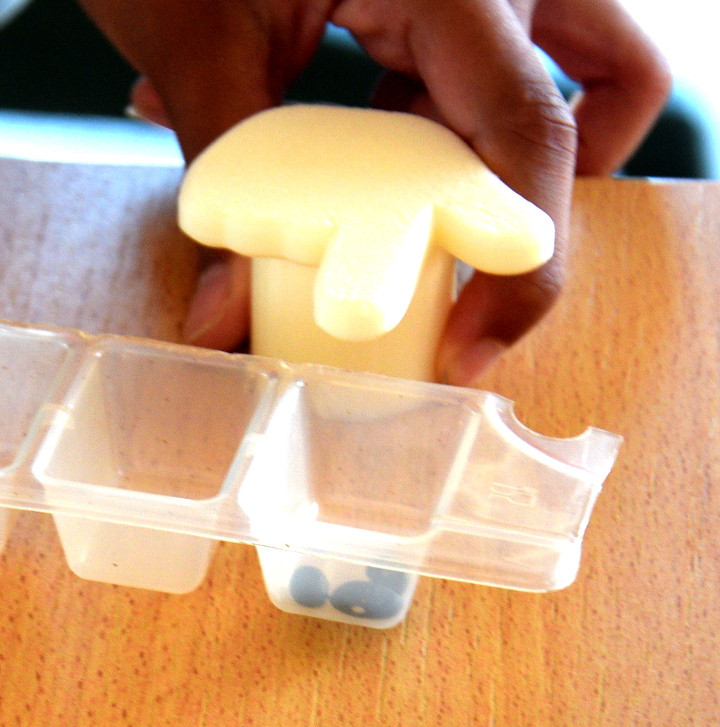
Un élève vient de poser l’addition 3+3 (3 graines de chaque côté de la case vide) et s’apprête à lancer le programme d’addition sur la machine de Post :

Les machines à registre semblent avoir eu la préférence des élèves animateurs de l’activité. Celle-ci a fait l’objet d’un rappel sur les fonctions :
En effet, il n’y a de graines que dans la première case avant le début du calcul, et que dans la seconde case à la fin du calcul. Le nombre final de graines est donc fonction du nombre initial de graines. Le but du jeu, dans ce cas, était d’essayer de deviner quelle est la fonction. L’exécution répétée du programme permet de construire le tableau de valeurs suivant :
| nombre initial de graines | nombre final de graines |
| 0 | 0 |
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 2 |
| 6 | 3 |
Iris Hoarau
À l’école Iris Hoarau, la plupart des élèves ayant semé des graines avec la machine de Post (en fait, à registres) étaient en CE2. Mais une classe de CM1 est passée et elle a eu droit à la version binaire.


Les élèves de CE2 ont eu droit à des manipulations sur machines à registres.


Un élève a essayé de généraliser la machine en y ajoutant deux autres opérations :
Ne sachant pas par quoi il convenait de multiplier ou diviser, il s’est arrêté là, mais un pas a été fait vers une réinvention du langage de programmation FRACTRAN...
Claire Hénou
Les élèves de CE2, CM1 et CM2 de l’école de la Plaine-des-Palmistes ont eux aussi eu majoritairement droit à la version registres.

Les élèves ne pouvant (ou voulant) assister à l’activité ont été chargés de rédiger un reportage sur l’activité. En voici un :
Aujourd’hui ils sont en train de jouer à la machine de Post. On a des cases et des pions et dans chaque case il y a un signe. Alors on a des haricots. On les met dans des trous. Il y a une main...




Analyse
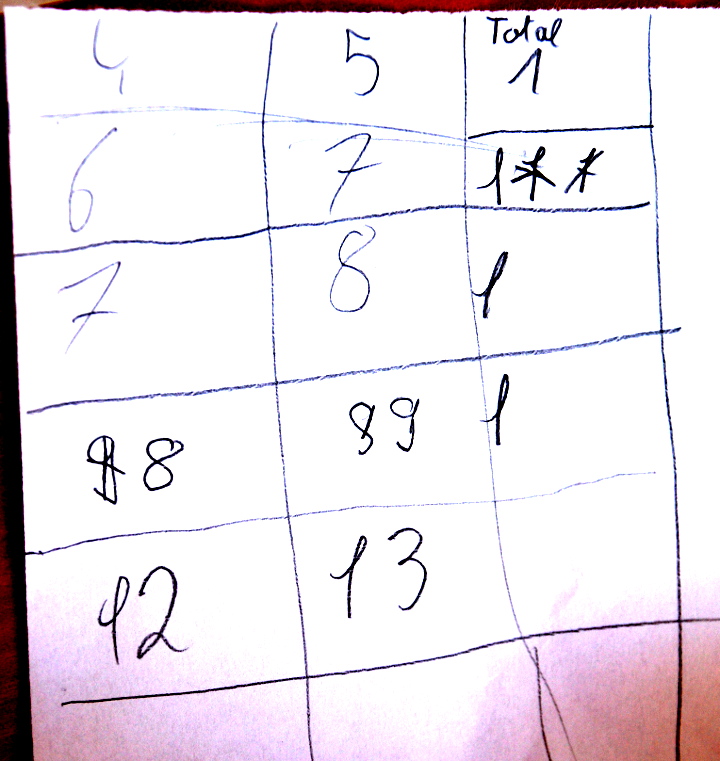
Ce fut l’occasion de voir aussi comment se trompaient les élèves, notamment avec la version registres. Leurs erreurs ont été analysées avec la programmation Python :
Cycle 2
Les machines à registres ont été présentées dans 3 classes de l’école Aristide Briand au début de l’année 2022. L’accueil par les enseignants et aussi par les élèves, donne envie de continuer l’expérience en cycle 2.
Programmes
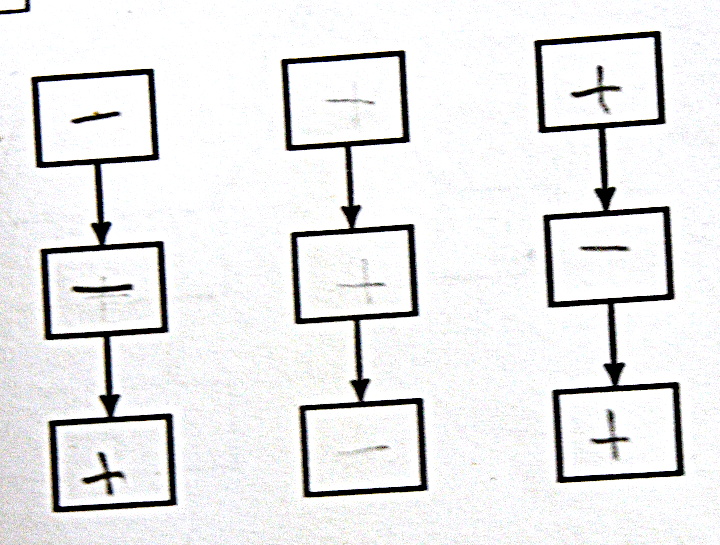
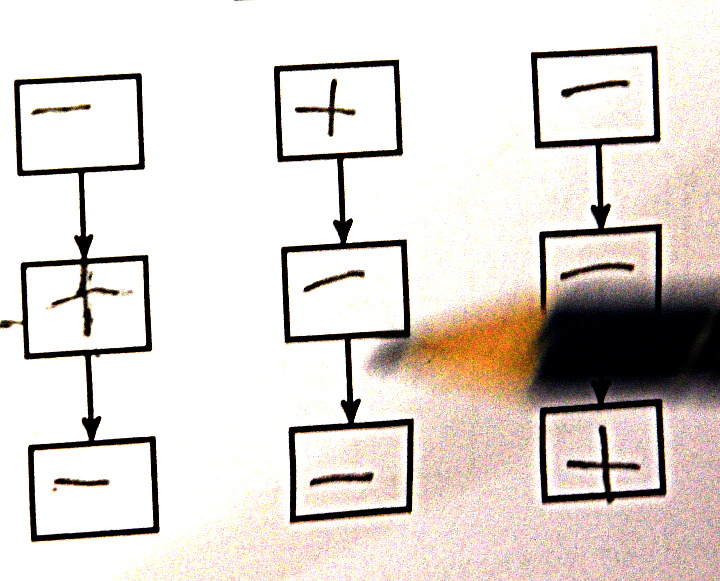
On constate
- une nette tendance à utiliser chaque instruction une et une seule fois,
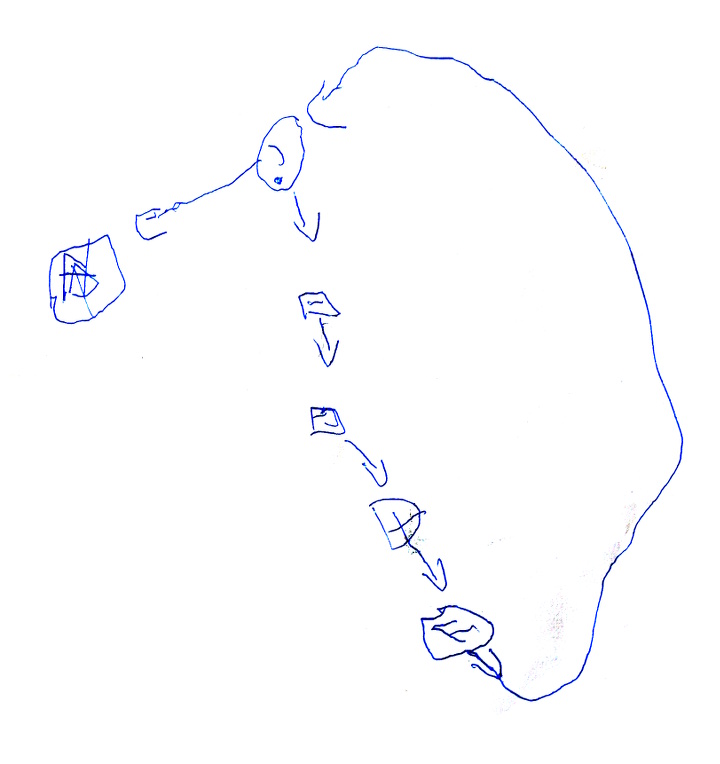
- des difficultés à dessiner (et probablement à voir) les pointes de flèches,
- une tendance à croiser les flèches,
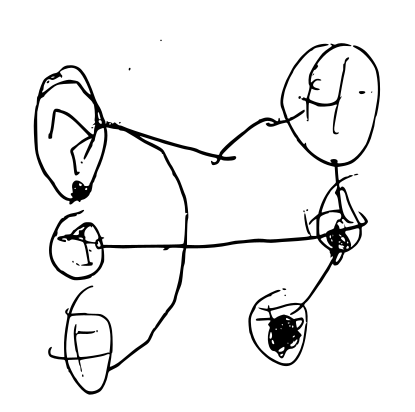
- une certaine ressemblance avec les graphes tracés l’année dernière (en GS) par les mêmes élèves (visibles dans cet article) :
Deux algorithmes originaux ont cependant été produits, on les présente dans les deux onglets suivants.
Alyassa
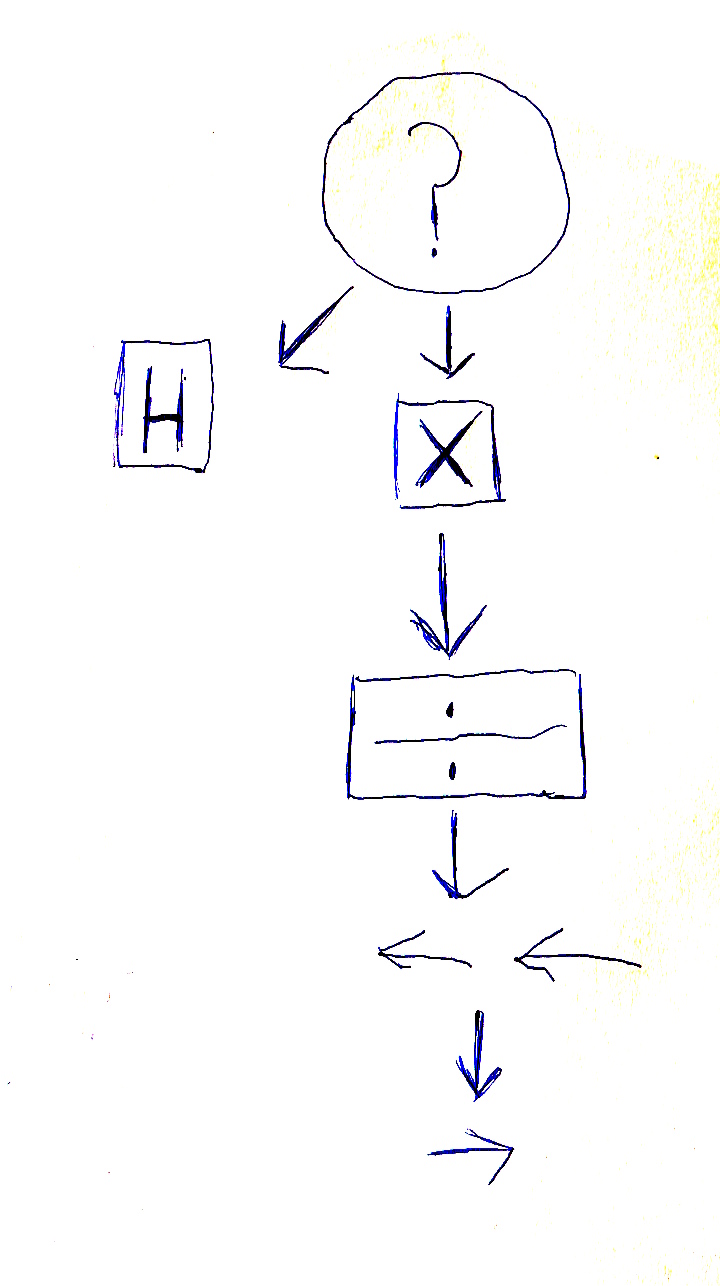
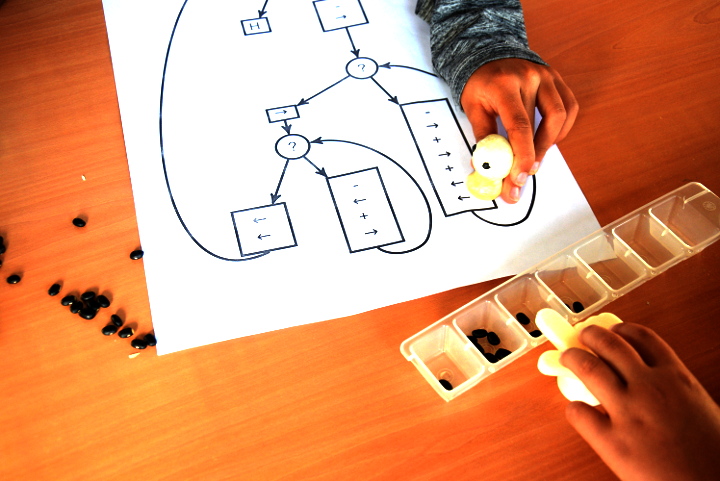
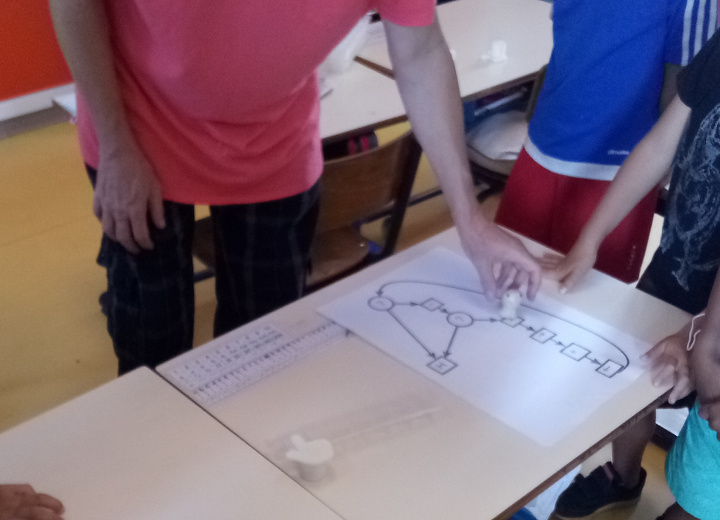
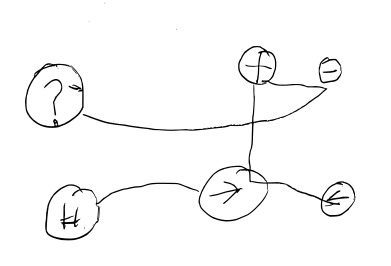
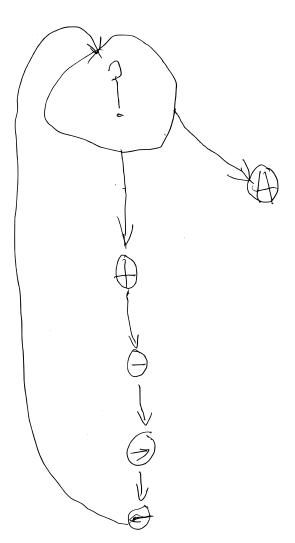
On voit ici l’histoire se construire. Voici le brouillon d’Alyassa :
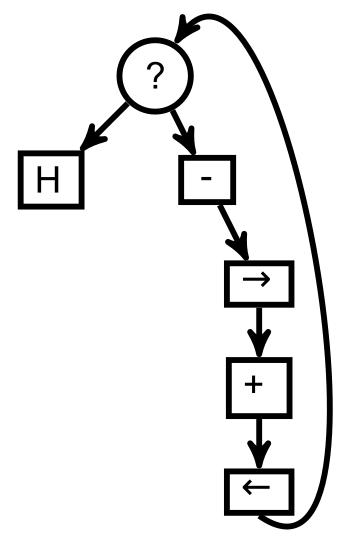
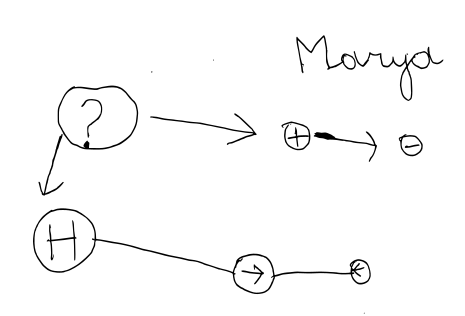
Puis il a décidé de refaire ce graphe de manière plus visible :
Ce programme est non seulement presque (la case testée n’est pas la bonne) correct, mais aussi original. Que fait-il ? La partie « ?H » signifie qu’on fait le reste tant qu’il y a des graines dans la case présente. Le reste, est décomposable en trois blocs d’instructions :
- Deux « + » qui font ajouter deux graines dans la case présente,
- un « ←-→ » qui fait enlever une graine dans la case voisine de gauche,
- deux autres « + » qui font ajouter deux graines à nouveau.
Le ←-→ est une action par conjugaison (on conjugue le « - » par une translation « → » ce qui a pour effet d’appliquer le « - » à côté) de la théorie des groupes. Par ailleurs, les trois blocs d’instruction « commutent » ce qui veut dire que ce programme a exactement le même effet que
- Deux « + » qui font ajouter deux graines dans la case présente,
- deux autres « + » qui font ajouter deux graines à nouveau,
- un « ←-→ » qui fait enlever une graine dans la case voisine de gauche.
et donc que
- Quatre « + » qui font ajouter quatre graines dans la case présente,
- un « ←-→ » qui fait enlever une graine dans la case voisine de gauche.
En dehors de l’erreur sur la case à vérifier, il s’agit donc d’un programme de quadruplement.
Lucy
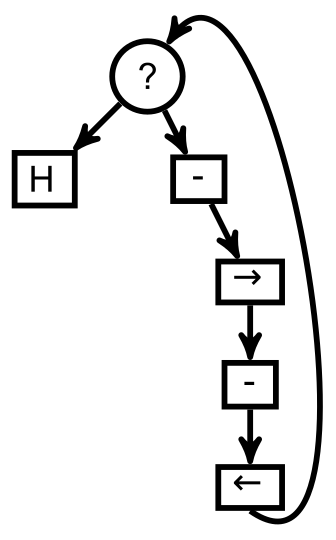
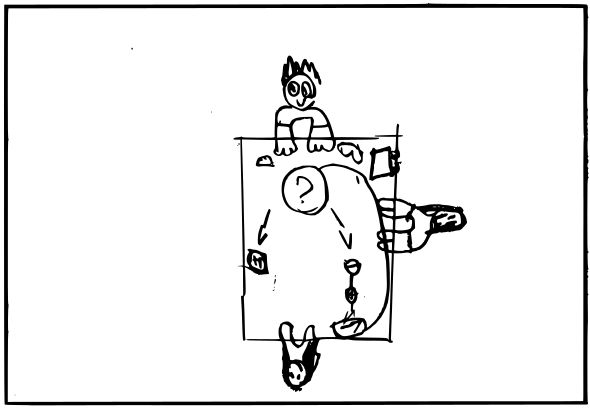
Le programme de Lucy lui aussi, est original :
Il y a deux interprétations possibles, selon que Lucy a fait, ou non, une erreur de latéralisation. Si elle a échangé la gauche et la droite, le programme s’arrête lorsque le doigt pointe une case vide. Sinon, on sème une graine puis on va à la case suivante et on enlève une graine. La condition d’arrêt du programme est donc que le doigt est arrivé sur une case où il n’y avait, initialement, qu’une graine. L’algorithme de Lucy vise donc à ajouter une graine à toutes les cases consécutives qui en contenaient déjà plusieurs. Par exemple, en commençant sur ce tableau
| 3 | 2 | 5 | 4 | 1 | 2 | 3 | 0 |
il s’arrête sur
| 4 | 3 | 6 | 5 | 0 | 2 | 3 | 0 |
Mais si par contre Lucy n’a pas échangé la gauche et la droite, son programme reste intéressant et original. Il s’arrête à la première case qui ne contient pas une graine unique, et tant que le doigt est devant une case contenant une graine, il l’enlève puis la remet. Par exemple sur ce tableau
| 0 | 1 | 1 | 1 | 1 | 3 | 1 | 1 |
il donne
| 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
mais le doigt devant la case à 2 graines.
CP b
La classe de CP b de la même école a eu droit à l’activité le jeudi 10 février 2022 :
L’idée discutée à la fin de la séance est intéressante à expérimenter un jour de beau temps :
- le graphe serait tracé (à la craie par exemple) par terre,
- le rôle de Monsieur Post serait interprété par un.e élève,
- le doigt serait incarné par un.e autre élève,
- les instructions seraient dessinées sur des étiquettes que Monsieur Post lirait à voix haute,
- les graines seraient remplacées par des ballons,
- la mémoire serait matérialisée par un alignement de bacs.
CE2
Un livret a été préparé pour la visite d’une classe de CE 2 (cliquer sur l’image pour avoir le pdf) :
Il comprend 15 fiches d’exercices à mener éventuellement sans la machine de Post. Ce livret a été distribué aux RMC de l’académie le lundi 9 mai, avec cette présentation :
Pendant ce temps, une classe de CE 2 (école Aristide Briand) a pu manipuler des machines de Post pour faire les fiches des pages 2 à 13.
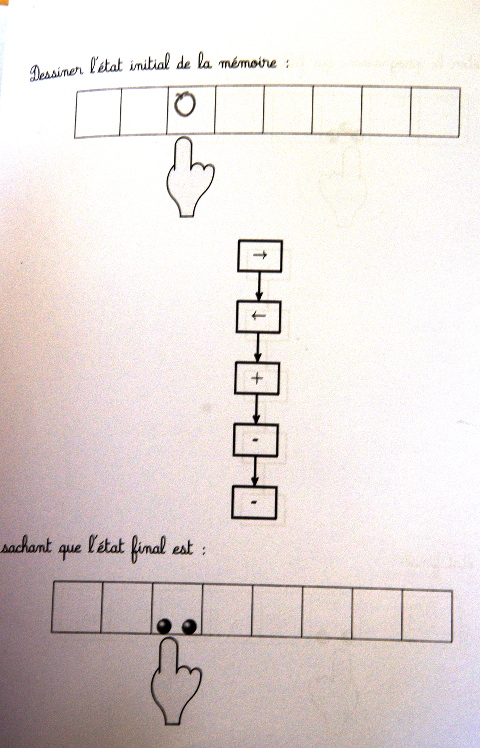
page 2
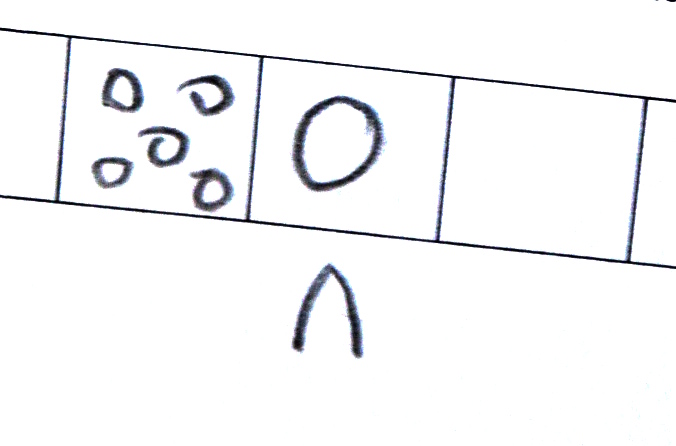
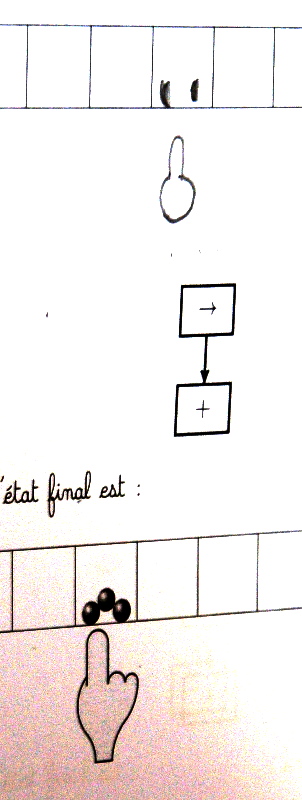
Exemple de recherche d’état final selon la modélisation de Vergnaud : on connaît
- l’état initial (1 graine)
- la transformation (ajout de 2 graines)
et on demande l’état final :

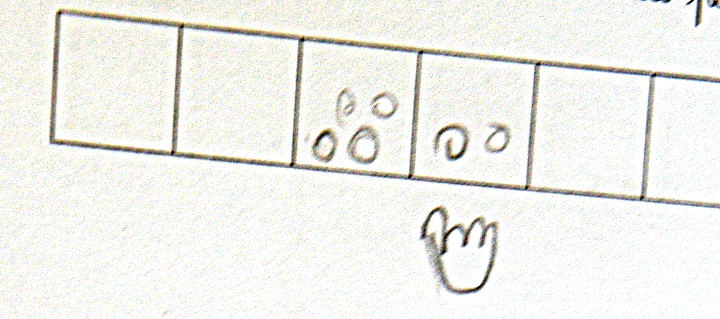
Parmi les (rares) erreurs constatées, on voit
- le dessin des seules graines ajoutées (et pas de l’ancienne graine)
- le dessin des graines sur l’état initial au lieu (ou en plus) de l’état final.
On remarque une tendance à dessiner les 3 graines en triangle, ce qui n’est pas le cas sur un dé ou un domino.
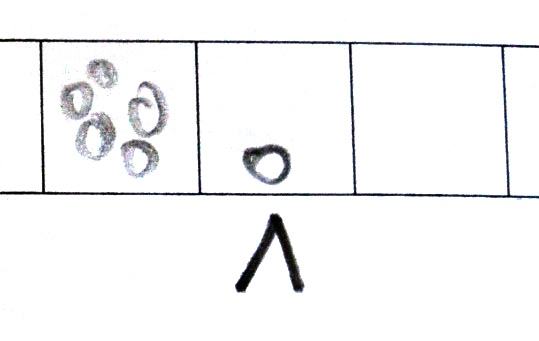
page 3
Une soustraction cette fois-ci. Certains élèves recopient l’état initial puis barrent les graines récoltées, ce qui évoque le dessin des nombres négatifs dans TiPont974 :

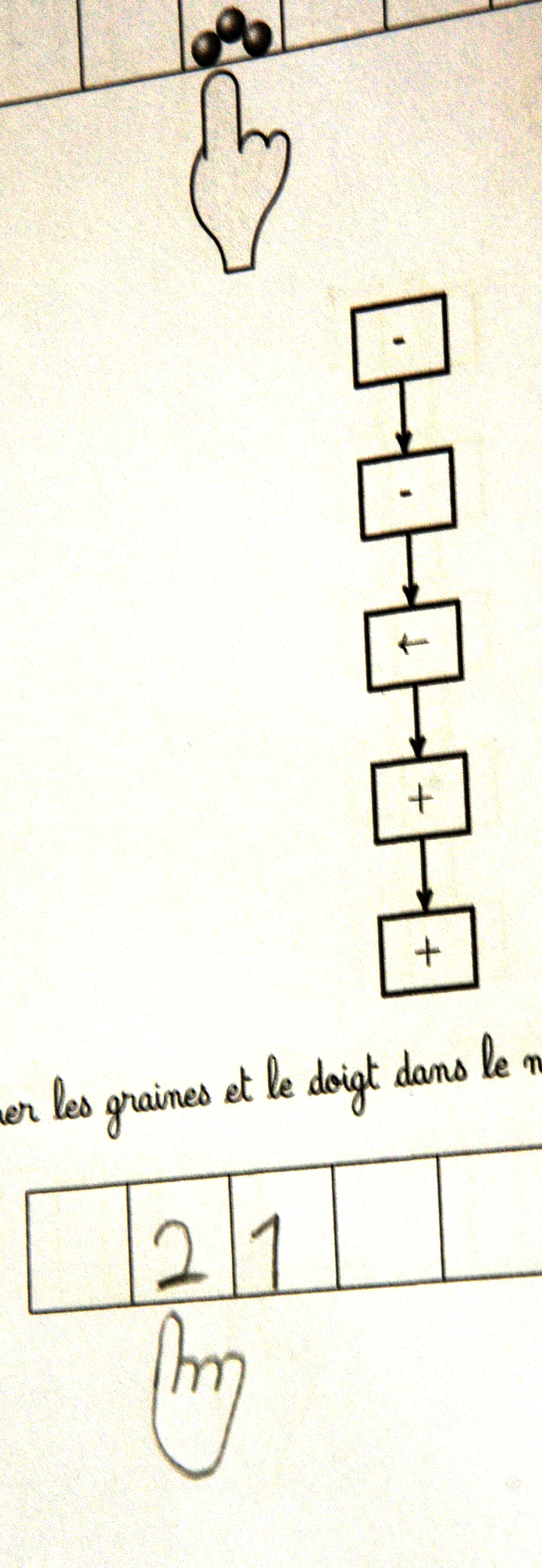
page 4
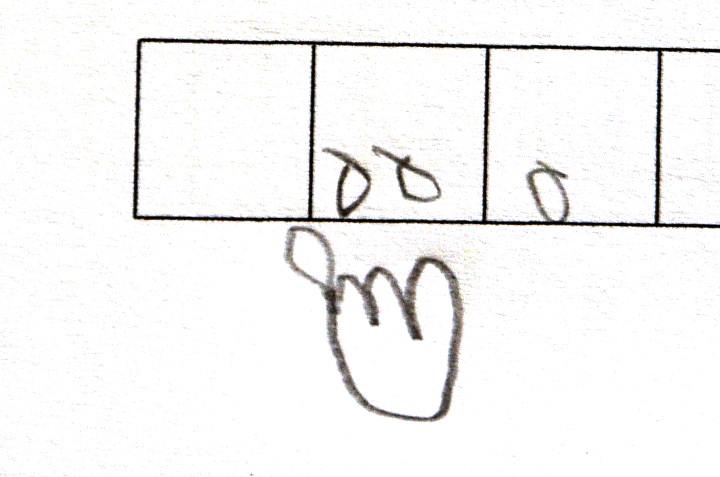
Comme le doigt bouge avant le semis, celui-ci ne s’effectue pas sur la case de départ mais sur celle d’à côté :
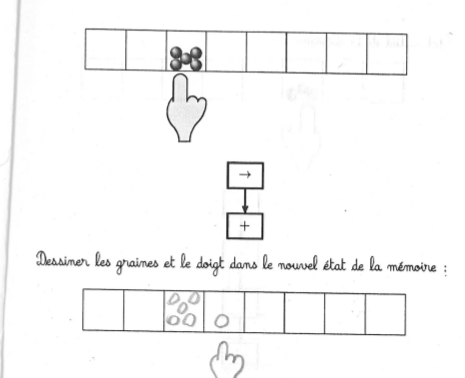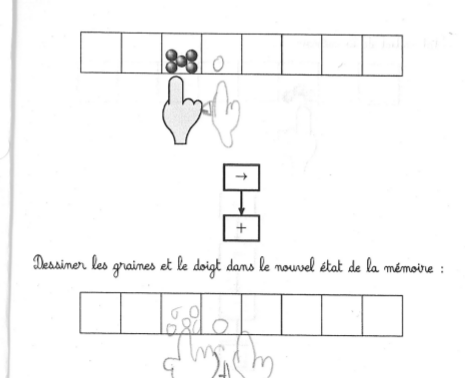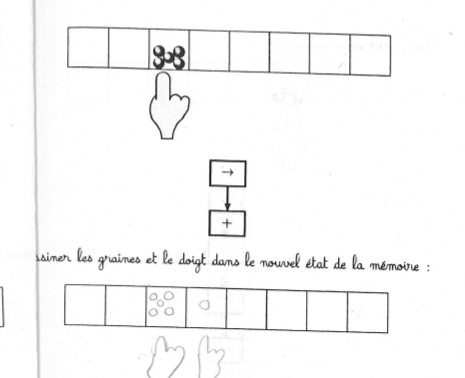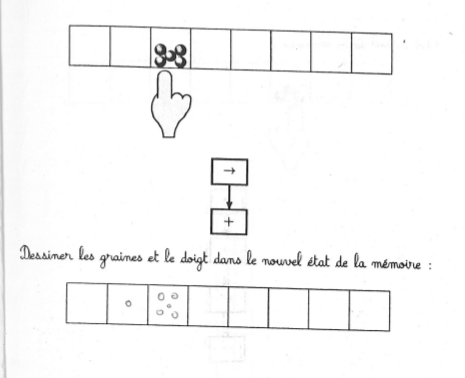
La graine semée à gauche est une conséquence probable de la disposition des élèves face à face ce qui fait que certains voyaient la machine de Post à l’envers.
Les 6 graines pourraient venir d’une inversion de l’ordre d’exécution des instructions. Mais cela n’explique pas que parfois les 6 graines sont dans la case de droite.
On voit aussi parfois une volonté de dessiner non seulement la position finale du doigt mais aussi toutes les positions intermédiaires.
page 5
Un agriculteur ne fait pas que semer et récolter, il faut aussi qu’il sache piloter son tracteur :

On voit une tendance à dessiner non seulement la position finale du doigt mais aussi les positions intermédiaires.
Le doigt n’a pas toujours bougé durant l’exécution du programme.
page 6
Taux de réussite élevé :
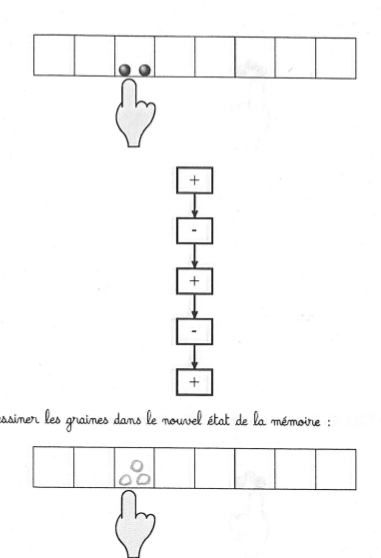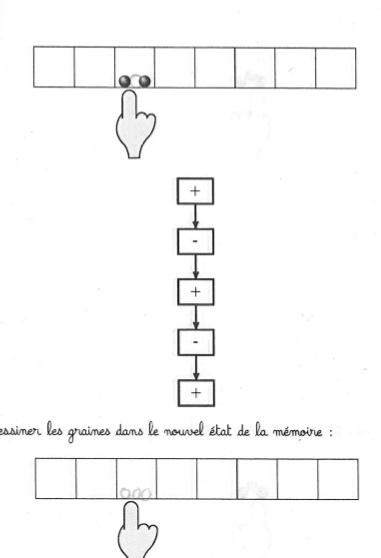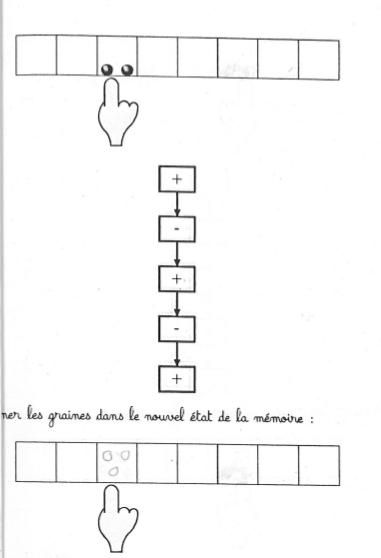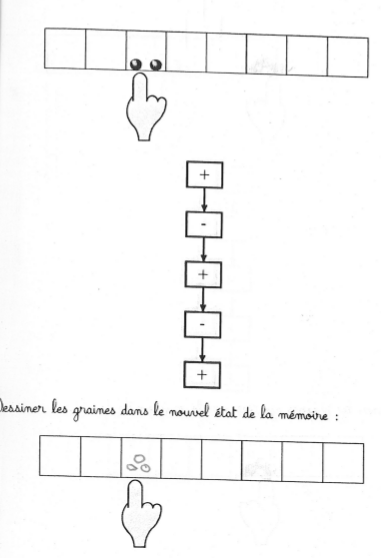
On peut comparer les stratégies utilisées pour dessiner les graines.
page 7
Taux de réussite important (les élèves ont bien compris qu’il fallait ajouter 3 graines, quitte à barrer la 4e qui est ensuite enlevée) :
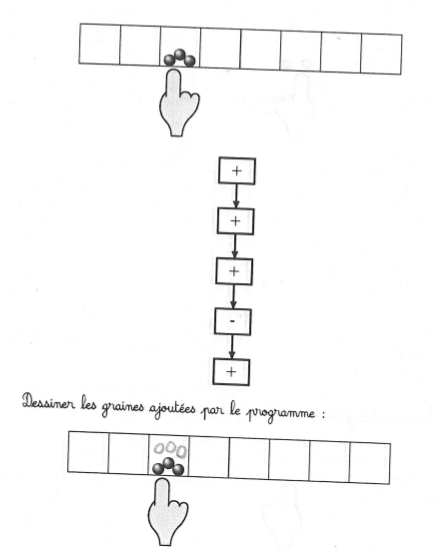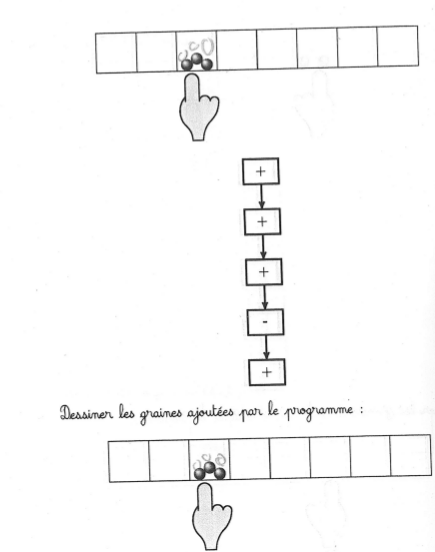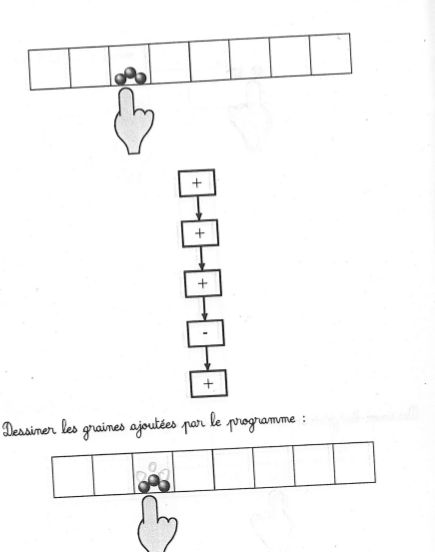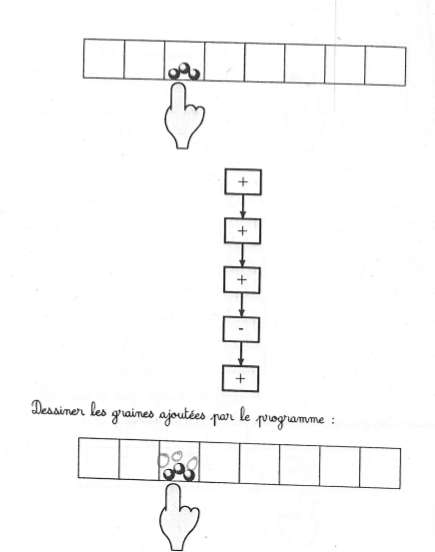
On remarque que souvent pour dessiner les 3 graines supplémentaires on recopie celles qui sont déjà présentes.
page 8
L’algorithme se résume à un transfert de deux graines, de la case actuelle vers sa voisine de gauche :
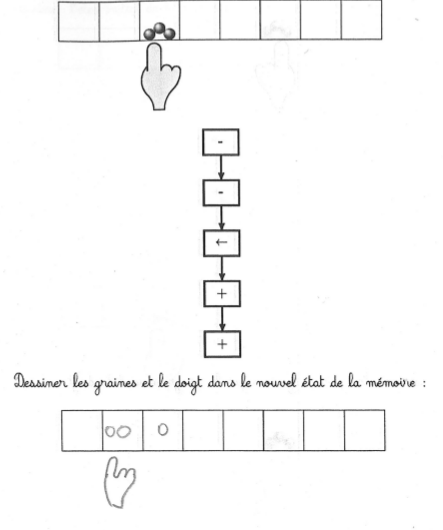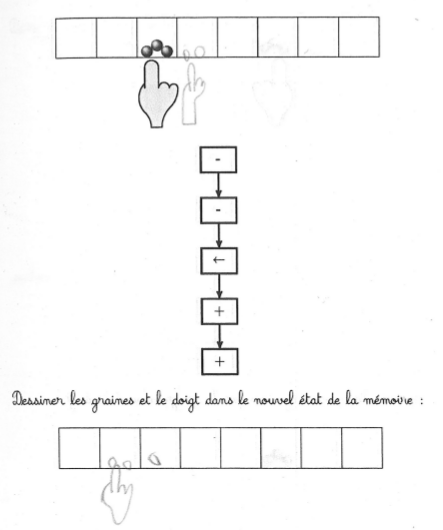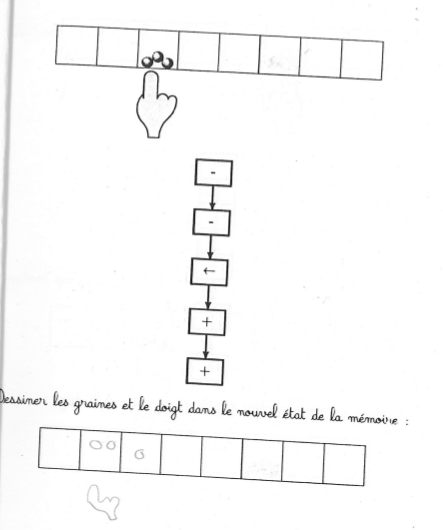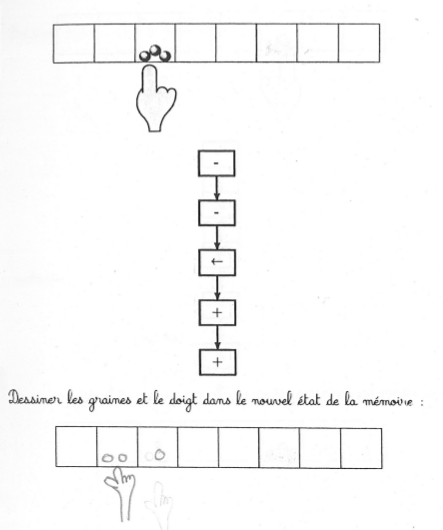
Le taux de réussite est élevé mais
- la récolte initiale des 2 graines (avant de les resemer) a parfois été oubliée
- elle a aussi été remplacée par un semis
- trois graines ont été récoltées au lieu de 2.
Le dessin à l’envers vient d’une élève qui faisait face à sa coéquipière et elle a dessiné l’état final de la machine telle qu’elle le voyait (voir onglet suivant).
page 9
Les élèves se faisant face avec la machine de Post entre eux, celle-ci n’était tournée correctement que pour l’un d’entre eux. Ce qui peut expliquer que parfois les deux graines aient été semées à gauche plutôt qu’à droite :

Parfois le mouvement du doigt est oublié et les graines sont semées dans la case de départ. Mais plus surprenant il arrive que les 5 graines au total soient recopiées dans la case de droite, comme si les 3 graines avaient été transférées, en plus des semis.
page 10
Un problème de type recherche d’état initial à la Vergnaud (le doigt ne bouge pas) :
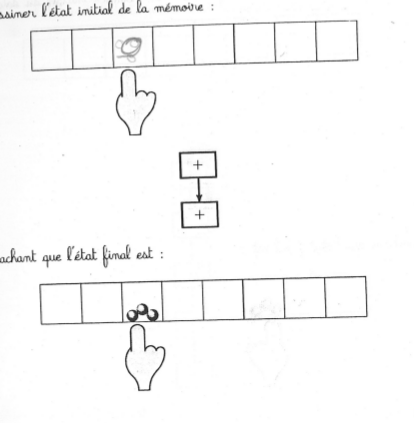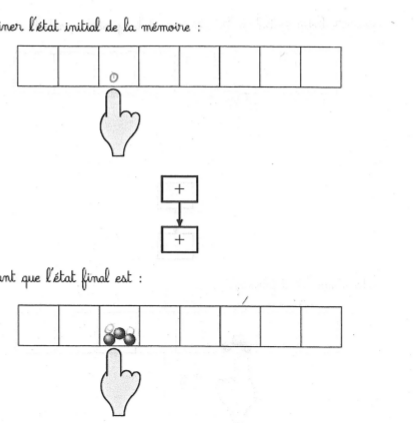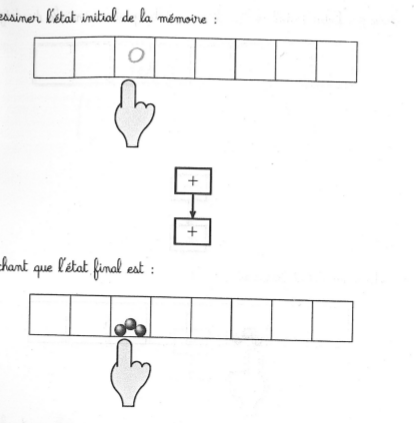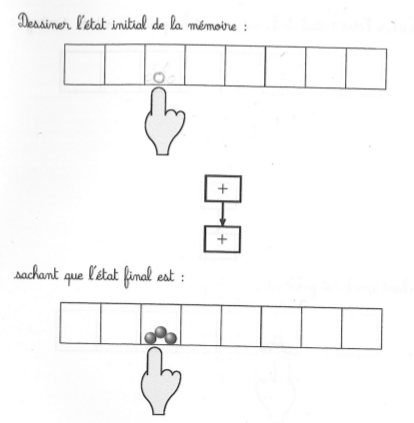
Certains élèves ont d’abord cherché à appliquer la transformation (une double incrémentation) à l’état final puis se sont ravisés, et n’ont pas toujours utilisé la gomme pour revenir à l’énoncé.
On voit aussi, à deux reprises, une confusion entre état et transformation ce qui aboutit à deux graines au lieu d’une dans la case de l’état initial.
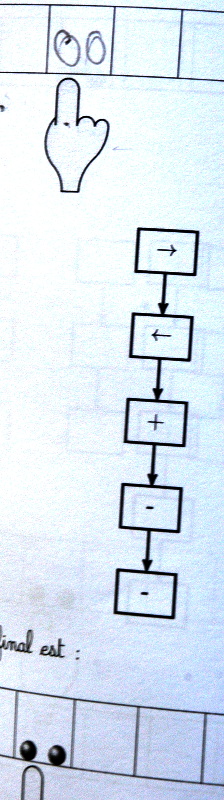
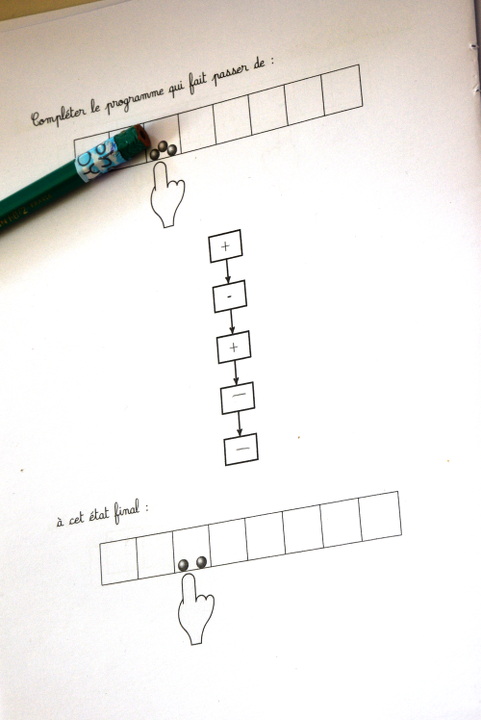
page 11
Exercice complexe même s’il n’y a que deux instructions dans le programme. Il semble y avoir assez souvent une confusion entre le mouvement du doigt et les semis et récoltes. En fait il y a une tendance à seulement permuter les instructions élémentaires sans les modifier :
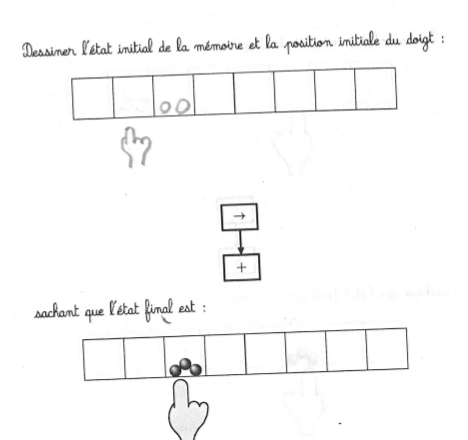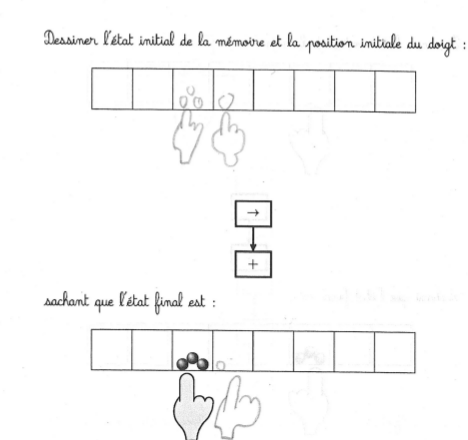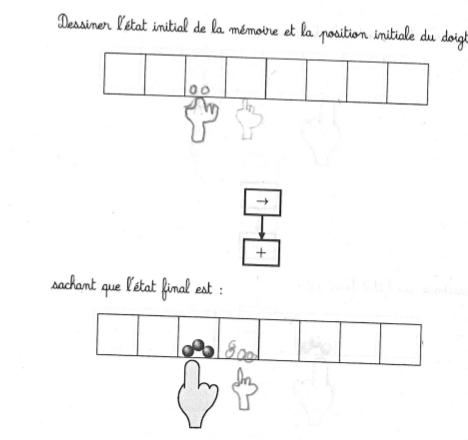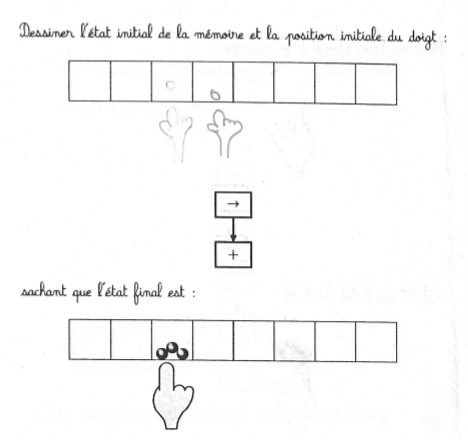
Essayer d’appliquer les opérations à l’état final est assez fréquent sur cette activité. Les deux seules élèves qui ont donné une réponse correcte, se sont trompées sur la première case : elles ont ajouté deux graines alors qu’après en avoir enlevé une, la case était vide.
page 12
La machine de Post n’aide pas beaucoup pour cet exercice complexe, car même si on a deviné l’état initial, après vérification, on a oublié les détails. Il faudrait a minima une deuxième machine pour mémoriser l’état initial. D’ailleurs l’état final a parfois été utilisé comme brouillon.
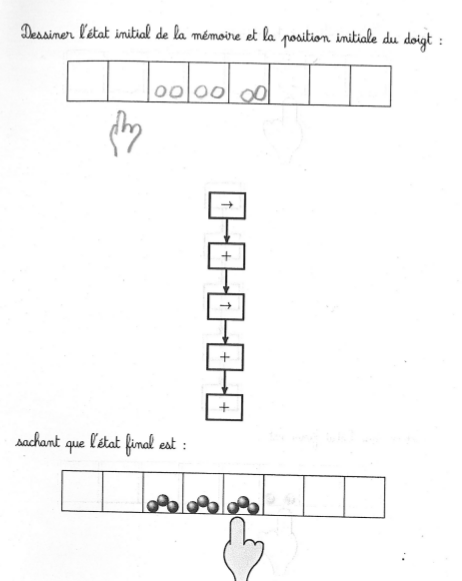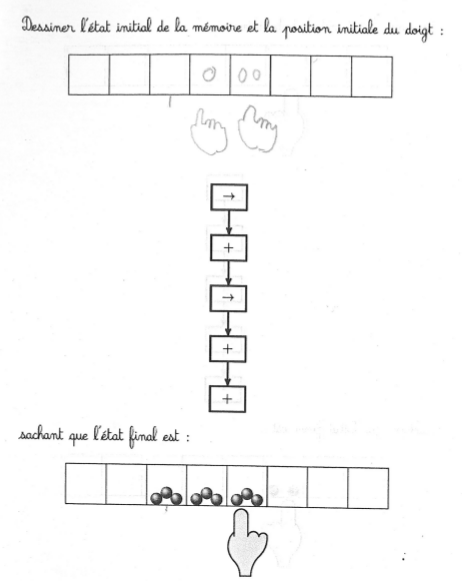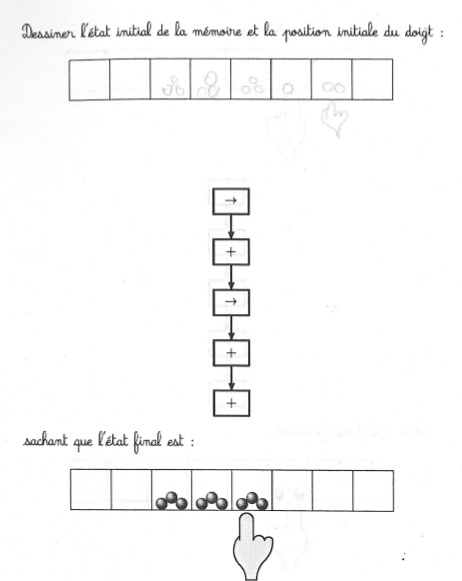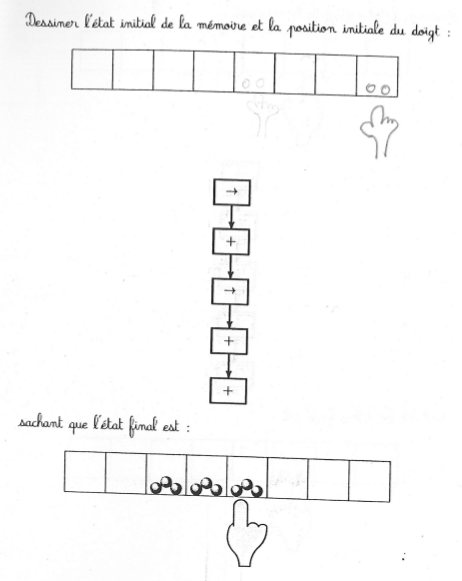
On constate là encore une certaine tendance à appliquer le programme à l’état final, et à dessiner les états intermédiaires sur la fiche.
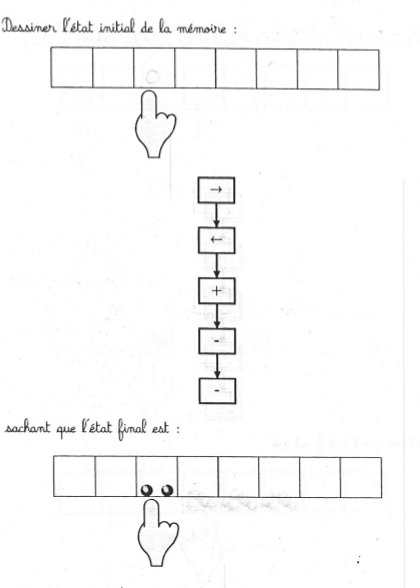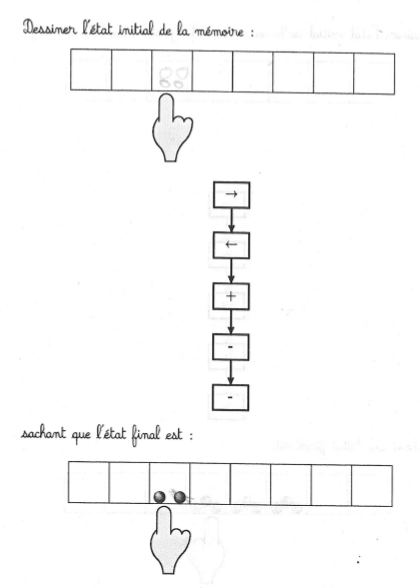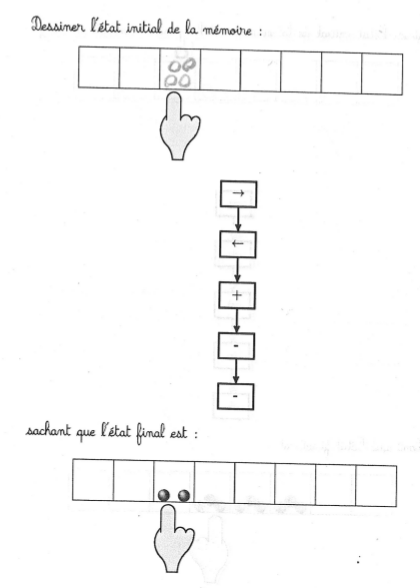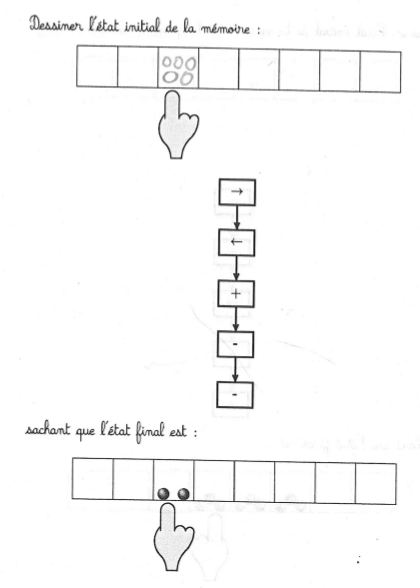
page 13
Le programme se simplifie en une décrémentation, donc on demande quel état initial donne 2 après une décrémentation. Peu d’élèves ont eu le temps de commencer cette page et tous ont trouvé 4 au lieu de 3, sauf celle qui a appliqué la transformation à l’état final :
Bilan
En raison de l’absence d’une enseignante, plusieurs élèves de CP b, qui avaient déjà manipulé la machine (voir plus haut), ont été placés en CE 2. Ils ont insisté pour faire les fiches avec les élèves de CE 2 mais il n’y avait pas assez de fiches pour eux. Ils se sont montrés assez déçus.
Plusieurs élèves de CE 2 se sont montrés réticents à l’idée de confier leurs livrets (pour scanner) car ils n’avaient pas fini les fiches. Il a fallu leur promettre de leur rendre les fiches après le scan.
Il y a même eu des élèves qui ne voulaient pas aller en récréation tant ils préféraient jouer à la machine de Post !



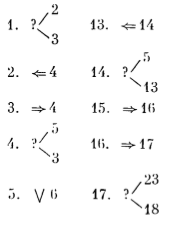


































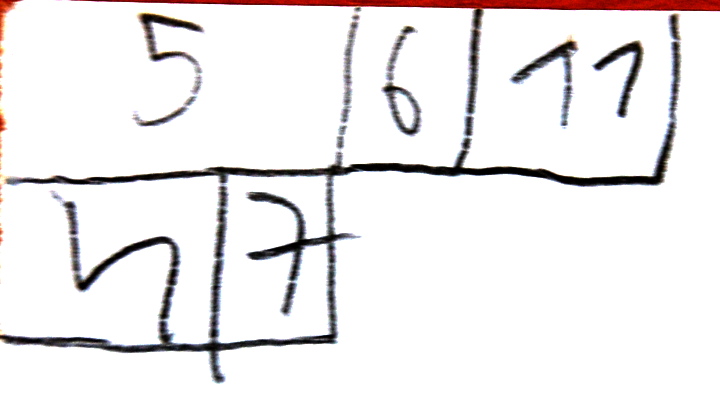













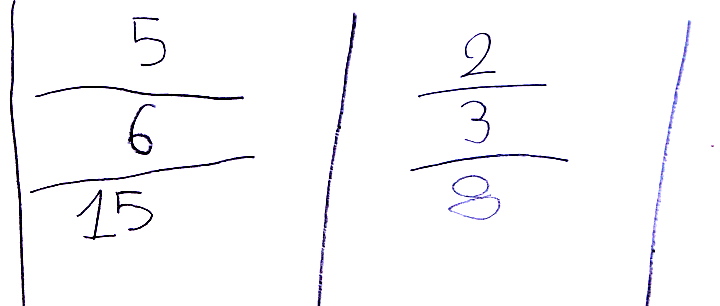































Commentaires