Premier exemple
La suite "à la Fibonacci" $u_{n+1}=u_n+u_{n-1}$ avec $u_0=1$ et $u_1=\frac{1-\sqrt{5}}{2}$ est géométrique de raison $\frac{1-\sqrt{5}}{2}$ donc tend vers 0. Théoriquement...
Si on calcule ses 20 premiers termes avec IDLE :

on trouve qu’elle a bien l’air de tendre vers 0, mais si on pousse un peu plus loin :
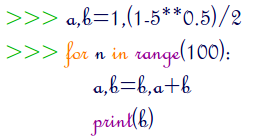
le 100ième terme a l’air plutôt ... divergent :

Le problème en Première est que classiquement, pour prouver que la suite est géométrique, on utilise le raisonnement par récurrence, qui est déjà considéré comme difficile en Terminale...
Mais une fois de plus, on peut (en attendant la Terminale) demander aux élèves de faire confiance en un logiciel de calcul formel, par exemple Maxima et son merveilleux module "solve_rec" :

Une autre difficulté posée par cet exemple est que la récurrence se fait sur deux termes ($u_{n+1}$ fonction de $u_n$ et de $u_{n-1}$). Plus simple en Première serait un exemple où $u_{n+1}$ ne dépend que de $u_n$. Mais un autre exemple de récurrence sur deux termes est cité ici.



Commentaires