Phase d’entraînement

Plus de 80 classes ont participé, dont la plupart issues de jumelages 3^e-2^nde. Le sujet est celui-ci :

L’énoncé du problème 2 n’a pas été rédigé dans le sujet, mais présenté sous forme d’une vidéo que voici :

Quelques productions de classes

Voici une sélection faite par le jury, de quelques productions particulièrement remarquables, avec des explications sur le choix :

Épreuve du 28 mai

Voici le sujet, en pdf :

La question 3 était posée sous forme de vidéo, que voici, allégée pour être lisible en ligne :

QUELQUES PRODUCTIONS

Problème 1

Le problème 1 a donné lieu, pour le jumelage de Terre-Sainte, à une narration de recherche rédigée au format numérique open document presentation, que voici :

Problème 2

Le jumelage Lycée Leverger/Collège Adrien Cerneau a fait un film vidéo pour expliquer la démarche du problème 2. Hélas, faute d’autorisation de publication pour les voix, ce film ne peut être placé ici. Cependant, d’autres groupes ont rendu leur solution sous la forme d’un fichier GeoGebra, tableur voire pdf ; en voici quelques-uns :

Bras-Panon	Chatoire/Lagourgue	EITO/Leconte de Lisle

Clairefontaine (tableur)	Plateau caillou (pdf)

Problème 3

Le problème 3 a donné lieu aux productions les plus variées (et où la persévérance s’est particulièrement remarquée). Notamment des solutions avec GeoGebra :

Bassin bleu/Marie Curie	Jean Albany/La Possession	Terre-Sainte

Le tableur a également été sollicité pour ce problème, soit pour calculer directement par formule, soit pour faire les additions :

Schoelcher/Hoarau	St-Paul 4/Aigrettes	Bellepierre/Dodu	Clairefontaine	Avirons/Lougnon

Plusieurs groupes ont résolu le problème 3 par algorithme. Mais deux d’entre eux ayant choisi AlgoBox qui exporte au format html, leurs productions peuvent être mises en ligne, dont une dans le corps de cet article ; on peut ouvrir chacune dans un nouvel onglet d’un clic droit ci-dessous :

contribution de Bassin-Bleu	contribution de Leconte de Lisle

La première des deux a été choisie parce que, faisant appel à l’interactivité, elle se prête mieux à une mise en ligne. Elle est à tester ici-même :

Une autre contribution numérique mais pas avec AlgoBox :

Là encore, le tableur a été utilisé soit pour faire des simulations, soit pour lister les 216 possibilités et calculer les sommes :

Schoelcher/Hoarau	Terre-Sainte	Clairefontaine

Problème 4

Résoudre le problème à deux dés est facile avec un tableur : On place à la case (i,j) la somme de i et j, et on compte les 9 sur ce tableau bidimensionnel (ou matrice). Mais le problème du Duc est à trois dimensions puisqu’il y a trois dés. Il faudrait donc le résoudre avec un tableur en 3D, qui n’existe pas encore. La figure CaRMetal suivante, extraite de cet article, donne une idée de la complexité de la représentation :

En listant les couples formés par le premier dé et le second, plusieurs groupes ont réussi à faire le décompte en 2D. En particulier, le groupe de Plateau-Caillou, celui de Clarefontaine ci-dessus, et celui de Terre-Sainte, dont voici la contribution :

Problème 5

Le problème 5 a été résolu par le jumelage Chatoire-Trois-mares, sous la forme d’un film, que voici :

Mais en plus, ils ont donné un fichier tableur pour résumer la solution :

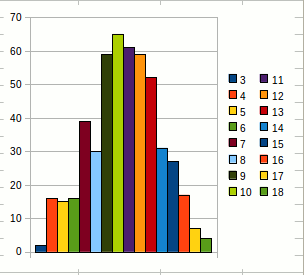
Les productions sélectionnées par le jury sont visibles dans le portfolio ci-dessous ; en général, elles ont été sélectionnées soit parce qu’elles montrent une prise d’initiative, soit parce qu’elles font preuve de persévérance, soit parce que ce sont de bonnes narrations de recherche, soit tout simplement parce qu’elles sont belles... Il est prévu d’afficher certaines d’entre elles à la fête de la science.