Construction du tétraèdre
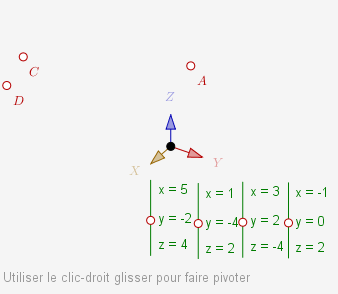
Il faut ouvrir une nouvelle figure 3D (dans le menu « fichiers ») et utiliser la macro « coordonnées 3D » pour créer un point auquel on donne les coordonnées -1, 0 et 2, et que l’on renomme A. Puis on recommence pour avoir B, C et D :
La figure ci-dessus doit être tournée pour voir les sommets B et D (on peut aussi zoomer mais dans ce cas l’angle de vue de la figure devient sensible aux mouvements de la souris).
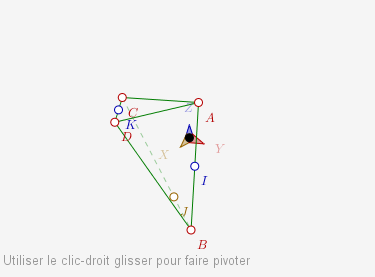
Après quelques coups de gomme sur les coordonnées, l’outil « arêtes 3D » permet de dessiner le tétraèdre :
Comme la perspective cavalière conserve les barycentres, I et K sont construits avec l’outil « milieu ». Et J est construit avec la macro « report de mesure algébrique » (dans « alignement »).
Section du tétraèdre
La question 2.a. ne sera pas traitée ici parce que CaRMetal ne sait pas (encore) calculer les équations de plans [1].
Par contre, la section d’un tétraèdre par un plan passant par des points sur ses arêtes est un exercice classique en Seconde et en Première S.
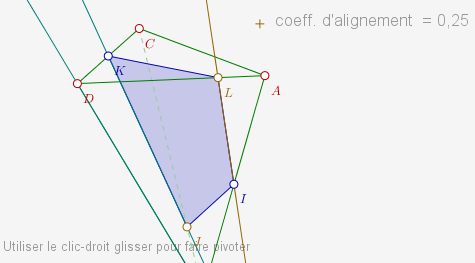
Voici comment un élève de seconde construit la section :
Le point L est apparu par hasard dans la construction, alors on l’a nommé L !
Finalement la macro « coefficient d’alignement » a servi à conjecturer que L est au quart de [AD].


Commentaires