Les mathématiques de lycée au service des jeux vidéos
Depuis quelques années, l’algorithmique et la programmation prennent une place de plus en plus importante dans les programmes de collège et de lycée. Parallèlement à cette arrivée en force de l’algorithmique au lycée, les habitudes de nos élèves ont énormément changé ces dernières décennies. Les jeux vidéos, notamment, ont pour beaucoup d’entre eux une place très importante dans leur vie.
Dans cet article, nous proposerons quelques situations-problèmes extraites de jeux vidéos dont la formulation ne fait pas apparaître les mathématiques, mais dont la résolution entraîne l’utilisation de mathématiques de niveau lycée.
Pour cet article nous utiliserons le logiciel Processing. Voici le site où vous pourrez le télécharger : https://processing.org/. Ce logiciel est initialement proposé avec le langage Java, mais il est depuis peu compatible avec le langage Python.
Comment pourrions nous jouer à un quelconque jeu s’il n’y avait pas de bouton « PLAY » sur lequel cliquer ?
Nous allons créer un bouton avec les caractéristiques suivantes :
- le bouton sera représenté par un cercle de couleur,
- il sera au centre de l’écran,
- il s’affichera en vert si la souris le survole,
- il s’affichera en rouge si l’on clique à l’intérieur du bouton,
- il s’affichera en noir sinon.
Il s’agit ici de savoir à quel moment la souris est à l’intérieur ou à l’extérieur du cercle.
La formule donnant la distance entre deux points connaissant leurs coordonnées sera donc le cœur de notre algorithme.
Il suffira ensuite d’adapter la couleur du cercle en fonction de la position de la souris par rapport au centre du cercle.
centreX = 300
centreY = 300
rayon = 50
distance = 0
# on cree la fonction distance
def dist(xA,yA,xB,yB):
return sqrt(pow(xA-xB,2) + pow(yA-yB,2))
def setup():
# on declare une fenetre de taille 600 x 600
size(600,600)
def draw():
background(51)
# donne la distance entre la souris et le centre du cercle
distance = dist(centreX,centreY,mouseX,mouseY)
if distance < rayon:
if mousePressed:
fill(200,0,0) # on colorie en rouge
else:
fill(0,200,0) # on colorie en vert
else:
fill(0) # on colorie en noir
# on affiche le cercle
ellipse(centreX,centreY,2*rayon,2*rayon)
Le titre parle de lui même : nous voulons créer un effet « lampe torche » à l’écran.
Pour comprendre le principe, il faut préalablement avoir un minimum de notions en représentation des couleurs.
En mode RGB ( Red-Green-Blue), une couleur est codée sur 3 octets donnant chacun la quantité de rouge-vert-bleu qu’il faut pour produire la couleur.
Il est cependant possible de rajouter un quatrième octet pour coder la transparence (on dit « l’alpha ») de la couleur.
Plus l’alpha est proche de 0 ( resp 255) et plus la couleur est transparente (resp opaque)
Voici nos objectifs :
- Afficher une image de fond.
- Recouvrir entièrement cette image de carrés noirs aussi petits que possible
- L’alpha de chaque carré sera calculé en fonction de sa distance à la position de la souris. Il sera de 255 à l’extérieur d’un cercle de centre la souris, et il variera de 0 à 255 pour les points intérieurs selon une fonction à définir, ce qui aura pour effet de créer un dégradé de transparence entre le centre du cercle et le bord du cercle.
- Cet effet de transparence dégradée créera notre effet de lampe torche.
- La notion de distance entre deux points est une fois de plus réinvestie, car nous aurons besoin de calculer si un carré est à l’intérieur ou à l’extérieur du cercle.
- C’est le moment de réinvestir les fonctions de référence pour créer des effets différents de dégradés.
- En seconde on pourra faire intervenir la fonction constante - linéaire - carrée - racine carrée - inverse.
- Les fonctions trigonométriques, logarithmique et exponentielle peuvent venir s’ajouter suivant le niveau des élèves.
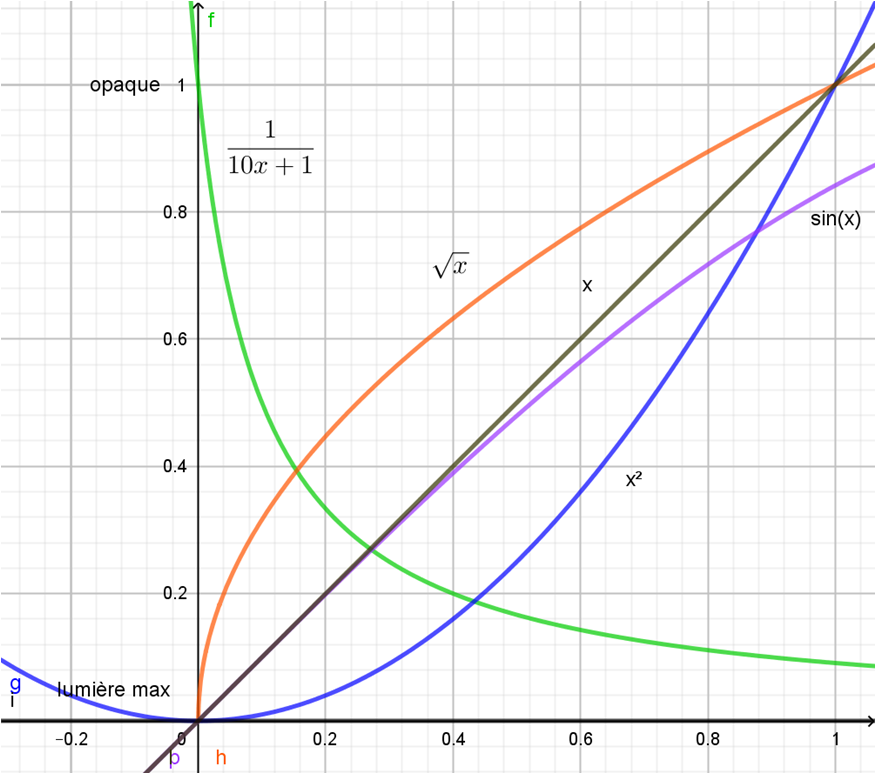
Voici les différentes fonctions utilisées dans notre programme :
- L’axe des abscisses représente la distance à la souris et l’axe des ordonnées représente l’opacité du carré noir.
- Les fonctions sont pensées pour être définie de [0,1] dans [0,1].
- Au moment du code il faudra les « redimensionner » pour qu’elles soient définie de [0, rayon] dans [0, 255].
- Remarquons que pour la fonction sinus (et encore plus pour la fonction inverse) l’image de 1 n’est pas 1, le dégradé de transparence ne sera donc pas parfait au bord du cercle pour ces deux fonctions. Ça peut-être l’occasion de revoir la notion de continuité en un point.
nbTuile = 200
vision = 100 # rayon de la lampe torche
n = 0 # compteur de sélection de la fonction pour la lampe torche
Alpha = 0
# fonction distance
def Distance(xA,yA,xB,yB):
return sqrt(pow(xA-xB,2) + pow(yA-yB,2))
#===================================================================================
#DIFFERENTES FONCTIONS POUR LA LUMINOSITE DE LA LAMPE
# d : distance réelle au centre du cercle
# v : vision cad le rayon du cercle
#===================================================================================
#fct constante
def f0(d , v):
return 0
# fct lineaire
def f1(d , v):
return 255*(d/v)
# fct carré
def f2(d , v):
return 255*pow(d/v,2)
# fct racine carrée
def f3(d , v):
return 255*sqrt(d/v)
# fct sinus
def f4(d , v):
return 255*sin(d/v)
# fct inverse
def f5(d , v):
return 255*(1/(10*d/v+1))
def f(d,v,n):
arrayFunction = [f0(d,v),f1(d,v),f2(d,v),f3(d,v),f4(d,v),f5(d,v)]
return arrayFunction[n]
def setup():
size(400,400)
global largeurTuile,hauteurTuile
largeurTuile = width/nbTuile
hauteurTuile = height/nbTuile
global backGroundImg
backGroundImg = loadImage("chambre.jpg")
noStroke()
# a chaque clic de souris on change de fonction
def mouseClicked():
global n
n=(n+1)%6
def draw():
image(backGroundImg,0,0)
global vision,Alpha
for i in range(nbTuile):
for j in range(nbTuile):
Dist = Distance(mouseX,mouseY,j*largeurTuile,i*hauteurTuile)
if Dist < vision:
Alpha = f(Dist,vision,n)
else:
Alpha = 255
fill(0,Alpha)
rect(j*largeurTuile,i*hauteurTuile,largeurTuile,hauteurTuile)
En anglais le « Tweening » est une abréviation de « in-betweening ».
C’est le nom que l’on donne aux processus permettant de générer des images intermédiaires entre une image de départ et une image d’arrivée pour donner l’illusion d’un mouvement fluide.
Voici les objectifs :
- Nous allons reprendre le code du bouton « PLAY ».
- On ne veut plus qu’il apparaisse directement au milieu de l’écran, mais qu’il se déplace jusqu’à celui-ci.
- Décidons que l’on cache le bouton en haut de l’écran ( dans les Y négatifs).
- On va le faire descendre.
- Le bouton dépassera le milieu de l’écran et continuera sa descente, puis il remontera et s’arrêtera au milieu.
Nous proposons d’utiliser une fonction trigonométrique du type f(t) = a.sin(t)+b pour simuler notre déplacement de bouton :
Posons f(t) = a.sin(t) + b
On a besoin :
- d’un Y de départ ( D )
- d’un Y d’arrivée ( A)
- d’un temps total de parcours ( T )
- du temps déjà écoulé ( t )
Dans ces conditions :
- D= f(0) = b et
- A = f(T) = a sin(T) + D
- ce qui nous donne a = (A-D)/sin(T)
centreX = 300
centreY = 0
rayon = 50
t = 0
timeMax = 2.4
def setup():
size(600, 600)
# fonction de tweening=======================================================
def Sin( depart, arrivee, timeMax, t):
a = (arrivee - depart) / sin(timeMax)
return a * sin(t) + depart
def draw():
background(51)
fill(255)
global t,timeMax,centreY
if t < timeMax:
centreY = Sin(-50,300,timeMax,t)
t+=0.01
ellipse(centreX,centreY,2*rayon,2*rayon)
fill(0)
text("PLAY",centreX-15,centreY)
Des jeux de types « platformer » comme super « Mario Bross » ou « doodle Jump » aux jeux en 3D, la physique a une place cruciale dans la création de jeux vidéos.
Notre objectif ici est d’appliquer la relation fondamentale de la dynamique afin de faire rebondir une balle soumise à la gravitation.
Il faudra que :
- la balle tombe par gravité,
- la balle rebondisse sur les bords de l’écran.
Pour cette partie, les mathématiques sous-jacentes font appel à la notion de vecteur, ainsi que de vitesse et d’accélération ; mais surtout elle fait intervenir la relation fondamentale de la dynamique (RFD).
En mécanique Newtonienne, la RFD s’énonce généralement ainsi :
Dans un référentiel galiléen, considérons un mobile de masse constante m.
Si l’on exerce une force F sur ce mobile alors l’accélération du mobile vérifie l’équation suivante : F = m . a
Puisque la seule force qui s’exerce sur notre balle est son poids, alors P = m.g = m.a, ce qui donne que a = g.
Ensuite connaissant l’accélération instantanée de notre balle, par une méthode de type Euler :
- on obtient sa vitesse instantanée en posant v = v + a *dt
- on obtient sa position instantanée en posant Pos = Pos + v * dt
hauteur = 600
longueur = 800
time = millis()
dt = 0
g = 900
diametre = 50
centre = PVector(longueur/2,0)
V = PVector(-300,0)
A = PVector(0,g)
bounceCoeff = 0.95
def settings():
size(longueur,hauteur)
def Distance( xA, yA, xB, yB):
return sqrt((xA-xB)*(xA-xB) + (yA-yB)*(yA-yB))
def setup():
rectMode(CENTER)
def draw():
background(51)
global dt,time,V,A,centre
dt = millis() - time
time = millis()
#V.x = V.x + A.x*dt/1000;
V.y = V.y + float(A.y*dt/1000) # en pixel/s
centre.x = centre.x + float(V.x*dt/1000) # en pixel
centre.y = centre.y + float(V.y*dt/1000) # en pixel
#rebonds en bas
if centre.y+diametre/2 > hauteur:
centre.y = hauteur-diametre/2
V.y *= -bounceCoeff
V.x *= bounceCoeff
#rebonds à gauche
if centre.x-diametre/2<0:
centre.x=diametre/2
V.x *= -bounceCoeff
V.y *= bounceCoeff
#rebonds à droite
if centre.x+diametre/2>longueur:
centre.x=longueur-diametre/2
V.x *= -bounceCoeff
V.y *= bounceCoeff
fill(0,255,255)
ellipse(centre.x,centre.y,diametre,diametre)
Nous savons cliquer dans un bouton circulaire, mais comment cliquer dans un bouton de forme polygonale ?
Remarquons dans un premier temps que puisque tout polygone (convexe ou non) peut s’écrire comme l’union de triangles, il suffit de savoir cliquer dans un triangle.
Voici nos objectifs :
- créer deux triangles (ils formeront un polygone non convexe),
- faire en sorte que chacun des triangles change de couleur quand on le survole.
La notion mathématique cachée derrière nos objectifs est la notion de produit scalaire.
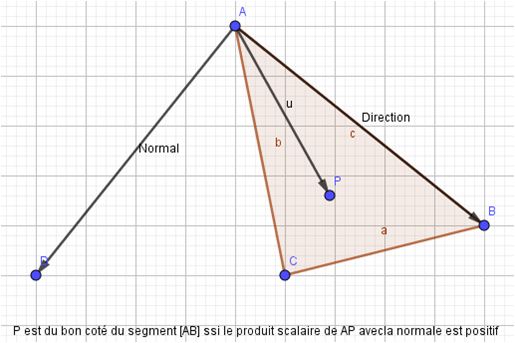
Le signe de du produit scalaire des vecteurs AP et AB nous permettra de savoir « de quel côté » se trouve le point P par rapport au triangle ABC.
En appliquant ce principe aux trois cotés du triangle on saura si le point P appartient ou non au triangle ABC.
Remarquons l’importance de donner les points dans l’ordre, car le produit scalaire avec le vecteur AB sera l’opposé du produit scalaire avec le vecteur BA .
A = PVector(0,50)
B = PVector(300,200)
C = PVector(200,400)
D = PVector(400,150)
def setup():
size(400,400)
def Scalaire(u,v):
return u.x * v.x + u.y * v.y
def IsInTriangle(pA,pB,pC,pos):
Direction = PVector(pB.x-pA.x,pB.y-pA.y)
Normal = PVector(-Direction.y,Direction.x)
posTest = PVector(pos.x-pA.x,pos.y-pA.y)
scl = Scalaire(posTest,Normal)
if scl<0:
return False
Direction = PVector(pC.x-pB.x,pC.y-pB.y)
Normal = PVector(-Direction.y,Direction.x)
posTest = PVector(pos.x-pB.x,pos.y-pB.y)
scl = Scalaire(posTest,Normal)
if scl<0:
return False
Direction = PVector(pA.x-pC.x,pA.y-pC.y)
Normal = PVector(-Direction.y,Direction.x)
posTest = PVector(pos.x-pC.x,pos.y-pC.y)
scl = Scalaire(posTest,Normal)
if scl<0:
return False
return True
def draw():
background(51)
stroke(0)
if IsInTriangle(A,B,C,PVector(mouseX,mouseY)):
fill(255,255,0)
else:
fill(255,0,0)
triangle(A.x,A.y,B.x,B.y,C.x,C.y)
if IsInTriangle(A,D,B,PVector(mouseX,mouseY)):
fill(255)
else:
fill(0)
triangle(A.x,A.y,B.x,B.y,D.x,D.y)
Documents joints
-

- Fichiers Python







Commentaires