Définition
Tout d’abord, il convient de préciser ce qu’est, exactement, un programme de calcul. Une définition cohérente serait « un programme servant à faire des calculs. Mais évidemment cela amène à deux autres questions :
- Qu’est-ce qu’un programme ? (une suite d’instructions à effectuer)
- Qu’est-ce qu’un calcul ? (la construction d’un nombre à partir d’autres nombres)
Du coup, la distinction entre programme de calcul et fonction, n’est pas très nette. Disons qu’un programme de calcul est l’implémentation d’une fonction par un algorithme ne comprenant ni test, ni boucle. Dans le contexte du flow programming c’est un graphe dont aucun sommet n’a un degré sortant supérieur à 1, et ne comportant pas de cycle.
On verra dans cet article que même rédigés en français, les programmes de calcul ne sont pas toujours faciles à suivre, à cause d’ambigüités dans les énoncés, et pas seulement de l’absence de définition d’un programme de calcul.
Polynésie septembre 2023
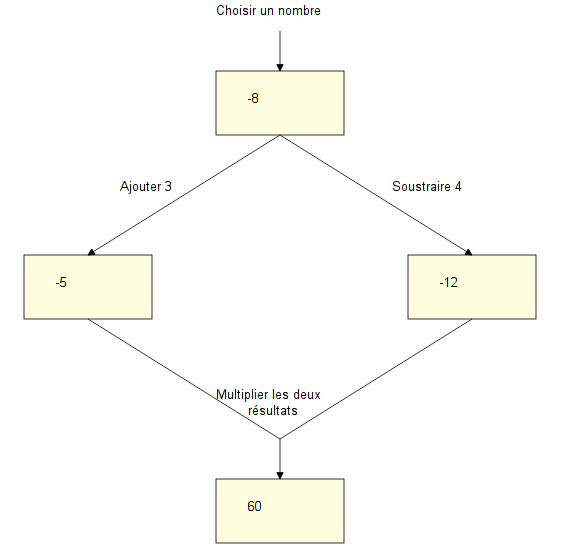
Justement, dans ce sujet, le programme de calcul était donné sous la forme d’un graphe :
On considère le programme A défini par le schéma ci-contre :
a) Vérifier que le résultat est 60 si le nombre choisi au départ est −8.
b) On appelle x le nombre de départ et on admet que le résultat obtenu avec le programme de calcul est donné par l’expression :
(x + 3)(x – 4)
Résoudre (x + 3)(x – 4) = 0.
En déduire quels nombres de départ il faut choisir pour obtenir 0 comme résultat.
(le dessin ci-dessus est cliquable, il permet d’ouvrir une nouvelle page web où on peut modifier le « nombre choisi »)
Et le premier sommet a un degré 2, ce qui le disqualifie selon la définition précédente. En fait, cette bifurcation est liée au fait que le nombre choisi intervient dans 2 calculs intermédiaires.
Centres étrangers 2023
Sujet
Amir et Sonia ont chacun inventé un programme de calcul.
| Programme d’Amir | Programme de Sonia |
| • Choisir un nombre • Soustraire 5 • Prendre le double du résultat |
• Choisir un nombre • Ajouter 3 • Multiplier le résultat par le nombre choisi • Soustraire 16 |
1) Montrer que si le nombre choisi au départ est 6 alors on obtient 2 avec le programme d’Amir et on obtient 38 avec celui de Sonia.
2) Amir et Sonia souhaitent savoir s’il existe des nombres choisis au départ pour lesquels les deux programmes renvoient le même résultat.
Critique
Les candidat.e.s au DNB devaient quand même deviner des choses :
Programme d’Amir
- choisir un nombre (on suppose qu’il est entier ?)
- Soustraire 5 : à qui ? Bon, on n’a choisi qu’un seul nombre donc on comprend que c’est à ce nombre qu’on soustrait 5.
- Prendre le double du résultat : pour en faire quoi ?
Voici une variante :
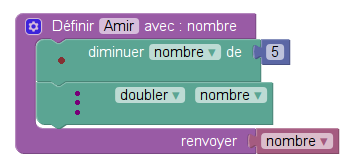
Pour éviter une confusion entre les résultats (même si dans le cas présent il n’y a qu’un résultat), on propose de transformer le nombre en une variable, et plutôt que renvoyer le double d’icelle, la doubler avant de la renvoyer.
Programme de Sonia
- Choisir un nombre : OK
- Ajouter 3 : au nombre choisi, pour l’instant il n’y a pas d’ambigüité
- Multiplier le résultat par le nombre choisi : on suppose que le résultat est celui de l’addition.
- Soustraire 16 : à qui ? au nombre choisi ? au résultat de l’addition ? au résultat de la multiplication ?
On suppose que c’est au résultat de la multiplication puisque c’est la dernière opération effectuée. Mais justement, si on veut que l’expression « le résultat » ne soit pas ambigüe, c’est qu’il s’agit systématiquement du dernier nombre mémorisé. Et dans ce programme de calcul, ce n’est pas toujours le cas, puisqu’à un moment on multiplie par le nombre choisi.
La mémoire de Sonia est donc plus sollicitée que celle d’Amir, puisqu’en plus du « résultat » elle doit aussi avoir gardé en mémoire le nombre choisi. Avec Sofus c’est pareil :
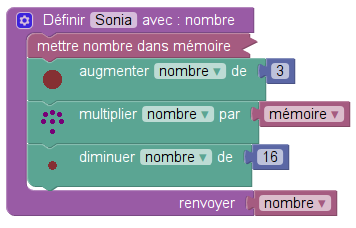
En fait, si on voulait le représenter sous forme d’un graphe, ce programme de calcul ressemblerait à celui de Polynésie (septembre 2023) représenté plus haut, à ceci près que le losange ressemblerait plutôt à un trapèze. On propose cette définition :
Définition : un programme de calcul dont le graphe est une liste chaînée est dit affine.
Le graphe est supposé orienté et les listes sont, dans le langage de la théorie des graphes, appelées des chemins. Ce sont des graphes connexes dont tous les sommets (sauf le départ et l’arrivée) ont un degré entrant et un degré sortant égaux à 1.
Une liste correspond d’ailleurs mieux à l’idée intuitive de programme, avec une puce devant chaque item de la liste.
Les programmes affines sont précisément ceux qui ne demandent pas de mémoriser un résultat antérieur. Je propose de les appeler ainsi parce, justement, la fonction qu’ils permettent de calculer est affine.
La nécessité de mémoriser le nombre choisi, en plus du « résultat », est ici justifiée parce que l’exercice porte sur une fonction qui n’est pas affine : la fin de l’exercice consiste à résoudre une équation produit.
Question 1
1) Montrer que si le nombre choisi au départ est 6 alors on obtient 2 avec le programme d’Amir et on obtient 38 avec celui de Sonia.
Avec Sofus, une fois le programme de calcul défini, on peut récupérer un bloc appelé Amir et comprenant une prise appelée avec : nombre où on place le nombre choisi par Amir. Ensuite on branche le tout sur un bloc « ajouter en bas » qui fera qu’à chaque clic, le résultat sera ajouté en bas de la fenêtre d’affichage de Sofus.
De nombreuses illustrations de cette phase sont présentes plus bas dans l’article, on a fait le choix de ne pas en faire ici. Par contre, Sofus n’oblige pas que le « nombre » choisi soit vraiment un nombre. Il suffit de dire qu’Amir a choisi la lettre x :
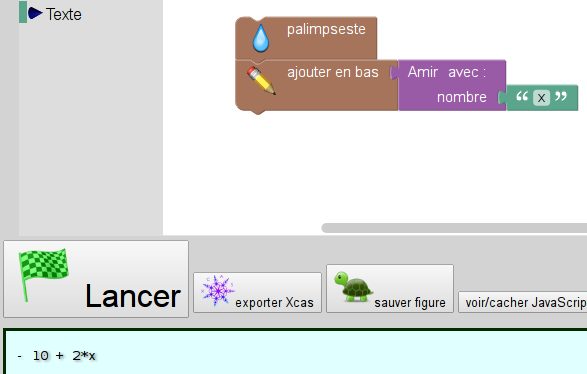
pour avoir la confirmation que son programme est bien affine. Et en faisant la même chose avec Sonia :
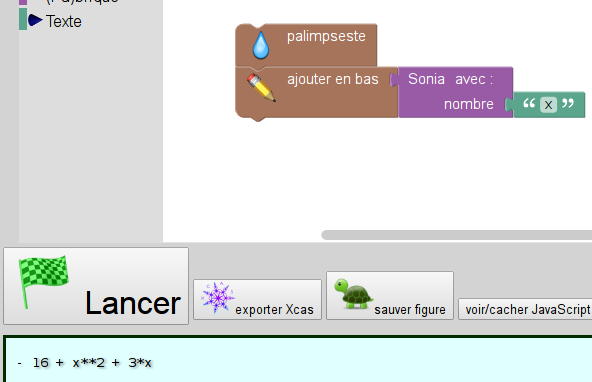
on confirme que son programme à elle n’est pas affine.
Question 2
2) Amir et Sonia souhaitent savoir s’il existe des nombres choisis au départ pour lesquels les deux programmes renvoient le même résultat.
Pour cela ils utilisent un tableur, mais uniquement pour afficher une table de valeurs de la fonction d’Amir, et, juxtaposée à elle, une table de valeurs de la fonction de Sonia. Il est probable que dans la cellule B3 ait été placée une formule du genre
=(B1+3)*B1-16
qui utilise l’algèbre. Alors qu’une feuille de tableur réservée à Sonia permettrait de découvrir (et même représenter graphiquement) la fonction de Sonia, en mettant des nombres dans la ligne 1, et ensuite les formules suivantes dans la colonne A :
-
=A1+3dans A2 -
=A2*A1dans A3 -
=A3-16dans A4
puis en tirant vers la droite ces trois formules, on voit non seulement que pour le nombre 2 en entrée, Sonia trouve effectivement 38, mais aussi pourquoi.
Et pour peu qu’on utilise un tableur ayant du calcul formel comme celui d’Xcas, on peut même prouver que le résultat est x²+3x-16 si l’entrée est x (question 3.a)...
Mais ici, le but était de chercher une solution à l’équation x²+3x-16=2x-10 et pour cela, il fallait voir juxtaposés les deux tableaux de valeurs.
Question 3
a. Montrer que le résultat obtenu par Sonia est donné par x²+3x-16.

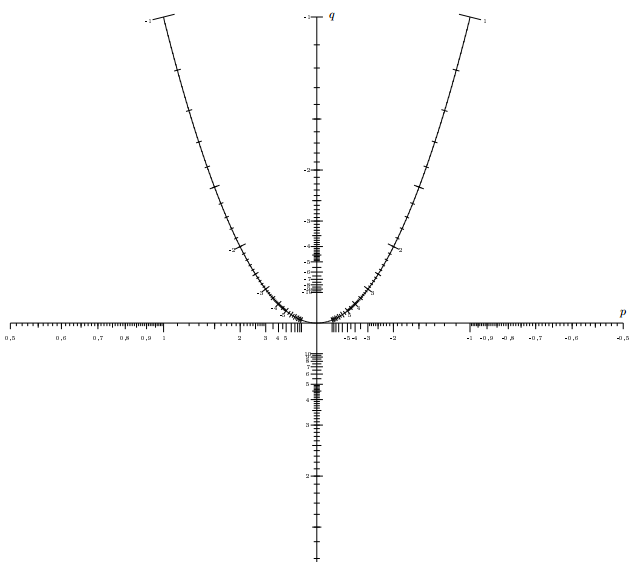
La suite de l’exercice aurait pu être (hors DNB) de transformer l’équation x²+3x-16=2x-10 en x²+3x-16-2x+10=0 puis, après réduction, en x²+x-6=0, et ensuite utiliser ce nomogramme pour résoudre l’équation :
On pose la règle de telle manière qu’elle passe par la graduation 1 (à gauche) sur l’axe des abscisses, et la graduation -6 sur l’axe des ordonnées. La droite coupe la parabole en deux graduations : 2 à droite que l’on connaissait déjà par la question 2, et -3 à gauche qui est donc l’autre solution de l’équation.
Ou alors, on pouvait y aller au calcul formel : on sait d’après ce qui précède que x²+x-6=(x-2)(x-r) où r est l’autre solution de l’équation. Ensuite on développe (x-2)(x-r) pour trouver x²-(2+r)x+2r à comparer avec x²+x-6 : on en déduit que 2+r=-1 et 2r=-6. Résoudre une de ces équations permet de trouver r=-3. Mais ceci dépasse largement le programme de cycle 4. D’ailleurs l’énoncé précisait
b. on admet que les programmes donnent le même résultat si on choisit comme nombre de départ les solutions de l’équation (x-2)(x+3)=0.
La question ne portait finalement que sur la résolution d’une équation produit. Mais dans ce cas, la pertinence de la question 2 est douteuse.
Pour tester avec Sofus, on peut télécharger, dézipper puis ouvrir dans https://alainbusser.github.io/Sofus... le fichier suivant :
Métropole-Antilles-Guyane 2023
Sujet
Ici, on compare aussi deux programmes de calcul mais ils sont affines :
Voici deux programmes de calcul.
| Programme A | Programme B |
| • Choisir un nombre • Multiplier ce nombre par −2 • Ajouter 5 à ce résultat. |
• Choisir un nombre • Soustraire 5 à ce nombre • Multiplier le résultat par 3 • Ajouter 11 au résultat |
Critique
Programme A
• Choisir un nombre
• Multiplier ce nombre par −2
• Ajouter 5 à ce résultat.
Voilà un programme de calcul sans ambigüité ! En Sofus ça donne :
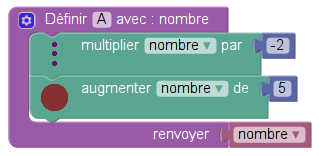
mais il est conceptuellement plus complexe que la version de l’énoncé : dans l’énoncé on ne fait que des calculs alors que le nombre est devenu une variable dans la version Sofus.
Programme B
• Choisir un nombre
• Soustraire 5 à ce nombre
• Multiplier le résultat par 3
• Ajouter 11 au résultat
Une seule ambigüité, à la fin : c’est bien entendu au résultat de la ligne précédente qu’il faut ajouter 11, et non au résultat précédent (celui de la soustraction). Mais pour lever cette ambigüité, il a bien fallu qu’à un moment on considère « le résultat » comme une variable, puisque ses valeurs successives évoluent dans le temps.
C’est donc le choix qui a été fait dans Sofus, en utilisant directement nombre comme variable et en faisant l’économie de la variable résultat :
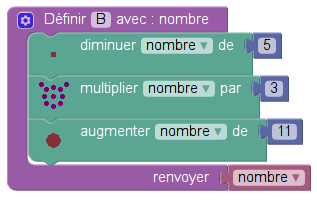
L’utilisation d’une variable (et de Sofus) permet de simplifier encore l’énoncé du programme B :

Question 1
1. a. Montrer que, si on choisit −3 comme nombre de départ, le résultat obtenu avec le programme A est 11.
b. Quel résultat obtient-on avec le programme B si on choisit 5,5 comme nombre de départ ?
Commençons par le a : Maintenant que les programmes de calcul A et B sont entrés dans Sofus, il y a dans la partie (fa)brique qui avait servi à les programmer, deux nouveaux blocs A et B où on peut brancher le nombre choisi. En prenant un bloc A, puis en branchant à sa droite le nombre -3, il suffit de mettre le tout en entrée d’un « ajouter en bas » (de la fenêtre d’affichage).
Mais auparavant, comme la fenêtre d’affichage se remplit vite avec toutes les expériences qu’on mènera par la suite, on commence par effacer celle-ci, selon la tradition médiévale du palimpseste :

En cliquant sur le drapeau vert, on voit apparaître dans la fenêtre d’affichage (en dessous de la fenêtre de travail) le nombre 11.
Question b maintenant. Comme ci-dessus mais cette fois-ci on choisit le programme B au lieu de A et on y branche le nombre 5.5 (pas de virgule mais un point décimal) :

Question 2
2. En désignant par x le nombre de départ, on obtient −2x + 5 comme résultat avec le programme A.
Montrer, qu’avec le même nombre de départ, le résultat du programme B est égal à 3x − 4.
Pour vérifier l’affirmation de l’énoncé, il suffit de mettre la lettre x à la place du nombre choisi :
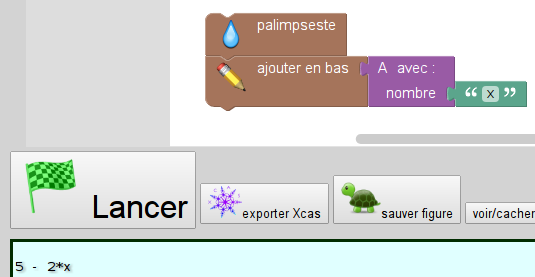
Et pour la question, même chose mais avec le programme B :
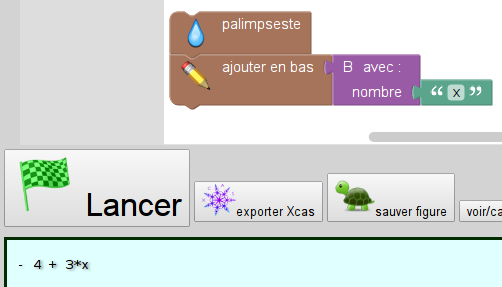
Pour obtenir une preuve avec Sofus, on peut insérer d’autres « ajouter en bas ».
Question 4
4. Déterminer par le calcul le nombre de départ pour lequel les programmes A et B donnent le même résultat.
On a vu à la question 2 que le programme A calcule la fonction affine -2x+5 et le programme B calcule la fonction affine 3x-4 (et ces fonctions affines ont été représentées graphiquement dans la question 3, non traitée ici). Il s’agit donc de résoudre l’équation -2x+5=3x+4. Sofus peut le faire, puisqu’on a obtenu les expressions littérales pour A et B en mettant une lettre (x ; d’où l’adjectif « littéral » pour désigner ce calcul) à la place du nombre, et de ce fait on a obtenu comme résultat, non un nombre, mais du texte. Puisque Sofus arrive à faire des calculs sur du texte, il peut également construire l’équation (qui est également du texte) simplement en écrivant le signe d’égalité entre les deux expressions :
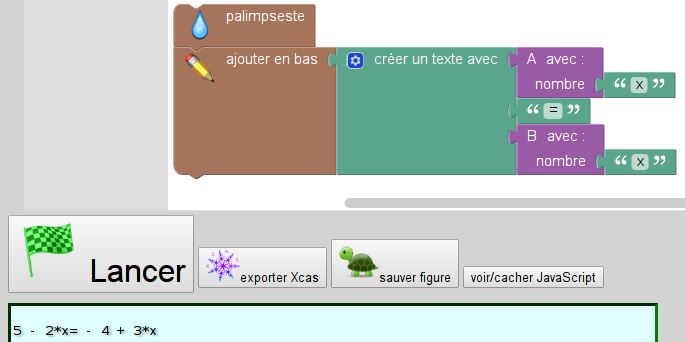
Sofus sait faire d’autres choses que simplement afficher l’équation (qui est, rappelons-le, du texte). Il peut aussi donner ses solutions :
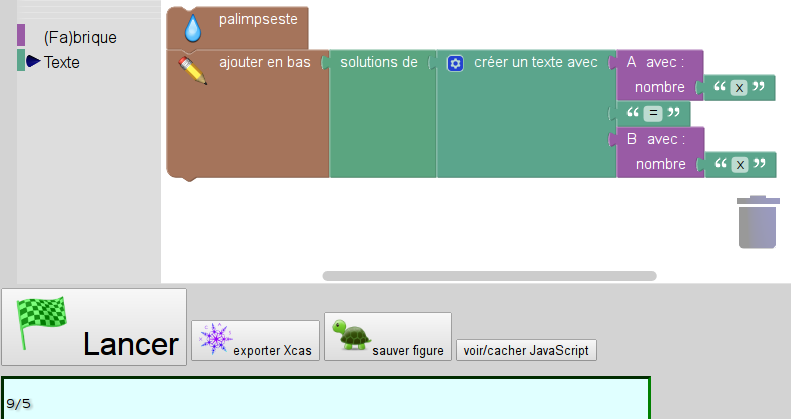
Pour tester avec Sofus, on peut télécharger, dézipper puis ouvrir dans https://alainbusser.github.io/Sofus... le fichier suivant :
Asie 2023
Sujet
Ici, un programme affine déguisé en programme du second degré (les modifications de la variable interviennent après son élévation au carré) :
On considère le programme de calcul suivant :
| Nombre de départ |
| ↓ |
|
| ↓ |
| Résultat |
On revoit le graphe comme dans le sujet de Polynésie septembre 2023 plus haut, mais cette fois-ci le graphe est bien plus simple et ne sont dessinées que deux flèches, rappelant où sont le départ et l’arrivée.
Critique
Bien qu’il ne nécessite pas de mémoire supplémentaire, ce programme n’est pas affine. La raison est qu’au début, on commence par élever au carré la variable. Mais en-dehors de cela, on ne réutilise jamais le nombre de départ et il s’agit en fait d’un programme affine déguisé : il est affine (et même linéaire) s’il s’applique au carré du nombre de départ, et non au nombre lui-même.
• Calculer le carré de ce nombre : et après j’en fais quoi de ce carré [1] ?
• Multiplier par 5 : qui ? le nombre ? son carré ?
• Ajouter 4 : à qui ?
• Multiplier par 2 : on doit faire l’hypothèse que chaque fois c’est sur le résultat de la ligne d’au-dessus qu’on opère...
• Enlever 8 : pourquoi pas « soustraire » ?
Traduit en Sofus, ce programme de calcul devient ceci :
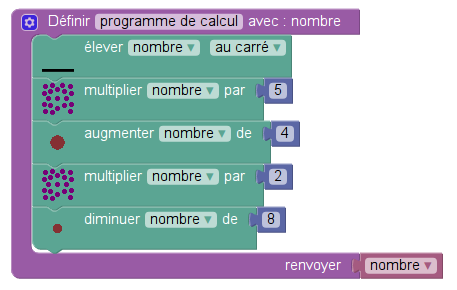
Mais les deux instructions « multiplier par » peuvent être simplifiées, il y a des mots dans la langue française pour ces multiplications :
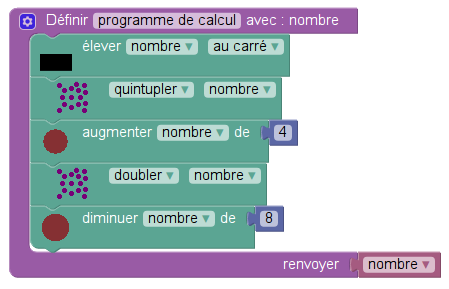
Question 1
1. Montrer que si 3 est le nombre de départ, le programme donne un résultat égal à 90.
Maintenant que le programme de calcul a été défini, il suffit d’y ajouter 3 comme nombre et afficher le résultat :
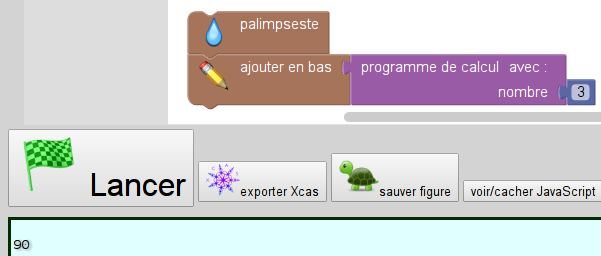
Question 2
2. Un élève choisit 2 comme nombre de départ et un autre élève choisit −2.
Montrer qu’ils doivent obtenir le même résultat.
On peut refaire la même manip qu’à l’onglet précédent en remplaçant 3 par 2 puis par -2 et en vérifiant que dans les deux cas, on obtient 40.
Mais on peut aussi utiliser la réponse de la question suivante.
Question 3
3. Si on nomme x le nombre de départ, montrer que le résultat du programme peut s’écrire 10x².
Il suffit d’entrer comme « nombre choisi » la lettre x :
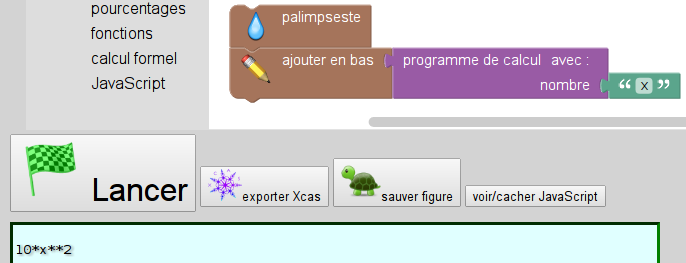
Et on peut faire mieux, en demandant à Sofus d’embellir l’affichage :

Pour tester avec Sofus, on peut télécharger, dézipper puis ouvrir dans https://alainbusser.github.io/Sofus... le fichier suivant :
Polynésie septembre 2023
Sujet
Sujet très intéressant, il n’y a pas de fonctions puisqu’on manipule uniquement des variables globales en Scratch :
On considère le programme de calcul suivant :
• Choisir un nombre
• Prendre le carré de ce nombre
• Multiplier le résultat par 2
• Ajouter le nombre de départ
• Soustraire 66
Critique
• Choisir un nombre : entier ?
• Prendre le carré de ce nombre : et en faire quoi ? Dois-je le rendre un jour, ce carré ? Quand ? À Qui ?
• Multiplier le résultat par 2 : quel résultat ? La prise ?
• Ajouter le nombre de départ : à qui ? (on remarque qu’ici aussi il est nécessaire de mémoriser le nombre de départ puisqu’on doit ensuite l’ajouter à quelque chose)
• Soustraire 66 : à qui ?
Il est précisé plus loin que
On précise que deux variables ont été créées : « nombre choisi » qui correspond au nombre choisi au départ, et « Résultat ».
Les réponses aux questions ci-dessus pourraient bien être « à la variable résultat » sauf pour la première ligne, juste parce que si cette variable « nombre choisi » existe c’est qu’il faut bien s’en servir quelque part...
On obtient alors quelque chose comme ceci :
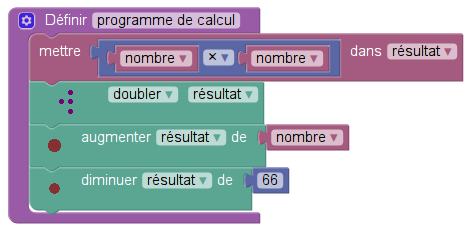
(on remarque que, conformément à la suite de l’énoncé, le programme n’est pas une fonction, mais une procédure : elle ne renvoie rien à la fin, elle ne fait que modifier la variable « résultat »)
Puisqu’on est obligé d’utiliser la variable « nombre » (pour l’ajouter à un « résultat ») vers la fin, on peut aussi l’utiliser dès le début :

Question 1
1) a) Montrer que si le nombre choisi au départ est 4, le résultat obtenu est -30.
b) Quel résultat obtient-on si le nombre choisi au départ est -3 ?
Comme ici il n’y a pas de fonction, on se contente d’exécuter le programme de calcul, et ensuite on affiche la variable résultat :

Pour la question b, on choisit -3 à la place de 4 dans la variable nombre :
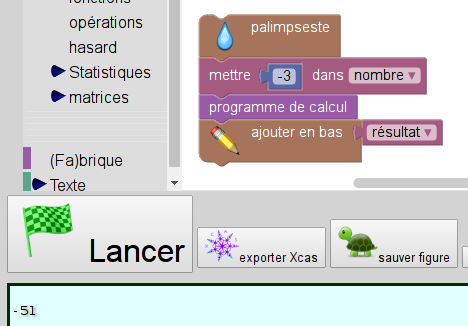
Question 2
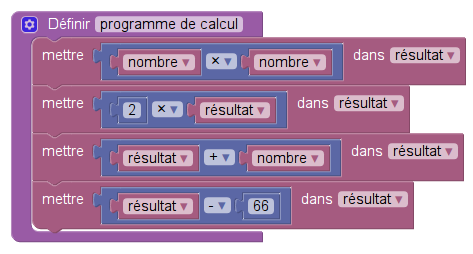
2) a) On s’intéresse au bloc d’instruction ci-dessous intitulé « Programme de calcul ».
On souhaite le compléter pour calculer le résultat obtenu avec le programme de calcul en fonction du nombre choisi au départ.
On précise que deux variables ont été créées : « nombre choisi » qui correspond au nombre choisi au départ, et « Résultat ».
b. Lucie insère le bloc précédent dans le script ci-dessous et observe la réponse donnée par le lutin :

Dans Sofus ce n’est pas le lutin qui dit des choses, mais des affichages ajoutés en bas des anciens affichages. Cette technique fonctionne mieux si on trouve plusieurs solutions.
Le script est améliorable, en ajoutant 0,5 à nombre plutôt qu’en mettant nombre+0.5 dans nombre [2] :
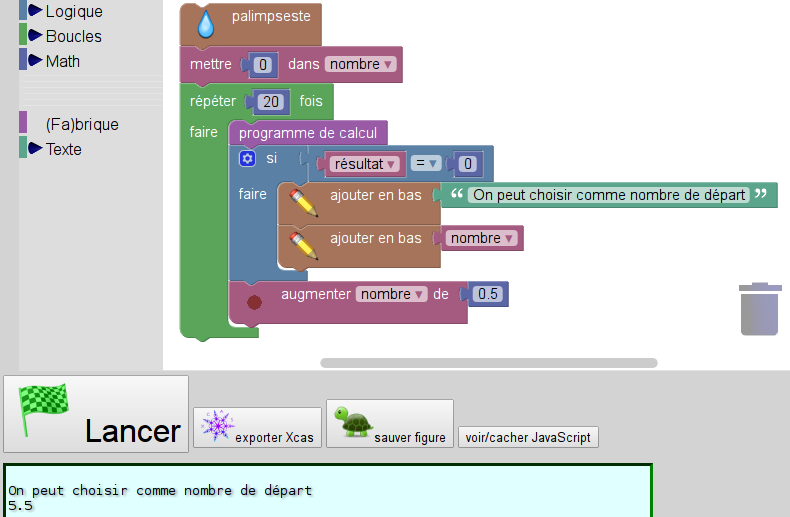
On aurait même pu demander à Sofus (ou à Scratch qui est capable de gérer ce genre de boucles) de faire automatiquement l’augmentation de 0,5 :

Question
3. On nomme x le nombre choisi au départ.
a. Déterminer l’expression obtenue par ce programme de calcul en fonction de x.
b. On admet que (2x − 11)(x + 6) est la forme factorisée de l’expression trouvée à la question précédente.
Pour quelle(s) valeur(s) de x, le résultat obtenu avec le programme est-il égal à 0 ?
Pour la question a, il suffit d’initialiser de choisir un nombre qui n’est pas un nombre [3] mais la lettre x :
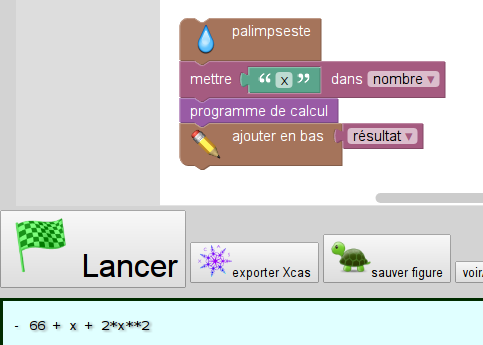
Le résultat admis dans le b peut se vérifier sans avoir à utiliser de parenthèses :

Pour tester avec Sofus, on peut télécharger, dézipper puis ouvrir dans https://alainbusser.github.io/Sofus... le fichier suivant :
Pour conclure, on propose cette définition sofusienne d’un programme de calcul :
Définition : Un programme de calcul est une suite de transformations qu’on applique en séquence à une variable numérique.
La rédaction de cet article a mené à la création d’une nouvelle version de Sofus, consacrée au cycle 4 : elle ne contient que la tortue et les programmes de calcul.


Commentaires