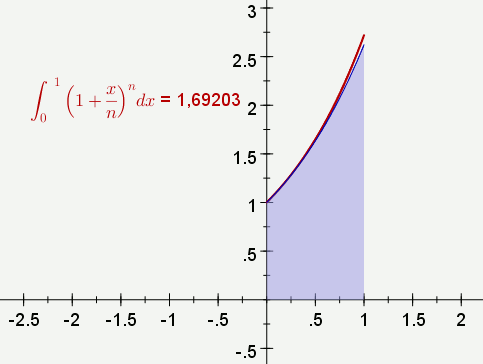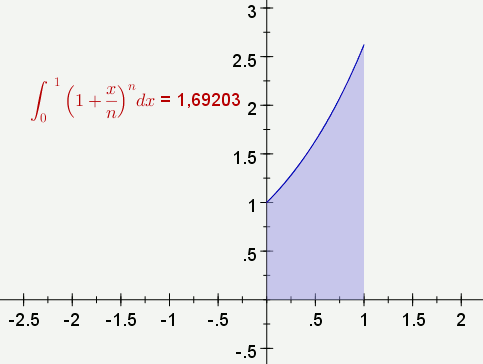
En fait on étudie une suite de fonctions, et n est donc un curseur d’incrément 1. Alors l’expression de la fonction fn (en bleu) est
(1+x/n)^nles bornes étant 0 et 1. La propriété « remplie » a été cochée pour que l’intégrale soit visible sur le graphique :
L’énoncé de la question 2 suggère que la représentation graphique de l’exponentielle soit ajoutée au graphique, ce qui ci-dessus est optionnel grâce à une case à cocher. Pour avoir la valeur de l’intégrale, on a créé une expression [1] dont la valeur est
integrate(f1;0;1)Deuxième partie
Pour calculer une primitive sous wxmaxima, il suffit de cliquer sur l’entrée « intégrer » du menu « calcul ». Ensuite on entre la fonction fn et wxmaxima demande si n=-1 ou non. Après avoir répondu, on a directement la primitive :

Variante : Cocher la case « intégrale définie » et entrer 0 et 1 (en fait c’est déjà fait). Dans ce cas comme on le voit ci-dessus, wxmaxima demande le signe de n, et après avoir répondu, on a la valeur exacte de l’intégrale.


Commentaires