Problème 1 : Sudoku
Introduction
L’annexe du sujet comprend des exemples de découpage en tranches, et le début rappelle qu’une matrice est une liste de listes. La grille de Sudoku est donc une liste de lignes :
M = [[2]+[0]*3+[9,0,3]+[0]*2, [0,1,9,0,8]+[0]*2+[7,4],
[0]*2+[8,4]+[0]*2+[6,2,0], [5,9,0,6,2,1]+[0]*3,
[0,2,7]+[0]*3+[1,6,0], [0]*3+[5,7,4,0,9,3],
[0,8,5]+[0]*2+[9,7]+[0]*2, [9,3]+[0]*2+[5,0,8,4,0],
[0]*2+[2,0,6]+[0]*3+[1]]Chaque ligne est une liste de nombres. La matrice 9×9 ci-dessus ressemble à ceci :
| 200 019 008 |
090 080 400 |
300 074 620 |
| 590 027 000 |
621 000 574 |
000 160 093 |
| 085 930 002 |
009 050 060 |
700 840 001 |
Préliminaire
1. Si la grille est complète, la somme des éléments d’une ligne est 1+2+3+4+5+6+7+8+9 puisque cette somme ne change pas si on trie les termes dans l’ordre croissant. Réciproquement, si la somme est inférieure à 45, c’est qu’il y a au moins un 0 quelque part dans la ligne : La grille est alors incomplète. On va utiliser ce résultat pour simplifier le code de la question suivante.
2. Pour tester si la ligne i est complète, il suffit de comparer la somme de ses termes avec 45 :
def ligne_complete(L,i):
return sum(L[i]) == 45
Pour tester avec un ordinateur les fonctions suivantes, il est nécessaire de programmer aussi les fonctions évoquées dans le sujet sans obligation de les écrire. Les voici donc :
def colonne_complete(L,i):
return sum(L[j][i] for j in range(9)) == 45
def carre_complet(L,i):
return sum(L[j+3*(i//3)][k+(3*i)%9] for j in range(3) for k in range(3)) == 453. La fonction préliminaire qui teste si une grille est complète peut alors s’écrire ainsi :
def complet(L):
ok = True
for i in range(8):
ok &= ligne_complete(L,i)
ok &= colonne_complete(L,i)
ok &= carre_complet(L,i)
return okAnnexes
4. Le code de la fonction ligne de l’énoncé, une fois complété, ressemble à ceci :
def ligne(L,i):
chiffre = []
for j in range(9):
if L[i][j]>0:
chiffre.append(L[i][j])
return chiffreMais avec une liste en compréhension, on pouvait faire plus court :
def ligne(L,i):
return [L[i][j] for j in range(9) if L[i][j]>0]La fonction colonne va d’ailleurs être définie de façon similaire, puisqu’elle n’était pas demandée sous une forme précise :
def colonne(L,i):
return [L[j][i] for j in range(9) if L[j][i]>0]5. Pour l’abscisse, il suffit de calculer les valeurs successives du quotient euclidien de i par 3 : 0,0,0,1,1,1,2,2,2, puis les produits par 3 : 0,0,0,3,3,3,6,6,6. Idem pour les ordonnées.
6. La fonction attendue dans l’énoncé est celle-ci :
def carre(L,i,j):
icoin, jcoin = 3*(i//3), 3*(j//3)
chiffre = []
for i in range(icoin,icoin+3):
for j in range(jcoin,jcoin+3):
if (L[i][j] > 0):
chiffre.append(L[i][j])
return chiffreMais la lettre i désigne, dans ce code, deux variables différentes : Celle qui est passée en argument à la fonction carre, et l’indice de boucle qui est une variable locale : Il n’y a donc pas de risque de conflit entre ces deux variables, mais nommer autrement les indices de boucles (k et l par exemple) aboutit à un code plus clair :
def carre(L,i,j):
icoin, jcoin = 3*(i//3), 3*(j//3)
return [L[k][l] for k in range(icoin,icoin+3) for l in range(jcoin,jcoin+3) if L[k][l]>0]7. La fonction conflit attendue dans l’énoncé peut ressembler à ceci :
def conflit(L,i,j):
return ligne(L,i)+colonne(L,j)+carre(L,i,j)Mais avec les ensembles, on évite les redondances et on se simplifie la suite (la question suivante demande le complément d’un ensemble dans un autre) :
def conflit(L,i,j):
return set(ligne(L,i)+colonne(L,j)+carre(L,i,j))-set([L[i][j]])8. La fonction complétée ressemble maintenant à ceci :
def chiffres_ok(L,i,j):
ok = []
conflit = conflit(L,i,j)
for k in range(1,10):
if (k not in conflit):
ok.append(k)
return okCependant, il est étrange d’avoir nommé « ok » une variable qui n’est pas booléenne, et le mot « conflit » désigne deux choses différentes : une liste (variable locale) et une fonction. En plus, la version avec ensembles est nettement plus concise :
def chiffres_ok(L,i,j):
return set(range(1,10)) - conflit(L,i,j)Naïf
9. Les chiffres que l’on peut écrire à la case (i,j) peut alors être calculé avec
def nb_possible(L,i,j):
return len(chiffres_ok(L,i,j))10. La fonction « corrigée » est celle-ci (les erreurs volontairement introduites concernaient l’indexation à partir de 0 et le double-égal pour les tests) :
def un_tour(L):
changement = False
for i in range(9):
for j in range(9):
if (L[i][j] == 0):
if (nb_possible(L,i,j) == 1):
L[i][j] = chiffres_ok(L,i,j)[0]
changement = True
return changement11. La fonction qui résout par algorithme « naïf » le Sudoku est celle-ci :
def complete(L):
pas_fini = True
while pas_fini:
pas_fini = un_tour(L)
return complet(L)Backtracking
12. La fonction « case suivante » balaye, ligne par ligne, le sudoku :
def case_suivante(pos):
if (pos[1]<8):
return [pos[0],pos[1]+1]
else:
return [pos[0]+1,0]13. La résolution du sudoku par bracktracking se fait par
def backtracking(L,pos):
if pos == [9,0] :
return True
i,j = tuple(pos)
if L[i][j] != 0 :
return backtracking(L,case_suivante(pos))
for k in chiffres_ok(L,i,j):
L[i][j] = k
if backtracking(L,case_suivante(pos)):
return True
L[i][j] = 0
return False
def solution_sudoku(L):
return backtracking(L,[0,0])14. Si p cases sont remplies, il reste 81-p cases. Chacune d’elles est testée au maximum 9 fois, donc l’arbre des appels récursifs de la fonction backtracking ne comprend pas plus de 981-n nœuds.
15. Si le sudoku admet plusieurs solutions, la fonction solution_sudoku renvoie True puisqu’il y a au moins 1 solution. Il en est de même avec la grille initialisée à 0.
16. Une suite de de Bruijn d’ordre 4 sur 3 symboles permettrait de parcourir l’arbre en appelant moins souvent la variable pos.
à propos de Backtracking
Prolog
Le langage de programmation Prolog ne sait faire qu’une chose : Le backtracking. Autant dire que pour résoudre un sudoku, ce langage est particulièrement adapté. C’est l’occasion d’explorer un peu Prolog en ligne et pas seulement sur des sudokus.
sudoku
Pour résoudre le sudoku de l’énoncé, on peut utiliser ce script :
:- use_rendering(sudoku).
:- use_module(library(clpfd)).
sudoku(Rows) :-
length(Rows, 9), maplist(length_(9), Rows),
append(Rows, Vs), Vs ins 1..9,
maplist(all_distinct, Rows),
transpose(Rows, Columns), maplist(all_distinct, Columns),
Rows = [A,B,C,D,E,F,G,H,I],
blocks(A, B, C), blocks(D, E, F), blocks(G, H, I).
length_(L, Ls) :- length(Ls, L).
blocks([], [], []).
blocks([A,B,C|Bs1], [D,E,F|Bs2], [G,H,I|Bs3]) :-
all_distinct([A,B,C,D,E,F,G,H,I]),
blocks(Bs1, Bs2, Bs3).
problem(1,[[2,_,_,_,9,_,3,_,_],
[_,1,9,_,8,_,_,7,4],
[_,_,8,4,_,_,6,2,_],
[5,9,_,6,2,1,_,_,_],
[_,2,7,_,_,_,1,6,_],
[_,_,_,5,7,4,_,9,3],
[_,8,5,_,_,9,7,_,_],
[9,3,_,_,5,_,8,4,_],
[_,_,2,_,6,_,_,_,1]]).
La question
?- problem(1, Rows), sudoku(Rows).
(ne pas oublier le point) fournit alors la solution
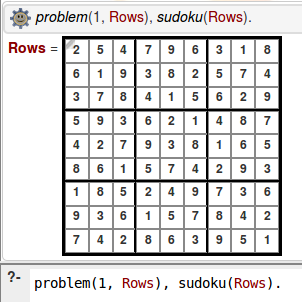
Rows = [[2, 5, 4, 7, 9, 6, 3, 1, 8], [6, 1, 9, 3, 8, 2, 5, 7, 4], [3, 7, 8, 4, 1, 5, 6, 2, 9], [5, 9, 3, 6, 2, 1, 4, 8, 7], [4, 2, 7, 9, 3, 8, 1, 6, 5], [8, 6, 1, 5, 7, 4, 2, 9, 3], [1, 8, 5, 2, 4, 9, 7, 3, 6], [9, 3, 6, 1, 5, 7, 8, 4, 2], [7, 4, 2, 8, 6, 3, 9, 5, 1]]
Que swi-prolog sait afficher plus joliment :
clpfd
La résolution du sudoku avec swi-prolog fait appel à clpfd : Cet acronyme signifie Constraint Logic Programming over Finite Domains, ce qu’on peut traduire par les faits suivants :
- Le domaine que l’on considère est fini (pour le facteur de Mafate par exemple, il y a un nombre fini d’ilets et un nombre fini d’échelles).
- On considère une relation sur ce domaine fini.
- Cette relation est soumise à des contraintes (pour la grille de sudoku, il n’est par exemple pas possible d’avoir deux nombres différents sur une même ligne).
- Le problème peut se résoudre par backtracking (« Logic programming » s’abrège en Prolog) ;
- Le domaine fini peut être représenté par des entiers. C’est par exemple le cas pour le facteur de Mafate.
Voitures
Voici un extrait du sujet de Rallye 2014 :

Cinq voitures disputent une course.
Reconstituez le classement final à l’aide des indices suivants :
- La voiture verte, qui n’a pas gagné, est arrivée avant la voiture bleue, qui ne figure pas sur le podium.
- Deux voitures séparent la voiture jaune de la voiture bleue.
- La voiture rouge a terminé avant la voiture violette, séparées par une voiture.
- La voiture jaune et la voiture rouge ne se suivent pas.
Pour modéliser ce problème en Prolog, on se propose de considérer 5 variables entières Bleue, Jaune, Rouge, Verte et Violette (en Prolog, les noms des variables commencent par des majuscules) puis de traduire les diverses contraintes de l’énoncé. L’égalité est donnée par is et la négation par +. La conjonction est notée par une virgule et la disjonction est notée par un point-virgule :
| Énoncé | Prolog |
|---|---|
| Cinq voitures | permutation([Bleue,Jaune,Rouge,Verte,Violette], [1,2,3,4,5]) |
| La voiture verte, qui n’a pas gagné, | Verte > 1 |
| est arrivée avant la voiture bleue, | Verte < Bleue |
| qui ne figure pas sur le podium | Bleue > 3 |
| Deux voitures séparent la voiture jaune de la voiture bleue | (Jaune is Bleue+3; Bleue is Jaune+3) |
| La voiture rouge a terminé avant la voiture violette, séparées par une voiture | Violette is Rouge+2 |
| La voiture jaune et la voiture rouge | \+ (Jaune is Rouge+1) |
| ne se suivent pas | \+ (Rouge is Jaune+1) |
Le script Prolog au complet est celui-ci :
course([Bleue,Jaune,Rouge,Verte,Violette]) :-
permutation([Bleue,Jaune,Rouge,Verte,Violette], [1,2,3,4,5]),
Verte > 1,
Verte < Bleue,
Bleue > 3,
(Jaune is Bleue+3; Bleue is Jaune+3),
Violette is Rouge+2,
\+ (Jaune is Rouge+1),
\+ (Rouge is Jaune+1).Il fournit cette solution :

Mafate
Voici un niveau du facteur de Mafate :

Il signifie que
- les échelles sont, dans l’ordre croissant, de longueurs 3,4,5,6,7,8 et 9 (on va donc imposer, comme contrainte, que la variable Echelles soit une permutation de ces nombres) ;
- les ilets autres que ceux de départ et d’arrivée) sont, dans l’ordre croissant, de hauteurs 1,2,4,7,8 et 10 (une fois qu’on ajoute les ilets de hauteur 3 et 9, on va donc également avoir comme contrainte, que la variable Ilets soit une permutation de 1,2,3,4,7,8,9,10) ;
- le premier ilet que le facteur doit visiter est de hauteur 3 (en Prolog on écrira ça debut(Ilets,3)) ;
- le dernier ilet que le facteur visitera sera de hauteur 9 en Prolog on écrira ça fin(Ilets,9)).
Reste à programmer les utilitaires debut, fin, et surtout deltas, qui associe à la liste des hauteurs, celle des différences entre hauteurs :
- s’il y a moins de deux ilets, la liste des échelles est vide.
- sinon, c’est que la liste des ilets commence par les ilets de hauteurs A et B, suivis par une liste résiduelle T, et que
- N est la différence entre A et B, dans un certain ordre ;
- N est positif (c’est une distance) ;
- les échelles disposées entre l’ilet B et les suivants constituent une liste D1 ;
- En ajoutant cette liste D1 à N, on obtient la liste d’échelles D.
- Dans ce cas la liste D est celle des échelles joignant les ilets de la liste L :
deltas(L,[]) :-
length(L,N),
N < 2.
deltas([A,B|T],D) :-
( N is B-A; N is A-B),
N > 0,
deltas([B|T],D1),
append([N],D1,D).Pour dire que la liste commence par D, on demande juste que l’élément de la liste de numéro 1 soit égal à D ; par contre pour dire que la liste se termine par Fin, on demande que, si la liste est de longueur N, l’élément numéro N de la liste soit égal à Fin :
fin(Liste,Fin) :-
length(Liste,N),
nth1(N,Liste,Fin).
debut(Liste,D) :-
nth1(1,Liste,D).Avec ces utilitaires, le script résolvant le niveau du facteur de Mafate est celui-ci :
mafate(Ilets,Echelles) :-
debut(Ilets,3),
fin(Ilets,9),
permutation(Ilets,[1,2,3,4,7,8,9,10]),
deltas(Ilets,Echelles),
permutation(Echelles,[3,4,5,6,7,8,9]).En entrant ?- mafate(I,E). on apprend alors que
E = [5, 4, 3, 6, 9, 8, 7],
I = [3, 8, 4, 7, 1, 10, 2, 9](on rappelle qu’en Prolog, la virgule représente une conjonction).
Skyscrapers
Ce sujet est extrait du rallye 2017 (sujet d’entraînement). On constate (même si ce n’était pas évoqué dans le sujet) qu’il s’agit de sudoku 4×4, au sens où les blocs 2×2 contiennent chacun une seule fois chacun des chiffres 1,2,3 et 4. Le premier des utilitaires ad hoc est celui qui donne la liste, dans l’ordre décroissant, des gratte-ciels visibles depuis la droite (ou l’Est). On la définit par récurrence :
- s’il n’y a qu’un seul gratte-ciel, il est le seul à être visible ;
- sinon,
- si le gratte-ciel suivant est plus petit que le dernier gratte-ciel visible, on ne le voit pas et il n’est pas rajouté à la liste ;
- sinon, il est visible et on le rajoute au début de la liste.
En Prolog, cette fonction s’écrit ainsi :
ndecr([A],[A]).
ndecr([N|L],D) :-
ndecr(L,D),
nth0(0,D,M),
N < M.
ndecr([N|L],D) :-
ndecr(L,D1),
nth0(0,D1,M),
N > M,
append([N],D1,D).Pour obtenir la liste des immeubles visibles depuis la gauche,
- on inverse la liste des immeubles de la rangée ;
- on calcule, par la fonction précédente, la liste des immeubles visibles depuis la droite, de la rangée inversée ;
- on inverse le résultat :
ncr(L,D) :-
reverse(L,M),
ndecr(M,D1),
reverse(D1,D).Le nombre nd (dans l’ordre décroissant) des immeubles visibles depuis la droite, est tout simplement la longueur de la liste précédente. Idem pour le nombre des immeubles visibles depuis la gauche. Et les nombres d’immeubles visibles depuis le nord et depuis le sud, s’obtiennent en appliquant ces fonctions à la transposée de la matrice des immeubles :
no(L,N) :-
ncr(L,D),
length(D,N).
nd(L,N) :-
ndecr(L,D),
length(D,N).
ouest([A,B,C,D],[Aw,Bw,Cw,Dw]) :-
no(A,Aw), no(B,Bw), no(C,Cw), no(D,Dw).
est([A,B,C,D],[Ae,Be,Ce,De]) :-
nd(A,Ae), nd(B,Be), nd(C,Ce), nd(D,De).
nord(M,N) :-
transpose(M,P),
ouest(P,N).
sud(M,N) :-
transpose(M,P),
est(P,N).Le fait qu’il n’y a jamais deux immeubles de même hauteur dans une rangée s’exprime en disant que la matrice est stochastique :
stochastique([A,B,C,D]) :-
permutation(A,[1,2,3,4]),
permutation(B,[1,2,3,4]),
permutation(C,[1,2,3,4]),
permutation(D,[1,2,3,4]).Et le fait qu’il en est aussi de même pour les colonnes, s’exprime en disant que la matrice est bistochastique, ce qui veut dire qu’elle est stochastique et que sa transposée est aussi stochastique :
bistochastique(M) :-
stochastique(M),
transpose(M,N),
stochastique(N).Ces utilitaires permettent maintenant de définir une fonction skyscraper ayant pour arguments
- une liste N des nombres d’immeubles visibles depuis le nord ;
- une liste W des nombres d’immeubles visibles depuis l’ouest ;
- une liste E de nombres d’immeubles visibles depuis l’est ;
- une liste S de nombres d’immeubles visibles depuis le sud (ce sont les listes qui bordent la matrice dans le sujet) ;
- et une matrice M (ou NY !) contenant les hauteurs (a priori, inconnues) des immeubles (autrement dit, M est une carte tridimensionnelle de la ville).
Cette fonction est maintenant plutôt courte (on a tout fait pour) :
skyscraper(N,W,E,S,M) :-
bistochastique(M),
nord(M,N),
ouest(M,W),
est(M,E),
sud(M,S).Elle résout les deux questions du sujet :
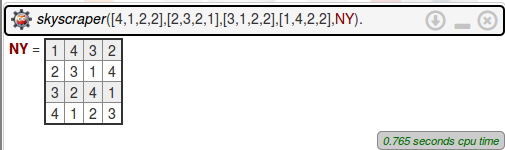
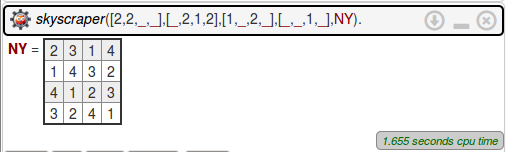
Problème 2 : Enveloppes convexes
Introduction
Dans le sujet, un point est une liste de 2 nombres. Mais pour peu que l’on importe les fonctions du module turtle, on a un objet Vec2D qui peut, en tant que vecteur, être soustrait à un autre « vecteur » (un point en fait) et qui possède une norme notée abs. Pour connaître la distance entre les points (des points Vec2D en l’occurence) P(3,2) et Q(8,5) il suffit donc de faire ainsi :
from turtle import *
P = Vec2D(3,2)
Q = Vec2D(8,5)
print abs(Q-P)Préliminaires
1. L’annexe du sujet ne fait aucune allusion au module turtle (voir onglet précédent) et il n’était donc pas prévu d’utiliser les vec2D de la tortue. Mais il est explicitement fait allusion au module math qui possède une fonction hypot permettant de calculer la longueur de l’hypoténuse d’un triangle, à partir des longueurs (ou mesures algébriques) des côtés de l’angle droit. Le code suivant devait donc, a priori, être autorisé :
from math import *
def distance(P,Q):
return hypot(Q[0]-P[0],Q[1]-P[1])2. Ce script permet d’obtenir la distance minimale en
- établissant la liste des distances non nulles entre deux points du nuage ;
- triant cette liste dans l’ordre croissant ;
- lisant le premier terme de la liste triée : C’est forcément le minimum :
def distance_minimale(L):
ds = [distance(p,q) for p in L for q in L if distance(p,q)>0]
ds.sort()
return ds[0]3. Pour avoir la distance maximale, on peut faire ainsi :
def distance_maximale(L):
ds = [distance(p,q) for p in L for q in L if distance(p,q)>0]
ds.sort()
return ds[len(ds)-1]à gauche toute !
La fonction donnant l’indice du point d’abcisse minimale peut ressembler à ceci :
def point_abs_min(L):
indice= 0
i = 1
minx = L[0][0]
miny = L[0][1]
while i<len(L) :
if L[i][0]<minx:
minx = L[i][0]
indice = i
if L[i][0] == minx:
if L[i][1]<miny:
miny = L[i][1]
indice = i
i += 1
return indiceCet algorithme est en O(n) puisqu’il n’y a qu’une boucle et qu’elle n’est parcourue qu’une fois.
Orientation
5. Si (P,Q,R) est en orientation directe, (Q,R,P) l’est aussi et (P,R,Q) ne l’est pas. On peut justifier cela à l’aide des propriétés du déterminant ou par les permutations : (Q,R,P) est une permutation paire (un cycle) donc ne change pas le signe du déterminant, et (P,R,Q) est une permutation impaire.
6. Avec le module turtle on a une conversion en vecteurs (via une conversion en tuple) qui permet de raccourcir le code :
from turtle import *
def vecteur(A,B):
a = Vec2D(*tuple(A))
b = Vec2D(*tuple(B))
return b-a
def orientation(P,Q,R):
u = vecteur(P,Q)
v = vecteur(P,R)
d = u[0]*v[1]-v[0]*u[1]
if d>=0 :
return 1
else :
return -1Tri
7. Voici l’algorithme de tri à bulle proposé dans le sujet :
def tri_bulle(L):
n = len(L)
for i in range(n):
for j in range(n-1,i,-1):
if L[j]<L[j-1]:
L[j],L[j-1] = L[j-1],L[j]a. Avec la liste L proposée dans le sujet, les états successifs de L sont donnés ici :
[5, 2, 3, 1, 4]
[1, 5, 2, 3, 4]
[1, 2, 5, 3, 4]
[1, 2, 3, 5, 4]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 5]b. La propriété « Après k itérations, les k premiers éléments sont dans l’ordre croissant et inférieurs aux autres éléments » se démontre par récurrence sur k. En appliquant cette propriété à k=n, on démontre que après n itérations, la liste est triée.
c. Dans le meilleur cas, la liste est déjà triée et aucun échange n’est fait. La complexité se mesure alors au nombre de comparaisons, et est proportionnelle au nombre de passages dans la boucle interne. Ce nombre est (n-1)+(n-2)+...+3+2+1=n(n-1)/2 : Complexité en O(n²). Dans le pire cas, la liste est triée dans l’ordre décroissant, et n(n-1)/2 affectations simultanées seront faites : Là encore, la complexité est en O(n²).
8. La fonction fusion est celle-ci :
def fusion(L1,L2):
if len(L1) == 0 :
return L2
elif len(L2) == 0 :
return L1
else:
if L1[0]<=L2[0] :
return [L1[0]]+fusion(L1[1:],L2)
else:
return [L2[0]]+fusion(L1,L2[1:])a. On s’en sert pour la fonction tri_fusion :
def tri_fusion(L):
n = len(L)
if n<=1 :
return L
else:
m = n//2
return fusion(tri_fusion(L[0:m]), tri_fusion(L[m:n]))b. La fonction tri_fusion se termine parce qu’à chaque appel récursif, la longueur des listes à fusionner est divisée par 2.
c. Si n=2p, à chaque appel récursif, les listes à fusionner sont de longueur moitié de la longueur à l’étape précédente, donc de la forme 2k. La complexité de la fusion des listes est alors en O(2k+2k) soit en O(2k+1). Ce qui permet de démontrer par récurrence sur p que, tant dans le meilleur cas que dans le pire cas, la complexité est en O(p×2p).
Jarvis
9. Voici la fonction « naïve » :
def jarvis(L):
n=len(L)
EnvConvexe=[]
for i in range (n) :
for j in range (n) :
Listeorientation=[]
if i!= j :
for k in range (n) :
if k!= i and k!= j :
Listeorientation.append(orientation(L[i],L[j],L[k]))
a=Listeorientation[0]
sommet=True
for v in Listeorientation:
if (v!=a):
sommet=False
if sommet and (i not in EnvConvexe) :
EnvConvexe.append(i)
if sommet and (j not in EnvConvexe):
EnvConvexe.append(j)
return EnvConvexea. La variable sommet est initialisée à True parce qu’on suppose que le point d’indice k est un sommet de l’enveloppe convexe. On parcourt, dans la boucle sur v, les orientations des points du nuage, à la recherche d’un point qui infirmerait cette hypothèse. Si on en trouve un, la variable sommet est positionnée à False puisqu’il suffit d’un contre-exemple pour infirmer l’hypothèse.
b. La double boucle sur i et j donne lieu à n² tests d’égalité entre i et j. La boucle sur k est donc parcourue n²-1 fois et k est affecté n(n²-1)=n³-n fois. Comme i est différent de j, la fonction append est donc appelée n³-n-2 fois. Ensuite on parcourt n²-n fois la liste des orientations, laquelle est de taille n-2. La fonction append est donc encore appelée, au maximum, (n²-n)(n-2)=n³-3n²+2n fois. En tout elle est donc exécutée n³-3n²+n-2 fois, et la complexité de l’algorithme est en O(n³).
c. Le script suivant trace bien un polygone puisque ses arguments sont une liste d’abscisses et une liste d’ordonnées. Mais si ce polygone passe bien par les sommets de l’enveloppe convexe,
- d’une part il n’est pas fermé puisque les coordonnées de son dernier point ne sont pas les mêmes que celle du premier point ;
- d’autre part les points ne sont pas parcourus dans l’ordre qui aurait fait de ses côtés, ceux de l’enveloppe convexe.
Les deux défauts sont apparents sur ce nuage de points gaussiens :
Voici le script en question :
import matplotlib.pyplot as plt
Enveloppe = jarvis(L)
plt.plot([L[i][0] for i in Enveloppe], [L[i][1] for i in Enveloppe])
plt.show()Jarvis 2
10. Sur la figure de l’énoncé, l’ordre des points par rapport au point 6 est : 0,4,1,7,2,5,8,3.
11. La fonction donnant l’indice du prochain sommet de l’enveloppe convexe dans le nuage de points est celle-ci :
def prochain_sommet(L,p):
q = EJ[0]
if q==p:
q=EJ[1]
for k in EJ:
if k!=p and k!=q and orientation(L[p],L[k],L[q])>0:
q = k
return qPour aller plus vite, on a stocké dans la variable EJ la liste des points de l’enveloppe convexe donnée par l’algorithme de Jarvis.
12. La fonction de l’énoncé donnant l’enveloppe convexe à l’aide de la fonction précédente, une fois complétée, ressemble à ceci :
def jarvis2(L):
i = point_abs_min(L)
suivant = prochain_sommet(L,i)
Enveloppe = [i,suivant]
while (suivant != i):
suivant = prochain_sommet(L,suivant)
Enveloppe.append(suivant)
return EnveloppeElle donne ce genre de dessin :
Graham-Andrew
14. La fonction en Python sans le tri initial :
def graham_andrew(L):
EnvSup=[]
EnvInf=[]
for i in range(len(L)):
while len(EnvSup)>=2 and orientation(L[i],L[EnvSup[-1]],L[EnvSup[-2]]) <= 0 :
EnvSup.pop()
EnvSup.append(i)
while len(EnvInf)>=2 and orientation(L[EnvInf[-2]],L[EnvInf[-1]],L[i]) <= 0 :
EnvInf.pop()
EnvInf.append(i)
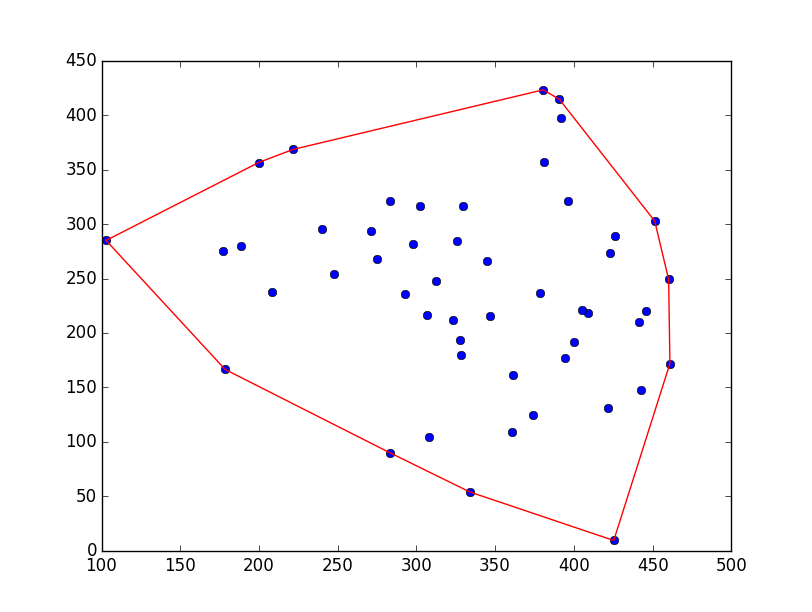
return EnvInf[:-1]+EnvSup[::-1]En effet le tri est fait en place avec
nuage.sort(key=lambda p: p[0])
Voici l’effet de cette fonction sur un nuage gaussien :
a. Comme il y a 8 points, i prend successivement les valeurs 0 à 7.
| i | EnvSup | orientation négative |
| 0 | 0 | - |
| 1 | 0,7 | oui |
| 2 | 0,1 | oui |
| 3 | 0,4 | oui |
| 4 | 0,6 | non |
| 5 | 0,6,5 | oui |
| 6 | 0,6,3 | non |
| 7 | 0,6,3,8 | - |
b. Les instructions append sont effectuées chacune une seule fois dans la boucle, et prennent donc un temps fini ; quant aux instructions pop, elles n’enlèvent que des points qui avaient été placés auparavant et ce n’est jamais un de ces points qui est ajouté après. Il n’y a donc pas de boucle sans fin dans ce programme.
c. La boucle sur i est effectuée n fois. Dans cette boucle il y a un nombre indéterminé de réductions de la liste EnvSup, mais le nombre total de ces réductions ne peut être supérieur à n parce qu’on ne peut pas vider une liste vide. Par conséquent le nombre d’opérations dans la boucle est majoré par 2n (en fait, 2n-2 parce que les réductions ne se font pas sur une liste de taille inférieure à 2). Il en est de même pour la boucle sur EnvInf : Après le tri du nuage de points, la suite est en O(n). Mais comme le tri est lui-même en O(n log(n)), c’est l’opération de tri qui est la plus longue dans cet algorithme, qui est donc aussi en O(n log(n)).




Commentaires