Sujets
On propose ici
- un sujet sur les PPAC, inspiré de celui de l’X 2010
- un sujet sur le transport d’informations dans un arbre, inspiré de celui de l’X 2011
- un sujet sur la représentation des entiers sous forme d’arbres, inspiré de celui de l’ENS 2002
- un sujet sur les arbres de décision, inspiré de celui de Centrale 2013
- l’exercice 3 du sujet 0
Parents
Un arbre est un graphe, une façon naturelle de le modéliser est celle des listes d’adjacence :
- Un dictionnaire qui, à chaque nœud de l’arbre, associe la liste de ses enfants,
- ou une liste de listes (d’adjacence) si les clés du dictionnaire sont des entiers successifs.
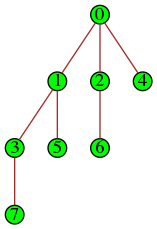
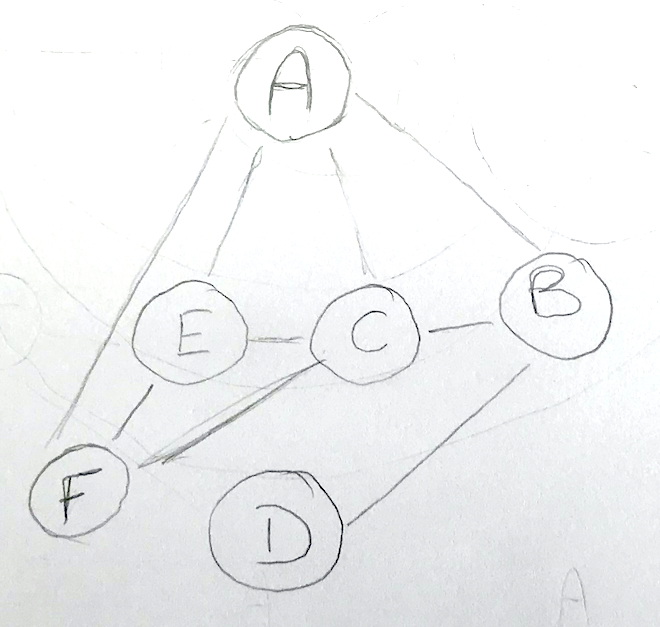
Par exemple l’arbre du sujet X 2010 :
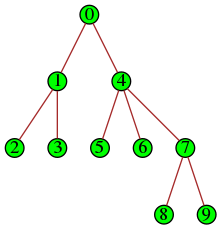
peut être modélisé en Python par un dictionnaire (voir l’onglet suivant) ou cette liste de listes :
[ [1,4],
[2,3],
[],
[],
[5,6,7],
[],
[],
[8,9],
[],
[]]Le sujet Centrale 2000 introduit une nouvelle façon de représenter les arbres :
Ce sujet évoque une fonction père qui, à tout nœud (sauf la racine), associe son unique parent (ou « père »). Il s’agit d’une fonction partielle puisque la racine n’a pas de père. Mais comme l’ensemble des nœuds de l’arbre est fini, cette fonction père est entièrement déterminée par son tableau de valeurs. Par exemple pour l’arbre du sujet X 2010, le tableau des pères est :
| nœud | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| père | aucun | 0 | 1 | 1 | 0 | 4 | 4 | 4 | 7 | 7 |
En Python on le code par
parent = [None,0,1,1,0,4,4,4,7,7]
Cette représentation est plus concise que la représentation traditionnelle par liste d’enfants, parce que, si chaque nœud (sauf les feuilles) peut avoir plusieurs enfants, il n’a qu’un seul parent. Par contre certains algorithmes sont plus faciles à mettre en œuvre sur la représentation traditionnelle.
Avec cette représentation par liste de parents, il est aisé de la racine de l’arbre.
La notion d’ancêtres mène assez naturellement à celle d’ancêtres communs, à laquelle l’onglet suivant est consacré.
PPAC
Les ancêtres communs (AC) de deux nœuds a et b d’un arbre G forment une liste :
def AC(a,b,G):
return [s for s in G if est_ancetre(s,a,G) and est_ancetre(s,b,G)]Parmi tous ces ancêtres communs, le plus petit est par définition celui qui est le plus éloigné de la racine. La notion de plus petit ancêtre commun est assez régulièrement abordée en CPGE, comme un outil servant à résoudre d’autres problèmes, ou en liaison avec la bio-informatique (notion d’arbre phylogénétique). Mais au concours Polytechnique de 2010, c’était le thème majeur du sujet :

Voici le sujet qui a été donné en devoir maison aux élèves de terminale NSI du lycée Roland-Garros :
Et voici le devoir rendu par un des élèves au format html (choix spontané) :
BioPython
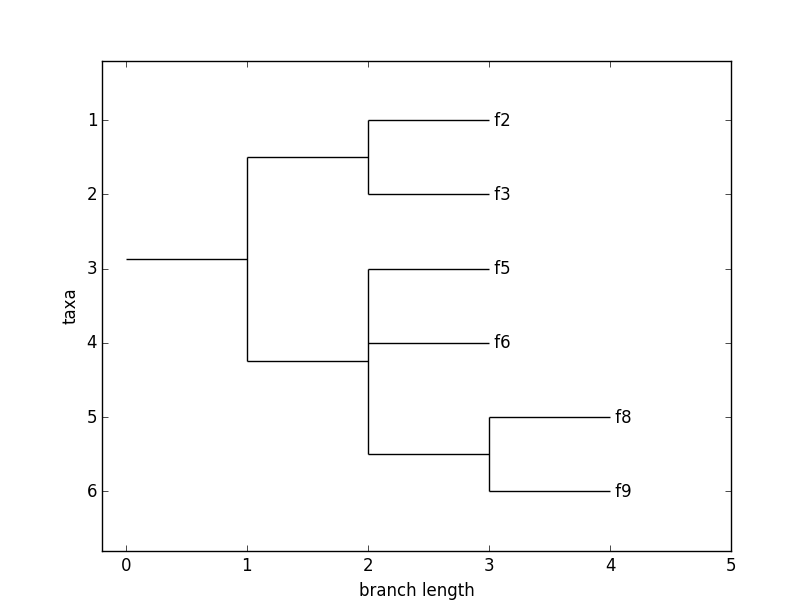
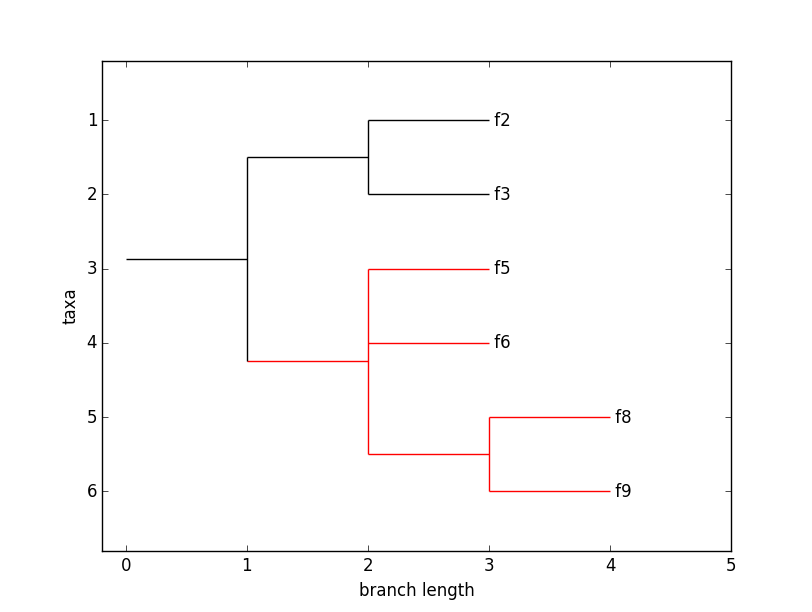
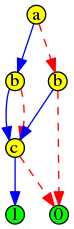
Pour chercher le plus proche ancêtre commun aux taxons numéros 5 et 8, on peut tenter un
ppac = tree.common_ancestor({"name":'f5'}, {"name":'f8'})
print(ppac)Mais dans ce cas on obtient
Cladece qui n’est pas très explicite : cela revient à dire que le plus proche ancêtre commun est un nœud de l’arbre (ne possédant pas de nom), ce dont se doutait un peu. Pour le dessiner, on propose de le colorier en rouge dans l’arbre tree et de dessiner la nouvelle version de cet arbre :
ppac.color='red'
Phylo.draw(tree)ce qui donne l’affichage suivant :
Comme on le voit, BioPython ne fait pas la distinction entre un arbre et un nœud de l’arbre.
Diffusion
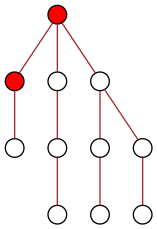
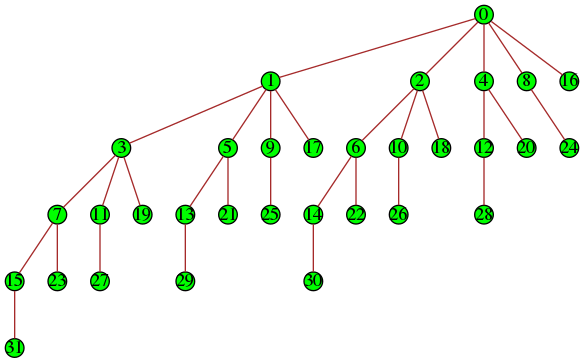
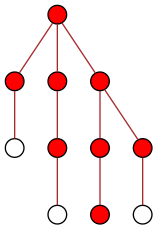
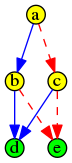
Le sujet X 2011 portait sur la diffusion d’un message dans un arbre, à partir de la racine :
On a un arbre (pas nécessairement binaire) sur lequel on doit diffuser une information à tous les nœuds. Au début seule la racine dispose de l’information :

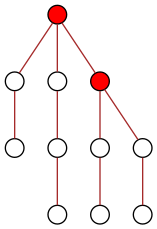
Mais à un instant donné, un nœud ne peut diffuser l’information qu’à un seul de ses enfants. Au bout du temps t=1, seuls deux nœuds disposent alors de l’information, la racine et un de ses enfants :
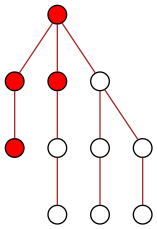
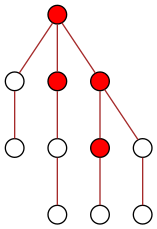
La situation s’améliore ensuite puisque chacun des deux nœuds peut diffuser l’information à un (autre) de ses enfants :
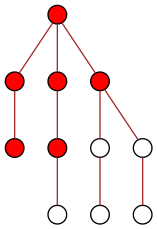
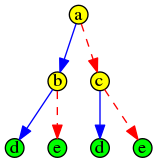
Au temps t=3, la racine diffuse l’information au seul de ses enfants qui n’était pas encore au courant, et lui passe en quelque sorte le relais :
Au temps t=4, seule la partie droite de l’arbre est encore à traiter :
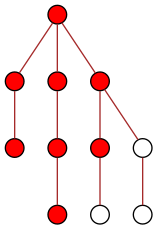
Cela permet au temps t=5 de diffuser l’information à deux nœuds en même temps (venant de leurs pères respectifs) :
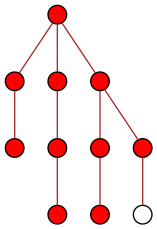
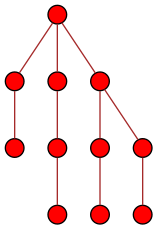
Et au temps t=6, tous les nœuds de l’arbre disposent de l’information :
Entiers
Le sujet ENS 2002 portait sur le théorème de Goodstein :
Ce qui est intéressant avec ce sujet, c’est qu’il propose entre autres une manière de représenter les entiers naturels par des arbres binaires. Et même plusieurs puisque l’arbre obtenu dépend de la base. Ici on va le faire en base 2 seulement. Voici les représentations obtenues :
| Nombre | Arbre binaire |
| 0 | |
| 1 | 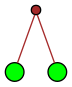
|
| 2 | 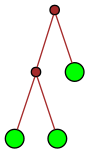
|
| 3 | 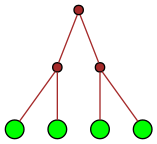
|
| 4 | 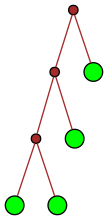
|
| 5 | 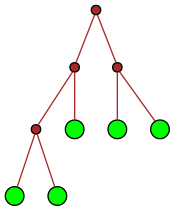
|
| 6 | 
|
| 7 | 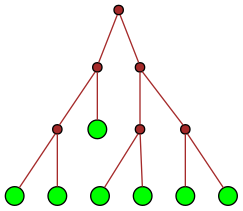
|
| 8 | 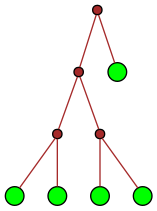
|
| 9 | 
|
| 10 | 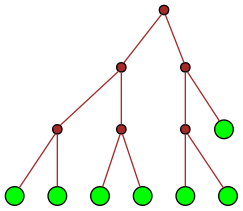
|
| 11 | 
|
| 12 | 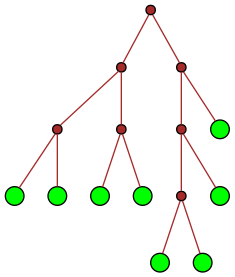
|
| 13 | 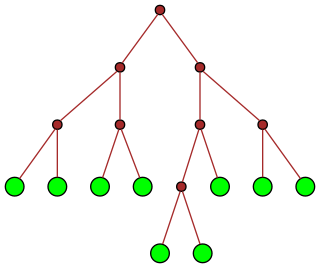
|
| 14 | 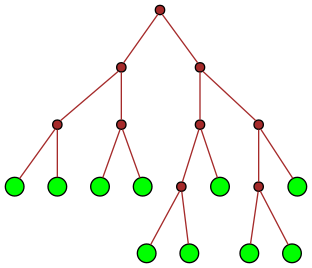
|
| 15 | 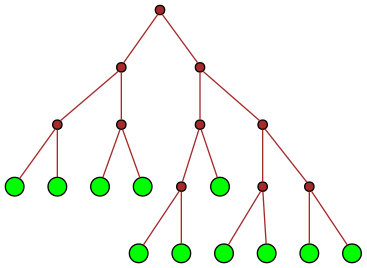
|
| 16 | 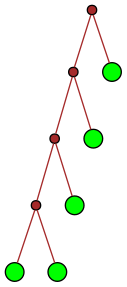
|
| 17 | 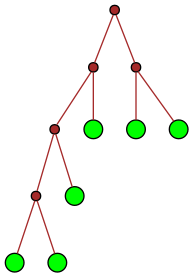
|
| 18 | 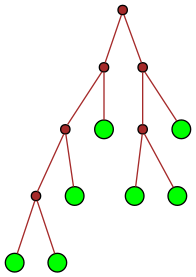
|
| 19 | 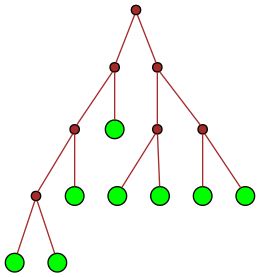
|
| 20 | 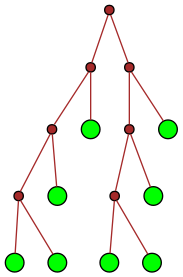
|
| 21 | 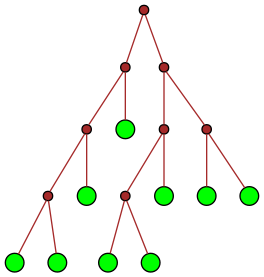
|
| 22 | 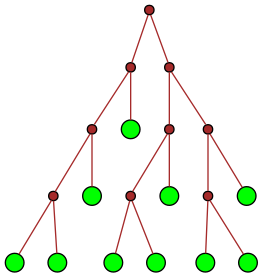
|
| 23 | 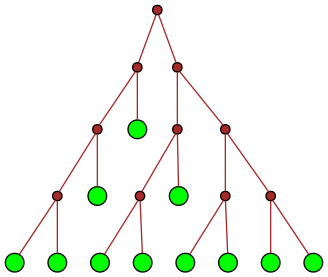
|
| 24 | 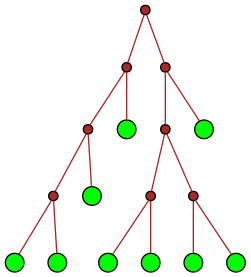
|
| 25 | 
|
| 26 | 
|
| 27 | 
|
| 28 | 
|
| 29 | 
|
| 30 | 
|
| 31 | 
|
| 32 | 
|
Ce sujet est en relation avec le jeu Hydra décrit ici :
Décision
Le sujet Centrale 2013 portait sur la notion d’arbre de décision. Un tel arbre est un arbres binaire. Le fils gauche représente la valeur vrai et le fils droit représente la valeur faux :
L’exemple introductif est intéressant :
- on note e la proposition « le candidat a réussi l’examen »
- on note a la proposition « le candidat a été assidu »
- on note r la proposition « le candidat a réussi au rattrapage ».
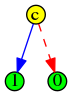
Avec ça, le 1 désigne l’admission à l’examen, et s’obtient ainsi :

La partie basse de l’arbre signifie que seuls les étudiants assidus ont droit au rattrapage, ce qui en dit long sur la situation actuelle des études supérieures...
On verra dans l’onglet suivant que les arbres syntaxiques sont intéressants parce que les opérations sont, en général, binaires (à deux opérandes). C’est le cas de and et or notamment. Ces opérations booléennes étant à deux opérandes, on s’attend assez logiquement à voir des arbres binaires en logique. Mais la surprise est que le seul opérateur booléen ternaire (à trois opérandes), est à l’origine de ces arbres binaires ! En fait si chaque nœud a deux enfants, il a également un parent [6].
L’opérateur ternaire
En fait, en logique booléenne, on n’utilise guère qu’un opérateur ternaire, et on l’appelle l’opérateur ternaire ou, en anglais, if then else, ci-dessous abrégé en IFT.
« If t then e1 else e2 » peut se dessiner par cet arbre (qui est un arbre de décision) :
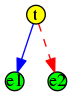
ou par l’expression Python
e1 if t else e2
La puissance de cet opérateur ternaire vient de ce qu’il est possible de s’en servir pour définir les autres opérateurs booléens.
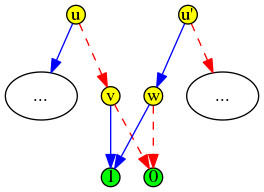
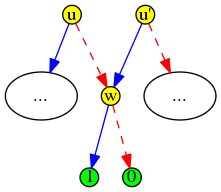
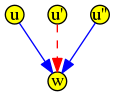
Voici comment on peut représenter sous forme d’arbres de décision, les opérations booléennes élémentaires :
| non x | x ou y | x et y |

|
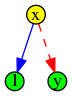
|

|
Il est donc possible de convertir n’importe quelle expression booléenne en arbre de décision (donc, avec les simplifications vues ci-dessus, en graphe de décision).
Syntaxe
Si on invoque Sympy avec
from sympy import *
from sympy.printing.dot import *
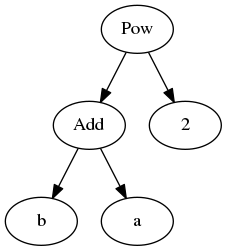
from sympy.abc import *alors on peut représenter sous forme d’arbres (syntaxiques) les expressions (a+b)² et a²+2ab+b² :
dotprint((a+b)**2)
donne cet arbre
et
dotprint(expand((a+b)**2))
donne celui-là :
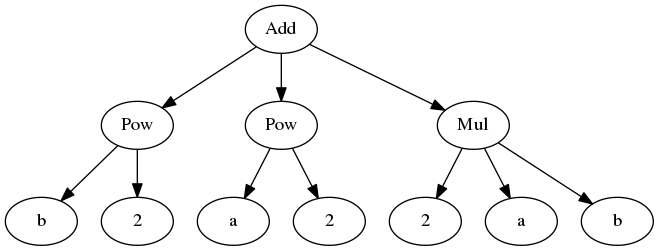
On voit que le premier arbre est celui d’un produit, et le second, celui d’une somme.
Pour aller plus loin, voir
- ces arbres syntaxiques dessinés avec Scratch et CaRMetal,
- cet exerciciel de niveau collège sur les arbres syntaxiques]
- Le dessin de phrases sous formes d’arbres, par Spacy, vu à la fin de cet article.
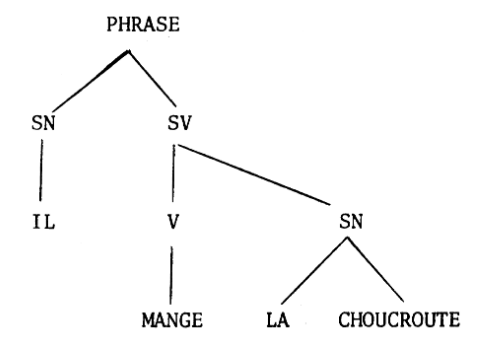
Cet arbre a été dessiné par Alain Colmerauer lors de la conception du langage Prolog, basé sur la représentation de phrases en français, par des arbres :
Arbres binaires
Voici un sujet « type bac imaginé faute de sujet zéro » donné en terminale, dont la première moité portait sur les arbres binaires :
Et voici un sujet sur les arbres binaires de recherche :
En fait, l’arbre de Stern-Brocot peut être vu comme un arbre binaire de recherche de fractions.
D’autres arbres sont visibles dans cet article (onglet plantes). La tortue de Sofus aussi aime les arbres :

Sujet 0
La numérotation de Jérôme de Sosa permet de stocker tout un arbre binaire dans un tableau. Dans un tel cas, la recherche d’un élément dans un arbre binaire de recherche ainsi codé, revient à une recherche dichotomique dans le tableau (trié). Mais l’énoncé de l’exercice 3 omettant l’adjectif « dichotomique », toute recherche devrait être valorisable, y compris celle-ci, inspirée par le devoir d’un élève :
def recherche(arbre,element):
return element in arbreVoici le sujet :
Pour la démonstration de la question 2, la première partie (prouver que h≤n) est considérée comme évidente : la hauteur maximum pour un arbre binaire est atteinte pour un arbre unaire et vaut alors le nombre de nœuds.
Pour la seconde partie (prouver que n≤2h-1) ça a été plus divers :
- preuve par récurrence
- utilisation de la formule pour la somme des termes d’une suite géométrique
- utilisation de la question 2.3 :
Ajouter une unité à la hauteur à l’arbre revient au maximum à doubler son nombre de sommets, ce qui correspond à un maximum de 2h sommets. Mais comme la racine est seule sur sa hauteur, on peut enlever 1 nœud au résultat.
Pour la question 3, beaucoup d’élèves trouvent la fonction
def indice_du_père(i):
if i%2==0:
return i//2
else:
return (i+1)//2Mais peu d’entre eux pensent à utiliser directement i//2.
Voici des solutions proposées par les élèves pour la dernière question :
Comme arbre[0] n’est pas utilisé dans la numérotation de Sosa (on peut y mettre None par exemple), certains élèves ont choisi d’y stocker la longueur du tableau :
def rechercher(arbre,element):
nb_noeuds = arbre[0]
n = 1
while n <= nb_noeuds:
if arbre[n]==element:
return True
if arbre[n]<element:
n = 2*n+1
else:
n = 2*n
return FalseComme l’arbre est stocké dans un tableau, il suffit de chercher si l’élément est dans le tableau :
def recherche(arbre,element):
if element in arbre:
return True
else:
return FalseRemarque : aucun élève n’a opté pour la solution récursive :
def rechercher(arbre,element,i):
if i>len(arbre):
return False
else:
if element==arbre[i]:
return True
else:
if element<arbre[i]:
return rechercher(arbre,element,2*i)
else:
return rechercher(arbre,element,2*i+1)Clément Lagier, de terminale NSI au lycée Roland-Garros, propose ce corrigé du sujet zéro (hormis l’exercice 2) :
Les arbres pondérés sont évoqués à la fin de cet article.






















Commentaires