Piles
Voici un devoir sur les piles et leur utilisation en Forth (langage) :
En voici une version améliorée, par Nathalie Brasset du lycée d’Ottawa :
Et une autre (sous licence CC-by-NC), par Romain Janvier du lycée les trois sources :
En quoi ces versions sont-elles améliorées ? On remarque que la fonction dup par exemple, s’applique à une pile donnée en argument, ce qui permet de programmer en Forth avec plusieurs piles.
Pour aller plus loin, on peut également programmer en PostScript [1] et même y faire un peu de Sofus :
Et ce jeu de Donald Knuth permet de se familiariser avec la notion de pile. Il s’agit d’utiliser une pile pour trier des nombres.
Tri par files
Une variante du jeu précédent est inspirée par le sujet donné au concours ENS en 2011, lequel montre comment on peut trier des entiers avec plusieurs [2] files :
Un invariant de l’algorithme est « toutes les files sont triées ».
En attribuant à chaque nombre de la permutation de départ, la couleur de la file qu’il a traversée au cours du tri, on obtient une coloration d’un graphe :


Mais quel est ce mystérieux graphe ?
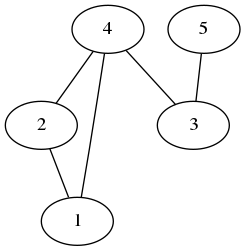
Le cas 3 files est le plus fréquent, et il est rare d’avoir besoin de plus de 4 files.
Plouf-Plouf...
Le problème original est connu sous le nom de problème de Josèphe. Il s’agit d’un problème de permutation lié à des formulettes d’élimination. C’est d’ailleurs cette version plus pacifique que nous allons illustrer ici, comme l’indique le titre de la section.

L’origine historique du problème de Josèphe n’est pas complètement déterminée. On l’attribue à Flavius Josèphe, historiographe judéen du Ier siècle, ayant beaucoup écrit sur les conflits de son temps entre Rome et Jérusalem, mais le travail de Laurent Signac [3] conclut que c’est probablement les Problèmes plaisants et délectables de C.G. Bachet [4] qui ont fait connaître le problème de Josèphe.
En disposant de cartes, on peut même en faire un tour de magie.
Une liste circulaire
Comme le problème parle d’une ronde, la première idée qui semble naturelle c’est d’essayer de modéliser cette ronde.
Une file indienne
Dans cette variante, on imagine la ronde déroulée et transformée en une file d’attente. Ici par exemple Astérix qui est en tête de file, se voit relégué en fin de file par le centurion :

Une fois qu’Astérix est en fin de file, le centurion élimine du jeu, le guerrier goth (en pantalon jaune) qui va donc sortir définitivement du jeu :

En effet le centurion élimine un joueur sur deux et relègue les autres joueurs à la fin de la file. En regardant la file ci-dessus de gauche à droite, on voit que
- le second goth (en fourrure) est à son tour relégué en fin de file,
- le grec est éliminé,
- l’égyptien est relégué en fin de file,
- le breton (en flanelle bleue) est éliminé,
- le belge (en chemise à carreaux) est relégué en fin de file.
Ainsi, lorsqu’Astérix est à nouveau en tête de file, celle-ci est composée d’Astérix, suivi par le goth en fourrure, suivi par l’égyptien, suivi par le belge. Astérix est éliminé (puisque juste avant lui, le belge était relégué en fin de file), et

- le goth en fourrure est relégué en fin de file,
- l’égyptien est éliminé,

- le belge est relégué en fin de file, laquelle est maintenant constituée du goth en fourrure et du belge.

Mais comme le belge vient à nouveau d’être relégué en fin de file, le goth en fourrure est éliminé, et le belge se retrouve à nouveau en tête de file : il est le gagnant du jeu puisqu’il reste le seul dans la file.

Ce jeu est une métaphore d’un système d’exploitation, les guerriers dans la file symbolisant des processus en attente. Lorsqu’un processus quitte momentanément la file, il est dans l’état en cours, et :
- s’il retourne dans la file c’est que le système d’exploitation l’a remis dans l’état en attente ;
- s’il est éliminé c’est que le système d’exploitation l’a mis dans l’état terminé.
Type abstrait de données
Imaginons le meneur debout devant la file d’enfants : pendant qu’il égrène les temps de la comptine, il demande à l’enfant en tête de file d’aller se placer derrière. Lorsque la comptine s’achève, l’enfant de tête est éliminé.
Il y a des listes doublement chaînées dans ce sujet de concours :

















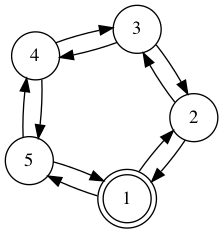







Commentaires