Présentation au séminaire IREMI
Le 30 novembre 2022, cette présentation a été faite au séminaire IREMI :
On y a évoqué les points suivants :
- des entiers relatifs, construits à la Conway, apparaissent dans les fins de parties, parfois comme sommes d’entiers relatifs plus simples,
- la finitude du jeu est prouvable grâce à l’existence d’un variant : le nombre de degrés de liberté des pions, plus le triple du nombre de pions,
- en changeant certains signes dans le variant, on obtient une expression qui n’est plus un variant mais qui peut servir d’heuristique pour un algorithme minimax voire une illustration de l’élagage alpha-bêta...
La contribution de Julien Lemoine
Julien Lemoine, qui a déjà publié d’autres analyses de jeux, a programmé un algorithme de recherche de stratégie gagnante pour l’ancienne version d’alquerkonane (où on avait le droit de reculer un pion).
Le graphe
Le rendu du graphe, effectué par graphviz (et plus précisément la commande dot), est dans ce pdf :
Le graphe est grand parce qu’il contient toutes les positions possibles, sans tenir compte de celle de départ. Il n’est pas si grand que cela parce que tous les sommets identiques à rotation ou symétrie près, sont représentés par un seul d’entre eux.
En cherchant la position de départ NXO··XOXO· (en haut au milieu) on trouve que les noirs ont une stratégie gagnante puisque le sommet est rouge :
En cherchant la position de départ BXO··XOXO· par contre on découvre que si les blancs commencent, ils peuvent arriver à une partie nulle (un sommet blanc fait partie d’un cycle ou peut y mener) :
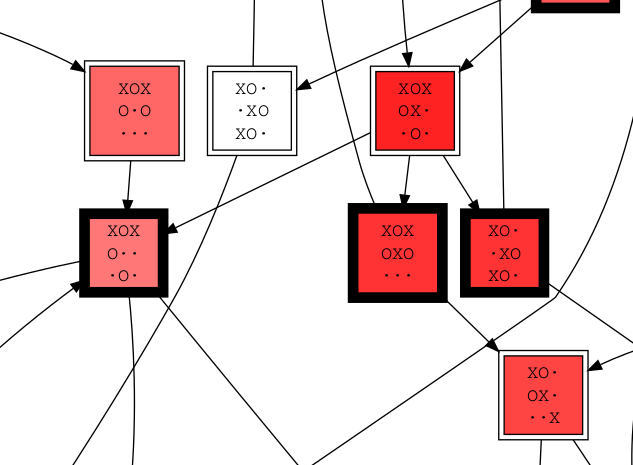
C’est ce constat qui a mené à la restriction des mouvements des pions : comme au jeu de dames, les pions n’ont le droit de reculer que pour prendre.
La contribution de Fabrice Nativel
Elle est ici. On y apprend que
- le jeu alquerkonane 3×3 est positif
- le jeu alquerkonane 4×4 n’est pas un nombre
- le jeu alquerkonane 4×4 à une seule rangée de pions par joueur, est égal à zéro
- le jeu alquerkonane 5×5 est positif
- le jeu alquerkonane 6×6 à une rangée de pions, n’est pas un nombre.
Conjecture : la recherche d’une stratégie gagnante à alquerkonane sur un damier n×n est un problème PSPACE-complet.
Parcours de graphes
Chercher une stratégie gagnante à alquerkonane, revient à chercher un chemin allant de la position de départ jusqu’à une position gagnante. En fait plusieurs chemins sont possibles, et ils forment un arbre couvrant d’une partie du graphe. Pour chercher cet arbre, on peut opter pour un parcours en profondeur d’abord, ou un parcours en largeur d’abord.
En profondeur d’abord
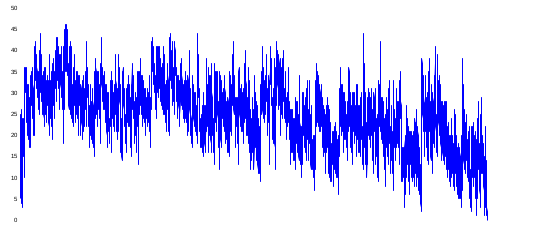
Pour un parcours en profondeur d’abord, les sommets à étudier sont rangés dans une pile (informatique). La hauteur de cette pile évolue de manière assez chaotique au cours du temps :
Mais elle reste de dimension raisonnable (il n’y a jamais plus de 50 sommets à visiter). La hauteur de la pile varie tout de même 33200 fois.
En largeur d’abord
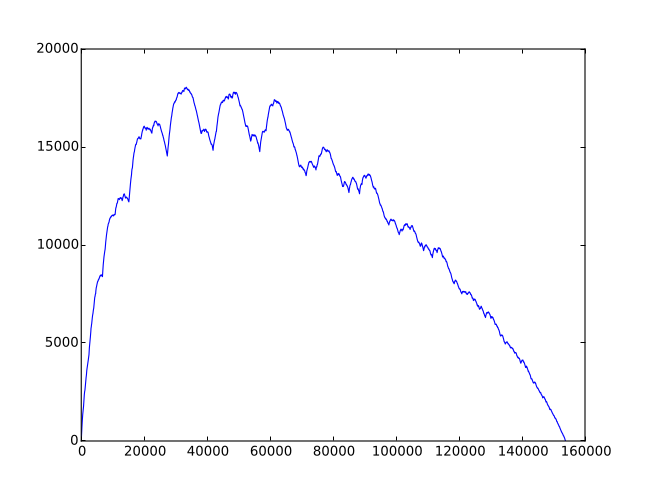
Pour effectuer un parcours du graphe en largeur d’abord, on utilise une file (structure de données). Celle-ci évolue de manière moins chaotique que la pile vue plus haut, mais la taille de la file atteint des valeurs impressionnantes (plus de 18000 sommets à étudier, à certains moments) :
En plus, le nombre de modifications de la file est plus important que pour la pile : environ 5 fois plus, d’après le graphique ci-dessus.
Théorie de Conway
La modélisation par les surréels de Conway permet d’en savoir plus. En particulier, le fait que le jeu alquerkonane 3×3 est positif, ne signifie pas nécessairement que ce soit un nombre positif (des jeux non numériques peuvent également être positifs). Mais on découvre qu’il s’agit du nombre 1 en l’occurrence, ce qui signifie que les noirs peuvent se garantir un minimum d’un mouvement d’avance sur les blancs.
| alquerkonane 2×2 vaut 0 | alquerkonane 3×3 vaut 1 | la fraction -1/2 dans alquerkonane | stratégie gagnante 3×3 |
|
|
|
|
|
On note ci-dessus qu’à alquerkonane 3×3, si les noirs jouent mal, les blancs peuvent avoir un demi-coup d’avance sur les noirs ! Pour en savoir plus sur le formalisme de Conway, voir la carte des cartes.
Conjectures
- La valeur initiale de alquerkonane 4×4 est le jeu que Conway notait ±2 (celui qui commence assure au moins 2 points d’avance sur son adversaire).
- Le jeu alquerkonane sur un damier n×n est PSPACE-difficile.
IA avec ludii
Le logiciel AlphaGo Zero, comme son nom l’indique, est spécialisé dans le jeu de Go. Il a été généralisé en AlphaZero qui gagne aussi aux échecs, et pas seulement au Go. Ces logiciels utilisent des méthodes d’IA qui sont implémentées dans ludii. Ce logiciel, programmé en Java (langage), permet de décrire n’importe quel jeu abstrait connu, à l’aide d’un langage de type Lisp. Par exemple pour y programmer alquerkonane avec des oiseaux et des poissons (les cases claires sont de l’eau ; les oiseaux ne peuvent y aller sinon ils se noient, et les poissons ne peuvent sortir de l’eau que pour sauter par dessus un oiseau ; de même les oiseaux peuvent piétiner les poissons pour aller d’une case noire à une autre orthogonalement), on peut écrire ce script :
(game "alquerkonane"
("TwoPlayersNorthSouth")
(equipment
{
(board (rectangle <Rows:num> <Columns:num>))
(piece "Fish"
P1
(or
(move Step (directions { BL BR }) (to if:(is Empty (to))))
(move
Hop
(between
if:(is Enemy (who at:(between)))
(apply (remove (between)))
)
(to if:(is Empty (to)))
)
)
)
(piece "Goose"
P2
(or
(move Step (directions { BL BR }) (to if:(is Empty (to))))
(move
Hop
(between
if:(is Enemy (who at:(between)))
(apply (remove (between)))
)
(to if:(is Empty (to)))
)
)
)
}
)
(rules
(start
{
(place
"Goose2"
(intersection
(sites Phase 0)
(expand (sites Bottom) steps:1)
)
)
(place
"Fish1"
(intersection
(sites Phase 1)
(expand (sites Top) steps:1)
)
)
}
)
(play (forEach Piece))
(end (if (no Moves Next) (result Mover Win)))
)
)
(option "Rows" <Rows> args:{ <num> }
{
(item "2" <2> "The board has 2 rows.")
(item "3" <3> "The board has 3 rows.")
(item "4" <4> "The board has 4 rows.")*
(item "5" <5> "The board has 5 rows.")
(item "6" <6> "The board has 6 rows.")**
(item "7" <7> "The board has 7 rows.")
(item "8" <8> "The board has 8 rows.")*
(item "9" <9> "The board has 9 rows.")
(item "10" <10> "The board has 10 rows.")
}
)
(option "Columns" <Columns> args:{ <num> }
{
(item "2" <2> "The board has 2 columns.")
(item "3" <3> "The board has 3 columns.")
(item "4" <4> "The board has 4 columns.")**
(item "5" <5> "The board has 5 columns.")
(item "6" <6> "The board has 6 columns.")*
(item "7" <7> "The board has 7 columns.")
(item "8" <8> "The board has 8 columns.")*
(item "9" <9> "The board has 9 columns.")
(item "10" <10> "The board has 10 columns.")
}
)
(metadata
(graphics (board Style Chess))
)Dans le logiciel ludii, ce script donne le rendu suivant :
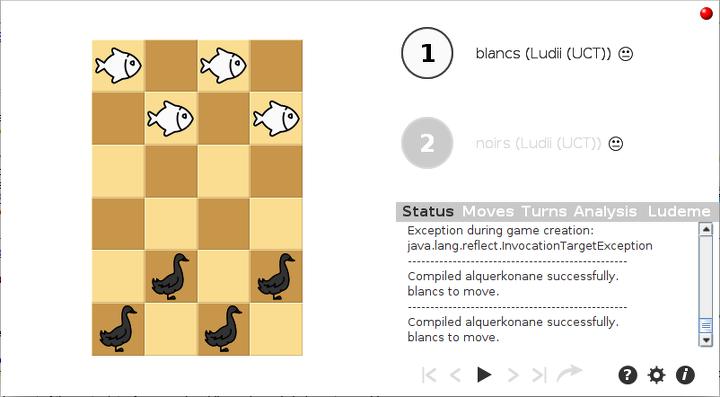
Parmi les IA de ludii, l’élagage alpha-bêta est bien adapté à des jeux de stratégie comme alquerkonane. Mais ci-dessus on lui a préféré l’IA d’AlphaZero (son nom est UCT, c’est une amélioration de MCST qui signifie recherche arborescente Monte-Carlo) qui est plus recommandée pour la tactique (comme aux échecs). En effet alphaBeta ne joue pas de façon optimale : cette IA préfére gagner vite plutôt que gagner beaucoup. Tout le problème est de trouver une fonction d’évaluation.
On propose alors cet enrichissement du jeu : chaque joueur dispose, en plus de ses pions, de jetons, qui lui serviront durant la phase finale du jeu. Le perdant paye le droit de passer son tour en donnant un jeton au gagnant, et ce, jusqu’à ce que le gagnant ne puisse plus bouger non plus. Le nombre de fois que le perdant a passé son tour, est le score du gagnant. Alors on ne cherche plus seulement à bouger plus longtemps que l’adversaire, mais à maximiser le nombre de mouvements.
On utilise la notion de score d’un joueur :
(game "alquerkonane"
("TwoPlayersNorthSouth")
(equipment
{
(board (rectangle <Rows:num> <Columns:num>))
(piece "Ball" Each
(or
(move Step (directions { FL FR }) (to if:(is Empty (to))))
(move
Hop
(between
if:(is Enemy (who at:(between)))
(apply (remove (between)))
)
(to if:(is Empty (to)))
)
)
)
}
)
(rules
(start
{
(set Score Each 0)
(place
"Ball2"
(intersection
(sites Phase 0)
(expand (sites Top) steps:1)
)
)
(place
"Ball1"
(intersection
(sites Phase 1)
(expand (sites Bottom) steps:1)
)
)
}
)
(play
(priority
(forEach Piece)
(move Pass (then
(if (= (score Mover) 0) (addScore Next 1))
))
)
)
(end (if (all Passed) (byScore)))
)
)
(option "Rows" <Rows> args:{ <num> }
{
(item "2" <2> "The board has 2 rows.")
(item "3" <3> "The board has 3 rows.")
(item "4" <4> "The board has 4 rows.")*
(item "5" <5> "The board has 5 rows.")
(item "6" <6> "The board has 6 rows.")**
(item "7" <7> "The board has 7 rows.")
(item "8" <8> "The board has 8 rows.")*
(item "9" <9> "The board has 9 rows.")
(item "10" <10> "The board has 10 rows.")
}
)
(option "Columns" <Columns> args:{ <num> }
{
(item "2" <2> "The board has 2 columns.")
(item "3" <3> "The board has 3 columns.")
(item "4" <4> "The board has 4 columns.")**
(item "5" <5> "The board has 5 columns.")
(item "6" <6> "The board has 6 columns.")*
(item "7" <7> "The board has 7 columns.")
(item "8" <8> "The board has 8 columns.")*
(item "9" <9> "The board has 9 columns.")
(item "10" <10> "The board has 10 columns.")
}
)
(metadata
(graphics (board Style Chess))
(ai
(alphaBeta
(heuristics
(score)
)
)
)
)Mais le score n’étant calculé qu’à la fin, l’ai alphaBeta ne l’utilise pas pour évaluer les positions. D’ailleurs elle joue assez mal à la fin :
- les blancs font leur dernier mouvement :
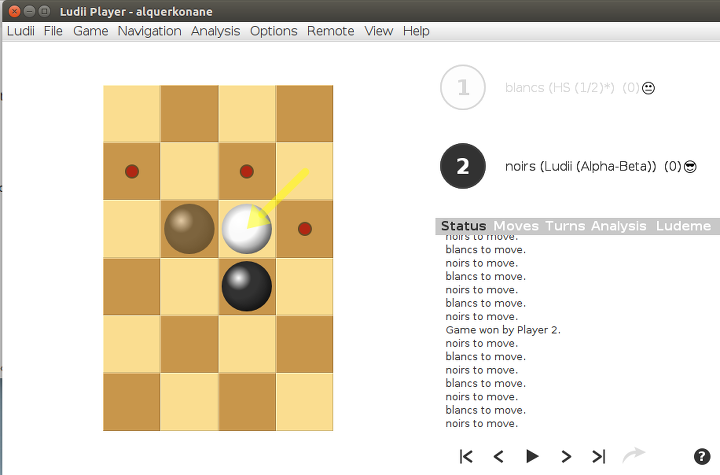
Les petits points en rouge désignent les possibilités de jeu des noirs (il y a un onglet à cocher dans ludii pour activer cet affichage). Le pion noir qui est en B4 peut aller en A5 ou en C5, le pion noir qui est en C3 peut aller en D4 ou en C5, et dans ce dernier cas il prend le dernier pion blanc.
- Les noirs prennent le pion blanc :
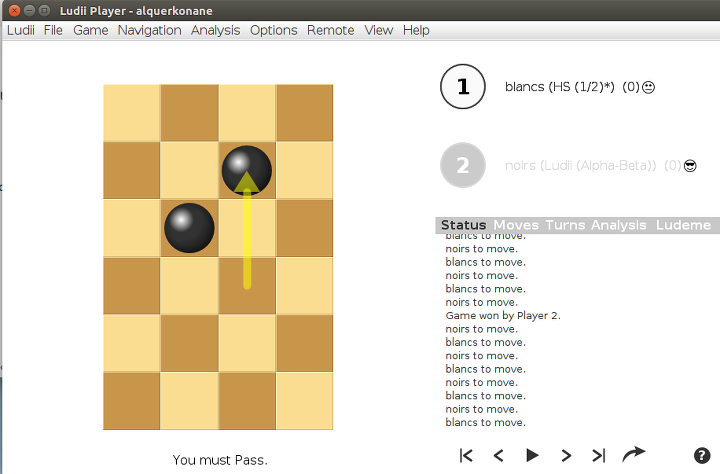
Ils peuvent alors marquer 4 points (le point du gagnant et les trois mouvements vers D6 puis vers A5 puis B6).
- Ils commencent d’abord par la gauche, en amenant en A5 le pion qui était en B4 :
Les blancs ont passé leur tour et donné un point aux noirs (lisible en haut à droite)
- Mais ils bougent le pion qui est en C5 vers la gauche (B6 au lieu de D6) :
Les blancs ne leur donnent donc qu’un second point. Les noirs se sont bloqués eux-mêmes parce que leur algorithme alphaBeta n’a pas daigné calculer le score.
Il faut donc une autre heuristique pour alphaBeta si on veut optimiser le score.
Malgré cela, l’élagage alpha-bêta joue bien et amène à conjecturer que la valeur du jeu sur un damier 4×4 est ±1 plutôt que ±2...
Commentaires