Attention : dans tout l’article, les dessins sont cliquables et permettent d’accéder à des figures dynamiques manipulables en ligne.

1. Introduction

Soit $\mathbb{P}$ un plan affine muni d’une structure métrique au moyen d’une distance $d$ arbitraire, par exemple la distance euclidienne usuelle. La notion de convergence utilisée ici le sera soit au sens de la topologie induite par $d$ sur $\mathbb{P}$ (lorsqu’il s’agit de suites de points), soit au sens de la topologie naturellement induite par $d$ sur le produit cartésien $\mathbb{P}^5$.

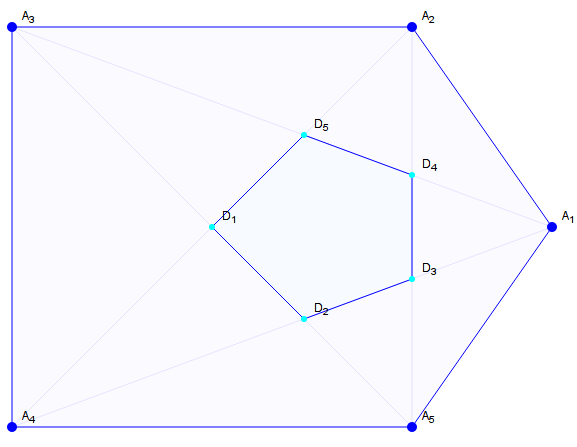
Les cinq diagonales d’un pentagone convexe $\mathcal{P}=A_1 A_2 A_3 A_4 A_5$ de $\mathbb{P}$ se coupent en cinq points formant un pentagone strictement convexe $\mathcal{D}_1$ de sommets $(D_k^{(1)})_{1≤k≤5}$ définis par :

$$ D_1^{(1)}=(A_2 A_4)\cap (A_3 A_5),\ \ D_2^{(1)}=(A_1 A_4) \cap (A_3 A_5),\ \ D_3^{(1)}=(A_2 A_5)\cap (A_1 A_4),\\ D_4^{(1)}=(A_2 A_5) \cap (A_1 A_3),\ \ D_5^{(1)}=(A_2 A_4)\cap (A_1 A_3). $$

Bouger les points bleus dans la figure accessible ci-dessous (éviter de rendre le pentagone concave) pour vérifier cela :

La suite diagopentagonale de $\mathcal{P}$ est la suite de pentagones strictement convexes $(\mathcal{D}_n)_{n \in \mathbb{N}}$ obtenue par la construction récurrente :

$$ \left\{ \begin{aligned} &\mathcal{D}_0=\mathcal{P}\quad (\forall k \in ⟦1 ;5⟧,\ D_k^{(0)}=A_k)\\ &\mathrm{Pour\ tout}\ n\in \mathbb{N},\, \mathcal{D}_{n+1}=(D_k^{(n+1)})_{1≤k≤5}\ \mathrm{est\ le\ diagopentagone\ de}\ \mathcal{D}_n=(D_k^{(n)})_{1≤k≤5}. \end{aligned} \right. $$

Bouger les points bleus dans la figure accessible ci-dessous (éviter de rendre le pentagone concave) pour vérifier cela :

Le problème considéré est alors celui de la convergence de la suite ainsi définie.

2. Représentation canonique d’un pentagone strictement convexe

Proposition 1 de l’article [2]

Soit $A_2 A_3 A_4 A_5$ un carré de centre $O$. On munit le plan projectif du repère $\mathcal{R}$ centré en $O$ et d’axes parallèles à ses côtés, dans lequel $A_2(1 ;1)$, $A_3(-1 ;1)$, $A_4(-1 ;-1)$ et $A_5(1 ;-1)$.

Pour tout pentagone strictement convexe $\mathcal{P}=B_1 B_2 B_3 B_4 B_5$, il existe une unique homographie $t$ qui transforme $B_k$ en $A_k$ pour tout $k \in ⟦2 ;5⟧$.

Soient $A_1=t\,(B_1)$ et $\mathcal{P}’$ le pentagone $A_1 A_2 A_3 A_4 A_5$. Alors t transforme $\mathcal{P}$ en $\mathcal{P}’$ et il existe un unique couple $(x ;y)\in\,]0 ;+\infty[\, \times\, ]-1 ;1[$ tel que $A_1 (1+x\, ;y)$ dans le repère $\mathcal{R}$.

On dit que $\mathcal{P}’$, muni de $\mathcal{R}$, est le pentagone canonique associé à $\mathcal{P}$. Et on appelle $(x ;y)$ les paramètres de cette représentation.

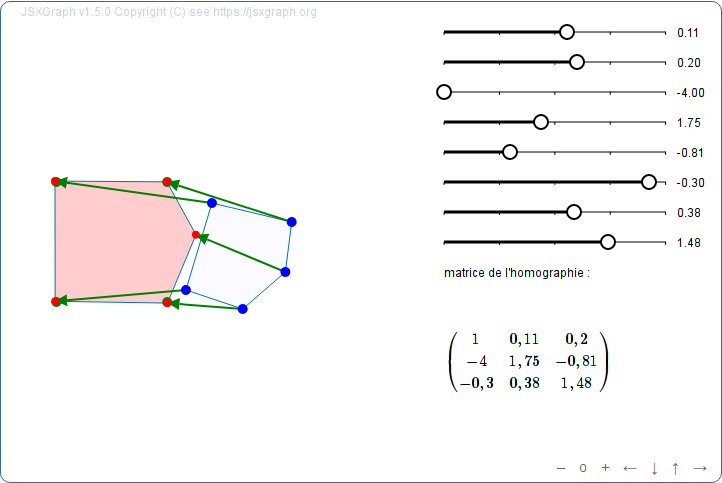
Pour se détendre un peu, on propose maintenant une petite pause ludique, avec ce jeu en ligne, où il s’agit justement de trouver l’homographie transformant le pentagone (bleu) en pentagone (rouge) canonique :

Ce jeu permet, de par sa difficulté, de constater qu’une homographie n’a rien d’intuitif.

3. Homographies diagopentagonales

Proposition 2 de l’article [2] et définition

Il existe pour tout pentagone strictement convexe $\mathcal{P}$ une unique homographie $h$ qui transforme les sommets de $\mathcal{P}$ en les sommets correspondants de son diagopentagone et cette même homographie transforme chaque sommet de tout pentagone $\mathcal{D}_n$ de la suite diagopentagonale de $\mathcal{P}$ en le sommet correspondant du diagopentagone $\mathcal{D}_{n+1}$ de $\mathcal{D}_n$.

On appellera ici $h$ l’homographie diagopentagonale de $\mathcal{P}$.

4. Convergence et limite d’une suite diagopentagonale

Proposition 6 de l’article [2]

Soit $h_{x ;y}$ l’homographie diagopentagonale d’un pentagone canonique de paramètres $(x ;y)\in \Delta =\,]0 ;+\infty[ \,\times\, ]-1 ;1[$.

À l’exception du cas $(x ;y)=\left(\dfrac{\sqrt{5}-1}{2} ;0\right)$, $h_{x ;y}$ a trois points fixes distincts dont l’un est à l’infini si $y=0$.

Dans l’unique cas $(x ;y)=\left(\dfrac{\sqrt{5}-1}{2} ;0\right)$, qui correspond canoniquement au pentagone régulier, il existe une droite de points fixes extérieurs au pentagone initial, celle formée des points de coordonnées $(2+\sqrt{5} ;\beta)$ où $\beta \in \mathbb{R}$, et un unique point fixe isolé qui est intérieur au pentagone initial, celui de coordonnées $\left(\dfrac{\sqrt{5}-1}{2} ;0\right)$.

La figure dynamique suivante montre le cas où l’ordonnée est nulle :

et celle-ci le cas général (trois points fixes) :

Proposition 7 de l’article [2]

L’homographie diagopentagonale de tout pentagone strictement convexe $\mathcal{P}$ a un unique point fixe $\Omega$ intérieur à $\mathcal{P}$.

La figure dynamique ci-jointe dessine aussi ces trois points fixes, coloriés respectivement en vert (celui qui est dans le pentagone), bleu et rouge. Mais cette fois-ci, pas de triangle et les traces des points sont activées, ce qui permet de voir le lieu des points fixes lorsque le sommet à droite du pentagone parcourt la représentation graphique de la fonction $\frac{1}{x}$ sur $[1 ;+\infty[$ :

Il est possible de modifier la fonction, pour obtenir d’autres lieus (penser à zoomer-dézoomer pour effacer les traces précédentes). Attention toutefois à ce que les ordonnées de la courbe soient comprises entre -1 et 1 (sinon le pentagone n’est plus convexe et les points fixes cessent d’exister).

Théorème de l’article [2]

La suite diagopentagonale de tout pentagone strictement convexe $\mathcal{P}$ converge vers l’unique point fixe $\Omega$ de son homographie diagopentagonale qui est intérieur à $\mathcal{P}$.

On pourra appeler $\Omega$ le centre diagonal de $\mathcal{P}$.

5. Généralisation du problème

On peut envisager de généraliser la présente étude à tout polygone $\mathcal{P}=A_1 A_2 \dots A_n$ strictement convexe dont le nombre $n$ de côtés dépasse 5. L’enveloppe convexe de l’ensemble des points d’intersection intérieurs à $\mathcal{P}$ est un $n$-gone strictement convexe $\mathcal{P}’$ qu’on peut appeler le diagopolygone de $\mathcal{P}$. Ceci permet de définir par récurrence la suite diagopolygonale de $\mathcal{P}$. Reste à savoir dans ce cas généralisé quel est le comportement asymptotique de cette suite...