Points pondérés

On commence par construire les points A, B et C auxquels on donne les coordonnées (0 ;6), (2 ;0) et (4 ;6). CaRMetal possédant des macros pour la création de barycentres, on va évidemment les utiliser. Mais les masses de A, B et C dépendant de t, il faut d’abord créer t...

Celui-ci variant dans un intervalle, sera matérialisé par un curseur. Mais par la suite on voudra tracer un lieu dépendant de t, on va utiliser un curseur « expert ». Dans les « macros expert », ce curseur s’appelle « curseur linéaire continu », et on l’a placé ci-dessous dans la partie en bas à gauche :

Quelques modifications ont été apportées à ce curseur (dont les valeurs extrêmes ont été mises à 0 et 1) : Les valeurs extrêmes et les points d’ancrage ont été rendus invisibles, et l’expression a été renommée t pour usage ultérieur.

Ensuite la macro « point pondéré » a été utilisée quatre fois :

• A et 1-t
• B et t
• B et 1-t
• C et t

Comme B a été pondéré deux fois, il a fallu déplacer l’un de ses deux coefficients (remplacer x(B)+0,2 par x(B)-1,2).

Barycentres

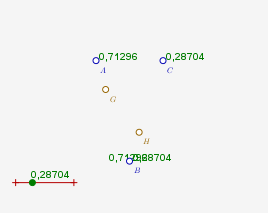
La macro « barycentre 2 pts » a servi à construire G et H ci-dessus (en marron).

Ensuite G et H ont été pondérés avec la macro "point pondéré :

ce qui a permis de construire M avec la macro « barycentre 2 pts ». Manipuler la curseur ci-dessus pour voir comment évoluent les barycentres G, H et M.

Lieu

Pour finir le TP, il ne reste plus qu’à :

• gommer les points G et H et les coefficients (pour ne pas alourdir la figure),
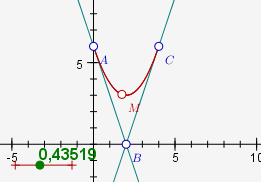
• construire les deux droites (AB) et (AC) avec l’outil « droite »(en cyan ci-dessous),
• Construire la courbe (en rouge ci-dessous) avec l’outil « lieu » (cliquer sur M et ensuite, double-cliquer sur le point vert du curseur.

Comme l’indique le titre du sujet, on vient de construire une courbe de Bézier [1].