DNB
Cet exercice a été donné au DNB de 2022 (en Polynésie) :
On considère le programme de calcul suivant :
1. a. Si on choisit le nombre 7, vérifier qu’on obtient 49 à la fin du programme
b. Si on choisit le nombre −4, quel résultat obtient-on à la fin du programme ?
2. On note x le nombre choisi au départ
a. Exprimer en fonction de x le résultat obtenu.
b. Développer et réduire (x + 5)(x − 5).
c. Sarah dit : « Avec ce programme de calcul, quel que soit le nombre choisi au départ, le résultat obtenu est toujours le carré du nombre de départ ».
Qu’en pensez-vous ?
flow974
On peut répondre aux premières questions en reproduisant le diagramme du sujet sur flow974.
Voici la version du sujet :
Et celle obtenue sur flow974 :
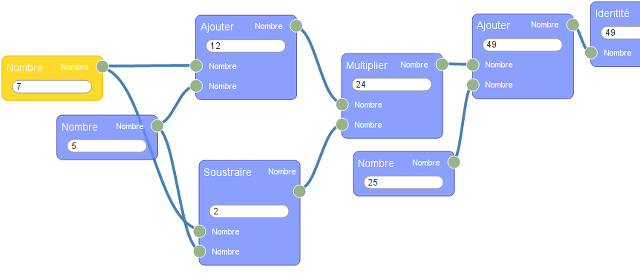
En mettant le premier nombre (en haut à gauche) sur 7, on vérifie (en haut à droite) que le résultat est bien 49. Et en mettant le nombre choisi sur -4
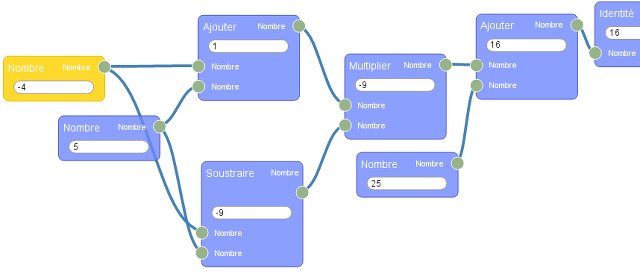
on trouve que le résultat est 16 (qui est bien, comme le prétend Sarah, le carré de -4).
La programmation par flot permet de faire abstraction du fait qu’il y a deux modifications à apporter (augmenter de 5, diminuer de 5). En Python, il faut garder une copie de la valeur initiale du nombre choisi (ou, ce qui revient au même, une autre variable) pour mémoriser cette valeur initiale. On montre dans les onglets suivants comment faire.
Sofus
Pour traduire en Python, on peut utiliser SofusPy974 où on crée une copie qu’on modifie en place :
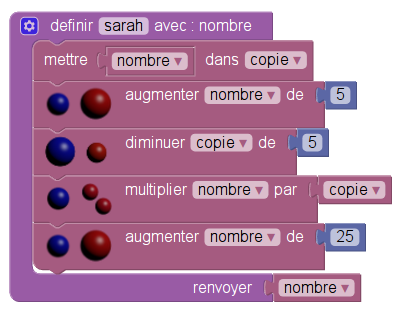
SofusPy974 est doté d’un bouton Python, (appelé éditeur) à cliquer pour obtenir automatiquement ce script :
def sarah(nombre):
copie = nombre
nombre = nombre + 5
copie = copie - 5
nombre = nombre * copie
nombre = nombre + 25
return nombrePour répondre aux questions de l’exercice, on entre dans une console
>>> sarah(7)
49
>>> sarah(-4)
16
>>>Mais cela ne permet pas de prouver l’affirmation de Sarah. Pour une preuve utilisant directement le calcul formel, on peut utiliser Sofus (sans Python), qui permet de manipuler aussi des expressions littérales :
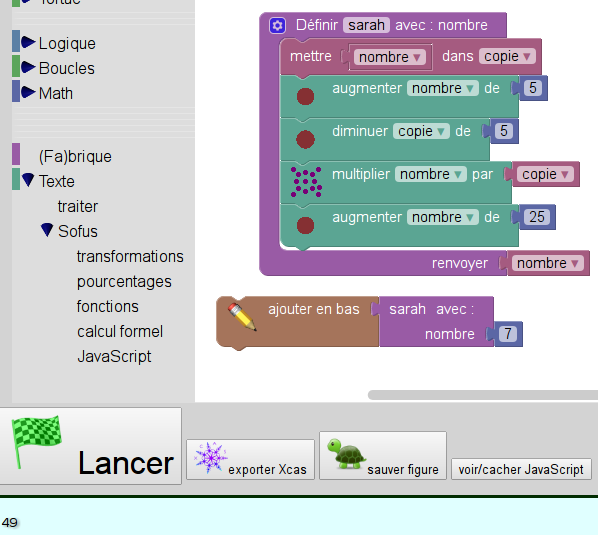
On voit dans l’affichage en bas que l’image de 7 par la fonction est 49. Pour avoir l’image de x par cette fonction, il suffit de remplacer 7 par x :
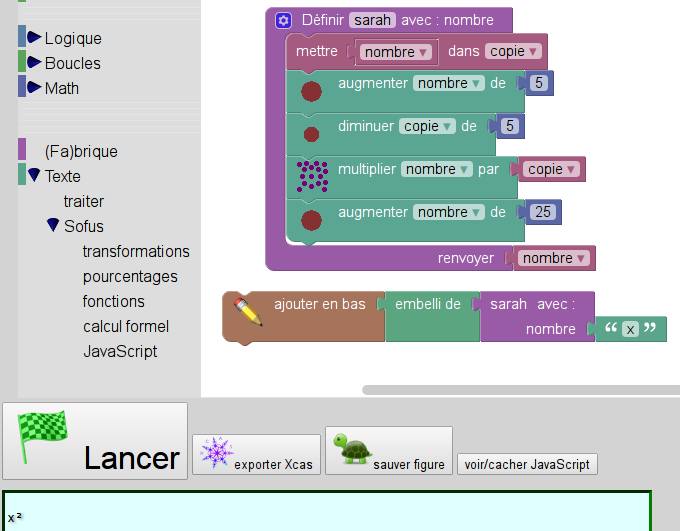
Ceci prouve l’affirmation de Sarah. Mais sans expliquer pourquoi. On verra plus loin que why3 fait pareil, malgré ce que son nom laisse penser : il donne un certificat sans qu’on aie besoin de vérifier pourquoi. On va donc aider Sarah à obtenir ce certificat, en programmant sa fonction en Python puis en la soumettant à why3.
Python
Sarah programme sa fonction en Python. En voyant le schéma
elle décide de créer deux nouvelles variables, correspondant aux deux facteurs du produit. Elle appelle facteur1 celle qui est à gauche et facteur2 celle qui est à droite :
def sarah(nombre):
facteur1 = nombre+5
facteur2 = nombre-5
produit = facteur1 * facteur2
return produit+25On peut alors vérifier, en mode pas-à-pas, sur Pythontutor :
Mais cela ne prouve pas l’affirmation de Sarah dans tous les cas. C’est là que why3 entre en scène.
why3
L’affirmation de Sarah est simplement un commentaire dans le script Python :
def sarah(nombre):
#@ ensures result == nombre*nombre
facteur1 = nombre+5
facteur2 = nombre-5
produit = facteur1 * facteur2
return produit+25Mais ce commentaire débute par un arobase, ce qui lui donne un sens pour why3. Le mot-clé result désigne ce qui est renvoyé par la fonction. En copiant ce script sur le site de why3 on a
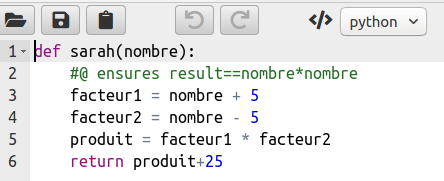
Pour demander une certification de la fonction, il suffit alors de cliquer sur la baguette magique et why3 s’occupe du reste :
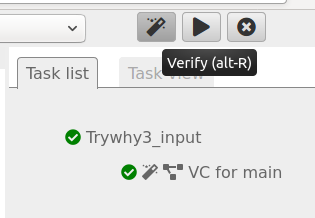
Mais malgré son nom, why3 se contente de donner un certificat : Sarah a raison, et n’explique pas pourquoi elle a raison. Pour en savoir un peu plus, on peut cliquer sur l’icône représentant un arbre, ce qui a pour effet de séparer le but à prouver en sous-buts :

On en sait maintenant plus : si l’affirmation de Sarah est vraie, c’est parce qu’elle correspond à une postcondition et c’est une postcondition que why3 a prouvé.
Pour prouver une postcondition sur une fonction Python, on ajoute au début de la définition de cette fonction, un commentaire de ce genre :
#@ ensures la_condition
où la_condition est un booléen de Python, puis on copie le script sur why3 en Python et on clique sur la baguette magique.
Post
Pour initier les élèves de 1re aux variants et invariants dès le début de l’année scolaire, il est intéressant de les mettre en œuvre sur des exemples simples, autrement dit, portant sur des types de base (entiers naturels par exemple).
L’exemple des machines à registre, déjà testé avec succès dans le premier degré, s’avère parfait pour cela.

L’activité a été pratiquée tout d’abord en mode débranché (il s’agissait de tester les programmes et émettre des conjectures sur le résultat de l’opération).
Listes
En fait les registres de la machine à registre sont groupés en un tableau d’entiers. Pour modéliser en Python un tel tableau, on utilise des variables numérotées. Par exemple
L = [5,0,3,2]
ce qui revient (une fois L de longueur suffisante) à
L[0] = 5
L[1] = 0
L[2] = 3
L[3] = 2qu’au début de l’année de 1re on notera
L0 = 5
L1 = 0
L2 = 3
L3 = 2Ceci aura l’avantage d’éviter de demander à why3 de vérifier que des indices sont bien entre les bornes.
Plus tard on apprend à dessiner un tableau d’entiers naturels avec cette fonction :
def dessiner(tab):
for n in tab:
print(n*'o')Par exemple avec
dessiner( [5,0,3,2] )
on a dans la console
ooooo
ooo
ooAddition
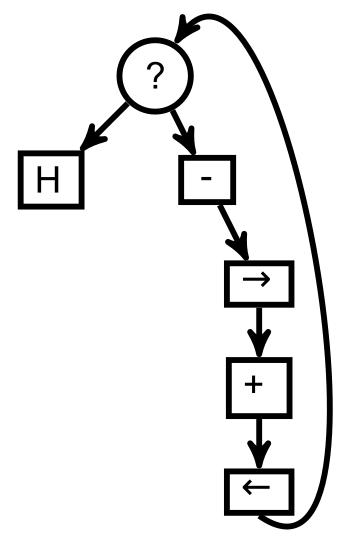
Le programme d’addition pour la machine à registres (avec seulement L0 et L1 utilisés, le doigt pointant initialement vers L0) est
La première étape est de traduire ce programme en Python.
Tout d’abord, le point d’interrogation en haut mène à
- un arrêt (sortie de boucle) à gauche, si la première case est vide (L0==0)
- une boucle (très visible sur la partie droite du graphe) sinon.
En effet dans la boucle, il y a un aller-retour du doigt vers la case L1. C’est bien la non nullité de L0 qui est testée à chaque retour de la boucle.
Le début du script ressemblera donc à
def addition(a,b):
L0 = a
L1 = b
while L0>0:Reste à détailler ce qu’on fait dans la boucle :
- on enlève une graine de la première case : L0 -= 1
- on déplace le doigt vers la droite : maintenant c’est sur la variable L1 qu’on va opérer
- on sème une graine devant le doigt : L1 += 1
- on ramène le doigt vers la gauche : on boucle bien sur L0
Ce qui donne alors ce script :
def addition(a,b):
L0 = a
L1 = b
while L0>0:
L0 -= 1
L1 += 1
return L1Comment sait-on que c’est L1 qui contient le résultat de l’addition ? On l’a constaté expérimentalement lors de la phase débranchée de l’activité.
Pour faire certifier qu’il s’agit bien d’une addition, on modifie le script ainsi :
def addition(a,b):
#@ ensures result==a+b
L0 = a
L1 = b
while L0>0:
L0 -= 1
L1 += 1
return L1puis on va sur le site why3 (paramétré en Python) et on demande la vérification en cliquant sur la baguette magique.
La magie n’opère pas : why3 ne réussit pas à prouver qu’il s’agit bien d’une addition. On voit d’ailleurs que ce n’est pas le seul problème : why3 a également échoué à prouver que l’algorithme se termine !
En ce qui concerne la terminaison, il est impossible de la prouver, parce que l’algorithme ne termine pas !
En effet si on essaye avec des nombres négatifs la condition L0==0 ne sera jamais atteinte.
Ce problème aura plus de chances d’être résolu :
def addition(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a+b
L0 = a
L1 = b
while L0>0:
L0 -= 1
L1 += 1
return L1Mais cela ne suffit toujours pas : pour prouver la terminaison de l’algorithme, why3 a besoin d’un variant. C’est le moment de définir un variant (en 1re) :
Un variant est une expression à valeur entière positive qui décroît strictement à chaque passage dans la boucle
why3 doit vérifier
- que l’expression proposée est bien un variant
- qu’elle a une valeur positive au début
et en déduira la terminaison de la boucle, et donc de l’algorithme.
Un variant tout trouvé est la variable L0 qui décroît à chaque passage dans la boucle :
def addition(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a+b
L0 = a
L1 = b
while L0>0:
#@ variant L0
L0 -= 1
L1 += 1
return L1Maintenant why3 réussit à certifier la terminaison de l’algorithme [2] :
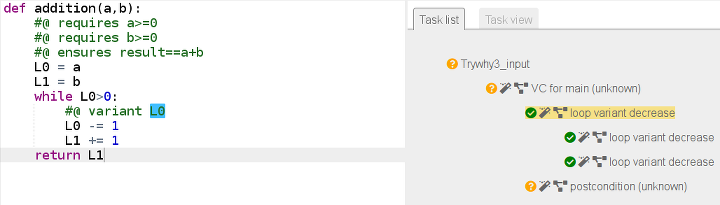
Pour prouver la correction, il faut un invariant. C’est le moment de définir cette notion :
Un invariant est un booléen qui garde la même valeur après chaque passage dans la boucle
Alors si l’invariant s’évalue à True avant d’entrer dans la boucle, il sera True à la sortie de la boucle. Des exemples d’invariants sont proposés :
2+2==4
a>=0
b>=0
L0>=0
L1>=0
L0+L1==a+bmais seul le dernier a quelque utilité dans le cas présent :
def addition(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a+b
L0 = a
L1 = b
while L0>0:
#@ variant L0
#@ invariant L0+L1==a+b
L0 -= 1
L1 += 1
return L1Mais ça ne suffit toujours pas :
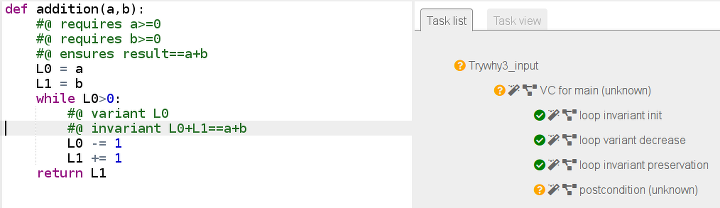
Selon why3, le booléen L0+L1==a+b est bien un invariant, mais il ne sert à rien si on ne peut pas prouver qu’il est vrai au début du script. Or, au début, les variables L0 et L1 sont initialisées à a et b donc L0+L1 est censé valoir a+b. Où est le problème ?
Il semble que why3 utilise un raisonnement par récurrence et on a besoin de prouver que le variant L0 est positif :
def addition(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a+b
L0 = a
L1 = b
while L0>0:
#@ variant L0
#@ invariant L0>=0
#@ invariant L0+L1==a+b
L0 -= 1
L1 += 1
return L1Ce script donne le certificat tant attendu (et mérité, après toutes ces pérégrinations !) :
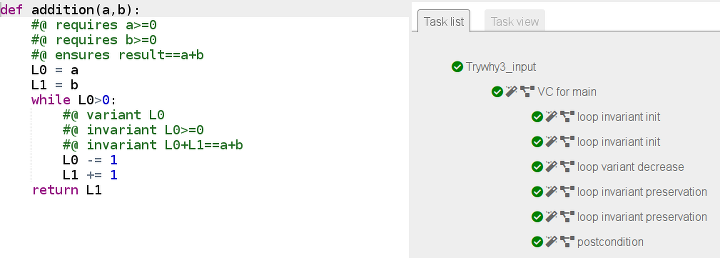
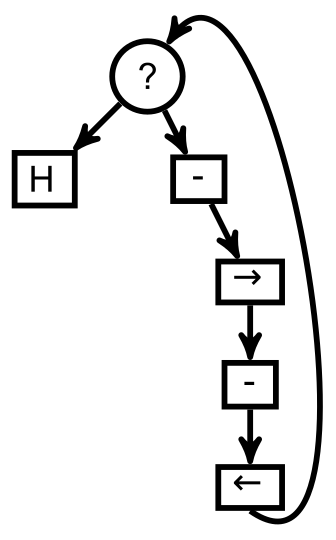
Soustraction
L’algorithme de soustraction ressemble beaucoup à celui de l’addition :
En fait, la seule différence est qu’au lieu de semer une graine dans la seconde case, on en récolte une. Il suffit donc de remplacer un « + » par un « - » dans le script de l’onglet précédent :
def soustraction(a,b):
L0 = a
L1 = b
while L0>0:
L0 -= 1
L1 -= 1
return L1Ceci dit, il y a quand même une différence importante par rapport au cas de l’addition : tout élève de cycle 2 sait qu’on ne peut pas soustraire à un entier naturel, un entier plus grand que lui. On a donc besoin d’une précondition supplémentaire ici, à savoir que a est inférieur ou égal à b.
Le script proposé à why3 sera donc :
def soustraction(a,b):
#@ requires a>=0
#@ requires b>=0
#@ requires a<=b
#@ ensures result==b-a
L0 = a
L1 = b
while L0>0:
#@ variant L0
#@ invariant L0>=0
#@ invariant L0<=L1
#@ invariant L1-L0==b-a
L0 -= 1
L1 -= 1
return L1Ce script est certifié :
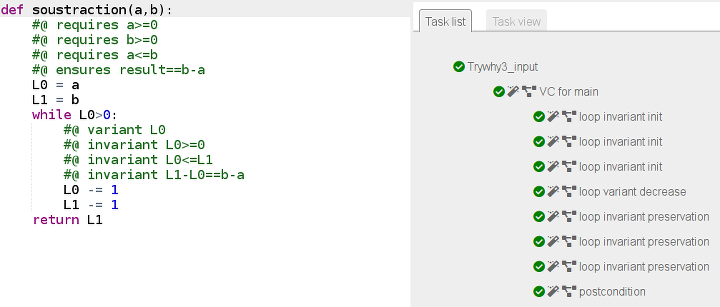
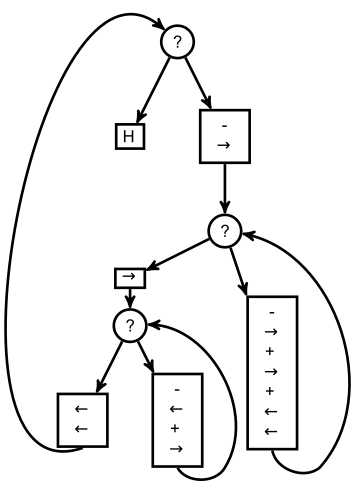
Multiplication
L’algorithme de multiplication est plus complexe, ne serait-ce que parce qu’il utilise plus de registres (4 au lieu de 2 pour les onglets précédents) :
En suivant les mouvements du doigt entre les points d’interrogation, et partant du fait qu’au début le doigt est tout à gauche, on voit que les boucles portent respectivement sur L0, L1 et L2. La structure générale du programme est
def multiplication(a,b):
L0 = a
L1 = b
L2 = 0
L3 = 0
while L0>0:
...
while L1>0:
...
while L2>0:
...
....
return L3On sait que c’est L3 qui contient le produit à la fin, parce qu’on l’a constaté expérimentalement. La suite, c’est de le faire certifier par why3. Comme il y a 3 boucles, on aura a priori besoin de 3 variants.
En lisant les flèches du graphe, on repère quels sont les registres à incrémenter ou décrémenter, ce qui donne cette fonction :
def multiplication(a,b):
L0 = a
L1 = b
L2 = 0
L3 = 0
while L0>0:
L0 -= 1
while L1>0:
L1 -= 1
L2 += 1
L3 += 1
while L2>0:
L2 -= 1
L1 += 1
return L3Les élèves écrivent cela dans un IDE Python, tandis que le graphe est projeté : ils traduisent depuis le graphe, vers le code Python.
Ce script est simplifiable. Par exemple on reconnaît dans la boucle sur L2, l’algorithme d’addition qui a déjà été certifié deux onglets auparavant. Alors on peut remplacer la boucle par la fonction :
def multiplication(a,b):
L0 = a
L1 = b
L2 = 0
L3 = 0
while L0>0:
L0 -= 1
while L1>0:
L1 -= 1
L2 += 1
L3 += 1
L1 += L2
L2 = 0
return L3La dernière ligne vient de ce que l’addition détruit le premier opérande (le rend égal à 0). Mais du coup, la variable L2 qui est initialisée à 0, puis remise à 0 après chaque passage dans le boucle sur L1, devient inutile. Ce qui simplifie encore le script :
def multiplication(a,b):
L0 = a
L1 = b
L3 = 0
while L0>0:
L0 -= 1
while L1>0:
L1 -= 1
L3 += 1
return L3Et maintenant, on reconnaît une nouvelle fois l’algorithme d’addition, dans la boucle sur L1. Ce qui permet une nouvelle simplification du script :
def multiplication(a,b):
L0 = a
L1 = b
L3 = 0
while L0>0:
L0 -= 1
L3 += L1
return L3C’est cette dernière version qui a été testée sur why3 :
def multiplication(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a*b
L0 = a
L1 = b
L3 = 0
while L0>0:
#@ variant L0
#@ invariant L0>=0
#@ invariant L0*b+L3==a*b
L0 -= 1
L3 += L1
return L3Elle est certifiée :
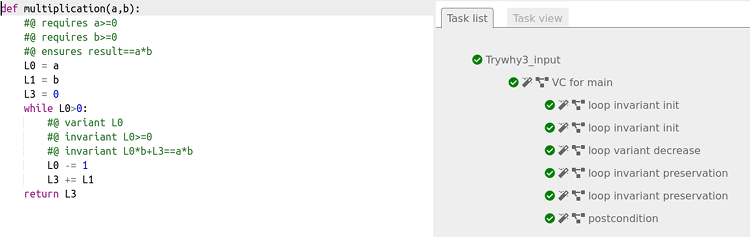
Remarque : On pouvait encore simplifier la fonction, en constatant que la variable L1 n’est pas utile non plus :
def multiplication(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a*b
L0 = a
L3 = 0
while L0>0:
#@ variant L0
#@ invariant L0>=0
#@ invariant L0*b+L3==a*b
L0 -= 1
L3 += b
return L3Cette nouvelle version est également certifiée :
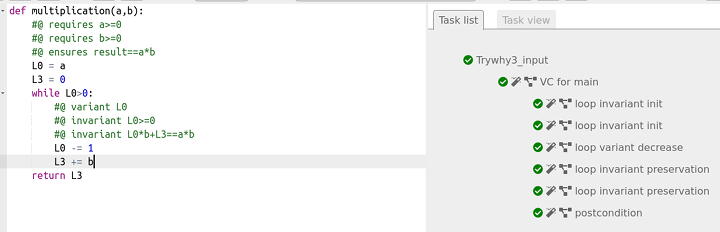
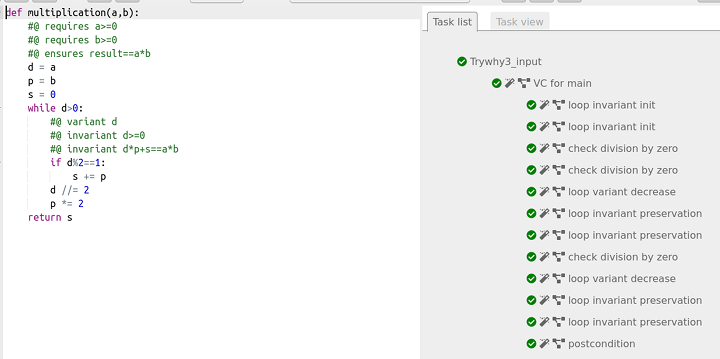
Cette simplification n’a pas été faite en classe (manque de temps) mais un devoir a suivi, portant sur la multiplication éthiopienne :
def multiplication(a,b):
#@ requires a>=0
#@ requires b>=0
#@ ensures result==a*b
d = a
p = b
s = 0
while d>0:
#@ variant d
#@ invariant d>=0
#@ invariant d*p+s==a*b
if d%2==1:
s += p
d //= 2
p *= 2
return sCe « nouvel » [3] algorithme de multiplication est également certifié :
Division
L’algorithme de division par soustraction itérée est certifié également par why3 :
def division(a,b):
#@ requires a>=0
#@ requires b>0
#@ ensures result[1]>b
#@ ensures result[1]>=0
#@ ensures b*result[0]+result[1]==a
L = [0,a]
while L[1]>=b:
#@ variant L[1]
#@ invariant L[1]>=0
#@ invariant b*L[0]+L[1]==a
L[1] -= b
L[0] += 1
return LOn constate qu’il est nécessaire que le diviseur b soit non nul : la division par 0 ne termine pas.
En résumé, why3 est un bureaucrate : on a besoin qu’il donne un coup de tampon pour certifier un algorithme, et lui il réclame d’abord qu’on lui fournisse des formulaires venant de 3 autres bureaux :
- le bureau des variants (entiers décroissants)
- le bureau des invariants (booléens croissants)
- le bureau des postconditions (ensures)
- et parfois le bureau des restrictions (requires)
Un peu comme ici :
On peut réinvestir les variants et invariants dans la suite du cours, à propos des listes de Python.
Listes
Que dit le programme ?
| Contenus | Capacités attendues | Commentaires |
| Parcours séquentiel d’un tableau | Écrire un algorithme de recherche d’une occurence [...] Écrire un algorithme de recherche d’un extremum, de calcul d’une moyenne. |
On montre que le coût est linéaire |
Pas le moindre variant ni invariant ici. Mais comme on en aura besoin plus bas, autant les regarder déjà ici.
in
La recherche d’une occurence peut être comprise de plusieurs manières :
- dire si elt est dans le tableau
- dire où (à quel indice ou quels indices) elt est dans tab
- dire combien de fois elt est dans tab
- dire quels sont les éléments de tab vérifiant un prédicat donné (par exemple extraire les nombres pairs du tableau).
Toutes ces variantes sont présentes à l’épreuve pratique Python du bac NSI.
Dans le paradigme map-filter-reduce il s’agit d’un filtrage. Plus précisément, pour tester si elt est dans tab,
- on effectue un filtrage (tester le prédicat « est égal à elt » sur tab avec
[x for x in tab if x==elt], - puis on réduit avec l’opération or :
any([x==elt for x in tab])
Pour tester si elt est dans tab, on pense à une boucle de ce genre :
def est_dedans(elt,tab):
for x in tab:
if x==elt:
return True
return FalseComme le nombre de passages dans une boucle for est prédéterminé (donc fini), il n’y a pas besoin de prouver la terminaison de l’algorithme. Il n’y a donc que la correction à prouver. Par exemple avec l’affirmation selon laquelle le résultat est True si et seulement s’il existe un indice i tel que l’élément d’indice i dans tab est égal à l’élément cherché :
def est_dedans(elt,tab):
#@ ensures result <-> exists i. 0<=i<=len(tab) and tab[i]==elt
for x in tab:
if x==elt:
return True
return FalseMais why3 ne peut pas certifier cet algorithme :
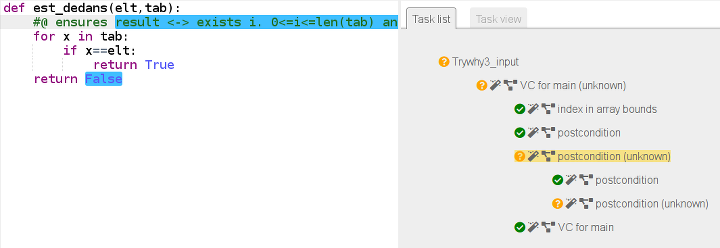
Il lui manque un invariant. Le problème est d’en exprimer un. Celui qui vient naturellement à l’esprit est « on n’a pas encore trouvé elt dans la partie de tab déjà parcourue ». Ne voyant pas comment exprimer cet invariant, on va tout traduire en terme d’indices [4]. La nouvelle version est
def est_dedans(elt,tab):
#@ ensures result <-> exists i. 0<=i<=len(tab) and tab[i]==elt
for i in range(len(tab)):
if tab[i]==elt:
return True
return FalseComme prévu why3 ne prouve pas la correction puisqu’il n’a pas d’invariant à se mettre sous la dent :
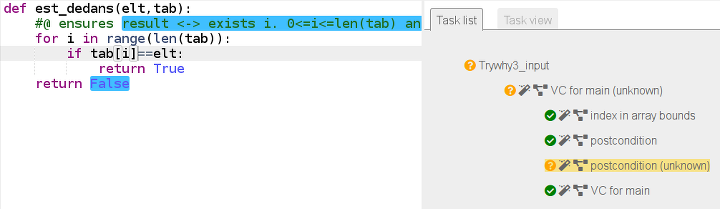
Mais maintenant on peut exprimer en Python l’invariant :
def est_dedans(elt,tab):
#@ ensures result <-> exists i. 0<=i<len(tab) and tab[i]==elt
for i in range(len(tab)):
#@ invariant forall k. 0<=k<i -> tab[k]!=elt
if tab[i]==elt:
return True
return FalseMaintenant why3 certifie l’algorithme :
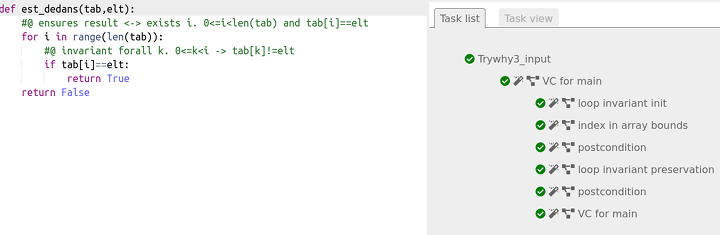
max
Le maximum d’une liste (d’objets munis d’une relation d’ordre, ici des entiers naturels) s’obtient en utilisant la fonction reduce du trio map-filter-reduce avec l’opération (associative) qui, à deux entiers, associe le plus grand des deux. On convient donc que le maximum d’une liste vide est l’élément neutre de cette opération, à savoir 0 (pour les entiers naturels : on utilise le fait que la relation d’ordre sur les entiers naturels est un bon ordre [5] et que le plus petit entier naturel est 0). La variable m sera donc initialisée à 0.
L’expérience acquise dans l’onglet précédent amène à choisir un parcours de la liste par indice :
def maximum(L):
#@ requires forall i. 0<=i<len(L) -> L[i]>=0
#@ ensures forall i. 0<=i<len(L) -> result>=L[i]
m = 0
for k in range(len(L)):
if L[k]>m:
m = L[k]
return mEn fait dire que la valeur finale de m est le maximum, c’est dire que
- d’une part aucun élément de la liste n’est plus grand que m (le ensures ci-dessus)
- d’autre part que cette valeur est bien dans la liste. On ne le prouve pas ici parce que cela a été vu dans l’onglet précédent.
On s’en doutait, why3 n’arrive pas à prouver la correction :
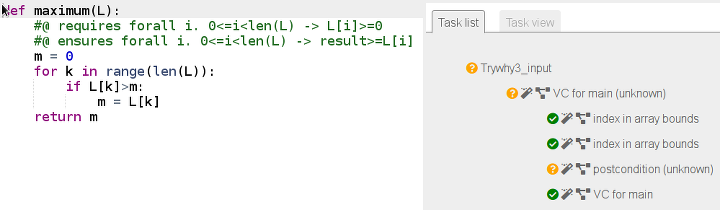
Le problème est de trouver un invariant. Par exemple celui-là :
def maximum(L):
#@ requires forall i. 0<=i<len(L) -> L[i]>=0
#@ ensures forall i. 0<=i<len(L) -> result>=L[i]
m = 0
for k in range(len(L)):
#@ invariant forall i. 0<=i<k -> L[i]<=m
if L[k]>m:
m = L[k]
return mAvec cet invariant, why3 certifie l’algorithme :
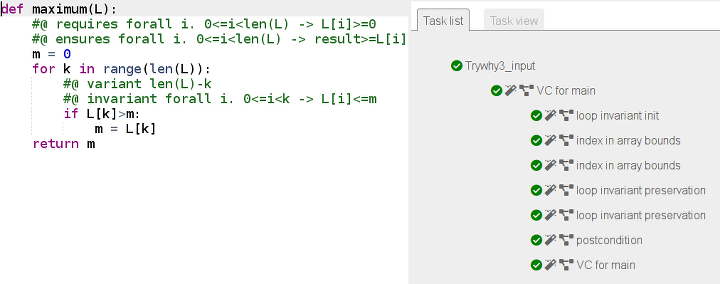
min
La valeur initiale 0 était adaptée pour calculer le maximum d’une liste d’entiers naturels, parce qu’aucun entier naturel n’est plus petit que 0. Pour le minimum d’une liste, on ne peut pas faire pareil : l’élément neutre du minimum est +∞ qui, en Python, est un flottant.
Mais sous réserve que la liste ne soit pas vide, on pouvait également initialiser la variable m au premier élément de la liste [6]. On est donc obligé de préciser que cette nouvelle fonction ne s’applique qu’à des listes non vides (c’est-à-dire de longueur strictement positive) :
def maximum(L):
#@ requires forall i. 0<=i<len(L) -> L[i]>=0
#@ requires len(L)>0
#@ ensures forall i. 0<=i<len(L) -> result>=L[i]
m = L[0]
for k in range(len(L)):
#@ invariant forall i. 0<=i<k -> L[i]<=m
if L[k]>m:
m = L[k]
return mCette nouvelle fonction maximum est également certifiée par why3 :
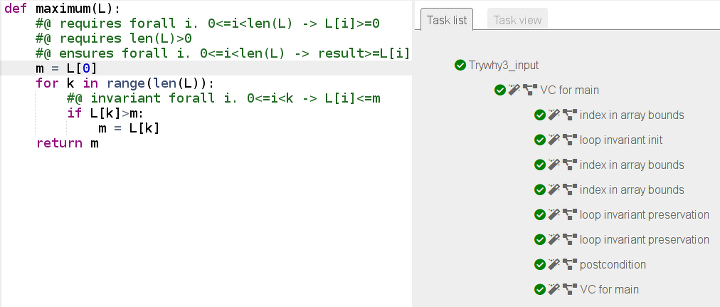
Cette nouvelle fonction maximum peut maintenant être adaptée au minimum d’une liste, simplement en échangeant les < avec des > :
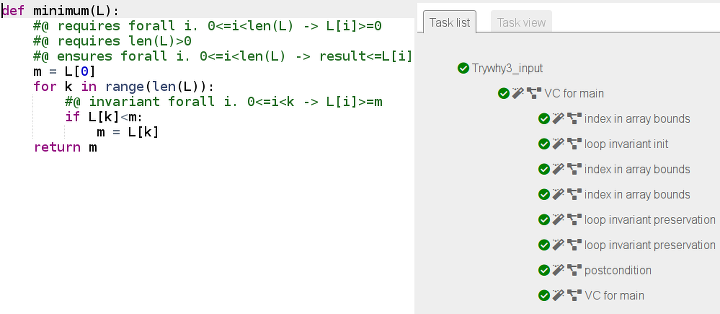
def minimum(L):
#@ requires forall i. 0<=i<len(L) -> L[i]>=0
#@ requires len(L)>0
#@ ensures forall i. 0<=i<len(L) -> result<=L[i]
m = L[0]
for k in range(len(L)):
#@ invariant forall i. 0<=i<k -> L[i]>=m
if L[k]<m:
m = L[k]
return mCette fonction minimum est certifiée par why3 :
sum
La fonction qui, à une liste (ici, d’entiers parce qu’on peut additionner des entiers), associe la somme de tous ses éléments, correspond dans le trio map-filter-reduce à un reduce, avec l’opération binaire d’addition. On convient alors que la somme d’une liste vide est égale à 0.
Ce qui donne ce script :
def somme(L):
s = 0
for i in range(len(L)):
s += L[i]
return sL’écriture est correcte du point de vue de la syntaxe :

Que prouver ?
def somme(L):
#@ ensures result==sum(L)
s = 0
for i in range(len(L)):
s += L[i]
return sLà ça ne fonctionne pas : why3 ne dispose pas de la fonction sum() de Python :

Comment aolrs prouver qu’une fonction est correcte sans utiliser la fonction ? Il faudrait pour ça récursifier la fonction, ce qui sort du programme de 1re.
Pour l’invariant aussi on a besoin de sum :
def somme(L):
#@ ensures result==sum(L)
s = 0
for i in range(len(L)):
#@ invariant s==sum([L[j] for j in range(i)])
s += L[i]
return sC’est même l’écriture d’une compréhension qui échappe à why3 :

Tout cela ne donne pas envie d’utiliser why3 pour étudier l’algorithme de sommation. Mais de toute manière
- cet algorithme est fondamentalement récursif (la somme jusqu’à n, c’est la somme jusqu’à n-1, plus le n-ième terme)
- et le programme ne cite pas la somme, mais la moyenne : on n’a même pas terminé le travail à ce stade !
Noter qu’en première technologique, en maths, l’algorithme de somme est également au programme, via la notion d’accumulateur.
Bref, il a été fait le choix de ne pas utiliser why3 pour les algorithmes de somme et de moyenne. D’ailleurs le programme précise « sur des exemples simples » et on est en droit de ne pas trouver si simple que cela ces algorithmes...
Maintenant qu’on a fini de traiter les variants et invariant « sur des exemples simples » comme le préconise le programme de 1re, on va passer aux algorithmes sur les listes : tris par insertion et sélection, recherche dichotomique dans une liste triée.
Tris
Au programme de 1re, il y a
- la preuve de correction du tri par insertion, par un invariant
- la preuve de correction du tri par sélection, par un invariant
- la preuve de terminaison de la recherche dichotomique, par un variant
Sélection
Ce script peut être certifié par la version locale de why3 :
def tri_selection(L):
#@ ensures forall i. forall j. 0<=i<j<len(L) -> L[i]<=L[j]
im = 0
for i in range(len(L)):
#@ invariant forall k. forall l. 0<=k<i<=l<len(L) -> L[k]<=L[l]
#@ invariant forall k. forall l. 0<=k<=l<i -> L[k]<=L[l]
im = i
for j in range(i+1,len(L)):
#@ invariant i<=im<j
#@ invariant forall k. i<=k<j -> L[im]<=L[k]
if L[j]<L[im]:
im = j
if im != i:
L[im], L[i] = L[i], L[im]
#@ assert forall k. 0<=k<i -> L[k]<=L[i]Mais la version en ligne utilisant l’excellent mais insuffisant Alt-Ergo ne réussit pas à valider cet algorithme.
En résumé l’invariant « le début de la liste est déjà trié » ne suffit pas, il faut également prouver que tous ses éléments sont inférieurs à tous les éléments restant à trier. On voit là un réel intérêt de why3, dont la pratique montre la nécessité de ce second invariant.
Insertion
Pour effectuer un tri par insertion en place, on décale vers la droite les éléments du tableau jusqu’à ce qu’on trouve un élément devant lequel placer celui qui était à la fin du tableau :
def tri_par_insertion(t):
#@ ensures forall i. forall j. 0<=i<j<len(t) -> t[i]<=t[j]
for i in range(1, len(t)):
#@ invariant forall k. forall l. 0<=k<l<i -> t[k]<=t[l]
j = i
while j>0 and t[j-1]>t[i]:
#@ variant j
#@ invariant 0<=j<=i
#@ invariant forall k. forall l. 0<=k<l<=i and k!=j and l!=j -> t[k]<=t[l]
#@ invariant forall k. j+1<=k<=i -> t[i]<=t[k]
t[j] = t[j-1]
j -= 1
t[j] = t[i](à vérifier avec why3)
On constate que « le début de la liste est trié » est un invariant commun aux deux algorithmes de tri au programme de 1re.
On constate également qu’il est nécessaire ici de prouver aussi la terminaison de l’algorithme. Un variant est assez facile à trouver [7]
On peut tenter aussi cette version avec échanges (plutôt que décalages) :
def tri_insertion(L):
#@ ensures forall i. forall j. 0<=i<j<len(L) -> L[i]<=L[j]
for i in range(1,len(L)):
#@ invariant forall k. forall l. 0<=k<l<i -> L[k]<=L[l]
#@ invariant forall k. forall l. 0<=k<i<=l<len(L) -> L[k]<=L[l]
j = i
while j>0 and L[j-1]>=L[j]:
#@ invariant 0<=j<=i
#@ invariant forall x. forall y. 0<=x<y<=i and y!=j -> L[x]<=L[y]
#@ variant j
L[j-1],L[j] = L[j],L[j-1]
j -= 1Dichotomie
Cet algorithme de recherche dichotomique dans une liste triée (préassertion) a été certifié par why3
def recherche(lst, x):
#@ requires forall i. forall j. 0 <= i < j < len(lst) -> lst[i] <= lst[j]
#@ ensures result <-> exists i. 0 <= i < len(lst) and lst[i] == x
inf = 0
sup = len(lst)-1
while inf <= sup:
#@ variant sup - inf
#@ invariant 0 <= inf and sup < len(lst)
#@ invariant forall i. (0 <= i < inf -> lst[i] < x)
#@ invariant forall i. (sup < i < len(lst) -> lst[i] > x)
mid = (inf + sup)//2
if lst[mid] == x:
return True
elif lst[mid] < x:
inf = mid + 1
else:
sup = mid - 1
return FalseSeule la preuve de terminaison est au programme. Cependant il est possible de formuler un invariant utilisant le fait que la liste est triée. La postcondition est que, puisque la fonction renvoie un booléen,
- ce booléen est True s’il existe un indice i tel que l’élément cherché est dans le tableau, à cet indice,
- le booléen est False si un tel indice n’existe pas (ce qui signifie que l’élément n’est pas dans le tableau)
L’invariant est qu’à tout instant l’indice auquel l’élément a des chances de se trouver est entre les bornes inférieure et supérieure, soit que
- tous les éléments du tableau qui sont avant inf sont plus petits que l’élément cherché,
- tous les éléments du tableau qui sont après sup sont supérieurs à l’élément cherché.
En ce qui concerne la partie qui est au programme, le variant le plus naturel est la longueur sup-inf de l’intervalle de recherche. On peut montrer que c’est un variant, parce qu’à chaque passage dans la boucle,
- ou bien on augmente la borne inférieure,
- ou bien on diminue la borne supérieure.
La longueur de l’intervalle est même divisée par 2 à chaque itération, ce qui rend l’algorithme très rapide.
Ainsi, l’outil why3 (version Python pour coller au programme) permet de mettre les élèves en autonomie relative : ils conjecturent un variant ou un invariant, puis le font tester par why3 avant d’appeler le professeur au secours. Ce genre d’activité, assez chronophage, présente les avantages suivants :
- L’apprentissage des élèves est actif (ils ne se bornent pas à attendre la réponse du professeur).
- On passe du temps sur les notions de variant et invariant, ce qui est nécessaire (ne serait-ce que parce que c’est au programme).
- En commençant par des exemples simples, on peut pratiquer une pédagogie par répétition dans une progression spiralaire.
- On peut même se contenter de pratiquer why3 sur des exemples simples seulement, et une fois que les notions de variant et invariant sont consolidées, aller vers un traitement moins formel de la question.
- Les élèves apprécient de manipuler des outils professionnels, qui n’ont pas été créés juste à des fins pédagogiques.
- why3 peut même être un sujet de projet...
Voir aussi
Le cours de Fred Mesnard en L3, et notamment les liens vers les tutoriels vidéo de Rustan Leino.


Commentaires