Pour commencer, une famille de pavés ayant le même volume (1 litre) et de hauteurs différentes. On affiche l’aire totale pour chercher quand elle est minimale.
Si $x$ est l’arête de la base alors l’aire de la base est $x^2$ et la hauteur est $\frac{1}{x^2}$. Alors l’aire de chaque face latérale est $x \times \frac{1}{x^2}=\frac{1}{x}$ et l’aire latérale est $\frac{4}{x}$ ; finalement l’aire totale est $2x^2+\frac{4}{x}$, fonction difficile à minimiser en seconde.
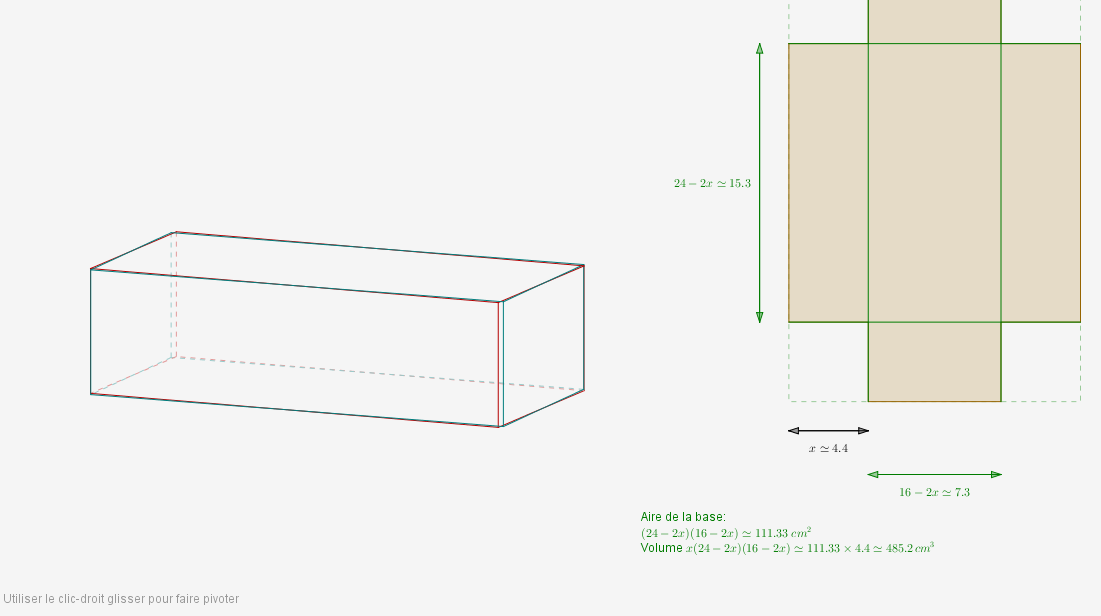
Ensuite le problème classique de la boîte sans couvercle découpée dans une feuille et dont on cherche cette fois-ci à maximiser le volume :
Les dimensions de la feuille étant supposées de 24 cm et 16 cm, et $x$ désignant la longueur découpée, la base de la boîte mesure $(24-2x)(16-2x)$ et son volume est donc $x(24-2x)(16-2x)$, fonction qui atteint son maximum lorsque $x=\frac{4\sqrt{7}+20}{3}$ : On échappe à la conjecture trop évidente...
On regarde alors le lieu des (x,x(24-2x)(16-2x) et on voit apparaître une représentation graphique et un maximum :
Les figures ci-dessus sont à rapprocher de ce diaporama où la figure tridimensionnelle n’est pas en anaglyphe (pour l’instant !) mais où le patron peut être déplié ce qui ajoute à la compréhension de la figure par les élèves.


Commentaires