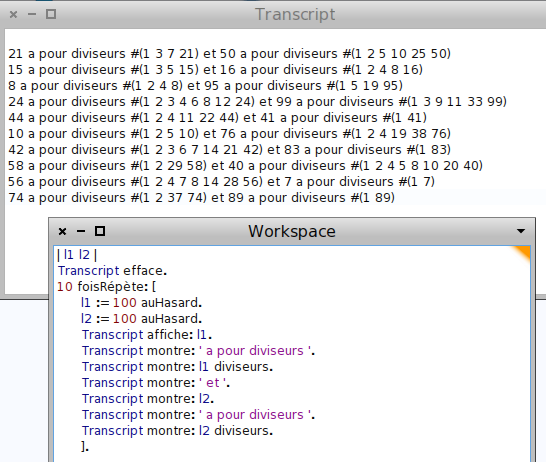
Avec MathsOntologie, il est aisé d’avoir la liste des diviseurs d’un entier [1] ; il suffit de le demander :
Transcript affiche: (2012 diviseurs).La notation « #() » est celle d’une liste, les éléments étant dans les parenthèses, séparés par des espaces. Pour savoir quel est le nombre de diviseurs de 2012, on peut donc mesurer la taille de la liste en question :
Transcript affiche: (2012 diviseurs taille).Vers des diviseurs communs
On peut alors afficher conjointement les listes de diviseurs de deux entiers choisis au hasard entre 1 et 100 :
10 répétitions portant à chaque fois sur deux nombres l1 et l2, cela fait 20 nombres, mais si le fait d’afficher deux par deux leurs listes de diviseurs fait gagner de la place, cela pose automatiquement une question : Quelle est la liste de diviseurs communs aux deux ?
On voit que pour avoir ces diviseurs communs, il suffit d’appliquer l’opération inter (notée ∩ dans le cours de maths) à ces deux listes.
Pour simplifier on peut n’afficher que les diviseurs communs :
À partir de là, il y a deux directions différentes que peut prendre l’activité :
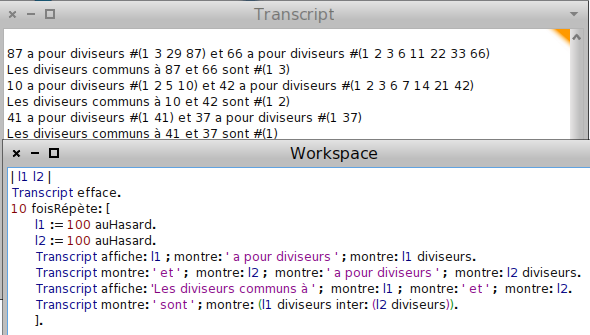
- L’examen de ces listes révèle qu’elles sont formées des diviseurs de leur plus grand élément, qu’il est alors naturel d’appeler pgcd puisque c’est exactement ce qu’il est [2]...
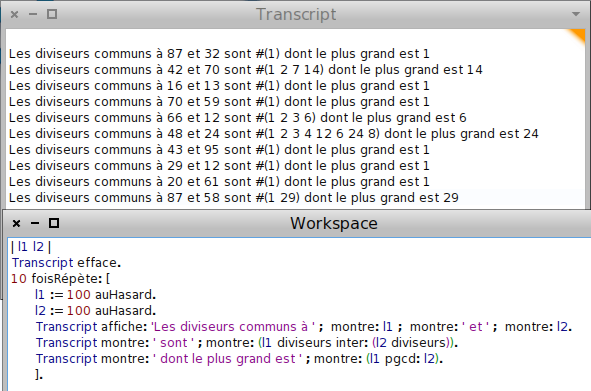
- Une constatation : La liste des diviseurs communs est souvent constituée du seul nombre 1. D’où une autre définition : Celle de nombres premiers entre eux.
La seconde direction sera traitée ci-dessous parce qu’elle mène surprenamment loin.
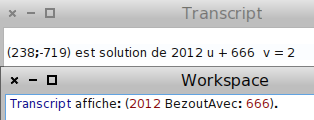
MathsOntologie possédant un test de primalité avec un autre entier, on peut directement savoir si 2012 est premier avec 666 en écrivant
Transcript affiche: (2012 estPremierAvec: 666).Avec une troisième variable appelée n et initialisée à 0, ce test permet de compter les couples de nombres premiers entre eux, en incrémentant n chaque fois que le test réussit :
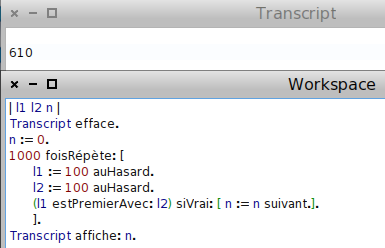
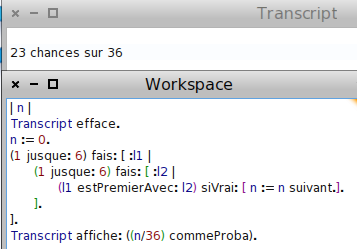
Typiquement, sur 1000 couples de nombres choisis aléatoirement entre 1 et 100, un peu plus de 600 (610 dans l’exemple ci-dessus) sont premiers entre eux.
La probabilité exacte peut être calculée par un algorithme : On parcourt tous les couples possibles dans une boucle à l’intérieur d’une autre boucle (on boucle 100 × 100 =10 000 fois), et comme ci-dessus on compte parmi ces possibilités, le nombre de couples premiers entre eux :
Exercice de troisième
On lance deux dés ; quelle est la probabilité que les résultats soient premiers entre eux ?
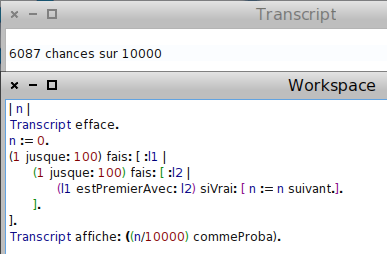
La tendance se confirme avec des nombres entre 1 et 1000 (un million de possibilités à tester) :
Or il résulte d’un théorème de Cesàro (théorie des nombres) que la probabilité en question tend vers 6/π² lorsque N est suffisamment grand (ci-dessus, N=1000) :
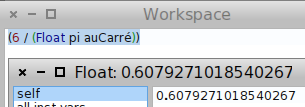
On retrouve bel et bien les 0,608 obtenus par comptage.
Aller plus loin : Bezout
Comme le pgcd de 2012 et 666 est 2, le théorème de Bachet-Bézout permet d’en déduire que l’équation 2012u+666v=2 admet une solution que l’algorithme d’Euclide étendu permet de trouver. Cette solution est donnée par MathsOntologie :
On peut vérifier que 238×2012-719×666=2...
Le manuel de MathsOntologie traite un autre exemple : L’indicatrice d’Euler, là aussi (re)découverte expérimentalement par comptage.
Commentaires