Le trio Map/Filter/Reduce se nomme en langage Snap! Map/Keep/Combine.
Pour nos élèves français, j’opterai pour Appliquer/Extraire/Combiner. Ce trio permet de manipuler des fonctions et les appliquer à une liste de données.
Le trio Map/Filter/Reduce existe dans les langages Python, Javascript, Java, et de nombreux autres langages.
Nous illustrerons dans cet exposé les exemples principalement en langage Snap!. Mais aussi en Python, langage d’excellence adopté officiellement pour coder au lycée [1].
J’attire votre attention sur le fait que les algorithmes de cet article sont évidemment perfectibles. Mon but ici n’est pas de les optimiser mais de montrer l’intérêt de Map/Filter/Reduce (ou Map/Keep/Combine) pour les coder avec les élèves.
En première lecture, je vous propose de survoler l’article du regard et d’attacher de l’importance aux images des scripts Snap! car vous risquez d’être très surpris, surtout si vous ne connaissez pas ce langage de programmation visuelle.
Vous pouvez aussi lire la table des matières détaillée avant de commencer. Vous aurez un aperçu plus complet des thèmes et exemples abordés dans cet article.
Premier tour d’horizon avec Map/Keep/Combine ou Map/Filter/Reduce
Avant d’entrer dans des détails plus techniques, je vous propose de vous laisser porter par les images des scripts fournis pour Map, Combine et Keep ci-dessous (Map/Reduce/Filter). Vous allez ainsi découvrir par vous-même à quoi servent ces trois fonctions.
Si un onglet vous paraît trop obscur au premier abord, je vous suggère de changer d’onglet, vous y reviendrez par la suite. En effet, le concept étant peut-être totalement nouveau pour vous, vous devez vous en imprégner petit à petit (à la Réunion, nous disons Ti lamp, ti lamp...).
Premiers exemples d’application de fonctions à une liste d’objets avec Map
Vous trouverez dans cette section :
- des exemples de Map pour obtenir divers tableaux de valeurs de fonctions vues au lycée,
- comment générer des listes de booléens aléatoires simplement avec Map,
- comment calculer la puissance n-ième d’une matrice sans récursivité,
- de très belles images d’un léopard pour lesquelles, grâce à Map, des modifications des codes RGB des pixels de ces images en ont délicatement changé les couleurs.
Tableau de valeurs d’une fonction
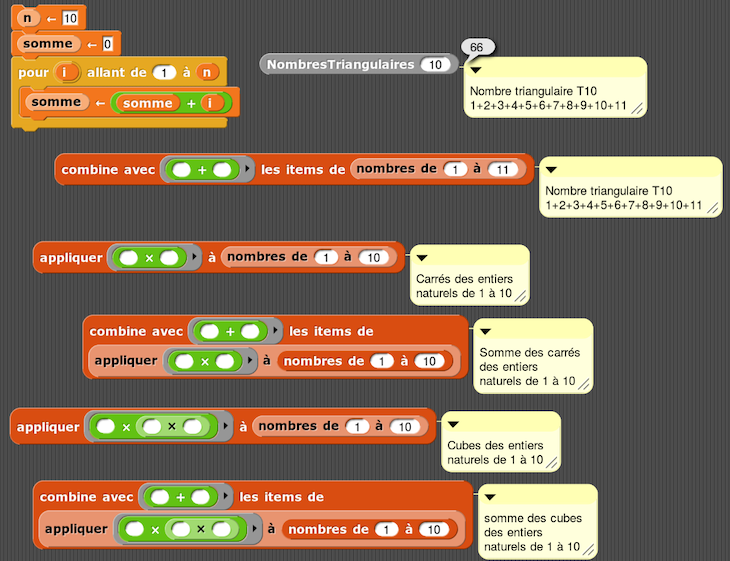
– Carrés des 7 premiers entiers

– Cubes des 7 premiers entiers

– Puissances de 10 des 7 premiers entiers

– Puissances de 2 des 7 premiers entiers

– Racine carré des 1000 premiers entiers

Le résultat obtenu donne immédiatement envie d’en extraire les nombres dont la racine est entière...
Lutin Tableaux_0 du projet Snap! lié à cet article.
— Scripts Python. [2]
def entiers_1_a_n(n): return list(range(1,n+1))
entiers_1_a_n(10)
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]def carre(x): return x**2
def carres_des_nombres(x_list):
return map(carre, x_list)
carres_des_nombres(entiers_1_a_n(10))
# renvoie [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]def cube(x): return x**3
def cubes_des_nombres(x_list):
return map(cube, x_list)
cubes_des_nombres(entiers_1_a_n(10))
# renvoie [1, 8, 27, 64, 125, 216, 343, 512, 729, 1000]def puissance_de_10(x): return 10**x
def puissances_de_10_des_nombres(x_list):
return map(puissance_de_10, x_list)
puissances_de_10_des_nombres(entiers_1_a_n(9))
# renvoie [10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000]def puissance_de_2(x): return 2**x
def puissances_de_2_des_nombres(x_list):
return map(puissance_de_2, x_list)
puissances_de_2_des_nombres(entiers_1_a_n(10))
# renvoie [2, 4, 8, 16, 32, 64, 128, 256, 512, 1024]Dans tous les scripts précédents, on aurait pu définir la fonction à mapper avec le mot-clé lambda comme dans le script suivant qui calcule les racines carrés des entiers de 1 à 1000.
map(lambda a:a**(1/2), entiers_1_a_n(1000))Retour aux onglets Premiers exemples d’application de fonctions à une liste d’objets avec Map
Obtenir une liste aléatoire de booléens
[3]
– Comment tirer au hasard un booléen Vrai ou Faux ?

– Comment créer une liste aléatoire de booléens ?
Il suffit d’appliquer le prédicat précédent à la liste des entiers de 1 à n si n est le nombre de booléens que nous souhaitons.

On pourra bien sûr en faire un bloc qui renvoie le nombre voulu de booléens :

Retour aux onglets Premiers exemples d’application de fonctions à une liste d’objets avec Map
Calcul de la puissance n-ième d’une matrice (sans récursivité)
Je suis partie de l’idée suivante.
Pour calculer $2^n$ sans utiliser d’algorithme récursif, on utilise la définition de l’élévation d’un nombre à une puissance.
J’effectue donc le produit de 2 par 2 n fois.
On va donc appliquer la fonction constante x ↦ 2 aux n premiers entiers naturels (par exemple).

Ensuite, on combine ces valeurs avec l’opérateur × .

Il en est de même pour les matrices, à condition d’utiliser pour le Combine la multiplication dans l’espace des matrices.
On se réfèrera au projet :
https://snap.berkeley.edu/snap/snap...
Voir le lutin appelé A**n .
— Scripts Python.
map(lambda a:2, entiers_1_a_n(10))
# renvoie la liste constante [2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
# on peut aussi définir fonction_constante
def fonction_constante(a_list): return map(lambda a:2, entiers_1_a_n(10))
fonction_constante(entiers_1_a_n(10))
# renvoie bien [2, 2, 2, 2, 2, 2, 2, 2, 2, 2]L’utilisation Reduce en Python nécessite d’importer la fonction reduce du module functools. [4]
from functools import reduce
reduce(lambda x,y: x * y, fonction_constante(entiers_1_a_n(10)))
# renvoie 1024 Retour aux onglets Premiers exemples d’application de fonctions à une liste d’objets avec Map
Appliquer le négatif à un rectangle de pixels colorés
Qu’est-ce qu’une image affichée sur un écran ? C’est simplement un rectangle de pixels colorés. Une image de résolution 480×360 est donc constituée de 172800 pixels, chacun ayant des attributs RGBA (Red, Green, Blue, Alpha). Si les pixels de cette image sont dans un tableau appelé screen, on peut voir les composantes des pixels choisis au hasard :
random pixel 1
(pixel beige) |
random pixel 2
(pixel marron clair) |
random pixel 3
(pixel marron clair orangé) |

Ce léopard est une image de taille 480×258.
screen est donc un tableau de 123840 pixels.

Ici, on a décidé de mettre toutes les composantes rouges de chaque pixel du léopard à 150.

On réalise cette magie à l’aide de cette fonction récursive :


Si l’on décide de passer cette image en négatif, cela nous donne un très joli effet sur le léopard (ici, il y a une erreur, c’est donc un faux négatif...).
Et voici le script pour réaliser ce faux négatif :
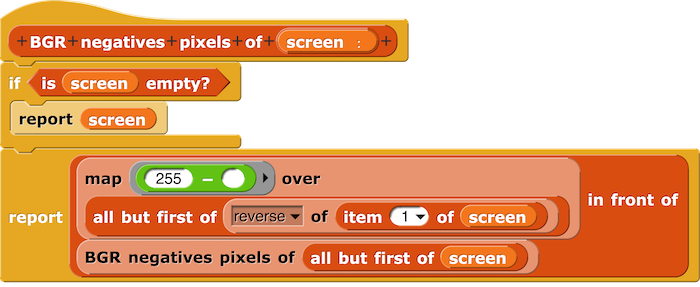

Et voici notre léopard en négatif.
Et voici le script pour réaliser ce négatif :
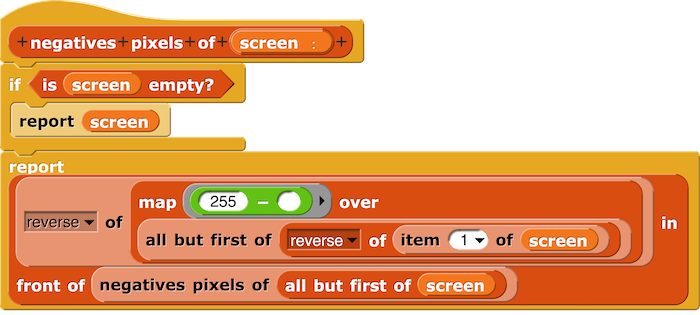
Retour aux onglets Premiers exemples d’application de fonctions à une liste d’objets avec Map
Exemples de réduction avec Combine
Pour un ensemble fini de réels, on peut lui associer son plus grand élément, sa somme, son produit, sa moyenne arithmétique, sa médiane, son nombre d’éléments… autant de fonctions qui à un ensemble de réels associent un réel unique.
Si on considère un vecteur comme un n-uplet de réels, on peut lui associer sa longueur, son produit scalaire avec un vecteur fixe, sa première coordonnée, sa norme pour une norme quelconque, l’angle qu’il fait avec un vecteur donné… [5]
Somme
– Somme des 10 premiers entiers naturels.

reduce(lambda x,y: x + y, entiers_1_a_n(10))
# renvoie la somme des 10 premiers entiers naturels, soit 55.Produit
– Produit des 10 premiers entiers naturels. [6]

reduce(lambda x,y: x * y, entiers_1_a_n(10))
# renvoie le produit des 10 premiers entiers naturels, soit 3628800.
# remarque...
from math import factorial
factorial(10) # renvoie 3628800Moyenne arithmétique
| La moyenne arithmétique de n nombres est la somme de ces nombres divisés par le nombre de nombres en jeu. |
La moyenne arithmétique des 10 premiers entiers naturels est 5,5.

– Script Moyenne arithmétique.
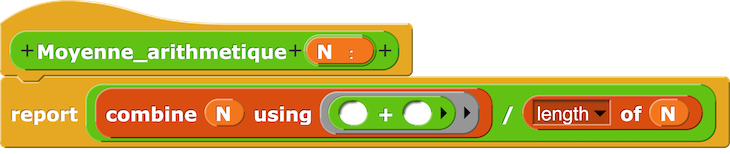
def moyenne_arithmetique(x_):
return reduce(lambda x,y: x + y, x_) / len(x_)
moyenne_arithmetique(entiers_1_a_n(10)) # renvoie 5.5Moyenne géométrique
| La moyenne géométrique de n nombres positifs est la racine n-ième du produit de ces nombres. |
La moyenne géométrique des 10 premiers entiers naturels non nuls est 4,5287 à 0,0001 près.

– Script Moyenne géométrique de nombres positifs.

def moyenne_geometrique(x_):
return reduce(lambda x,y: x * y, x_) ** (1/len(x_))
moyenne_geometrique(entiers_1_a_n(10)) # renvoie 4.528728688116765Moyenne harmonique
| La moyenne harmonique de n nombres est l’inverse de la moyenne arithmétique des inverses de ces n nombres. |
Moyenne harmonique des 10 premiers entiers naturels :

– Script Moyenne harmonique.
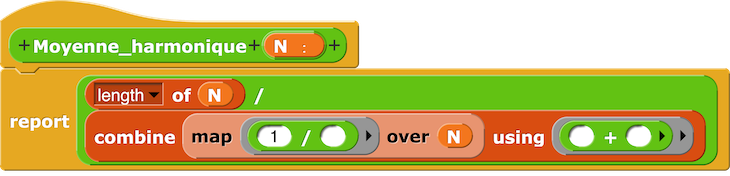
– On remarquera que la division dans Snap! peut être effectuée avec un opérateur d’ordre supérieur.

– Ce qui permet de coder encore pus simplement le script Moyenne harmonique.

def moyenne_harmonique(x_):
return len(x_) / reduce(lambda x, y: x + y, map(lambda x: 1/x, x_))
moyenne_harmonique(entiers_1_a_n(10)) # renvoie 3.414171521474055Exercice : coder la moyenne quadratique.
| La moyenne quadratique de n nombres est la racine carrée de la moyenne arithmétique des carrés de ces nombres. |
Cette moyenne est très utile en statistiques (calcul de l’écart-type) et en Théorie de la mesure.
En effet,
| L’écart type dans une population est la moyenne quadratique des distances à la moyenne. |
Produit scalaire
– Script Vecteur produit des coordonnées.
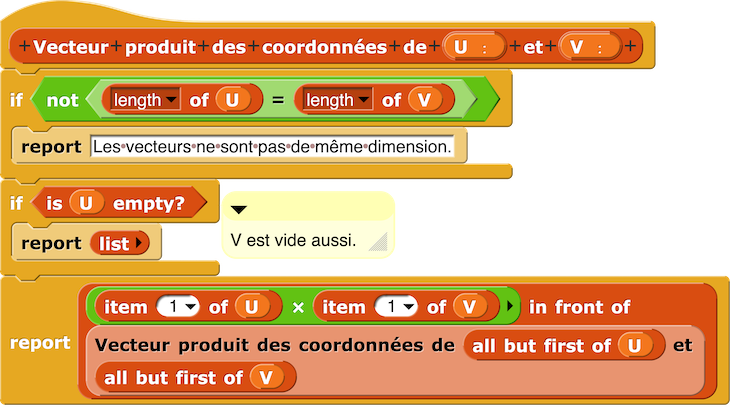
– Vecteur produit des coordonnées de 2 vecteurs de l’espace [-1, 2, 1] et [1, -2, 3].

– Script produit scalaire sans opérateur d’ordre supérieur. [7]

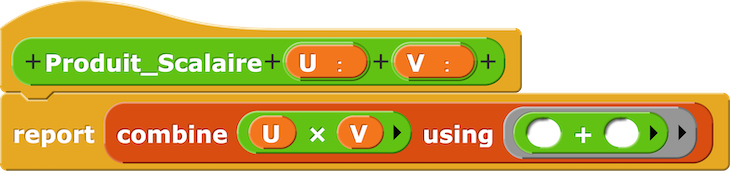
– Produit Scalaire de 2 vecteurs de l’espace.

– Le Combine du produit scalaire utilisant la multiplication comme opérateur d’ordre supérieur.

– Script produit scalaire avec opérateur d’ordre supérieur.
Voir le lutin Produit scalaire du projet Snap! lié à cet article.
Le script Python peut être le suivant, en utilisant la multiplication définie comme opérateur d’ordre supérieur. [8]
def produit_scalaire(x_, y_):
return reduce(lambda x,y: x + y, multiplier(x_, y_))
produit_scalaire([-1, 2, 1], [1, -2, 3]) # renvoie -2
produit_scalaire(entiers_1_a_n(10), entiers_1_a_n(10)) # renvoie 385Exemples d’extractions avec Keep
– Qu’est-ce qu’un prédicat ?
La fonction P : X ↦ {True, False} est appelée prédicat sur X. Lorsque P est un prédicat sur X, on dit parfois que P est une propriété de X.
Utiliser Keep (ou Filter) revient à appliquer un prédicat P à une liste de données. Ce qui permet d’obtenir une sous-liste en compréhension de la liste de données initiale. [9]
On appelle booléen l’un des éléments de l’ensemble True, False.
Voici quelques exemples de prédicats :
Ce nombre est-il positif ?
– -1 n’est évidemment pas un nombre positif...

def nombre_positif(x): return x >= 0Ce nombre est-il pair ?

def est_pair(a): return a % 2 == 0Ce nombre est-il premier ?
- 1997 est-il premier ?
 is 1997 a prime number
is 1997 a prime number
- Prédicat est-ce un nombre premier :
 Predicate is a prime number
Predicate is a prime number
Comme nous avons en Python avec Filter : [10]
filter(lambda x: 197 % x == 0, entiers_1_a_n(197)) # renvoie [1, 197]nous pouvons coder ainsi un prédicat nombre_premier en Python :
def nombre_premier(n):
return len(filter(lambda x: n % x == 0, entiers_1_a_n(n))) == 2[11]
nombre_premier(97) # renvoie Truefilter(lambda x: 197 % x == 0, entiers_1_a_n(197)) # renvoie [1, 197]Ce nombre est-il un carré ?
- 122 * 122 est un carré alors que 122 * 123 ne l’est pas :
is 122 122 a square
|
is 122 123 a square
|
- Prédicat est-ce un carré ?
 Predicate is a square
Predicate is a square
- Voici comment obtenir la liste des carrés inférieurs à 100.
 Carres inferieurs a 100
Carres inferieurs a 100
Ce code Python
49 in map(lambda x: x * x, entiers_1_a_n(round(100 ** (1/2)))) # renvoie Truepermet d’écrire le script suivant :
def est_un_carre(n): # script pour des entiers
if n < 0: return False
return n in map(lambda x: x * x, entiers_1_a_n(round(n ** (1/2))))
est_un_carre(122 * 122) # renvoie True
est_un_carre(122 * 123) # renvoie False
est_un_carre(-49) # renvoie Falsefilter(est_un_carre, entiers_1_a_n(100)). # renvoie [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]Ce nombre est-il un cube ?
- 456533 est-il un cube ?
 456533 est il un cube
456533 est il un cube
- 122 * 122 * 122 est un carré alors que 122 * 122 * 123 ne l’est pas :
is 122 122 122 a cube
|
is 122 122 123 a cube
|
- Prédicat est-ce un cube ?
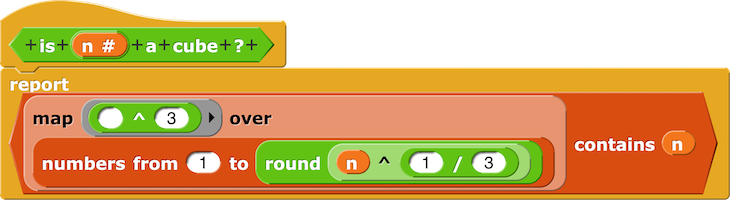 Predicate is a cube
Predicate is a cube
- Voici comment obtenir la liste des cubes inférieurs à 1000.
 Cubes inferieurs a 1000
Cubes inferieurs a 1000
def est_un_cube(n): # script pour des entiers
return n in map(lambda x: x * x, entiers_1_a_n(round(n ** (1/3))))
est_un_cube(122 * 122 * 122) # renvoie True
est_un_cube(122 * 122 * 123) # renvoie Falsefilter(est_un_cube, entiers_1_a_n(100)). # renvoie [1, 8, 27, 64]– Ce nombre est-il la somme de 3 cubes ?
- 684 est-il la somme de 3 cubes ?
 is 684 sum of 3 cubes
is 684 sum of 3 cubes684 est bien la somme de 3 cubes :
 684 comme Somme de 3 cubes
684 comme Somme de 3 cubes
- Prédicat somme de 3 cubes
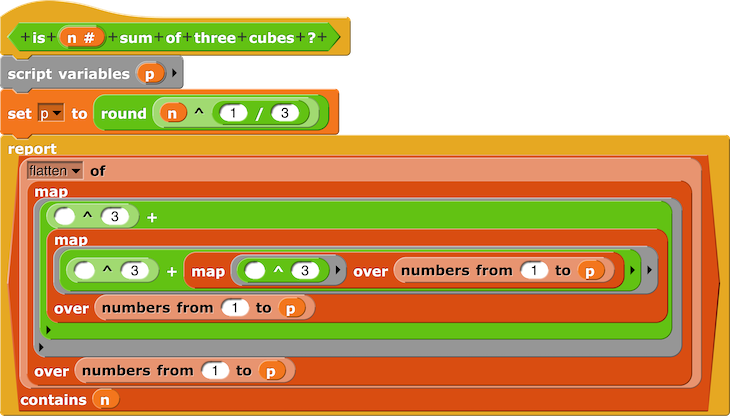 Predicate sum of 3 cubes
Predicate sum of 3 cubes
- Somme de 3 cubes inférieurs à 100 :
 Sommes de 3 cubes inferieurs a 100
Sommes de 3 cubes inferieurs a 100
– Exemples concrets d’extractions avec Keep :
Créons d’abord une liste de 10 nombres entiers aléatoires avec Map. On la nomme tyty.

Extraire les nombres positifs d’une liste de nombres
On peut extraire facilement avec Keep les items positifs de la liste tyty.

tyty = [-23,10,52,73,57,56,16,22,47,-96]
filter(est_positif, tyty) # renvoie [10, 52, 73, 57, 56, 16, 22, 47]Extraire les nombres pairs d’une liste de nombres
On peut alors extraire les nombres pairs de la liste tyty ainsi :

filter(est_pair, tyty) # renvoie [10, 52, 56, 16, 22, -96]Extraire un ensemble de carrés
On peut extraire les carrés de la liste tyty ainsi :

filter(est_un_carre, tyty). # renvoie [16]Extraire les entiers d’un ensemble de nombres
Ce test permet de savoir si un nombre est un réel ou un entier.

– Les racines entières des 50 premiers entiers s’obtiennent donc avec ce Keep en ne gardant que les nombres qui - considérés comme des chaînes de caractères - ne contiennent pas le point.

– Mais cela n’est pas très intéressant.

[12]
Nous voulons aussi garder leur antécédent... [13]
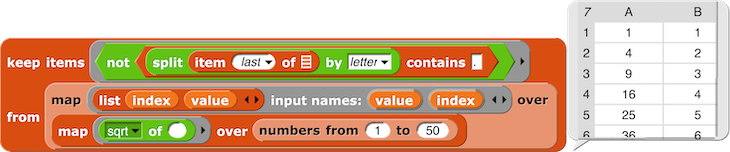
La colonne 1 du résultat comprend les nombres inférieurs à 50 dont les racines sont entières.
Lutin Tableaux_0 du projet Snap! lié à cet article.
str(5632.78)[1:3] == '.0' # renvoie False mais pour 1.0, 2.0, 3.0, etc... on obtiendrait True
c_ = map(lambda x: x ** (1/2), entiers_1_a_n(50))
filter(lambda x: len(str(x)) == 3 and str(x)[1:3] == '.0', c_)Obtenir les classes d’équivalence modulo n
Voici une note historique donnée par Alain Busser lors d’un échange autour de son jeu Union-Find :
« L’idée de modéliser les classes d’équivalences comme images réciproques par une fonction (qui caractérise la classe d’équivalence) remonte au moins à Dedekind dans sa construction des nombres. Dans son livre il définit pour la première fois le »mapping« ou image d’un ensemble par une fonction. Et ceci, avant que Cantor publie sur les ensembles ! La classe d’équivalence ne s’obtient pas par un mapping mais par un filter. »
Toute application f : E → F induit sur E la relation d’équivalence avoir même image par f.
Prenons par exemple pour un entier non nul n l’application Rₙ, Reste modulo n : m → m % n , m appartenant à ℕ.
L’ensemble des nombres qui ont même image par Rₙ sont les entiers dont la division par n fournit le même reste.
Prenons par exemple la liste Y = [2,3,1,1,9,1,1,48] qui est la liste des restes modulo 49 des nombres de cette liste :
c = [492,346,344,50,156,246,1961,587].
Le Map de la fonction f : x → Reste modulo 49(x) à la liste c = [492,346,344,50,156,246,1961,587] fournit la liste Y. [14]

On a donc : f([492,346,344,50,156,246,1961,587]) = [2,3,1,1,9,1,1,48] c’est à dire f(c) = Y.
Nous allons maintenant extraire de la liste c les items dont le reste modulo 49 est 1 avec ce Keep : [15]

L’image réciproque de 1 par f dans la liste c est donc :

Nous pouvons aussi l’écrire ainsi : [16]

Où le script de f⁻¹(valeur) dans la liste a se code de la manière suivante :

Ainsi, (Reste modulo 49)⁻¹(1) = {344,50,246,1961}, ensemble qui représente une partie de la classe d’équivalence de 1 pour la relation d’équivalence induite par l’application R₄₉.
Nous pourrons appliquer ce script à d’autres relations d’équivalence pour déterminer des parties de classes d’équivalence.
Voir le lutin index_of_item du projet Snap! lié à cet article.
Pourquoi Snap! pour coder les Mathématiques ? : Le no code - no limit langage
La diversité des articles qui ont déjà été rédigés sur le site de l’IREM de la Réunion depuis 2016 autour du langage Snap! [17] [18] et des codes qu’ils contiennent vous permettront de percevoir - si vous ne le savez pas déjà - à quel point Snap! est un langage no code - no limit...
Imaginez Scratch auquel on ajoute la puissance du lambda-calcul (λ-calcul).
L’idée de base du lambda-calcul étant que tout est fonction, vous obtenez un langage de programmation visuel (VPL) [19] qui code du code. [20]
Dans Snap!, les données sont dites de première classe.
Une donnée de type première classe peut être :
– la valeur d’une variable
– un argument d’une fonction
– la valeur de retour d’une fonction
– un membre d’une liste
– anonyme
Dans Snap!, les fonctions sont de première classe car elles peuvent constituer les entrées de n’importe quel bloc.
Une fonction qui peut prendre des fonctions comme argument ou qui renvoie une fonction est dite fonction d’ordre supérieur. Ce n’est qu’un aspect du type première classe.
Les listes y sont de première classe bien sûr. Ainsi, elles peuvent être elles-même des listes de listes.
Ce qui donne une puissance sans limite de programmation au logiciel.
C’est pour cela que Jens Mönig, principal développeur de Snap!, appelle ce langage le ´ no code - no limit language ´.
Extrait du résumé de Programming as a Medium, keynote présenté le 16 juin 2022 par Jens Mönig au APSCE CTE-STEM (International Conference on Computational Thinking Education and STEM Education) :
Snap! permet d’approcher la programmation non seulement comme un outil qui nous aide à accomplir certaines tâches comme le calcul, l’apprentissage mais aussi comme un support privilégié d’exploration. [21] [22]
Snap! est un langage de programmation visuel emprunt de la philosophie de Scratch [23]. Contrairement à Scratch, Snap! traite les blocs de code comme des citoyens de première classe au lieu de les confiner à un mode d’édition pur.
Snap! est donc exactement ce qu’il nous faut pour coder et explorer le monde des Mathématiques.
Comme vous l’imaginez bien, il n’y a pas à connaître le lambda-calcul pour coder les fonctions du lycée avec Snap!, le Scratch qui code du code... [24]
Nous nous attachons ici à ne donner que des exemples simples, qui illustrent les algorithmes clés des programmes de lycée.
La notion de Fonction au centre de l’apprentissage des Mathématiques
Dans l’article Tout est algorithme, tout est fonction, j’avais fait une première approche d’une pensée fonctionnelle du programme de première S en vigueur en 2019. J’y abordais la question fondamentale :
Qu’est-ce que la pensée algorithmique ?
C’est le fait d’analyser un problème afin de le décomposer en nombreuses petites fonctions ayant des tâches très précises, très réduites.
Dans cet article, je souhaite aller plus loin avec cette pensée fonctionnelle grâce au trio Map/Filter/Reduce, c’est à dire Map/Keep/Combine en langage Snap!.
En Mathématiques, il est courant d’appliquer une fonction à un ensemble ou à une partie d’un ensemble, et pas seulement à un élément isolé. C’est là que le trio Map/Filter/Reduce trouve tout son sens, en travaillant avec des listes d’objets qui peuvent être des nombres, mais aussi des images, des listes, des fonctions, des lutins ou un mélange de tout cela...
- La fonction Map, d’ordre supérieur, applique à chaque élément de E une fonction f:E → F.
Elle permet d’obtenir f(E), image de E par f, qui est une partie de F. [25] - La fonction Keep (Filter) envoie un ensemble E vers un sous-ensemble de E (en appliquant un test logique à chaque élément de E (un prédicat)). [26]
- Enfin, la fonction Combine (Reduce) applique un opérateur [27] à un ensemble d’objets E [28], et renvoie un objet unique. [29]
Voici comment Brian Harvey [30] décrit graphiquement de manière très explicite ce trio dans le manuel de référence du langage page 50.

La puissance des listes conjuguée à une pensée fonctionnelle
Aborder un algorithme à l’aide de listes et l’application exclusive du trio Map/Keep/Combine va donner une dimension supérieure à l’application de cet algorithme. Voici comment Mathematica décrit l’utilisation qu’il fait des listes :
« Lists are central constructs in the Wolfram Language, used to represent collections, arrays, sets, and sequences of all kinds. Lists can have any structure and size and can routinely involve even millions of elements. Well over a thousand built-in functions throughout the Wolfram Language operate directly on lists, making lists a powerful vehicle for interoperability. »
C’est cette vision des listes qui donne à Mathematica une telle puissance pour la résolution des algorithmes. Le langage Snap! a également été écrit dans cette optique : celle de permettre une programmation fonctionnelle en travaillant délibérément sur des objets de première classe, en particulier, des fonctions d’ordre supérieur et des listes de listes...
Nous voulons ici montrer à l’aide de nombreux exemples que nous pouvons nous aussi coder les algorithmes grâce à une pensée fonctionnelle exclusive, et que cela est abordable par nos élèves.
De la décomposition canonique d’une application à une décomposition de type Map/Filter/Reduce
La décomposition canonique d’une fonction se fait naturellement comme étant la composée : s o b o i .
(s = surjection, b = bijection, i = injection) [31]
Ce principe n’est pas utilisable mais donne sujet à réflexion. Au vu de tous les exemples que nous avons pu étudier, il semblerait que toute fonction calculable [32] puisse s’obtenir à l’aide de la composée de fonctions choisies parmi { Map , Filter, Reduce }, dans n’importe quel ordre, à condition d’autoriser des appels récursifs à ces fonctions. [33]
D’après la thèse de Alonzo Church concernant la définition de la notion de calculabilité,
Toutes les applications calculables peuvent être calculées en utilisant des fonctions récursives.
Par ailleurs, nous avons remarqué, au fil des exemples rencontrés depuis plusieurs mois, qu’un grand échantillon des applications calculables peut être implémenté à l’aide de fonctions d’ordre supérieur (bien sûr en autorisant des appels récursifs), notamment du type Map/Filter/Reduce.
Nous aimerions bien que cela nous conduise à cette affirmation...
Un grand nombre de fonctions calculables peut s'évaluer par un algorithme du type Map/Filter/Reduce.
Au lieu de fonder les mathématiques sur la notion d’ensemble, on peut fonder les mathématiques autour de la notion de fonction. On pourra commencer à ce sujet par lire cet article de Pierre Lescanne : Et si on commençait par les fonctions !.
De nombreux sites proposent des explications plus ou moins simples de ce qu’est le lambda-calcul et la programmation fonctionnelle, mais ne cherchez pas trop simple ; de toute façon, c’est compliqué ;-) ! Personnellement, je me cantonne au codage de fonctions mathématiques avec l’usage exclusif de fonctions, et vous verrez, au fur et à mesure, on entre petit à petit dans l’esprit de la programmation fonctionnelle.
Par exemple, pour rester en mode fonctionnel, on évitera d’utiliser for each item pour parcourir une liste. Brian Harvey explique cela très bien dans le paragraphe Functional and Imperative List Programming page 48 du manuel de référence de Snap! 7.0. [34]
Écrire un algorithme, c'est décomposer le problème en une suite de fonctions aussi simples que possible.
d’après Jeannette Wing
Écrire un algorithme, ce sera donc écrire une série de fonctions permettant de résoudre cet algorithme, sachant qu’une fonction est obtenue grâce à un enchainement des opérateurs de référence : + , × .
Exemples progressifs niveau lycée
Vous trouverez dans cette section comment coder avec map des tableaux de valeurs pour une fonction du second degré avec des pas différents, le codage des coefficients binomiaux k parmi n avec deux combine, celui de la somme des k parmi n, un onglet de statistiques dans lequel nous adoptons le point de vue de John Tukey selon lequel une série statistique est résumée par les cinq valeurs caractéristiques : minimum, 1er quartile, médiane, 3e quartile, maximum.
La recherche du minimum ou du maximum d’une liste représentant un tableau de valeurs se fera en utilisant Combine et l’opérateur a min b ou a max b .
Second degré
On peut coder une fonction du second degré x ↦ a x² + b x + c ainsi :

[35] L’image de 100 par la fonction du second degré x ↦ 2 x² - 3 x + 1 est 19701.

On peut mapper cette fonction
– sur les entiers de l’intervalle [-3, 4] afin d’obtenir, par exemple, un tableau de valeurs de cette fonction pour les entiers de cet intervalle :

– sur la subdivision réelle par pas de 0.1 des nombres entiers de l’intervalle [0, 6].

Mais si dans le script précédent, on entre une liste comme argument [36], on obtient le script suivant :

Ce qui nous permet d’obtenir un tableau de valeurs simplement en appelant le script précédent :

On peut même obtenir un pas sur l’intervalle de départ :

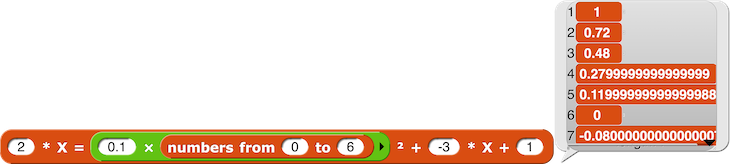
Voir le lutin Second degré du projet Snap! lié à cet article.
Combinaisons de k éléments d’un ensemble à n éléments
– k parmi n s’obtient en faisant la division de 2 Combine.
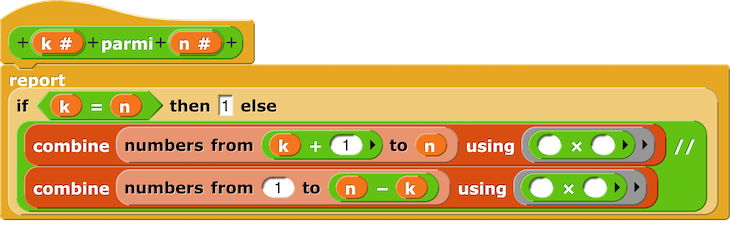
Il y a 210 parties à 4 éléments dans un ensemble à 10 éléments.

– Coefficients binomiaux k parmi 5, k allant de 0 à 5.

– Le triangle de Pascal s’obtient avec deux Map imbriqués.
Somme des (k parmi n) = 2ⁿ
– Somme des k parmi 5, k allant de 0 à 5. [37]

– Somme des k parmi 10, k allant de 0 à 10. [38]

Voir le lutin Combine du projet Snap! lié à cet article.
Maximum, minimum, quartiles, médiane
Le maximum, le minimum, les premier et troisième quartiles q1 et q3, la médiane sont les 5 valeurs caractéristiques d’une série statistique au sens de John Tukey. Il appelle ces cinq valeurs Résumé à 5 valeurs d’une série statistisque. Ce résumé à 5 valeurs est une façon de transmettre l’information essentielle dans une distribution. [39]

Script maximum de deux nombres
Script maximum de deux nombres |

Script minimum de deux nombres
Script minimum de deux nombres |
Soit alpha_0 = [5, 9, 7, 10, 4, 3, 6, 10, 1, 2] une série de 10 données que nous prenons pour illustrer nos calculs.
Nous devons d’abord l’ordonner : alpha = [1, 2, 3, 4, 5, 6, 7, 9, 10, 10]
Ainsi, le maximum de la série de données alpha s’obtient avec ce Combine : [40]

Et son minimum :

| La médiane d’une série statistique partage l’ensemble ordonné de ses observations en deux parties égales. |
Par exemple, la médiane de la liste des 33 premiers nombres de Carmichael [41] est 101101, elle s’obtient avec ce Keep :

Nous devons distinguer les séries ayant un nombre de données impair de celles ayant un nombre de données pair.
D’où le script médiane d’une série de données alpha : [42]
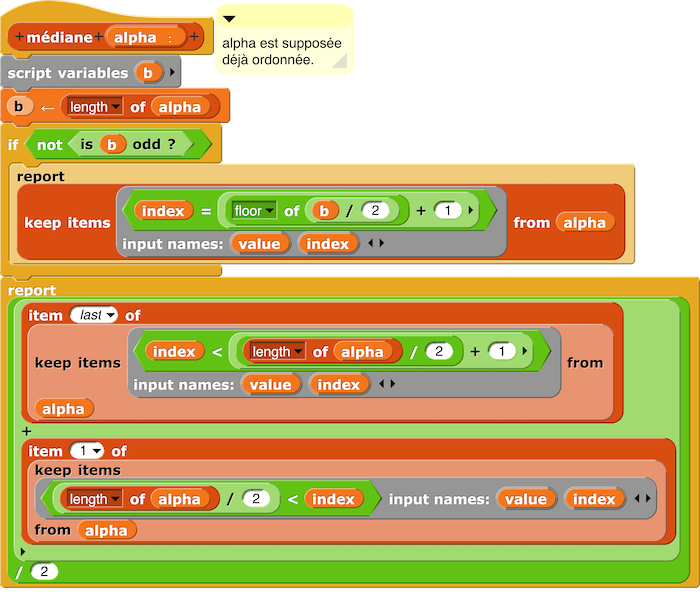
– Script rang de la médiane d’une série de données alpha [43]

La médiane de alpha est 5,5. Son rang est 5,5.
| Les quartiles q1, q2 (la médiane), et q3 d’une série statistique partagent un ensemble ordonné d’observations en quatre parties égales. |
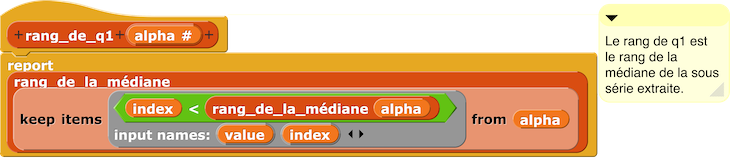
– Script premier quartile q1 d’une série de données alpha : q1 est la médiane de la 1re sous-série extraite lorsque l’on scinde la série de départ en deux séries de longueurs égales.

– Script rang de q1 d’une série de données alpha
– Script troisième quartile q3 d’une série de données alpha : q3 est la médiane de la 2nde sous-série extraite lorsque l’on scinde la série de départ en deux séries de longueurs égales.
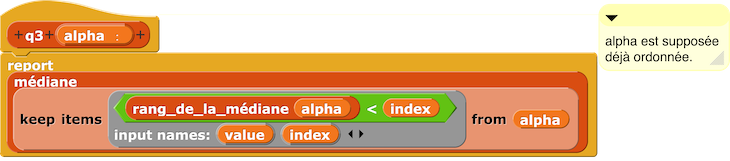
– Script rang de q3 d’une série de données alpha

Enfin, nous pouvons obtenir le résumé de la série statistique alpha au sens de John Tukey.
– Script 5 valeurs caractéristiques de la série statistique alpha au sens de John Tukey

Les 5 valeurs caractéristiques de la série statistique alpha au sens de John Tukey sont :
[min, q1, med, q3, max] = [1, 3, 5.5, 9, 10]
– Script informations statistiques sur alpha

D’où les premières informations statistiques de la série alpha :
et celle des 33 premiers nombres de Carmichael :
Exercices
En vous inspirant des exemples précédents, on pourra :
– Coder les premier et neuvième déciles d1 et d9 [44].
– Extraire les nombres de la série dans l’intervalle interquartile [q1, q3] et les nombres de la série dans l’intervalle interdéciles [d1, d9].
– Écrire un script qui ayant entré une liste de données, renvoie une liste qui représente en mode texte le diagramme stem-and-leaf d’une distribution. Ce diagramme est une forme de graphique de fréquences. Ce diagramme est très intéressant à coder, car, contrairement aux histogrammes, il garde les informations concernant les données, et peut même s’appliquer à des données non numériques.
La série de données [20, 30, 32, 35, 41, 41, 43, 47, 48, 51, 53, 53, 54, 56, 57, 58, 58, 59, 60, 62, 64, 65, 65, 69, 71, 74, 77, 88 and 102] sera repésentée ainsi avec un diagramme stem-and-leaf :
2 | 0
3 | 025
4 | 11378
5 | 133467889
6 | 024559
7 | 147
8 | 8
9 |
10 | 2
On classe d’abord les données par ordre de grandeur [45]. On choisit ensuite le stem, ici on prend les dizaines. Les leaves sont les unités.
Voir le lutin John_Tukey du projet Snap! lié à cet article.
ToDo list
En statistiques, on pourra s’amuser à coder l’espérance, la variance, et l’écart-type d’une série de données.
Un peu d’arithmétique
L’arithmétique est un domaine des Mathématiques qui se prête particulièrement au codage avec des listes. Il est même presque intuitif de coder les problèmes d’arithmétique avec le trio Map/Keep/Combine (Map/Filter/Reduce).
Le lutin Nb_Premiers du projet Snap! lié à cet article est consacré à l’arithmétique. On y trouvera tous les scripts proposés ci-dessous.
Diviseurs de n
– Liste des diviseurs de n
Prenons par exemple le nombre 323. 323 est le produit 17 × 19 ainsi 323 possède 4 diviseurs : 1, 17, 19 et 323.
Le prédicat Reste nul pour 323 mod n, n <= 323 renvoie donc 4 True sur 323 booléens.

On garde alors les items True du prédicat Reste nul pour 323 mod n

Ceci nous donne le script Liste des diviseurs de n. [46]
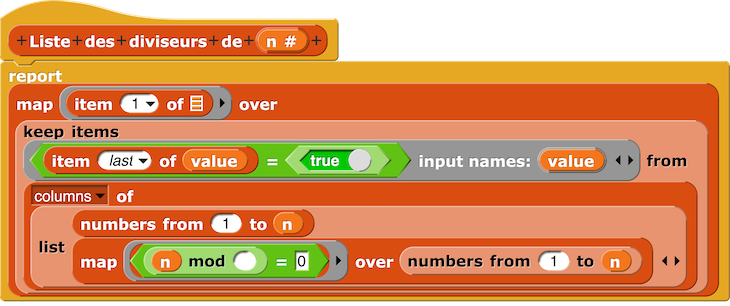
Liste des diviseurs de 100. [47]
Liste des diviseurs de 100
|
Liste des diviseurs de 101. 
Liste des diviseurs de 101
|
Liste des diviseurs de 323. 
Liste des diviseurs de 323
|
Liste des diviseurs de 997. 
Liste des diviseurs de 997
|
Liste des diviseurs de 998. 
Liste des diviseurs de 998
|
Liste des diviseurs de 1001. [48] 
Liste des diviseurs de 1001
|
– Nombre de diviseurs de n

323 possède 4 diviseurs 1, 17, 19 et 323.

– Somme des diviseurs de n

La somme des diviseurs de 100 est 217.
En effet, 1 + 2 + 4 + 5 + 10 + 20 + 25 + 50 + 100 = 217
Nombres premiers
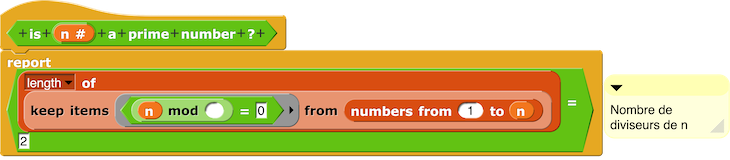
Le nombre de diviseurs de 323 s’obtient en demandant la longueur de ce Keep :

Et n est premier si son nombre de diviseurs est égal à 2.
D’où le script is n a prime number ?.


101107 est premier. 101107 sur le site NumberEmpire.
– Crible d’Ératosthène
Script Help Crible d’Ératosthène

Help Crible d’Ératosthène


Script Crible d Eratosthene
Script Crible d’Ératosthène |
Crible d’Ératosthène appliqué a 100. 
Crible d Eratosthene applique a 100
|
On retrouvera grâce au crible d’Ératosthène qu’il y a 25 nombres premiers inférieurs à 100 : [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
Et 168 nombres premiers inférieurs à 1000 :
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,
139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,
281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,
443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,
613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,
787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,
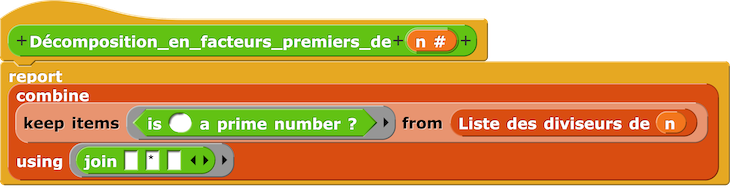
971,977,983,991,997]– Décomposition en facteurs premiers
Décomposition en facteurs premiers de 561.

Script Décomposition en facteurs premiers
Fonction Phi d’Euler
Définition de la fonction phi d’Euler :
| Pour tour entier n >= 1, φ(n) est le nombre d’entiers compris entre 1 et n (inclus) qui sont premiers avec n. |
– Script Nombres premiers avec n inférieurs à n.


On vérifiera grâce à ce script qu’il y a 40 nombres premiers avec 100 inférieurs à 100. Ainsi, φ (100) = 40. [1,3,7,9,11,13,17,19,21,23,27,29,31,33,37,39,41,43,47,49,51,53,57,59,61,63,67,69,71,73,77,79,81,83,87,89,91,93,97,99]
Et 400 nombres premiers inférieurs à 1000. Ainsi, φ (1000) = 400.
– Script Fonction Phi d’Euler.


Fonction Phi d’Euler appliquée à 100.

Fonction Phi d’Euler appliquée à 81.
Test de primalité de Fermat
Le petit théorème de Fermat s’énonce comme suit :
| si p est un nombre premier et si a est un entier quelconque, alors a^p – a est un multiple de p |
Le Map de la fonction x → x ^ 113 modulo 113 renvoie les index de chaque item, car 113 est premier (d’après le petit théorème de Fermat).
Nous avons besoin pour ce test d’activer
Use BigNumbers de la librairie Bignums, rational, complex

Script Petit théorème de Fermat.

Petit théorème de Fermat appliqué à 113.

Script Test de primalité de Fermat.
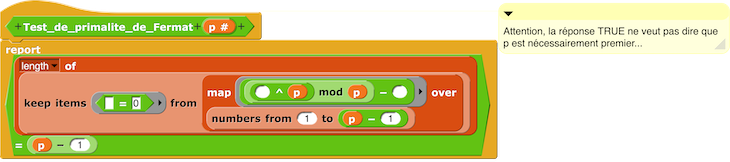

Le test de primalité de Fermat appliqué à 113 répond naturellement True,

tandis que le test de primalité de Fermat appliqué à 112 répond naturellement False.
Le test de primalité de Fermat appliqué à 561 donne comme réponse True pourtant,

la liste des diviseurs de 561 est :
Donc 561 = 3 x 11 x 17.
561 est un nombre de Carmichael pour lesquels le test de primalité de Fermat donne True.
On pourra consulter THE ON-LINE ENCYCLOPEDIA OF INTEGERS SEQUENCES.
Ainsi, les 33 premiers nombres de Carmichael sont listés sur cette page.
ToDo list
– Recherche de nombres premiers particuliers (Mersenne, Fermat)
33 premiers nombres de Mersenne notés Mₙ :
[0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575, 2097151, 4194303, 8388607, 16777215, 33554431, 67108863, 134217727, 268435455, 536870911, 1073741823, 2147483647, 4294967295, 8589934591]
On se demande quels sont les nombres de Mersenne premiers.
« Il existe un test de primalité efficace pour les nombres de Mersenne, le test de primalité de Lucas-Lehmer ; de ce fait, les plus grands nombres premiers connus sont des nombres de Mersenne. Les nombres de Mersenne premiers sont pourtant rares : seulement 51 sont connus début 2022. On ne sait même pas s’il en existe une infinité. » [49]
Test de primalité de Lucas-Lehmer
Édouard Lucas a développé ce test le premier dans sa Théorie des fonctions numériques simplement périodiques en 1878.

Test de primalité de Lucas-Lehmer pour les nombres de Mersenne
Je vous propose d’appliquer le théorème énoncé dans ce test de primalité pour écrire un script qui détermine si un nombre de Mersenne Mₙ est premier. [50]
– Détermination de triplets pythagoriciens
Ce sont les triplets de la forme $ x² + y² = z² $. [51]
– Somme de 2 carrés, somme de 3 carrés, somme de 4 carrés
Lagrange a démontré en 1770 que tout nombre entier est somme de 4 carrés.
Écrire un script qui pour un entier n renvoie une liste [p, q, r, s] telle que $n = p² + q² + r² + s²$ .
– Somme de 2 cubes
J’adore cette anecdote à propos de Srinivasa Ramanujan rapportée par le mathématicien Godfrey Harold Hardy. Hardy parlant du numéro d’immatriculation sans intérêt du taxi qu’il venait de prendre, Ramanujan lui rétorque que ce numéro est au contraire très intéressant :
« 1729 est le plus petit nombre décomposable en somme de deux cubes de deux manières différentes. » [52]
Écrire un script qui renvoie pour un entier n les sommes de 2 cubes non dupliquées inférieures à n sous la forme $x³ + y³$ [53].
– Algorithme d’Euclide-Bézout
Écrire un script pour l’algorithme Bézout-Blankinship récursif.
Calculs sur les suites
L’utilisation du trio Map/Filter/Reduce est particulièrement intéressant pour les calculs sur les suites.
Somme des termes d’une suite
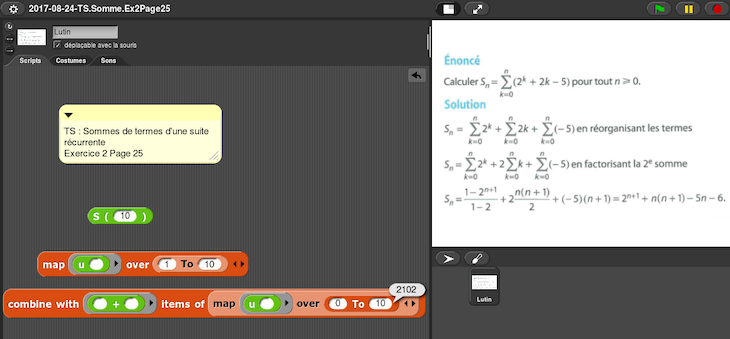
J’ai expérimenté en classe le codage des suites numériques avec Map/Combine en première S pendant l’année scolaire 2018-2019 [54].
– Voir ce premier exemple
– Somme des termes d’une suite arithmétique
– En Terminale S (année scolaire 2017-2018)
[55]
Voir le lutin Suites SA et SG du projet Snap! lié à cet article.
Produit des termes d’une suite
– Le produit des premiers entiers naturels inférieurs à n nous donne n!.
Ainsi 10! = 1 x 2 x 3 x ... x 10 = 3628800

On aura donc le choix pour coder la fonction factorielle entre ces deux scripts :


Voir le lutin Combine du projet Snap! lié à cet article.
Suite de Fibonacci
La suite des nombres de Fibonacci commence ainsi [1,1,2,3,5,8,13,..], dans laquelle, hormis les deux premiers termes 1 et 1 qui servent à initialiser la suite, les termes sont obtenus comme somme des deux précédents.
Ainsi, le 12-ième nombre de Fibonacci est 144.

On peut coder le calcul du n-ième nombre de Fibonacci à l’aide de ce script récursif :

Ce qui nous permet d’écrire ce script qui renvoie du 1er au n-ième nombre de Fibonacci :

Map du 1er au 5-ième nombre de Fibonacci :

On peut aussi construire autrement la liste des premiers nombres de Fibonacci :
– Script Help nombres de Fibonacci jusqu’au n-ième

– d’où le Script Nombres de Fibonacci jusqu’au n-ième


Avec lequel nous obtenons :
Voir le lutin Fibonacci du projet Snap! lié à cet article.
Suite de Syracuse
Voici la définition de la suite de Syracuse donnée dans Wikipedia :
| On appelle suite de Syracuse une suite d’entiers naturels définie de la manière suivante : on part d’un nombre entier strictement positif ; s’il est pair, on le divise par 2 ; s’il est impair, on le multiplie par 3 et l’on ajoute 1. |
Script suite de Syracuse pour u₀ appliquée à n :
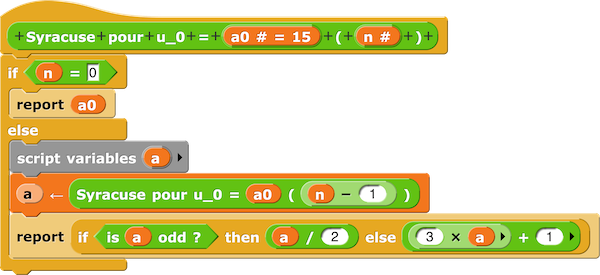
Script Syracuse pour u0 egale 12 applique a 100
|
Script Syracuse pour u0 egale 15 applique a 20
|
Script suite de Syracuse du nombre a₀ jusqu’au rang n


Exemple avec u₀ = 15 jusqu’au rang 18 :
Map de la suite de Syracuse pour u₀ = 10 sur les entiers de 0 à 7 :

Suite de Syracuse de 77671 jusqu’au rang 260 nous fournit la résultat suivant :
On pourra le vérifier à l’aide de ce lien.
| La conjecture de Syracuse [56], ou conjecture de Collatz, affirme que pour tout entier N > 0, il existe un indice n tel que uₙ = 1. |
Il existe tout un vocabulaire autour de cette suite :
– Temps de vol : c’est le plus petit indice n tel que uₙ = 1.
L’index du 1er item de la liste des termes de la suite de Syracuse pour u₀ = 77671 est 232.

Ce qui nous fournit le script Temps de vol suite de Syracuse suivant :
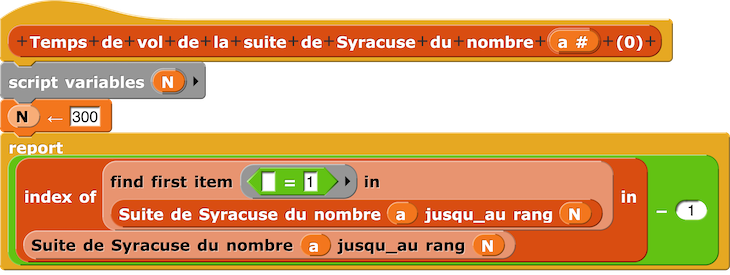
Ainsi, le temps de vol de la suite de Syracuse pour u₀ = 77671 est 231.


Le Map de la fonction liste(index, value) sur la suite de Syracuse du nombre 15 jusqu’au rang 18 fournit :
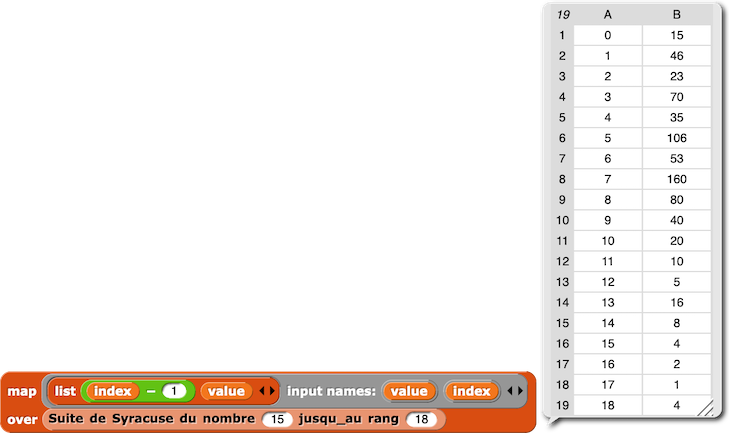
Le 1er item égal à 1 dans la liste des termes de la suite de Syracuse du nombre 15 jusqu’au rang 18 s’obtient avec ce bloc :

L’index du 1er item égal à 1 dans la liste des termes de la suite de Syracuse du nombre 15 jusqu’au rang 18 s’obtient donc ainsi :

Ce qui nous fournit le script Temps de vol suite de Syracuse plus efficace que le précédent [57] :


dans lequel le script Help est :
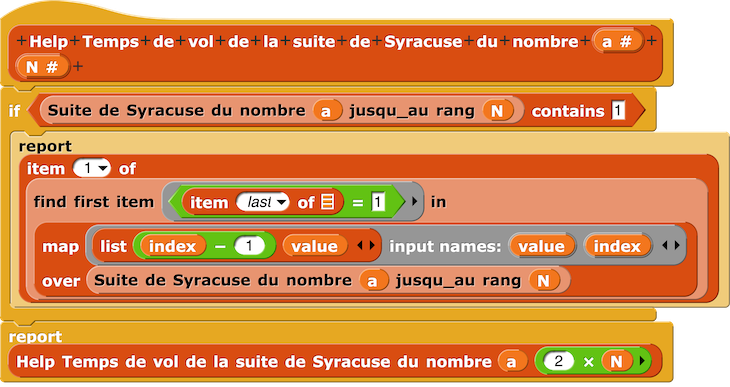
Le temps de vol de la suite de Syracuse pour u₀ = 15 est 17.

– Temps de vol en altitude : c’est le plus petit indice n tel que uₙ₊₁ < u₀.
Script Temps de vol en altitude suite de Syracuse [58]


dans lequel le script Help est :
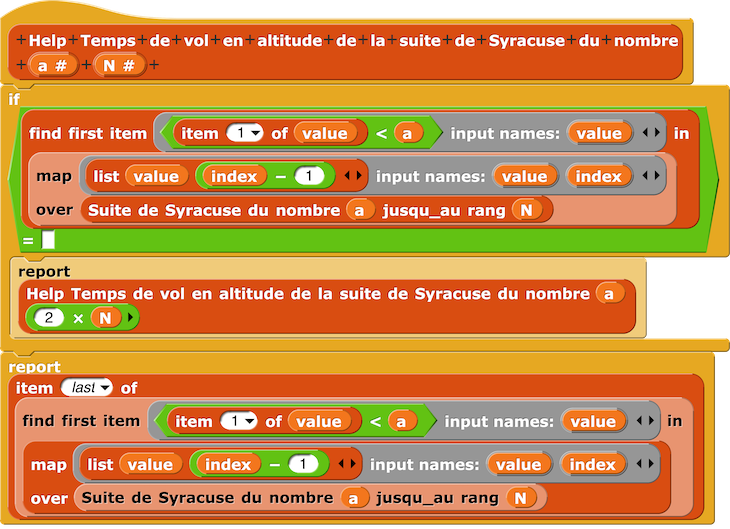
Le temps de vol en altitude de la suite de Syracuse pour u₀ = 15 est 11.

– Altitude maximale : c’est la valeur maximale de la suite.
Le maximum de la suite de Syracuse du nombre 77671 s’obtient grâce à un Combine.

Ainsi, l’altitude de la suite de Syracuse du nombre 77671 est de 1570824736 (et son temps de vol est 231).
On sait qu’une fois 1 atteint, le maximum a déjà été atteint. D’où le script Altitude maximale de vol de la suite de Syracuse pour u0 donné :
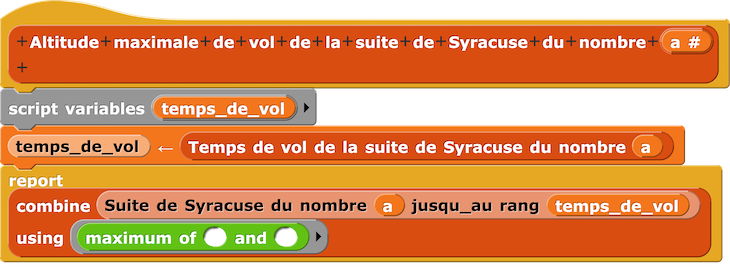
- Altitude maximale de la suite de Syracuse du nombre 127 :
 Altitude maximale suite de Syracuse du nombre 127
Altitude maximale suite de Syracuse du nombre 127 - Altitude maximale de la suite de Syracuse du nombre 15 :
 Altitude maximale suite de Syracuse du nombre 15
Altitude maximale suite de Syracuse du nombre 15 - Altitude maximale de la suite de Syracuse du nombre 14 :
 Altitude maximale suite de Syracuse du nombre 14
Altitude maximale suite de Syracuse du nombre 14 - Altitude maximale de la suite de Syracuse du nombre 121 :
 Altitude maximale suite de Syracuse du nombre 121
Altitude maximale suite de Syracuse du nombre 121
Voir le lutin Syracuse du projet Snap! lié à cet article.
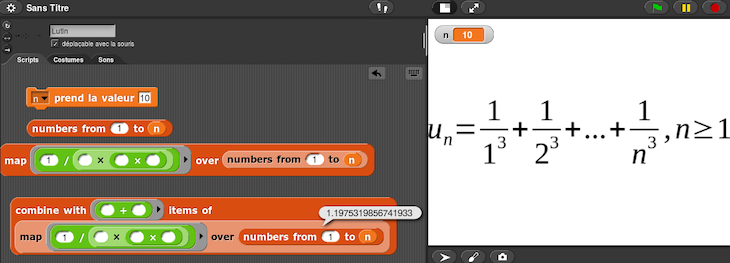
Suite ((1 + 1/n )ⁿ)
Voici les 5 premiers termes de la suite (1 + 1/n)ⁿ :

Cette suite tend vers le nombre d’Euler lorsque n croît, mais elle est à convergence très lente.

On voit en effet qu’il faut attendre n = 1 000 000 pour avoir les 5 premiers chiffres exacts de e.

e = 2.71828182845904523536028747135266249775724709369995... [59]
Voir le lutin e = lim((1+1/n)ⁿ) du projet Snap! lié à cet article.
On pourra aussi consulter le lutin e qui fournit une comparaison de 3 méthodes d’approximation de e. Voir l’onglet Encadrement de e dans les recherches de valeurs approchées de nombres réels.
Applications : Recherche de valeurs approchées
On pourra effectuer des recherches de valeurs approchées de π, e, √2 , φ = (1 + √5)/2 , ln(2), etc... grâce à des algorithmes bien choisis.
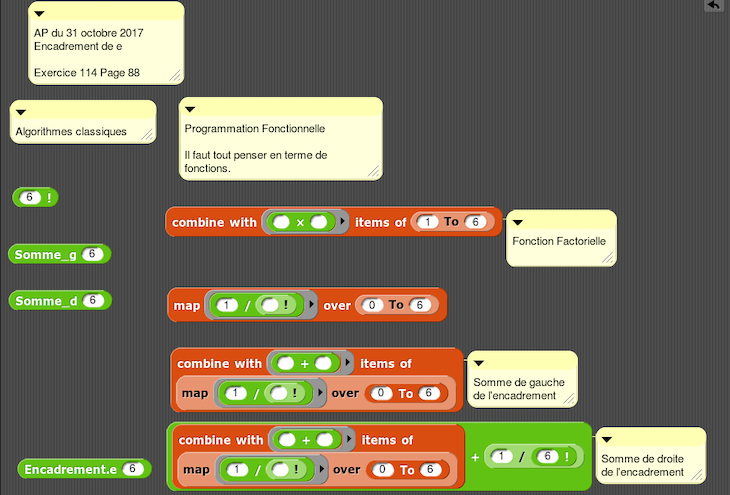
Encadrement de e
1. Encadrement de e par programmation fonctionnelle en Terminale S (année scolaire 2017-2018).
2. On pourra comparer trois méthodes pour approcher le nombre d’Euler et tester leur efficacité dans le lutin e qui fournit une comparaison de ces 3 méthodes d’approximation de e.
- Méthode 1
| Définition de e par Euler comme somme de la série Σ(1/n !) (de n = 0 à +∞) |


- Méthode 2
| La suite numérique de terme général ((1 + 1/n)ⁿ) tend vers e lorsque n tend vers +∞ |
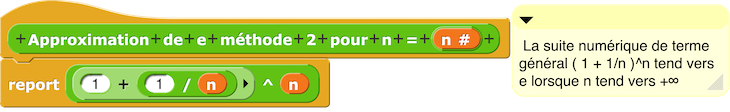

- Méthode 3
Cet élégant algorithme nous vient d’un tweet dans lequel le théorème suivant est cité :
| La racine n-ième de la moyenne géométrique des coefficients binomiaux de la n-ième ligne du triangle de Pascal tend vers √e lorsque n tend vers +∞. |
Malheureusement, il se révèle être inefficace pour l’approximation de e.


Ce Map permettra d’embrasser les 3 méthodes d’un seul clic :

Approximation de π par Ramanujan
L’une des formules fournissant une approximation de π à convergence rapide a été trouvée par le mathématicien indien Srinivasa Ramanujan en 1910.
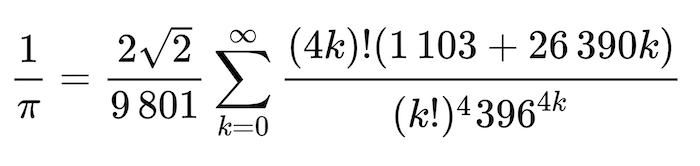
Valeurs approchées de Pi par Ramanujan : la fonction à sommer

Script Valeurs approchées de Pi
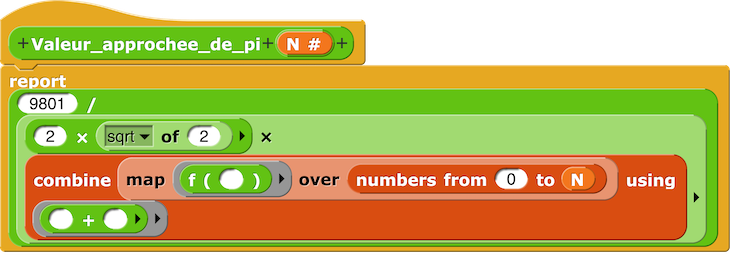
Il faut bien sûr activer la librairie BigNumbers.
Valeurs approchees de Pi 0
|
Valeurs approchees de Pi 1
|
Valeurs approchees de Pi 5
|
Valeurs approchees de Pi 10
|
On pourra mapper Valeurs approchées de Pi de 0 à 50. [60]

ToDo List
– Suites adjacentes tendant vers le nombre d’Or φ = (1 + √5)/2
– Suites tendant vers √2
– Suites tendant vers ln(2)
Et en géométrie ?
Cette partie est visible sur le site de la revue Sesamath MathemaTICE : http://revue.sesamath.net/spip.php?... .
De l’intérêt du Map/Keep/Combine
Travail sur les listes
Cette section développe la pertinence de travailler sur des listes de nombres.
– Comment obtenir tous les index d’un item dans une liste,
– Comment renverser une liste,
– Comment insérer un élément dans une liste,
– Un algorithme pour shuffle (secouer les éléments d’une liste).
Voir le lutin Listes du projet Snap! lié à cet article.
Tous les index d’un item dans une liste
Reprenons notre liste Y = [2,3,1,1,9,1,1,48] qui est la liste des restes modulo 49 des nombres de la liste c dans l’onglet Obtenir les classes d’équivalence modulo n des exemples d’extraction avec Keep.
Cherchons les index de 1 dans la liste Y. Ce seront aussi les index des antécédents de 1 dans la liste c par la fonction f.
Les index d’un item dans une liste sont ni plus ni moins les antécédents de cet item par la fonction Liste.
|
|

On mappe la fonction Liste(valeur, index) pour obtenir la liste de listes suivante :

De cette liste, on extrait alors les listes dont le premier item est égal à 1.

Finalement, en mappant à la liste résultat la fonction item(last), on obtient la liste des antécédents de 1 dans la liste Y.

Nous devons maintenant appliquer un Keep pour obtenir tous les antécédents de 1 par la fonction Liste. [62]
Le script qui découle de ce raisonnement est donc celui-ci :
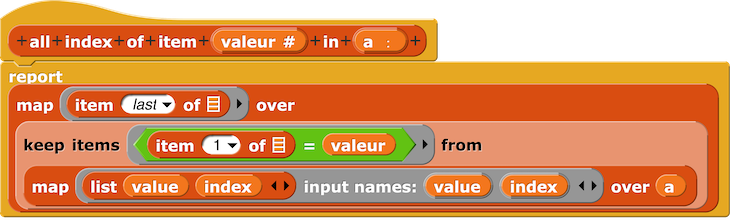
Et nous avons bien : Liste⁻¹(1) = {3, 4, 6, 7} [63]

– Traitons maintenant un autre exemple cette fois en Python.
Nous avons d’abord besoin d’une fonction qui construit une liste de nombres compris entre a et b [64] :
def numbers(a,b):
if (a > b):
return []
return [a] + numbers(a+1,b)ou
def numbers_(a,b):
if (a > b):
return []
return list(range(a,b+1))Dans la liste alpha = [3, 1, 2, 3, 4, 5, 3, 7, 3, 3], les index de la valeur 3 sont 0, 3, 6, 8 et 9 :
alpha = [3, 1, 2, 3, 4, 5, 3, 7, 3, 3]
numbers(0, len(alpha)-1) # renvoie la liste [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] qui contient les index de la liste alpha
c = map(lambda a,b: [a, b], alpha, numbers(0, len(alpha)-1))
# print(c) renvoie [[3, 0], [1, 1], [2, 2], [3, 3], [4, 4], [5, 5], [3, 6], [7, 7], [3, 8], [3, 9]]
d = filter(lambda x: x[0] == 3, list(c))
# print(d) renvoie [[3, 0], [3, 3], [3, 6], [3, 8], [3, 9]]Renverser une liste

Le script last at the top place le dernier élément d’une liste au début de la liste :

On renverse la liste avec un appel récursif à reverse(last_at_the_top) :

def last_at_the_top():
# à écrire ;-)
return()
def reverse(a):
if a == []:
return a
return [a[-1] + reverse(last_at_the_top(a)[1:])]Insérer un élément


def insert_(n,id,lst):
return lst[:id]+[n]+lst[id:]
lst = [1, 2, 3, 4]
insert_(99,3,lst)
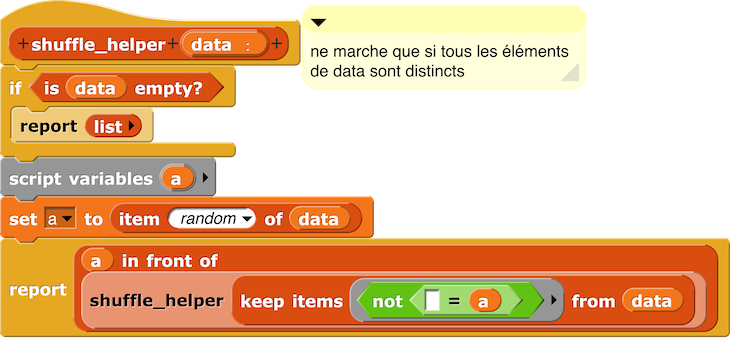
[1, 2, 3, 99, 4]Secouer les éléments d’une liste (shuffle)

Script Shuffle

Où le script Shuffle helper est :
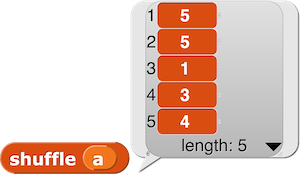
Si je secoue la liste [1,5,3,4,5], j’obtiens
Mélange des entiers de 1 à 7

Concaténation
Il s’agit de réécrire la fonction append(a, b) de Snap! qui concatène deux listes.
En Python, on pourra s’amuser à réécrire a + b pour deux listes a et b.
ToDo list
– échanger deux éléments
– tester si une sous-liste appartient à une liste
– ordonner une liste
Efficacité du trio Map/Filter/Reduce en programmation
Le trio Map/Filter/Reduce permet une parallélisation des processus pour des données massives.
– Utilisation par les développeurs professionnels
Julien Aymé est développeur Java travaillant dans la grande distribution à la Réunion. Je lui ai demandé de m’expliquer le rôle de Map-Reduce et son utilisation dans son développement.
Voici l’interview de Julien, développeur Java. [65]
En gros, il y dit qu’on effectue le découpage des paquets de données (streams) en plus petits paquets sur lesquels les algorithmes seront appliqués en parallèle, puis on regroupe les résultats. On y gagne en efficacité pour des gros paquets de données (streams). Voir une explication détaillée du fonctionnement de Map-Reduce sur Wikipedia. Par exemple, pour son utilité dans le cloud computing, il y est dit ceci :
Le MapReduce a émergé en 2004 comme un important modèle de programmation pour les applications utilisant d’énormes quantités de données grâce à sa répartition efficace du travail sur différents nœuds de calcul. Il commence notamment à être utilisé dans le Cloud Computing car son nombre de données stockées et manipulées ne cesse de croître. Il est donc nécessaire d’avoir un moyen d’améliorer le traitement des données au sein du Cloud.
Vous trouverez de nombreux sites expliquant l’utilisation de Map/Filter/Reduce en programmation. [66]
Notez qu’une librairie Streams (Lazy lists) est fournie avec Snap!.
Comment le présenter aux élèves en cours de mathématiques ?
Avec Snap!, on peut évidemment reformuler les titres des blocs Map, Keep, Combine afin qu’ils soient facilement utilisables par les élèves. J’ai donc reformulé le trio Map/Keep/Combine à des fins pédagogiques, afin que ces blocs soient plus accessibles aux élèves, comme ceci : Appliquer/Extraire/Combiner.
À propos de fins pédagogiques, remarquons tout d’abord que la team de Snap! a choisi de manière délibérée d’appeler ce trio Map/Keep/Combine au lieu de Map/Filter/Reduce afin que ces termes soient clairement compréhensibles par les jeunes codeurs, même si la plupart des langages utilisent Map/Filter/Reduce. En particulier, le mot filter ne distingue pas les filtres entrants [67] des filtres sortants [68]. Keep est totalement non ambigü, il désigne bien un filtre entrant. [69]
Le lutin Squelette du projet Snap! lié à cet article est consacré à cette présentation.
– Faire un Map, c’est simplement Appliquer une fonction à une liste de données. On obtient une liste transformée contenant le même nombre d’objets que la liste de départ.

– Faire un Keep (ou Filter), c’est Extraire des éléments d’une liste en appliquant un prédicat à cette liste de données (une condition est-elle vérifiée ou pas ?). On obtient alors une liste extraite de la liste de départ ; cette liste contient les éléments vérifiant la condition demandée.
Ainsi, le script suivant permet d’extraire les multiples de 7 des entiers non-nuls inférieurs à 50.

– Effectuer un Combine (ou un Reduce), c’est Combiner, appliquer à la liste de départ une fonction dont l’image est un objet unique, résultat d’une combinaison des éléments de la liste de départ. On pourra illustrer un exemple de Combine avec des nombres réels par le produit scalaire de deux vecteurs [70].

La somme des 10 premiers entiers est égale à 55. Tous les lycéens connaissent(aient...) ce résultat !
Effectuer un Combine (ou un Reduce), c’est donc appliquer un opérateur de E × E dans E aux éléments de E comme indiqué dans la note [13]. L’exemple le plus simple à mon sens est la somme des éléments d’une liste de nombre réels.
On pourra demander aux élèves de chercher des exemples avec des nombres (autre que le produit scalaire) mais aussi avec des objets d’autres types.
Dans cet exemple : Combine (liste[1:10] avec l’opérateur join( , ) ), nous allons obtenir 12345678910.

Cela permettra de réfléchir avec les élèves sur le sens d’un opérateur, essence de tous calculs...
– Appliquer/Extraire/Combiner (Map/Keep/Combine) avec quelques exemples concrets.
Appliquer/Extraire (Map/Filter ou Map/Keep)

On obtient la liste des cubes pairs inférieurs à 1000.
Appliquer/Combiner (Map/Reduce ou Map/Combine)

La somme des dix premiers cubes est égale à 3025.
La longueur d’une liste pourra s’obtenir en mappant la fonction constante x ↦ 1 à la liste : [71]

puis en combinant les valeurs 1 obtenues à l’aide de l’opérateur + .
En fait, la simple action de compter, c’est Combiner (Reduce).

— Dans un genre plus fun, on pourra travailler avec les élèves sur des lutins polygonaux.

polygone a 5 cote de cote 50
|
[72]

Pour obtenir une série de 2 triangles, un carré, un pentagone,
un hexagone et un heptagone, on pourra faire :

Et pour obtenir une liste de 3 triangles, 2 carrés, 3 pentagones, 3 hexagones et 2 heptagones :

On pourra ensuite combiner les lutins polygones obtenus avec l’opérateur créé à cet effet qui combine et tamponne deux lutins sur l’image :

D’où le résultat (avec parfois plusieurs tampons appliqués) :

Amas de polygones avec combine
|

Amas de polygones avec combine 2
|

Amas de polygones avec combine 4
|

Amas de polygones avec combine 5
|
Les élèves pourront ainsi s’amuser à créer des polygones étoilés.
Vous trouverez les scripts ci-dessus dans le lutin Polygones du projet Snap! lié à cet article.
Extraire/Combiner (Filter/Reduce ou Keep/Combine)

La somme des carrés d’entiers inférieurs à 100 est 385.

Le plus grand nombre premier inférieur à 100 est 97.
Appliquer/Extraire/Combiner (Map/Filter/Reduce ou Map/Keep/Combine)
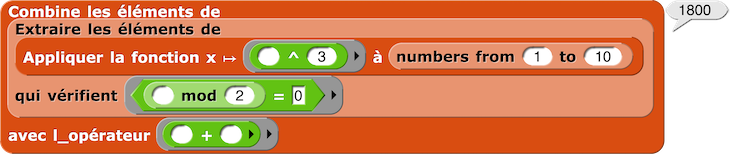
La somme des cubes pairs des 10 premiers entiers est 1800.
En appliquant le trio Appliquer/Extraire/Combiner (Map/Filter/Reduce ou Map/Keep/Combine) en classe, nous allons pouvoir mettre l’accent sur la notion de fonction, demander aux élèves quel est l’ensemble de départ, l’ensemble d’arrivée, réfléchir sur des notions profondes liées aux fonctions. Travailler sur le sens.
En classe, nous allons principalement travailler avec des nombres. Appliquer une fonction (donc utiliser le bloc Map) à une liste de nombres, c’est utiliser une suite de fonctions de référence. Par exemple, calculer $(1 + 1/x)^x$ , c’est appliquer la fonction inverse, ajouter 1, puis élever le résultat obtenu à la puissance $x$ (opérateur d’exponentiation).
Combiner une liste de nombres ne pourra se faire qu’avec des opérateurs associatifs. Les opérateurs les plus utilisés seront + , ×.
On pourra par exemple demander aux élèves de coder l’opérateur d’exponentiation ^ sans utiliser un algorithme récursif, ce qui peut être très instructif. Il suffit de se référer à la définition.
a ^ b = (a × a × ... × a) b fois.
Il suffit donc d’appliquer la fonction constante x ↦ a à une liste quelconque de b nombres entiers ;-), puis appliquer Combine avec l’opérateur × à la liste qui résulte du Map précédent.
On pourra revenir à la définition d’un opérateur avec les élèves et leur demander de coder les opérateurs min, et max.
Puis rechercher le minimum ou le maximum d’une liste en utilisant Combine et l’opérateur a min b ou a max b.
On travaille sur le fond des mathématiques.
Lorsque l’on commence à raisonner en termes de Appliquer/Extraire/Combiner (Map/Keep/Combine), on ne pense plus que comme cela. On ne revient plus jamais aux algorithmes de type séquentiels et on découvre des manières vraiment très élégantes de coder les algorithmes, ces manières étant du pur raisonnement fonctionnel, toujours !
Cela est parfois bien sûr très difficile mais cela en vaut le détour ! Plus nos élèves apprendront tôt à raisonner en ces termes, plus ce sera ancré dans leur mode de pensée : raisonner en fonctionnel ! Je suis intimement persuadée qu’en leur montrant ce raisonnement très tôt au collège, ils auront moins de mal que nous [73] par la suite à coder des algorithmes plus délicats.
Map/Keep/Combine expliqué aux élèves de NSI [74]
La récursivité est au coeur de la programmation fonctionnelle.
Map, Keep, Combine sont des fonctions d’ordre supérieur récursives. [75]
La multiplication dans Snap! comme opérateur d’ordre supérieur
Demandons donc aux élèves pour commencer de coder les opérateurs de base comme étant des opérateurs d’ordre supérieur, comme dans Snap!.

Si nous voulons coder cet opérateur en Python, passons par Snap! au préalable pour écrire ce script opérateur d’ordre supérieur multiplier x_ par y_ dans lequel x_ et y_ sont des listes :

Ainsi, la liste des entiers de 1 à 10 multipliée par la liste des entiers de 2 à 3 donne :

D’où le code Python : [76].
def multiplier(x_, y_):
if x_ == [] or y_ == []:
return []
return [x_[0]*y_[0]] + multiplier(x_[1:],y_[1:])multiplier([1,2,3,4],[2,4]) # renvoie [2, 8] Proposition de codage des blocs Map, Keep, Combine
On pourrait donc ensuite demander aux élèves de NSI de coder les blocs Map, Keep, Combine avec des fonctions récursives, à condition qu’ils soient déjà aguerris aux manipulations de listes. [77]
– La fonction Map
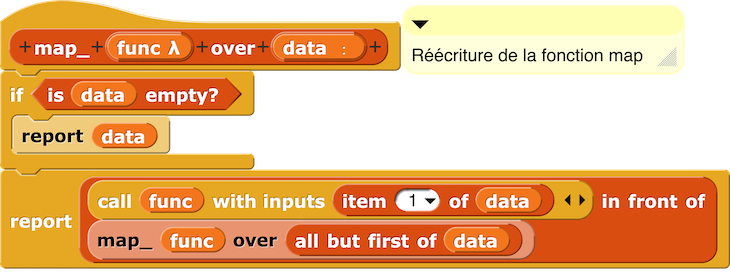
En Python, cela donne : [78]
def map_(func, data):
if data == []:
return data
return [func(data[0])] + map_(func,data[1:])map_(lambda x: x*x, [1,2,3,4,5]) # renvoie [1, 4, 9, 16, 25]– La fonction Keep

Code Python proposé pour redéfinir la fonction filter : [
Ce code est une traduction pure du code Snap!. Il est proposé sans garantie pour des listes de grande taille car le script renvoie alors RecursionError : maximum recursion depth exceeded in comparison car on dépasse la limite de 1000 itérations.
On peut connaître la limite de la profondeur de récursion autorisée par Python dans sa version 3.9.12 utilisée ici :
import sys
print(sys.getrecursionlimit())Il est malgré tout possible de repousser cette limite :
import sys
sys.setrecursionlimit(2000)Sinon, il faut revoir les conditions d’arrêt qui assurent que la fonction récursive arrive bien à se terminer avec un nombre d’appels récursifs imbriqués suffisamment raisonnables.
Mais je n’ai pas ce problème dans Snap!, avec les valeurs que j’ai testées.
On lira avec intérêt cet article [ [Solved] RecursionError : maximum recursion depth exceeded while calling a Python object
. ]].
def filter_(pred, data):
if data == []:
return data
if pred(data[0]):
return [data[0]] + filter_(pred,data[1:])
else:
return filter_(pred,data[1:])
filter_(lambda x: x % 2 == 0, [1,2,3,4,5]) # renvoie [2, 4]
filter_(lambda x: x % 2 == 0, entiers_1_a_n(100)) # renvoie les entiers pairs compris entre 1 et 100.– La fonction Combine
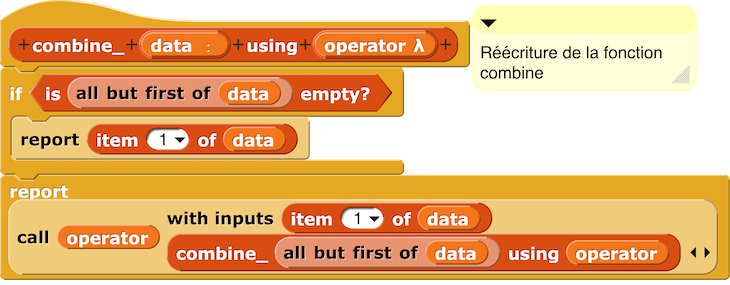
Code Python proposé pour Reduce :
def reduce_(operateur,data):
if data [1:] == []:
return data[0]
return operateur(data[0], reduce_(operateur,data[1:]))reduce_(lambda x,y: x+y, [1,2,3,4,5]) # renvoie 15Algorithmes de tri au programme de NSI : tri par insertion, tri par sélection
Les algorithmes de tri sont des exemples d’algorithmes qui font appel à deux notions profondes : ils font appel à la fois à la récursivité et aux fonctions d’ordre supérieur.
Algorithms explained and animated
|
Algorithmes de Tris
|
Je conseille à vos élèves l’excellente application Algorithms Explained and Animated sur téléphone du chercheur japonais Moriteru Ishida.
Ils y trouveront des animations très claires des algorithmes de tri suivants : Bubble sort, Selection Sort, Insertion Sort, Heap Sort, Merge Sort, Quicksort. D’autres nombreux algorithmes de Computer Science y sont aussi expliqués.
Les tris par sélection et par insertion ont été proposés dans les programmes de NSI de Première. Je vous propose ci-dessous des versions récursives de ces deux algorithmes de tri.
– Script Tri par sélection

– Script Tri par insertion
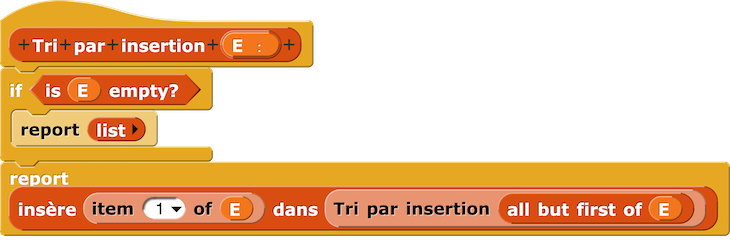
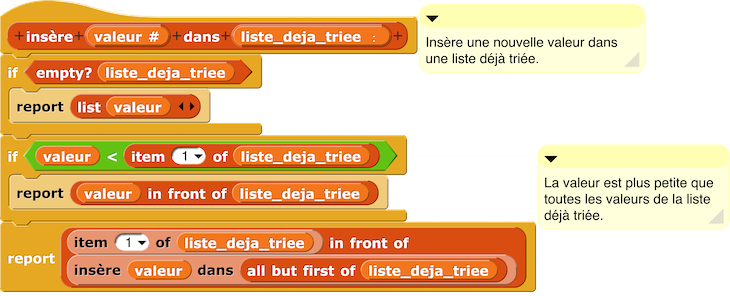
Où le script Insère valeur dans liste déjà triée est :
Si alpha est la liste [5,9,7,10,4,3,6,10,1,2], la liste triée donne :

Le tri fusion a été proposé dans les programmes de NSI de Terminale comme exemple d’algorithme de tris pour illustrer la méthode « diviser pour régner ». Ce tri fusion est un algorithme récursif qui se prête particulièrement aux listes chaînées.
Vous trouverez le tri fusion (merge) dans les algorithmes de tri proposés par Brian Harvey dans ce projet Snap!.
Le lutin Listes du projet Snap! lié à cet article est consacré aux algorithmes de Tri.
Conclusion
Pour terminer, je pense qu’il est très important de mettre les élèves dès le début du collège devant une programmation fonctionnelle visuelle grâce à Snap! utilisant le trio Map/Keep/Combine. En effet, persister à ne faire que de la programmation séquentielle avec les élèves risque de les enfermer dans un schéma de pensée dont ils auront un mal fou à se débarrasser.
Les façons de penser finissent par devenir des automatismes. Si vous avez l’habitude de programmer avec des boucles, il devient plus difficile de développer l’aptitude d’écrire des algorithmes en utilisant des fonctions d’ordre supérieur. Mais vos élèves n’ont pas encore cet automatisme d’utiliser des boucles, donc si vous leur enseignez les fonctions d’ordre supérieur très tôt, ils trouveront leur utilisation naturelle. [79]
Par ailleurs, si vous avez quelques élèves qui programment en Python depuis qu’ils ont 11 ans, ils risquent d’être surpris par vos méthodes et vous demander pourquoi vous ne codez pas des boucles comme tout le monde (itératif vs fonctionnel...). Dites-leur simplement que c’est à eux de décider s’ils sont prêts à apprendre quelque chose de nouveau dans votre classe ou s’ils veulent programmer à 30 ans de la même façon qu’à 11 ans. [80]
Je pense qu’il est important de comprendre que ce mode de programmation permis grâce à Map/Keep/Combine (Map/Filter/Reduce) est abordable avec des exemples simples très tôt dans un cursus d’apprentissage des algorithmes mathématiques.
Nous allons ainsi aider nos élèves à placer au centre des résolutions de problèmes l’essentiel en mathématique : la notion de fonction. Nous allons ainsi les aider à mieux comprendre l’essence des mathématiques, et à être moins bloqués par cet apprentissage.
Le mot de la fin.
Avez-vous remarqué qu’il n’y a pas une seule boucle dans les scripts de cet article ? ...
PostScriptum
* Le lecteur vigilant aura certainement pris note du mélange de l’anglais et du français dans l’écriture des scripts. Lorsque je code, je raisonne en fait dans les deux langues et vous livre ici le résultat de mes réflexions. L’uniformisation de tous les scripts serait un travail à finaliser même s’il n’est pas essentiel.
De nombreuses langues sont supportées dans Snap!. Si la vôtre n’y est pas, ou si les traductions de certains scripts viennent à manquer, il est possible de contribuer au projet Snap! sur Github et d’y proposer une traduction.
* Pour information aux lecteurs, tout ce qui est contenu dans cet article est délivré sous licence Creative Commons BY-NC-SA [81]. Cette licence s’applique également aux projets Snap! vers lesquels cet article pointe.
Remerciements
Je remercie chaleureusement :
* Brian Harvey passionné, comme Seymour Papert de l’éducation Mathématique des enfants par les ordinateurs, enseignant en Computer Science [82] pour ses critiques sans complaisance sur le fond du sujet.
* Mon ami Yves Martin pour ses conseils avisés tant sur le fond que sur la forme de cet article. Avec Yves, nous faisions partie de l’association AbraCAdaBRI comprenant 5 félés du logiciel Cabri et Géomètre, un des premiers logiciels de géométrie dynamique. Cette association avait été créée par Éric Hakhenholz dans le but de publier la revue AbraCAdaBRI papier diffusée à environ 200 exemplaires pendant 2 ans. Cette revue papier fut une aventure extraordinaire. Éric a eu la bonne idée de la remettre en ligne sur dgpad.net. [83]
Spéciale dédicace
Je dédie ce travail à mes enfants et petits-enfants. Mais bien évidemment aussi à Mes Élèves et à tous ceux que je n’aurai pas.
Annexe
Vous trouverez dans cet article une annexe de géométrie. Elle existe pour montrer à quel point adopter une structure de données appropriée pour la mise en oeuvre d’un algorithme est aussi important que l’algorithme lui-même.
Table des matières
- Premier tour d’horizon avec Map/Keep/Combine ou Map/Filter/Reduce
- Premiers exemples d’application de fonctions à une liste d’objets avec Map
- Tableau de valeurs d’une fonction
- Obtenir une liste aléatoire de booléens
- Calcul de la puissance n-ième d’une matrice (sans récursivité)
- Appliquer le négatif à un rectangle de pixels colorés
- Exemples de réduction avec Combine
- Somme
- Produit
- Moyenne arithmétique
- Moyenne géométrique
- Moyenne harmonique
- Produit scalaire
- Exemples d’extractions avec Keep
- Qu’est-ce qu’un prédicat ?
- Ce nombre est-il positif ?
- Ce nombre est-il pair ?
- Ce nombre est-il premier ?
- Ce nombre est-il un carré ?
- Ce nombre est-il un cube ?
- Exemples concrets d’extractions avec Keep
- Extraire les nombres positifs d’une liste de nombres
- Extraire les nombres pairs d’une liste de nombres
- Extraire un ensemble de carrés
- Extraire les entiers d’un ensemble de nombres
- Obtenir les classes d’équivalence modulo n
- La notion de Fonction au centre de l’apprentissage des Mathématiques
- La puissance des listes conjuguée à une pensée fonctionnelle
- De la décomposition canonique d’une application à une décomposition de type Map/Filter/Reduce
- Exemples progressifs niveau lycée
- Second degré
- Combinaisons de k éléments d’un ensemble à n éléments
- Somme des (k parmi n) = 2ⁿ
- Maximum, minimum, quartiles, médiane
- ToDo list
- Un peu d’arithmétique
- Diviseurs de n
- Nombres premiers, Crible d’Ératosthène
- Fonction Phi d’Euler
- Test de primalité de Fermat
- ToDo list
- Calculs sur les suites
- Somme, produit, suite de Fibonacci, suite de Syracuse
- Somme des termes d’une suite
- Produit des termes d’une suite
- Suite de Fibonacci
- Suite de Syracuse
- Suite ((1 + 1/n )ⁿ)
- Applications : Recherche de valeurs approchées
- Constante d’Apéry
- Encadrement de e
- Approximation de π par Ramanujan
- ToDo List
- Et en géométrie ?
- Le problème de Fermat
- Barycentre d’une liste de points
- Transformations géométriques
- Courbes algébriques
- Variations autour de la lemniscate de Bernouilli
- ToDo List
- De l’intérêt du Map/Keep/Combine
- Travail sur les listes
- Tous les index d’un item dans une liste
- Renverser une liste
- Insérer un élément
- Secouer les éléments d’une liste (shuffle)
- Concaténation
- ToDo list
- Efficacité du trio Map/Filter/Reduce en programmation
- Comment le présenter aux élèves en cours de mathématiques ?
- Appliquer/Extraire/Combiner
- Appliquer/Extraire (Map/Filter ou Map/Keep)
- Appliquer/Combiner (Map/Reduce ou Map/Combine)
- Extraire/Combiner (Filter/Reduce ou Keep/Combine)
- Mixer Appliquer/Extraire/Combiner (Map/Filter/Reduce ou Map/Keep/Combine)
- Map/Keep/Combine expliqué aux élèves de NSI
- La multiplication dans Snap! comme opérateur d’ordre supérieur
- Proposition de codage des blocs Map, Keep, Combine
- Algorithmes de tri au programme de NSI : tri par insertion, tri par sélection, mais d’autres encore
- Annexe
- Annexe de géométrie
- Le problème de Fermat
- PostScriptum
- Remerciements
Cet article a été coédité avec le site MathémaTICE de la revue Sesamath, sur lequel il a été publié sous le titre Le trio Map/Filter/Reduce au coeur de la notion de fonction. [84]





















Commentaires